Beauty of Probability

In a recent trip with the family.....yes I sneak off to play craps nearby. Funny how we always have one not far away? I noticed another fascinating thing that my better half just doesn't find that interesting.
There are math gurus who monitor this site like MathExtremist and they are just what I need so here's the question...
What are the odds of rolling multiple 7's without one 6 or one 8?
Ie...
A 7 is 6 in 36
A 6 or an 8 is 10 in 36....after that I'm mathematically handicapped!
How 'bout 2 7's before a 6or8?
3 7's before a 6or8?
4 7's before a 6or8?
5 7's before a 6or8?
6 7's before a 6or8?
7 7's before a 6or8?

Thanks for any help with this quandary!!!!!

http://stattrek.com/online-calculator/binomial.aspx

i imagine its .375 (6/16) ^ x ?

prob win (a 7) .375 .. 3 trials with 3 wins .0527 (1 in 18.96)
ect

could be wrong just going by what i have seen sally post in the past-- at least what I understood :)

bahdbwoy
Thanks for your post on this, one of the things that most players have a hard time understanding is problems like this. That is why I say we always need the math guys! When you are trying to figure out some of these claims to fame like rolling 18 fours and 19 tens in one roll.

Quote:

As I mentioned above, all 13 PL-Points only encompassed three numbers (the 4, the 6, and the 10). For me, that in itself was a pretty high accomplishment that is rare as can be. I’ve thrown 13-Pointers before; but never were they restricted to just three different box-numbers.

After reading the about quote some of us did the math, with what information the poster had posted and it worked out to something like he rolled 18 fours and 19 tens in one roll. Then we did the math by asking here on the Wizards board what the probability of rolling that many 4’s and 10’s in one roll would be. The numbers the guys came up with were astronomical!

I’m going to start posting this calculator when we read some of these outlandish claims to fame!

Quote:

bahdbwoy
http://stattrek.com/online-calculator/binomial.aspx

i imagine its .375 (6/16) ^ x ?

prob win (a 7) .375 .. 3 trials with 3 wins .0527 (1 in 18.96)
ect

could be wrong just going by what i have seen sally post in the past-- at least what I understood :)

removed
silly

Sally

Hey MS Sally, I want to b make sure I read that right. For example the chart shows that to roll 3 7's without rolling a 6 or an 8 would be 1 in 18.96 rolls or also 5%???
Did I read that right? Thanks for your insight and response

I have to ask aka: just what does this kind of info do for you, and will it change how you play at the casino? I get how sets and sets of stats make a certain segment excited. But is any of it useful enough that you could expect to perform better in a casino? Thanks.

removed
silly

Sally

The numbers are fascinating. As I'm sure you're more deeply versed in the "stats", I don't fall into any "segment"
I have no idea if it would help me the next time I play or not? I play sparingly so while I appreciate your curiosity, did I understand the chart correctly?
Thanks!

WOW! Thank you for the breakdown! It's incredible! You are amazing. I greatly appreciate your time and attention on this!
Thanks MS Sally (I'm being presumptuous on the MS so if I'm not correct, forgive me)

the thing I never was really clear on is if you take a series of dont pass vs pass results and looking for 3 passes in a row how do you determine the start/end of a trial?

pass / dont pass --- is that trial over or do you still complete the set of 3
pass / pass / dont / dont / pass / dont -- how many trials is that? 3

Quote: akarags

WOW! Thank you for the breakdown!

Thank you for the question.
Because you asked about the number of rolls needed I can easily solve this in Excel using a Markov chain approach too.
I have done this before for the distribution.
Here is the table for that. The first 200 rolls.
This is only for the 3 7s in a row before the 6 or 8
0.503060653 = 46 rolls. that would be the over/under
The roll that has the highest probability of being the 3rd in a row 7 looks to be the 9th roll by a tiny tiny margin.

Sally

Huh? That's not what I was wagering?
You may have been on a different thread...

So Sally, does the fact that the combined probability that the 6 carries a 5 of 36 chance and the 8 carries the same better the odds on any given roll to 10 of 36 versus the 7's 6 of 36? Am I getting that wrong? Does that not affect the chance or is that part of your computation?
And you must be the next Wizard!!!

Quote: tournamentking

I have to ask aka: just what does this kind of info do for you, and will it change how you play at the casino? I get how sets and sets of stats make a certain segment excited. But is any of it useful enough that you could expect to perform better in a casino? Thanks.

For me it helps to put things into perspective. I leave a craps table thinking how is it possible that I got killed by such a long shot? One example: on the DP/DC with three fours in a row? Get home and crunch the numbers and find that, after the DP + odds is on the 4 and I have a DC bet, shooter hits the 4, not any other number or 7 (3/30). Now with the DC + odds on the 4 and a DP bet, shooter rolls another 4 (3/30). So there are my 3 dark side bets for that roll, but all I have to show for it is one bet on the 4, and now I wait ... and eventually the shooter hits the 4 again (3/9). It's not 1 in a million, which it felt like at the time, but 1 in 300. That's likely enough that I realized I'll see it more than a few times in my lifetime.

Quote:

seattledice
For me it helps to put things into perspective. I leave a craps table thinking how is it possible that I got killed by such a long shot? One example: on the DP/DC with three fours in a row? Get home and crunch the numbers and find that, after the DP + odds is on the 4 and I have a DC bet, shooter hits the 4, not any other number or 7 (3/30). Now with the DC + odds on the 4 and a DP bet, shooter rolls another 4 (3/30). So there are my 3 dark side bets for that roll, but all I have to show for it is one bet on the 4, and now I wait ... and eventually the shooter hits the 4 again (3/9). It's not 1 in a million, which it felt like at the time, but 1 in 300. That's likely enough that I realized I'll see it more than a few times in my lifetime.

It’s not uncommon to see a bunch of 4’s and 10’s being rolled any more, here in Vegas. The DP/DC guys will get killed when they are betting them. You have to check out the tables anymore to see what the trend of the table is doing, there are times when nobody is throwing the 6’s and 8’s and everybody is throwing the outside numbers!

You are constantly seeing guys that lay the outside points getting picked off, and when those outside numbers are being rolled, the players are still sticking to what they have learned from all the books and of course the helpful dealers, and that is to only bet on the 6’s and 8’s!

You need to know the math of the game, but you also need good old common sense when playing craps, bet on what is being rolled! We see a lot of strange things on craps tables and it’s always very interesting to figure out what they odds of something happening are!

The one thing I love about this site is you have guys like the Wizard and let’s not forget Mustangsally that are willing to do and show you the math and how they arrived at the answer to your questions. Mustangsally has answered a few of my questions on some of the outlandish claims to fame that I’ve read on different craps boards. When you see the odds of some of these claims happening it, shocking what the odds really are of happening!

I truly appreciate all the hard work any of you math guys put into answering any of our questions! If I left you out, the only reason is I’ve not seen enough of your work, and the fact that it’s hell getting old you can’t remember anybody’s name!

...

deleted

removed
silly
Sally

Quote: Ibeatyouraces

Trending doesn't work, period! Doesn't matter if its craps or baccarat. If it did, I'd be doing it which I don't.

While I agree the past roll does not predict the next roll or two, I see no harm in betting on whats being thrown right now. Im with superrick on this one. Hell, even Dicesitter said this in a post a few mos. back and altho I dont believe a thing he says about dc I do believe he is right about betting on whats being thrown. Hey, lets not leave 7craps out when we are talking about the math guys on this site.

Sally, I had my terminologies wrong...sorry. I did have an uncanny bit of good luck with the 6's and 8's. I quit after a half hour but using presses was able to make quite a bit on a very small bankroll. While I know that the game will turn it was interesting to see how it ran like it did. Thanks!
I wonder how a progression might work off an initial 7 out? Your insight is staggeringly informative, wow! I'll spen some time absorbing the chart and am sure I'll have other questions if you're available to help?!

deleted

I missed your post at first

Quote: bahdbwoy

the thing I never was really clear on is if you take a series of dont pass vs pass results and looking for 3 passes in a row how do you determine the start/end of a trial?

a trial or an attempt is to try for an event - in your case 3 in a row pass line wins ends the trial but so does a pass line loss any time before 3 wins in a row.

Quote: bahdbwoy

pass / dont pass --- is that trial over or do you still complete the set of 3

yes, the trial is over. it's length was 2 and was not successful
the only set of 3 you are trying to complete is 3 pass wins in a row

Quote: bahdbwoy

pass / pass / dont / dont / pass / dont -- how many trials is that? 3

yes
pass / pass / dont <<< almost 3 in a row
dont
pass / dont
all 3 trials - or attempts - at 3 in a row wins failed.

Sally asks
How many pass line bets does one have to make on average to see 3 pass line wins in a row?

Here is the long way

A simple method and there are a few formulas for this

for the distribution of a streak of length 3
one should use a calculator or a spreadsheet. makes the math very easy to complete.
I linked to one in an earlier post

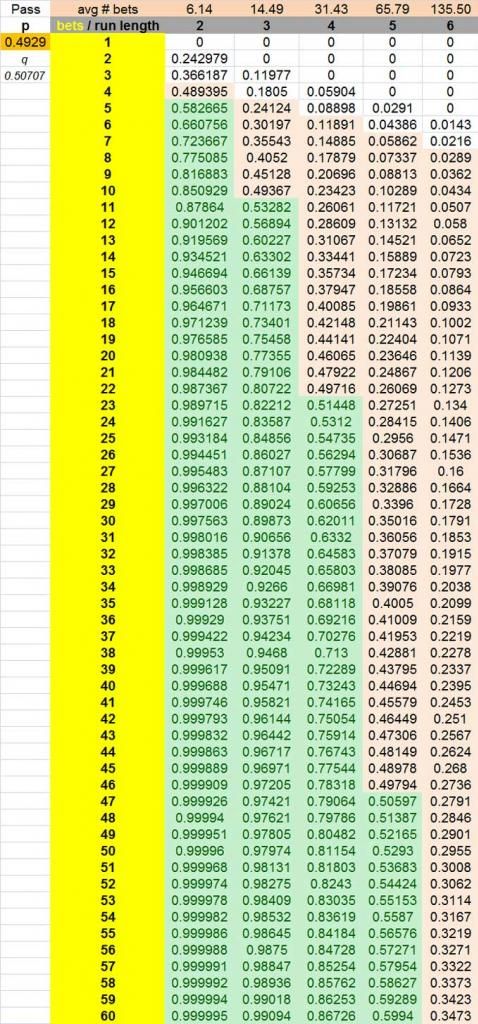
Sally

Gosh man, what a cynical lil dude. Just let "those" just do their thing. Take a page from Sally and be receptive or don't post. The negativity is not healthy! Happy holidays!!!

thanks for responding Sally, now I am clear on that moving forward..

So if I said how many dont pass bets resolved before 2 in a row that would be:

(1-.4793^2) / (.4929*.4793^2)

for 6.80252 and average of 23.60476 rolls?

Hey Sally love the video...so after a 7-out the dice are given to the next shooter to pick 2. They could be the same, one could be different or both could be different...how is this accounted for? Or does it not matter? As always, thanks...

removed
silly

Sally

this is probably completely wrong and probably not asking correctly but..

Is that saying on bet 10 if there has not been a streak of 2 and bet 9 won there is a .1587 chance that bet 10 would fail to complete a streak of 2 (ignoring any pushes in between). I know that individual bet still has normal probability of winning..
So 1 in 6.30 times you get to a 10th bet before you saw 2 in a row you would fail at winning the 9th/10th bet?

or simply a .0350 chance that a streak of 2 wont complete until the 10th bet?

Quote: bahdbwoy

Is that saying on bet 10 if there has not been a streak of 2 and bet 9 won there is a .1587 chance that bet 10 would fail to complete a streak of 2 (ignoring any pushes in between).

To explain the distribution table.
Each row probabilities are to be in one of the 3 states (0 win, 1 in a row and 2 in a row) after a bet is resolved.

So yes after the 10th bet is resolved, there would be a 0.1587 chance of not hitting a 2 in a row win
0.09886143 would be the chance of having 0 wins in a row
0.059868517 would be the chance of having 1 win in a row

I like the .711 probability of hitting 2 in a row by the 7th bet.
Maybe the don't pass player likes it too.

Quote: bahdbwoy

I know that individual bet still has normal probability of winning..
So 1 in 6.30 times you get to a 10th bet before you saw 2 in a row you would fail at winning the 9th/10th bet?

The 6.31 is just the average of doing this experiment many many times.
0.647650494 is the probability of seeing 2 in a row by the 6th bet resolved

Quote: bahdbwoy

or simply a .0350 chance that a streak of 2 wont complete until the 10th bet?

.0350 is the probability of the first 2 in a row wins happening on exactly the 10th bet resolved.

Sally

Anybody???

"Hey Sally love the video...so after a 7-out the dice are given to the next shooter to pick 2. They could be the same, one could be different or both could be different...how is this accounted for? Or does it not matter? As always, thanks..."

The probabilities of a shooter drawing dice according to the last shooter -

Both the same:
2/5 * 1/4 = 2/20 = 10%

Both different:
3/5 * 2/4 = 6/20 = 30%

That leaves the only other possibility - one the same, one different:
60%

You could also calculate it as:
-First one the same, second one different
2/5 * 3/4 = 6/20
PLUS
-First one different, second one the same
3/5 * 2/4 = 6/20

12/20 = 60%


But these have nothing to do with the probabilities of certain numbers appearing/not appearing before others.

Quote: wudged

The probabilities of a shooter drawing dice according to the last shooter -

Both the same:
2/5 * 1/4 = 2/20 = 10%

Both different:
3/5 * 2/4 = 6/20 = 30%

That leaves the only other possibility - one the same, one different:
60%

You could also calculate it as:
-First one the same, second one different
2/5 * 3/4 = 6/20
PLUS
-First one different, second one the same
3/5 * 2/4 = 6/20

12/20 = 60%


But these have nothing to do with the probabilities of certain numbers appearing/not appearing before others.

Thanks for the response...the question was pertaining to the following...
"Quote: akarags
So Sally, does the fact that the combined probability that the 6 carries a 5 of 36 chance and the 8 carries the same better the odds on any given roll to 10 of 36 versus the 7's 6 of 36? Am I getting that wrong? Does that not affect the chance or is that part of your computation?
And you must be the next Wizard!!!
It only makes a difference if you want to see "per decision" (only 6,7,8) or per roll. My last post was per roll based.

Now it would seem to me that the Craps players that make the place 6 and place 8 bets at the same time
feel they should really be winning more than they actually do.
Bad dice, poor shooters and all that goes with losing when not knowing what to expect and how bad it can be or good it can be.

Here is my table of the number of 6s and 8s before a 7. The number of hits.

37.5% or about 38 out of 100 attempts on average results in 0 wins, both bets lose. That looks to be about 76 units down just from that event.

How often should one get just one # then 7 out? 0 or 1 6 or 8 hit before the 7 out is about 61% or 61 out of 100 on average. sure looks like an uphill climb to me.

of course 39 out of 100 attempts at this betting method, the player is expected to get at least 2 hits the longer they play.
Now we are talking.
But it still does not look all that good trying to play catch up, to me.

also, it could be great.
about 1 in 110 attempts on average would hit 10 6s and 8s, at least, before the 7 out.
1 in 110 holds at least 2 times to hit 10 in a row 25% of the time. So it can really get good.
even the 1 in a Million is still attainable by someone. (retire after 29 6s and 8s before the 7 out)

One fact remains and should be understood
one is more likely to get 0 or 1 hits placing the 6 & the 8 before the 7out than any other number of hits.
Hope the trend is your friend when place betting.

# of times hit at least # 1 in (# of attempts) # or less # of times hit Exact # of hits 1 in (# of attempts)
0 100.00% 1.00 37.500000% 0 37.500000% 2.67
1 62.500000% 1.60 60.937500% 1 23.437500% 4.27
2 39.062500% 2.56 75.585938% 2 14.648438% 6.83
3 24.414063% 4.10 84.741211% 3 9.155273% 10.92
4 15.258789% 6.55 90.463257% 4 5.722046% 17.48
5 9.536743% 10.49 94.039536% 5 3.576279% 27.96
6 5.960464% 16.78 96.274710% 6 2.235174% 44.74
7 3.725290% 26.84 97.671694% 7 1.396984% 71.58
8 2.328306% 42.95 98.544808% 8 0.873115% 114.53
9 1.455192% 68.72 99.090505% 9 0.545697% 183.25
10 0.909495% 109.95 99.431566% 10 0.341061% 293.20
11 0.568434% 175.92 99.644729% 11 0.213163% 469.12
12 0.355271% 281.47 99.777955% 12 0.133227% 750.60
13 0.222045% 450.36 99.861222% 13 0.083267% 1,200.96
14 0.138778% 720.58 99.913264% 14 0.052042% 1,921.54
15 0.086736% 1,152.92 99.945790% 15 0.032526% 3,074.46
16 0.054210% 1,844.67 99.966119% 16 0.020329% 4,919.13
17 0.033881% 2,951.48 99.978824% 17 0.012705% 7,870.61
18 0.021176% 4,722.37 99.986765% 18 0.007941% 12,592.98
19 0.013235% 7,555.79 99.991728% 19 0.004963% 20,148.76
20 0.008272% 12,089.26 99.994830% 20 0.003102% 32,238.02
21 0.005170% 19,342.81 99.996769% 21 0.001939% 51,580.83
22 0.003231% 30,948.50 99.997981% 22 0.001212% 82,529.34
23 0.002019% 49,517.60 99.998738% 23 0.000757% 132,046.94
24 0.001262% 79,228.16 99.999211% 24 0.000473% 211,275.10
25 0.000789% 126,765.06 99.999507% 25 0.000296% 338,040.16
26 0.000493% 202,824.10 99.999692% 26 0.000185% 540,864.26
27 0.000308% 324,518.55 99.999807% 27 0.000116% 865,382.81
28 0.000193% 519,229.69 99.999880% 28 0.000072% 1,384,612.50
29 0.000120% 830,767.50 99.999925% 29 0.000045% 2,215,379.99
30 0.000075% 1,329,228.00 100.000000% 30 0.000028% 3,544,607.99
Sally
I Heart Vi Hart

Amy thoughts, Wudged, on how the changing of the dice affect any of this, if at all?

Assuming the dice are fair/unbiased and otherwise equal to each other, changing the dice has no effect at all. Each face on each die still has the same 1/6 probability of occurring.

If anyone is interested in the formula for the expected number of attempts (e.g. rolls) for a particular event to occur N consecutive times before another event takes place, the formula is:

Quote: mustangsally

I like the .711 probability of hitting 2 in a row by the 7th bet.
Maybe the don't pass player likes it too.

Sally

why do you like it?

if i said what is the probability that you would not have 2 DP winners in a row (exclusing push) is that p= 1-(.4929^2) ?

if so then is the probability of not getting a streak of 2 in 7 attempts p^7 = .142518 ?

thank you

Quote: bahdbwoy

if i said what is the probability that you would not have 2 DP winners in a row (exclusing push) is that p= 1-(.4929^2) ?

here is what I get.
yes, and that would be for just the very first 2 bets made (actually resolved)
=1 - (949/1925)^2 = 0.7569638

Quote: bahdbwoy

if so then is the probability of not getting a streak of 2 in 7 attempts p^7 = .142518 ?

not quite.
0.276245216

we have to calculate this at each step (each bet made) for the Run of 2 then subtract from 1.
look at the below table
almost twice as high of a probability of *no run of 2* in 7 resolved bets

# bets	at least 1 run of length 2	no run 2
1	0	1
2	0.243036195	0.756963805
3	0.366258702	0.633741298
4	0.489481209	0.510518791
5	0.582756187	0.417243813
6	0.660847379	0.339152621
7	0.723754784	0.276245216
8	0.775168613	0.224831387
9	0.816959849	0.183040151
10	0.850999477	0.149000523
11	0.878703764	0.121296236
12	0.901258431	0.098741569
13	0.919618649	0.080381351
14	0.934565075	0.065434925
15	0.946732259	0.053267741
16	0.95663705	0.04336295
17	0.964700106	0.035299894
18	0.97126389	0.02873611
19	0.976607182	0.023392818
20	0.980956923	0.019043077
21	0.984497859	0.015502141
22	0.98738038	0.01261962
23	0.989726916	0.010273084
24	0.991637129	0.008362871
25	0.99319215	0.00680785
26	0.994458025	0.005541975
27	0.995488519	0.004511481
28	0.996327399	0.003672601
29	0.997010295	0.002989705
30	0.997566211	0.002433789

I can break the table down like so (for column 2)
p = 949/1925
q = 1-p
run = 2

for bet #2 = p^run (0.243036195)
for bet #3 = Pbet#2+ (q*p^run) = 0.123222507 = 0.366258702

Now we have to look back to see if the Run of 2 did not happen earlier
and add that in
for bet #4 = Pbet#3+(1-Pbet#1)*q*p^run
for bet #5 = Pbet#4+(1-Pbet#2)*q*p^run
and so on down to complete the column in the table

runs or streaks are sneaky critters
but can be easily figured out using the right math
(and verified with simulation)
Good Luck