BJ House Edge in various conditions

8D, S17, NoSurr, NoDAS, DOA, PEEK on Ace, SPL1, SPLA1, Penetration = 50%, Flat Bet.

1) Flat Bet, Basic Strategy HE = -0.708%
2) Flat Bet, Hi-Opt 2 Counting Strategy(Full Index) HE = -0.588%
3) Flat Bet, Perfect Composition Dependent Strategy HE = ?

Anyone can help ? Thanks.

I would like to do an experiment on a 6-deck stand-17 with a cut card at 4.5/6 deck tomorrow. However, even with computer-perfect play at every decision point, your game probably is still negative HE.

Quote: aceside

I would like to do an experiment on a 6-deck stand-17 with a cut card at 4.5/6 deck tomorrow. However, even with computer-perfect play at every decision point, your game probably is still negative HE.
link to original post

You are not answering my question, it does not matter negative/positive.

What is the HE for computer-perfect play ?

The answer depends on the specific rules.

Quote: aceside

The answer depends on the specific rules.
link to original post

I already given the rules.

8D, S17, NoSurr, NoDAS, DOA, PEEK on Ace, SPL1, SPLA1, Penetration = 50%, Flat Bet.

No Insurance, BJ 3 : 2, Split AA only draw 1 card . . . . .

Please let me know if you want any other rules.

I can only estimate. I guess nobody has ever tried this calculation.

Quote: aceside

I can only estimate. I guess nobody has ever tried this calculation.
link to original post

So what is the estimated HE ? What is your basis ?

Let me do my experiment first and then report you my results. Have fun!

Quote: aceside

Let me do my experiment first and then report you my results. Have fun!
link to original post

If possible, please use my exact BJ rules to do your experiment. Thanks

The answer depends on how many hands are in play and which seat you are in. At a full table, third base gets to see more cards after the cut card. This extra penetration is the most valuable in terms of computer perfect play.

Is it okay to assume heads up playing one hand?

Quote: Mental

The answer depends on how many hands are in play and which seat you are in. At a full table, third base gets to see more cards after the cut card. This extra penetration is the most valuable in terms of computer perfect play.

Is it okay to assume heads up playing one hand?
link to original post

heads up playing one hand

Quote: ssho88

8D, S17, NoSurr, NoDAS, DOA, PEEK on Ace, SPL1, SPLA1, Penetration = 50%, Flat Bet.

1) Flat Bet, Basic Strategy HE = -0.708%
2) Flat Bet, Hi-Opt 2 Counting Strategy(Full Index) HE = -0.588%
3) Flat Bet, Perfect Composition Dependent Strategy HE = ?

Anyone can help ? Thanks.
link to original post

I am assuming that Perfect Composition Dependent Strategy means computer perfect play using all information about cards that have been seen on this hand and prior hands. I ask because CDS usually just means a basic strategy based on the composition of the current player's hand. But OP's use of the word 'perfect' leads me to believe this is his assumption.

I made a table of the EV for an 8-deck game with all the cards of one rank depleted. In the table below, the first EV is always the same because no card has been removed for that rank. The last entry on the right is for all cards of that rank removed. For tens, I remove four cards per column to keep the row width the same. There are 34 columns. Use the slider to see the right edge of the table.

8 decks, S17, DOA, NDAS, SPL1, CDP

A	-0.57	-0.64	-0.72	-0.79	-0.87	-0.94	-1.02	-1.09	-1.17	-1.25	-1.33	-1.40	-1.48	-1.56	-1.64	-1.72	-1.80	-1.89	-1.97	-2.05	-2.14	-2.22	-2.31	-2.39	-2.48	-2.57	-2.65	-2.74	-2.82	-2.91	-3.00	-3.08	-3.17
2	-0.57	-0.52	-0.48	-0.43	-0.38	-0.33	-0.29	-0.24	-0.19	-0.14	-0.09	-0.04	0.01	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	0.60	0.65	0.70	0.76	0.81	0.86	0.92	0.97	1.03
3	-0.57	-0.52	-0.46	-0.41	-0.35	-0.29	-0.23	-0.18	-0.12	-0.06	0.00	0.06	0.12	0.18	0.24	0.31	0.37	0.43	0.50	0.56	0.63	0.70	0.78	0.85	0.92	1.00	1.07	1.15	1.23	1.32	1.40	1.49	1.57
4	-0.57	-0.50	-0.43	-0.35	-0.27	-0.20	-0.12	-0.05	0.03	0.11	0.18	0.26	0.34	0.41	0.49	0.57	0.65	0.73	0.81	0.90	0.98	1.07	1.15	1.24	1.32	1.41	1.49	1.58	1.68	1.77	1.87	1.97	2.08
5	-0.57	-0.48	-0.38	-0.29	-0.19	-0.09	0.01	0.11	0.21	0.31	0.41	0.51	0.62	0.72	0.83	0.93	1.04	1.15	1.26	1.38	1.50	1.61	1.73	1.85	1.97	2.09	2.22	2.35	2.48	2.62	2.75	2.89	3.02
6	-0.57	-0.52	-0.46	-0.41	-0.35	-0.29	-0.24	-0.18	-0.12	-0.06	0.00	0.06	0.12	0.18	0.25	0.32	0.39	0.46	0.54	0.61	0.69	0.76	0.84	0.92	1.00	1.08	1.16	1.24	1.33	1.42	1.51	1.61	1.70
7	-0.57	-0.54	-0.50	-0.47	-0.43	-0.40	-0.36	-0.32	-0.28	-0.24	-0.20	-0.16	-0.12	-0.08	-0.03	0.03	0.09	0.16	0.23	0.30	0.37	0.44	0.51	0.59	0.66	0.73	0.81	0.90	0.99	1.08	1.18	1.27	1.37
8	-0.57	-0.57	-0.58	-0.58	-0.58	-0.58	-0.58	-0.58	-0.58	-0.58	-0.58	-0.57	-0.57	-0.57	-0.56	-0.56	-0.55	-0.55	-0.54	-0.53	-0.53	-0.52	-0.51	-0.50	-0.49	-0.48	-0.47	-0.45	-0.42	-0.39	-0.37	-0.34	-0.31
9	-0.57	-0.60	-0.62	-0.64	-0.67	-0.69	-0.71	-0.74	-0.76	-0.78	-0.80	-0.82	-0.85	-0.87	-0.88	-0.90	-0.92	-0.93	-0.95	-0.96	-0.98	-0.99	-1.01	-1.02	-1.03	-1.05	-1.06	-1.07	-1.08	-1.09	-1.10	-1.10	-1.11
T	-0.57	-0.82	-1.06	-1.29	-1.53	-1.77	-2.00	-2.21	-2.41	-2.61	-2.78	-2.94	-3.07	-3.19	-3.28	-3.33	-3.32	-3.28	-3.20	-3.07	-2.87	-2.66	-2.42	-2.18	-1.91	-1.63	-1.31	-0.96	-0.57	-0.11	0.47	1.14	1.86

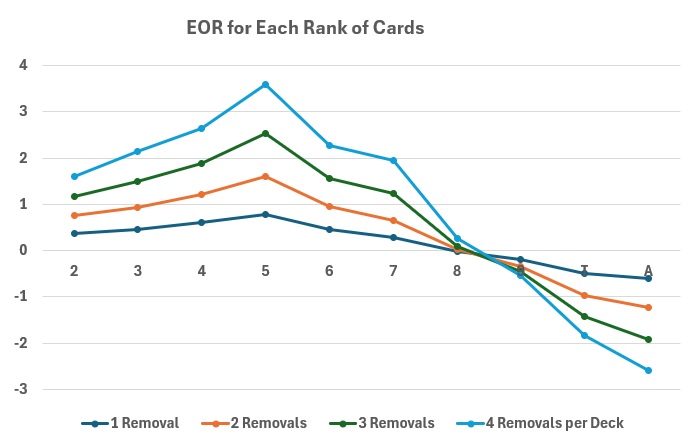
Of course, removing aces and tens affects the EV the most. When all of the tens are removed, I am seeing that the EV tilts towards the player again. I am not sure why this happens. I hope my calculations are correct. Can anyone confirm this?

On a typical shoe, all ranks deplete more or less evenly. You gain EV as you go through the shoe simply because there are fewer decks in the shoe. You gain more EV if some of the ranks are more depleted in that particular shoe and you can make strategy changes based on this information.

Card counters gain most of their EV by spreading their bet. I am not sure there is much EV gain simply from strategy changes when you force the player to flat bet. I intend to do some MC sims to answer this question. I won't do the EV for 50% penetration. Instead, I will look at the average and variance of the EV for a hand played after a given fraction of the shoe has already been exposed in prior play. This will create an EV vs. penetration curve. I am not sure how long this curve will take to converge.

Thanks for your reply.

The reason why I force player to flat bet is because I just want to know how much EV gain from the strategy change (basic strategy to perfect strategy). I think only MC sims with perfect strategy will give the correct results. Will you help me to solve this problem?

I have done one experiment on my cellphone on a 6-deck stand-17 shoe with a cut card at 4.5/6 deck. I played HiLo deviation strategy all the way and checked computer-perfect strategy only during the 3.5/6-4.5/6 deck interval. What I found is that all these computer-deviations matched up to those HiLo-deviations. I would like to do a couple of more such experiments to research this matter again.

Quote: ssho88

Thanks for your reply.

The reason why I force player to flat bet is because I just want to know how much EV gain from the strategy change (basic strategy to perfect strategy). I think only MC sims with perfect strategy will give the correct results. Will you help me to solve this problem?
link to original post

Yes, I understand why you want to isolate the effect of strategy changes by flat betting.

It will take a few hours to get results that converge for deeper penetration. Running just 100 simulations for each penetration level shows almost no EV gain from computer perfect play until you get past 50% penetration. After that, the effect of strategy optimization builds up quickly. However, if you are flat betting, then you will be losing for the first 60% penetration, at least. You would need a very large advantage in the remaining part of the shoe to overcome these losses. I am guessing you need much more than 75% penetration.

I will have the results for a much larger MC sim by tomorrow.

Quote: Mental

Of course, removing aces and tens affects the EV the most. When all of the tens are removed, I am seeing that the EV tilts towards the player again. I am not sure why this happens. I hope my calculations are correct. Can anyone confirm this?

I summarized your EOR table into a graph. As shown, to be more accurate, removing aces, tens, and fives affects the EV the most. Be confident too. It's correct that when all of the tens are removed, the EV tilts towards the player.

However, this EOR consideration is often based on a perturbation theory on basic strategy; therefore, only the first few columns of your table are meaningful, because people probably will not encounter the remaining in any casinos.

Attached is the graph.

Quote: Mental

Quote: ssho88

Thanks for your reply.

The reason why I force player to flat bet is because I just want to know how much EV gain from the strategy change (basic strategy to perfect strategy). I think only MC sims with perfect strategy will give the correct results. Will you help me to solve this problem?
link to original post

Yes, I understand why you want to isolate the effect of strategy changes by flat betting.

It will take a few hours to get results that converge for deeper penetration. Running just 100 simulations for each penetration level shows almost no EV gain from computer perfect play until you get past 50% penetration. After that, the effect of strategy optimization builds up quickly. However, if you are flat betting, then you will be losing for the first 60% penetration, at least. You would need a very large advantage in the remaining part of the shoe to overcome these losses. I am guessing you need much more than 75% penetration.

I will have the results for a much larger MC sim by tomorrow.
link to original post

Thanks in advance.

I guess the EV gain(50% penetration, flat bet) of perfect play should be around +0.05% to +0.10%. Higher penetration may get higher EV gain.

Quote: ssho88

I guess the EV gain(50% penetration, flat bet) of perfect play should be around +0.05% to +0.10%. Higher penetration may get higher EV gain.
link to original post

Your guesses are not far off. Computer perfect play will gain you 0.05% after three decks and 0.10% after four decks (50% penetration). But the gains really starts to ramp up after seven decks penetration. If you could start a hand after 400 of 416 cards had been seen, then that hand would have an average EV of around +4.9%. This is just an average. Many hands would be -EV. In my simulations, after 10,000 shoes, the worst hand had an EV of -6.5% and the best hand had an EV of +65%. I could go back and try to figure out which stub had such a high EV, but it was probably very rich in aces and tens. I doubt that any counting system would give you the strategy changes for such an extreme shoe.

I will provide EV charts later after the sim finishes.

So if a single deck game pays 6:5 on blackjack, but pays 2:1 on an Ace-Face of spades, how does that compare to a 3:2 game with all the same rules?

Quote: Deucekies

So if a single deck game pays 6:5 on blackjack, but pays 2:1 on an Ace-Face of spades, how does that compare to a 3:2 game with all the same rules?
link to original post

Assume you don’t leave after the A of spades is dealt, etc?

From a fresh deck there are sixty-four ways to make blackjack and 3 of them pay 2:1 (I’m assuming “face” excludes the ten of spades).

6/5 * 61/64 + 2/1 * 3/64 = 1.2375. That’s a lot worse than 3/2 = 1.5.

Quote: Deucekies

So if a single deck game pays 6:5 on blackjack, but pays 2:1 on an Ace-Face of spades, how does that compare to a 3:2 game with all the same rules?
link to original post

Only 3 of 64 naturals qualify. You are effectively being paid 1.24 for BJ, whereas 6:5 pays 1.20 and normal is 1.50.

I did exact calculations of computer perfect EV for 10,000 shoes with N random cards were removed from the shoe and exposed to the player.


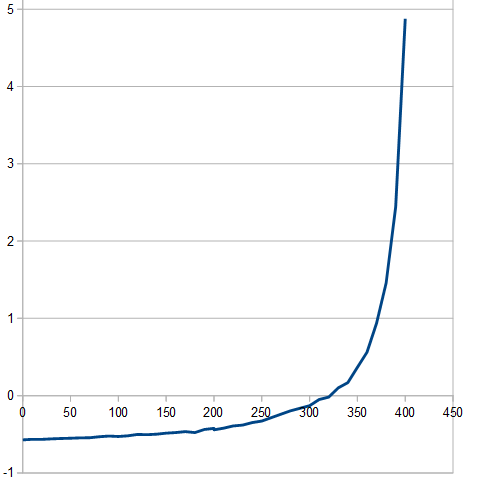
This chart above is the EV in percent of the initial bet for perfect play of a hand where the number of cards that you have seen is given on the X axis. To clarify, the data point at 400 is not the EV of playing a shoe until 400 cards of penetration. Instead, it is the EV of playing a single hand after 400 of 416 cards have been seen.



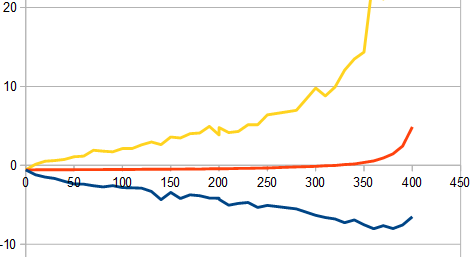
This second chart uses the same data for EV in red, and adds the EV of the best hand in yellow and the worst hand in blue. The 16 random cards in the shoe can be very favorable to the player or favorable to the house just by chance. But computer perfect play allows the player to use the best playing strategy for those 16 random cards.

The overall EV of flat betting through a shoe with computer perfect play would be negative unless the cut cards was at least 402 cards deep into a 8-deck shoe.

Quote Mental: “To clarify, the data point at 400 is not the EV of playing a shoe until 400 cards of penetration. Instead, it is the EV of playing a single hand after 400 of 416 cards have been seen.”

I don’t understand this part, “a single hand.” There are about 340 hands that are listed in Wizard’s basic strategy table, including player hard total, soft hands, and pairs versus dealer each upcard. So, which hand do you choose for this calculation?

Of these 340 hands in the basic strategy table, there are only about 100 hands that lie at the decision boarder lines and thus need a computer-perfect strategy. The majority of the hands are still played with basic strategy. I am confused here.

For example, these hands need special attention:
16 vs. T,
15 vs. T
16 vs. 9,
16 vs. A
T,T vs. 6
T, T vs. 5

Whereas these hands do not need any strategy:
20 vs. 7
19 vs. 8,
16 vs. 6.

There is another easy part. That’s the insurance. Do you include it too?

Quote: Mental

I did exact calculations of computer perfect EV for 10,000 shoes with N random cards were removed from the shoe and exposed to the player.


This chart above is the EV in percent of the initial bet for perfect play of a hand where the number of cards that you have seen is given on the X axis. To clarify, the data point at 400 is not the EV of playing a shoe until 400 cards of penetration. Instead, it is the EV of playing a single hand after 400 of 416 cards have been seen.



This second chart uses the same data for EV in red, and adds the EV of the best hand in yellow and the worst hand in blue. The 16 random cards in the shoe can be very favorable to the player or favorable to the house just by chance. But computer perfect play allows the player to use the best playing strategy for those 16 random cards.

The overall EV of flat betting through a shoe with computer perfect play would be negative unless the cut cards was at least 402 cards deep into a 8-deck shoe.
link to original post

So may I know what is the perfect play flat bet HE when penetration = 50%? EV change from -0.708% to -0.59%+- ?

Quote: ssho88

Quote: Mental

I did exact calculations of computer perfect EV for 10,000 shoes with N random cards were removed from the shoe and exposed to the player.


This chart above is the EV in percent of the initial bet for perfect play of a hand where the number of cards that you have seen is given on the X axis. To clarify, the data point at 400 is not the EV of playing a shoe until 400 cards of penetration. Instead, it is the EV of playing a single hand after 400 of 416 cards have been seen.



This second chart uses the same data for EV in red, and adds the EV of the best hand in yellow and the worst hand in blue. The 16 random cards in the shoe can be very favorable to the player or favorable to the house just by chance. But computer perfect play allows the player to use the best playing strategy for those 16 random cards.

The overall EV of flat betting through a shoe with computer perfect play would be negative unless the cut cards was at least 402 cards deep into a 8-deck shoe.
link to original post

So may I know what is the perfect play flat bet HE when penetration = 50%? EV change from -0.708% to -0.59%+- ?
link to original post

Not even close. That’s the EV of the the last hand at 50% penetration, not the EV over the whole shoe to that point.

Quote: unJon

Quote: ssho88

Quote: Mental

I did exact calculations of computer perfect EV for 10,000 shoes with N random cards were removed from the shoe and exposed to the player.


This chart above is the EV in percent of the initial bet for perfect play of a hand where the number of cards that you have seen is given on the X axis. To clarify, the data point at 400 is not the EV of playing a shoe until 400 cards of penetration. Instead, it is the EV of playing a single hand after 400 of 416 cards have been seen.



This second chart uses the same data for EV in red, and adds the EV of the best hand in yellow and the worst hand in blue. The 16 random cards in the shoe can be very favorable to the player or favorable to the house just by chance. But computer perfect play allows the player to use the best playing strategy for those 16 random cards.

The overall EV of flat betting through a shoe with computer perfect play would be negative unless the cut cards was at least 402 cards deep into a 8-deck shoe.
link to original post

So may I know what is the perfect play flat bet HE when penetration = 50%? EV change from -0.708% to -0.59%+- ?
link to original post

Not even close. That’s the EV of the the last hand at 50% penetration, not the EV over the whole shoe to that point.
link to original post

So may I know what is the perfect play flat bet HE when penetration = 50%?

Quote: aceside

Quote Mental: “To clarify, the data point at 400 is not the EV of playing a shoe until 400 cards of penetration. Instead, it is the EV of playing a single hand after 400 of 416 cards have been seen.”

I don’t understand this part, “a single hand.” There are about 340 hands that are listed in Wizard’s basic strategy table, including player hard total, soft hands, and pairs versus dealer each upcard. So, which hand do you choose for this calculation?
link to original post

You are thinking about a 'specific' hand after the initial deal, but before any action. I am calculating the EV of a 'single' hand before any cards are dealt. Capisce?

The EV of a BJ game is taken to be the EV off the top of the shoe. Ignore the burn card unless you see which card it is. After you see N cards, the optimal EV is different for the next single hand, and different for the hand after that because you have now seen N+X cards.

There are 41 data points to the curve: (N = 0, 10, 20, ... 400 cards seen). For each data point, I create 10,000 random shoes and remove N cards. Then I calculate the computer perfect EV for playing one single hand from each shoe and average over the 10K shoes.

I can approximate the EV of playing until a penetration of 400 out of 416 cards by numerically integrating the EV curve. This cumulative EV is still negative when you get to the hand starting at N=400.

I start to understand you. It is too extreme to consider an 8-deck shoe that deals to a 400/416 card depth. A more reasonable game is a 6-deck shoe stand-17 with a cut card at the 5/6 deck depth, because these games are still available. Also, I like step sizes of 13, 26, 39, 52 etc for card games. Furthermore, I believe that there is not very much juice considering the first half of a shoe.

Quote: aceside

I start to understand you. It is too extreme to consider an 8-deck shoe that deals to a 400/416 card depth. A more reasonable game is a 6-deck shoe stand-17 with a cut card at the 5/6 deck depth, because these games are still available. Also, I like step sizes of 13, 26, 39, 52 etc for card games. Furthermore, I believe that there is not very much juice considering the first half of a shoe.
link to original post

Nothing is too extreme to consider -- just too extreme to be found in the real world.

My point is that index strategy changes don't really matter much until well past OP's 50% penetration. Note that some shoes offer +5% EV opportunities already at 50% penetration. Jumping your bet size in +EV shoes is a much bigger advantage than playing computer perfect deep into every shoe at flat bet.

Online live dealer would allow you to play computer perfect. I don't know what the deepest penetration you can find in a online live dealer situation. I usually see the cut card 50-60% of the way through 8 decks. I also don't know what online casinos would tolerate in terms of bet spread. There are much bigger opportunities in other games, so I don't give shoe BJ much thought.

I researched perfect-insurance play by simulation. The EV gain from playing perfect-insurance with an 8-deck shoe when flat betting all the way is an exponential function of the dealing deck penetration. Attached is a graph.

Quote: aceside

I researched perfect-insurance play by simulation. The EV gain from playing perfect-insurance with an 8-deck shoe when flat betting all the way is an exponential function of the dealing deck penetration. [snip]
link to original post

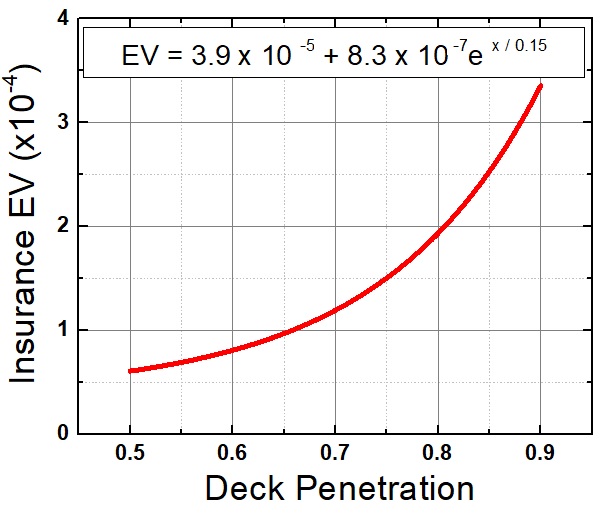
Is this calculation performed using combinatorics to get the probability of an ace? Or is it a sim?

This is a sim, but I can provide a calculation. I am traveling today.

Quote: ssho88

...Penetration = 50%...

Understand this might come off troll, but it's not.... My answer would be to stop being interested in this game after this part of the description. Even if you get a positive player advantage at this online live blackjack game the bankroll and variance swings you'd need to go from straight min to max on the tiny amount of positive situations you'll get (as opposed to deeper pen) would be wild, to say the least. From a theoretical/mathematical standpoint I do find it interesting though.