Poll
 | 1 vote (50%) | ||
 | 1 vote (50%) | ||
| No votes (0%) |
2 members have voted
My argument is for the side bet. There's one called the "Pot of Gold" which you can find more about here. Paytable 2 is what I'm after. The basis is the more free splits and doubles per hand, the more money your side bet makes. What if you waited for an "extremely" low count, and max bet the Pot of Gold? There's less 10's in the deck which means slightly more splits. The cards are also overall lower meaning more 9's 10's and 11's. Does "extremely" happen at a true -7? (HiLo) or maybe at true -1?
My local casino has 1 table open usually and its $5-100 main bet with $1-10 on the side bet where I'm almost certain side bet can't exceed main bet (didn't ask but casino norm is no)
I'd do math but that scares me. tell me what you think in the poll.
How do you get the Pot Of Gold Tokens? I can see doubling down 4 hands, but how do you double down 7 hands? It seems this side bet loses 5/6 of the time, so it will deplete your bankroll while you wait for the big payoff. Seems like another waste.
Quote: ChumpChangeSplits, Double Downs, and Black Jacks are my main source of profit in the game. This Black Jack variation game sounds bad with the 6:5 payout, period.
How do you get the Pot Of Gold Tokens? I can see doubling down 4 hands, but how do you double down 7 hands? It seems this side bet loses 5/6 of the time, so it will deplete your bankroll while you wait for the big payoff. Seems like another waste.
link to original post
Blackjack is 3:2 at my casino along with all the standard rules listed. You get a token for every split/double so for example [If you double anything other than hard 9,10, or 11, (ie. double with real money) you do not get a token]. Dealt 5,5 can be split (more profitable for the side bet) which gives you a token and you draw a 4. You double for free and get another token, you draw a 5 for the other hand, split for free with another token.... and eventually you can get 7 tokens. If the dealer busts 23, you get even money on all tokens + main bet for an $80 gain on a $10 bet. You also get 100:1 on the side bet for 5+ tokens.
if you bet 5-0 ($5 main bet and $0 for side bet) normally, and 10-10 when in the advantage, could you make money in the long term?
Maybe a simple count that only kept track of 10's could work with this one
Quote: acesideIf it were countable, it would not be hi-lo. Itís something else. Also, if itís a double deck, it might.
link to original post
I was also thinking maybe a simple 10 count would work but its always nice integrating something you already know into a new game.
More decks actually favor the player given less impact from non-replacement. 6 decks seems standard and is also at my casino. Whether more decks is favorable for counters is another thing.
crude is an understatement but is good at least for viability. My math shows that you gain the advantage on the pot of gold side bet when there are just 3 10's missing from the deck and it becomes positive EV when just 5 10's are missing and you include the loss on the main bet. These numbers come with a lot of assumptions however. First is that the ONLY cards removed from the deck are 10's. Obviously, this isn't how it works and any non-10 removed brings the advantage towards the house. Second, this assumes the edge on the main bet doesn't change (who knows it could even get better with more free bet opportunities) and assumes the average return for the side bet doesn't change. The latter in this assumption would give the player more advantage if took into account. The third assumption is that every hand is dealt from a fresh shoe. Three decks in and the math completely changes. Perhaps the most important assumption is that my math is right. Comparing my total for the probability of being dealt a 9,10(except pair of 5's), 11 or pair of non-10's I get 0.1699233 from a fresh 6 deck shoe as opposed to wizard's 0.166580, which is a difference of about 3 thousandths. I just ignored this difference for my calculations though.
MY WORK:
I used the formula
z = 24/x * 24/x-1 * 20 + 24/x * 23/x-1 * 9
The splits were easier. 24/x * 23/x-1 to find 1 pair. multiply by 9 for 2-8 and the ace.
Finally add them both
I then took my probability for a dud (0.8300767) - wizard's house edge with splitting 5's (0.0148) divided by the probability of a dealt hand (0.1699233) giving me and average return of 4.79791 (go away sig fig nazis) per win. Then you just multiply that number by the probability of a hit and that gets your relative house edge compared to y = 0.8300767
y\ =z\ \cdot\ 4.79791
y\ =\ 0.8300767
y\ =\ 0.8419
x\ =312
HOW TO COUNT IT?:
I'd imagine it's similar to an ace side count but I don't do that so my way is to calculate true count by quarter decks. Think more intuitively that mathematically. You simply count 10's as they are dealt from the shoe, starting at 0 and increasing by 1. There are 4 10's in every quarter deck so if it looks like there are 5 decks remaining and you have a running 21, you have a true 1. 4 tens per quarter (16 per deck) giving you an excess of 5. Divide the excess by the decks remaining for the true count. My math shows you gain the advantage at a true 1. if there are 2 1/4 decks left and you have a running 69 (nice) you have a true 4. Calculating this on the floor requires you to know your 16 times table. 16,32,48,64,80. You can think that 2 decks left means 64 10's should be gone. You have 5 excess tens plus a whole quarter deck without tens so you add 4 more (because 4 tens in a quarter deck on average) giving you an excess of 9 and a true 4. I know this sounds confusing but once you try it for a bit becomes somewhat intuitive (at least for me).
I wrote some code (gross, nerd) and it shows this side bet is more than beatable. In fact, off the first hand in the shoe, you already have the advantage. This quickly shifts back to the house after about a deck though, as you can see in the graph I included where x is the decks remaining and y is the house edge in percent.
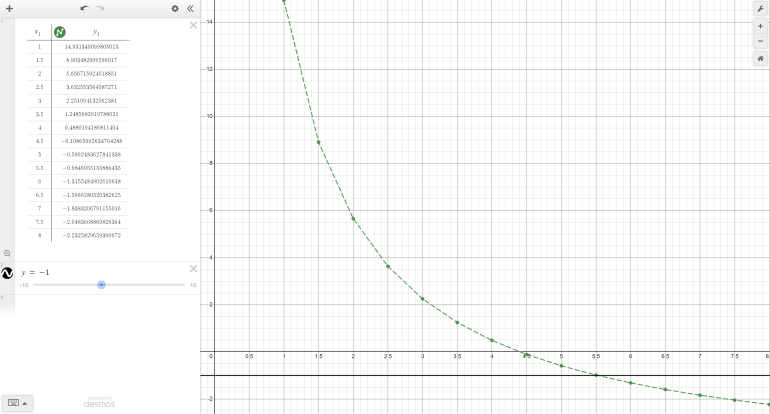
You can actually test any deck composition with the code I made, and as it turns out, the 2 cards that when removed from the deck, give the most advantage, are the 10's and A's. That is exactly what a Hi-Lo counter is looking for. Ideally, you would keep track of 2-7 for low and 9-A for high, but Hi-Lo still gives a decent amount of precision. About 4.5% per true count. This number does go down with a higher true count though. The number increases with fewer decks, being almost triple by the time there are 2 decks left. This does make it more complex to count since the house edge changes drastically with decks unlike normal blackjack. This also means that for the first time ever, more deck penetration is better. You can check all of this out for yourself in a python compiler with the code I wrote. You do NOT need any sort of programming knowledge to be able to mess with this. [ctrl + a ] to copy the whole thing and paste it in the compiler. Just change the numbers in the lines on top
#modify the values for the amount of each card rank left in the deck and for the paytable
decks = 6
twos = decks * 4 # -0.65% per card
threes = decks * 4 # -0.65% per card
fours = decks * 4 # -0.65% per card
fives = decks * 4 # -0.25% per card
sixes = decks * 4 # -0.65% per card
sevens = decks * 4 # -0.65% per card
eights = decks * 4 # -0.25% per card
nines = decks * 4 # +0.13% per card
tens = decks * 16 # +0.8% per card
aces = decks * 4 # +0.5% per card
#4.44% per true count
#everything on a 'to one' basis
one_lammer = 3
two_lammers = 12
three_lammers = 30
four_lammers = 50
five_lammers = 100
six_lammers = 100
seven_lammers = 100
#do not modify anything below this line
deck = twos+threes+fours+fives+sixes+sevens+eights+nines+tens+aces
#print(deck, "cards in the deck.")
double2 = (twos/deck) * ((sevens+eights+nines)/(deck - 1))
double3 = (threes/deck) * ((sixes+sevens+eights)/(deck - 1))
double4 = (fours/deck) * ((fives+sixes+sevens)/(deck - 1))
double5 = (fives/deck) * ((fours+sixes)/(deck - 1))
double6 = (sixes/deck) * ((threes+fours+fives)/(deck - 1))
double7 = (sevens/deck) * ((twos+threes+fours)/(deck - 1))
double8 = (eights/deck) * ((twos+threes)/(deck - 1))
double9 = (nines/deck) * (twos/(deck - 1))
doubles_total = double2+double3+double4+double5+double6+double7+double8+double9
#print(doubles_total, "is the probability for a dealt free double opportunity")
split2 = (twos/deck) * ((twos - 1)/(deck - 1))
split3 = (threes/deck) * ((threes - 1)/(deck - 1))
split4 = (fours/deck) * ((fours - 1)/(deck - 1))
split5 = (fives/deck) * ((fives - 1)/(deck - 1))
split6 = (sixes/deck) * ((sixes - 1)/(deck - 1))
split7 = (sevens/deck) * ((sevens - 1)/(deck - 1))
split8 = (eights/deck) * ((eights - 1)/(deck - 1))
split9 = (nines/deck) * ((nines - 1)/(deck - 1))
splitA = (aces/deck) * ((aces - 1)/(deck - 1))
split_total = split2+split3+split4+split5+split6+split7+split8+split9+splitA
#print(split_total, "is the probability for a dealt free split opportunity")
pat_total = doubles_total + split_total
split2_1_1s0d = split2 * (((deck-2)-(twos-2)-sevens-eights-nines)/(deck-2)) * (((deck-3)-(twos-2)-sevens-eights-nines)/(deck-3))
split3_1_1s0d = split3 * (((deck-2)-(threes-2)-sevens-eights-sixes)/(deck-2)) * (((deck-3)-(threes-2)-sevens-eights-sixes)/(deck-3))
split4_1_1s0d = split4 * (((deck-2)-(fours-2)-sevens-fives-sixes)/(deck-2)) * (((deck-3)-(fours-2)-sevens-fives-sixes)/(deck-3))
split5_1_1s0d = split5 * (((deck-2)-(fives-2)-fours-sixes)/(deck-2)) * (((deck-3)-(fives-2)-fours-sixes)/(deck-3))
split6_1_1s0d = split6 * (((deck-2)-(sixes-2)-fours-fives-threes)/(deck-2)) * (((deck-3)-(sixes-2)-fours-fives-threes)/(deck-3))
split7_1_1s0d = split7 * (((deck-2)-(sevens-2)-fours-twos-threes)/(deck-2)) * (((deck-3)-(sevens-2)-fours-twos-threes)/(deck-3))
split8_1_1s0d = split8 * (((deck-2)-(eights-2)-threes-twos)/(deck-2)) * (((deck-3)-(eights-2)-threes-twos)/(deck-3))
split9_1_1s0d = split9 * (((deck-2)-(nines-2)-twos)/(deck-2)) * (((deck-3)-(nines-2)-twos)/(deck-3))
splitA_1 = splitA * (((deck-2)-(aces-2))/(deck-2)) * (((deck-3)-(aces-2))/(deck-3))
lammer1 = doubles_total+split2_1_1s0d+split3_1_1s0d+split4_1_1s0d+split5_1_1s0d+split6_1_1s0d+split7_1_1s0d+split8_1_1s0d+split9_1_1s0d+splitA_1
print(lammer1, "is the probability for exactly 1 lammer. (", lammer1*one_lammer, "return)")
split2_2_1s1d = split2 * (((deck-2)-(twos-2)-sevens-eights-nines)/(deck-2)) * ((sevens+eights+nines)/(deck - 3)) * 2
split2_2_2s0d = split2 * ((twos-2)/(deck-2)) * (((deck-3)-(twos-3)-sevens-eights-nines)/(deck-3)) * (((deck-4)-(twos-3)-sevens-eights-nines)/(deck-4)) * (((deck-5)-(twos-3)-sevens-eights-nines)/(deck-5)) * 2
split3_2_1s1d = split3 * (((deck-2)-(threes-2)-sevens-eights-sixes)/(deck-2)) * ((sevens+eights+sixes)/(deck - 3)) * 2
split3_2_2s0d = split3 * ((threes-2)/(deck-2)) * (((deck-3)-(threes-3)-sevens-eights-sixes)/(deck-3)) * (((deck-4)-(threes-3)-sevens-eights-sixes)/(deck-4)) * (((deck-5)-(threes-3)-sevens-eights-sixes)/(deck-5)) * 2
split4_2_1s1d = split4 * (((deck-2)-(fours-2)-sevens-fives-sixes)/(deck-2)) * ((sevens+fives+sixes)/(deck - 3)) * 2
split4_2_2s0d = split4 * ((fours-2)/(deck-2)) * (((deck-3)-(fours-3)-sevens-fives-sixes)/(deck-3)) * (((deck-4)-(fours-3)-sevens-fives-sixes)/(deck-4)) * (((deck-5)-(fours-3)-sevens-fives-sixes)/(deck-5)) * 2
split6_2_1s1d = split6 * (((deck-2)-(sixes-2)-fours-fives-threes)/(deck-2)) * ((fours+fives+threes)/(deck - 3)) * 2
split6_2_2s0d = split6 * ((sixes-2)/(deck-2)) * (((deck-3)-(sixes-3)-fours-fives-threes)/(deck-3)) * (((deck-4)-(sixes-3)-fours-fives-threes)/(deck-4)) * (((deck-5)-(sixes-3)-fours-fives-threes)/(deck-5)) * 2
split7_2_1s1d = split7 * (((deck-2)-(sevens-2)-fours-twos-threes)/(deck-2)) * ((fours+twos+threes)/(deck - 3)) * 2
split7_2_2s0d = split7 * ((sevens-2)/(deck-2)) * (((deck-3)-(sevens-3)-fours-twos-threes)/(deck-3)) * (((deck-4)-(sevens-3)-fours-twos-threes)/(deck-4)) * (((deck-5)-(sevens-3)-fours-twos-threes)/(deck-5)) * 2
split5_2_1s1d = split5 * (((deck-2)-(fives-2)-fours-sixes)/(deck-2)) * ((fours+sixes)/(deck - 3)) * 2
split5_2_2s0d = split5 * ((fives-2)/(deck-2)) * (((deck-3)-(fives-3)-fours-sixes)/(deck-3)) * (((deck-4)-(fives-3)-fours-sixes)/(deck-4)) * (((deck-5)-(fives-3)-fours-sixes)/(deck-5)) * 2
split8_2_1s1d = split8 * (((deck-2)-(eights-2)-threes-twos)/(deck-2)) * ((threes+twos)/(deck - 3)) * 2
split8_2_2s0d = split8 * ((eights-2)/(deck-2)) * (((deck-3)-(eights-3)-threes-twos)/(deck-3)) * (((deck-4)-(eights-3)-threes-twos)/(deck-4)) * (((deck-5)-(eights-3)-threes-twos)/(deck-5)) * 2
split9_2_1s1d = split9 * (((deck-2)-(nines-2)-twos)/(deck-2)) * (twos/(deck - 3)) * 2
split9_2_2s0d = split9 * ((nines-2)/(deck-2)) * (((deck-3)-(nines-3)-twos)/(deck-3)) * (((deck-4)-(nines-3)-twos)/(deck-4)) * (((deck-5)-(nines-3)-twos)/(deck-5)) * 2
splitA_2 = splitA * ((aces-2)/(deck-2)) * (((deck - 3)-(aces-3))/(deck-3)) * (((deck - 4)-(aces-3))/(deck-4)) * (((deck - 5)-(aces-3))/(deck-5)) * 2
lammer2 = split2_2_1s1d+split2_2_2s0d+split3_2_1s1d+split3_2_2s0d+split4_2_1s1d+split4_2_2s0d+split5_2_1s1d+split5_2_2s0d+split6_2_1s1d+split6_2_2s0d+split7_2_1s1d+split7_2_2s0d+split8_2_1s1d+split8_2_2s0d+split9_2_1s1d+split9_2_2s0d+splitA_2
print(lammer2, "is the probability for exactly 2 lammers. (", lammer2*two_lammers, "return)")
#0.013488 expected
#0.0160091 gotten
split2_3_1s2d = split2 * ((sevens+eights+nines)/(deck-2)) * ((sevens+eights+(nines-1))/(deck-3))
split2_3_2s_1d = split2 * ((twos-2)/(deck-2)) * ((sevens+eights+nines)/(deck-3)) * (((deck-4)-sevens-eights-(nines-1)-(twos-3))/(deck-4)) * (((deck-5)-sevens-eights-(nines-1)-(twos-3))/(deck-5)) * 6
split2_3_3s_0d = split2 * ((twos-2)/(deck-2)) * ((twos-3)/(deck-3)) * (((deck-4)-sevens-eights-nines)/(deck-4)) * (((deck-5)-sevens-eights-nines)/(deck-5)) * (((deck-6)-sevens-eights-nines)/(deck-6)) * (((deck-7)-sevens-eights-nines)/(deck-7)) * 5
split3_3_1s2d = split3 * ((sevens+eights+sixes)/(deck-2)) * ((sevens+eights+(sixes-1))/(deck-3))
split3_3_2s_1d = split3 * ((threes-2)/(deck-2)) * ((sevens+eights+sixes)/(deck-3)) * (((deck-4)-sevens-eights-(sixes-1)-(threes-3))/(deck-4)) * (((deck-5)-sevens-eights-(sixes-1)-(threes-3))/(deck-5)) * 6
split3_3_3s_0d = split3 * ((threes-2)/(deck-2)) * ((threes-3)/(deck-3)) * (((deck-4)-sevens-eights-sixes)/(deck-4)) * (((deck-5)-sevens-eights-sixes)/(deck-5)) * (((deck-6)-sevens-eights-sixes)/(deck-6)) * (((deck-7)-sevens-eights-sixes)/(deck-7)) * 5
split4_3_1s2d = split4 * ((sevens+fives+sixes)/(deck-2)) * ((sevens+fives+(sixes-1))/(deck-3))
split4_3_2s_1d = split4 * ((fours-2)/(deck-2)) * ((sevens+fives+sixes)/(deck-3)) * (((deck-4)-sevens-fives-(sixes-1)-(fours-3))/(deck-4)) * (((deck-5)-sevens-fives-(sixes-1)-(fours-3))/(deck-5)) * 6
split4_3_3s_0d = split4 * ((fours-2)/(deck-2)) * ((fours-3)/(deck-3)) * (((deck-4)-sevens-fives-sixes)/(deck-4)) * (((deck-5)-sevens-fives-sixes)/(deck-5)) * (((deck-6)-sevens-fives-sixes)/(deck-6)) * (((deck-7)-sevens-fives-sixes)/(deck-7)) * 5
split5_3_1s2d = split5 * ((fours+sixes)/(deck-2)) * ((fours+(sixes-1))/(deck-3))
split5_3_2s_1d = split5 * ((fives-2)/(deck-2)) * ((fours+sixes)/(deck-3)) * (((deck-4)-fours-(sixes-1)-(fives-3))/(deck-4)) * (((deck-5)-fours-(sixes-1)-(fives-3))/(deck-5)) * 6
split5_3_3s_0d = split5 * ((fives-2)/(deck-2)) * ((fives-3)/(deck-3)) * (((deck-4)-fours-sixes)/(deck-4)) * (((deck-5)-fours-sixes)/(deck-5)) * (((deck-6)-fours-sixes)/(deck-6)) * (((deck-7)-fours-sixes)/(deck-7)) * 3
split6_3_1s2d = split6 * ((fours+fives+threes)/(deck-2)) * ((fours+fives+(threes-1))/(deck-3))
split6_3_2s_1d = split6 * ((sixes-2)/(deck-2)) * ((fours+fives+threes)/(deck-3)) * (((deck-4)-fours-fives-(threes-1)-(sixes-3))/(deck-4)) * (((deck-5)-fours-fives-(threes-1)-(sixes-3))/(deck-5)) * 6
split6_3_3s_0d = split6 * ((sixes-2)/(deck-2)) * ((sixes-3)/(deck-3)) * (((deck-4)-fours-fives-threes)/(deck-4)) * (((deck-5)-fours-fives-threes)/(deck-5)) * (((deck-6)-fours-fives-threes)/(deck-6)) * (((deck-7)-fours-fives-threes)/(deck-7)) * 5
split7_3_1s2d = split7 * ((fours+twos+threes)/(deck-2)) * ((fours+twos+(threes-1))/(deck-3))
split7_3_2s_1d = split7 * ((sevens-2)/(deck-2)) * ((fours+twos+threes)/(deck-3)) * (((deck-4)-fours-twos-(threes-1)-(sevens-3))/(deck-4)) * (((deck-5)-fours-twos-(threes-1)-(sevens-3))/(deck-5)) * 6
split7_3_3s_0d = split7 * ((sevens-2)/(deck-2)) * ((sevens-3)/(deck-3)) * (((deck-4)-fours-twos-threes)/(deck-4)) * (((deck-5)-fours-twos-threes)/(deck-5)) * (((deck-6)-fours-twos-threes)/(deck-6)) * (((deck-7)-fours-twos-threes)/(deck-7)) * 5
split8_3_1s2d = split8 * ((twos+threes)/(deck-2)) * ((twos+(threes-1))/(deck-3))
split8_3_2s_1d = split8 * ((eights-2)/(deck-2)) * ((twos+threes)/(deck-3)) * (((deck-4)-twos-(threes-1)-(eights-3))/(deck-4)) * (((deck-5)-twos-(threes-1)-(eights-3))/(deck-5)) * 6
split8_3_3s_0d = split8 * ((eights-2)/(deck-2)) * ((eights-3)/(deck-3)) * (((deck-4)-twos-threes)/(deck-4)) * (((deck-5)-twos-threes)/(deck-5)) * (((deck-6)-twos-threes)/(deck-6)) * (((deck-7)-twos-threes)/(deck-7)) * 5
split9_3_1s2d = split9 * ((twos)/(deck-2)) * ((twos-1)/(deck-3))
split9_3_2s_1d = split9 * ((nines-2)/(deck-2)) * ((twos)/(deck-3)) * (((deck-4)-(twos-1)-(nines-3))/(deck-4)) * (((deck-5)-(twos-1)-(nines-3))/(deck-5)) * 6
split9_3_3s_0d = split9 * ((nines-2)/(deck-2)) * ((nines-3)/(deck-3)) * (((deck-4)-twos)/(deck-4)) * (((deck-5)-twos)/(deck-5)) * (((deck-6)-twos)/(deck-6)) * (((deck-7)-twos)/(deck-7)) * 5
splitA_3 = splitA * ((aces-2)/(deck-2)) * ((aces-3)/(deck-3)) * 5
lammer3 = split2_3_3s_0d+split2_3_2s_1d+split2_3_1s2d+split3_3_3s_0d+split3_3_2s_1d+split3_3_1s2d+split4_3_3s_0d+split4_3_2s_1d+split4_3_1s2d+split5_3_3s_0d+split5_3_2s_1d+split5_3_1s2d+split6_3_3s_0d+split6_3_2s_1d+split6_3_1s2d+split7_3_3s_0d+split7_3_2s_1d+split7_3_1s2d+split8_3_3s_0d+split8_3_2s_1d+split8_3_1s2d+split9_3_3s_0d+split9_3_2s_1d+split9_3_1s2d+splitA_3
print(lammer3, "is the probability for exactly 3 lammers. (", lammer3*three_lammers, "return)")
split2_4_2s2d = split2 * ((twos-2)/(deck-2)) * ((sevens+eights+nines)/(deck-3)) * ((sevens+eights+(nines-1))/(deck-4)) * (((deck-5)-sevens-eights-(nines-2)-(twos-3))/(deck-5)) * 6
split2_4_3s1d = split2 * ((twos-2)/(deck-2)) * ((twos-3)/(deck-3)) * ((sevens+eights+nines)/(deck-4)) * (((deck-5)-sevens-eights-(nines-1))/(deck-5)) * (((deck-6)-sevens-eights-(nines-1))/(deck-6)) * (((deck-7)-sevens-eights-(nines-1))/(deck-7)) * 20
split3_4_2s2d = split3 * ((threes-2)/(deck-2)) * ((sevens+eights+sixes)/(deck-3)) * ((sevens+eights+(sixes-1))/(deck-4)) * (((deck-5)-sevens-eights-(sixes-2)-(threes-3))/(deck-5)) * 6
split3_4_3s1d = split3 * ((threes-2)/(deck-2)) * ((threes-3)/(deck-3)) * ((sevens+eights+sixes)/(deck-4)) * (((deck-5)-sevens-eights-(sixes-1))/(deck-5)) * (((deck-6)-sevens-eights-(sixes-1))/(deck-6)) * (((deck-7)-sevens-eights-(sixes-1))/(deck-7)) * 20
split4_4_2s2d = split4 * ((fours-2)/(deck-2)) * ((sevens+fives+sixes)/(deck-3)) * ((sevens+fives+(sixes-1))/(deck-4)) * (((deck-5)-sevens-fives-(sixes-2)-(fours-3))/(deck-5)) * 6
split4_4_3s1d = split4 * ((fours-2)/(deck-2)) * ((fours-3)/(deck-3)) * ((sevens+fives+sixes)/(deck-4)) * (((deck-5)-sevens-fives-(sixes-1))/(deck-5)) * (((deck-6)-sevens-fives-(sixes-1))/(deck-6)) * (((deck-7)-sevens-fives-(sixes-1))/(deck-7)) * 20
split5_4_2s2d = split5 * ((fives-2)/(deck-2)) * ((fours+sixes)/(deck-3)) * ((fours+(sixes-1))/(deck-4)) * (((deck-5)-fours-(sixes-2)-(fives-3))/(deck-5)) * 6
split5_4_3s1d = split5 * ((fives-2)/(deck-2)) * ((fives-3)/(deck-3)) * ((fours+sixes)/(deck-4)) * (((deck-5)-fours-(sixes-1))/(deck-5)) * (((deck-6)-fours-(sixes-1))/(deck-6)) * (((deck-7)-fours-(sixes-1))/(deck-7)) * 20
split6_4_2s2d = split6 * ((sixes-2)/(deck-2)) * ((fours+fives+threes)/(deck-3)) * ((fours+fives+(threes-1))/(deck-4)) * (((deck-5)-fours-fives-(threes-2)-(sixes-3))/(deck-5)) * 6
split6_4_3s1d = split6 * ((sixes-2)/(deck-2)) * ((sixes-3)/(deck-3)) * ((fours+fives+threes)/(deck-4)) * (((deck-5)-fours-fives-(threes-1))/(deck-5)) * (((deck-6)-fours-fives-(threes-1))/(deck-6)) * (((deck-7)-fours-fives-(threes-1))/(deck-7)) * 20
split7_4_2s2d = split7 * ((sevens-2)/(deck-2)) * ((fours+twos+threes)/(deck-3)) * ((fours+twos+(threes-1))/(deck-4)) * (((deck-5)-fours-twos-(threes-2)-(sevens-3))/(deck-5)) * 6
split7_4_3s1d = split7 * ((sevens-2)/(deck-2)) * ((sevens-3)/(deck-3)) * ((fours+twos+threes)/(deck-4)) * (((deck-5)-fours-twos-(threes-1))/(deck-5)) * (((deck-6)-fours-twos-(threes-1))/(deck-6)) * (((deck-7)-fours-twos-(threes-1))/(deck-7)) * 20
split8_4_2s2d = split8 * ((eights-2)/(deck-2)) * ((twos+threes)/(deck-3)) * ((twos+(threes-1))/(deck-4)) * (((deck-5)-twos-(threes-2)-(eights-3))/(deck-5)) * 6
split8_4_3s1d = split8 * ((eights-2)/(deck-2)) * ((eights-3)/(deck-3)) * ((twos+threes)/(deck-4)) * (((deck-5)-twos-(threes-1))/(deck-5)) * (((deck-6)-twos-(threes-1))/(deck-6)) * (((deck-7)-twos-(threes-1))/(deck-7)) * 20
split9_4_2s2d = split9 * ((nines-2)/(deck-2)) * ((twos)/(deck-3)) * (((twos-1))/(deck-4)) * (((deck-5)-(twos-2)-(nines-3))/(deck-5)) * 6
split9_4_3s1d = split9 * ((nines-2)/(deck-2)) * ((nines-3)/(deck-3)) * ((twos)/(deck-4)) * (((deck-5)-(twos-1))/(deck-5)) * (((deck-6)-(twos-1))/(deck-6)) * (((deck-7)-(twos-1))/(deck-7)) * 20
lammer4 = split2_4_2s2d+split2_4_3s1d+split3_4_2s2d+split3_4_3s1d+split4_4_2s2d+split4_4_3s1d+split5_4_2s2d+split5_4_3s1d+split6_4_2s2d+split6_4_3s1d+split7_4_2s2d+split7_4_3s1d+split8_4_2s2d+split8_4_3s1d+split9_4_2s2d+split9_4_3s1d
print(lammer4, "is the probability for exactly 4 lammers. (", lammer4*four_lammers, "return)")
split2_5_2s3d = split2 * ((twos-2)/(deck-2)) * ((sevens+eights+nines)/(deck-3)) * ((sevens+eights+(nines-1))/(deck-4)) * ((sevens+eights+(nines-2))/(deck-5)) * 2
split2_5_3s2d = split2 * ((twos-2)/(deck-2)) * ((twos-3)/(deck-3)) * ((sevens+eights+nines)/(deck-4)) * ((sevens+eights+(nines-1))/(deck-5)) * (((deck-6)-sevens-eights-(nines-2))/(deck-6)) * (((deck-7)-sevens-eights-(nines-2))/(deck-7)) * 30
split3_5_2s3d = split3 * ((threes-2)/(deck-2)) * ((sevens+eights+sixes)/(deck-3)) * ((sevens+eights+(sixes-1))/(deck-4)) * ((sevens+eights+(sixes-2))/(deck-5)) * 2
split3_5_3s2d = split3 * ((threes-2)/(deck-2)) * ((threes-3)/(deck-3)) * ((sevens+eights+sixes)/(deck-4)) * ((sevens+eights+(sixes-1))/(deck-5)) * (((deck-6)-sevens-eights-(sixes-2))/(deck-6)) * (((deck-7)-sevens-eights-(sixes-2))/(deck-7)) * 30
split4_5_2s3d = split4 * ((fours-2)/(deck-2)) * ((sevens+fives+sixes)/(deck-3)) * ((sevens+fives+(sixes-1))/(deck-4)) * ((sevens+fives+(sixes-2))/(deck-5)) * 2
split4_5_3s2d = split4 * ((fours-2)/(deck-2)) * ((fours-3)/(deck-3)) * ((sevens+fives+sixes)/(deck-4)) * ((sevens+fives+(sixes-1))/(deck-5)) * (((deck-6)-sevens-fives-(sixes-2))/(deck-6)) * (((deck-7)-sevens-fives-(sixes-2))/(deck-7)) * 30
split5_5_2s3d = split5 * ((fives-2)/(deck-2)) * ((fours+sixes)/(deck-3)) * ((fours+(sixes-1))/(deck-4)) * ((fours+(sixes-2))/(deck-5)) * 2
split5_5_3s2d = split5 * ((fives-2)/(deck-2)) * ((fives-3)/(deck-3)) * ((fours+sixes)/(deck-4)) * ((fours+(sixes-1))/(deck-5)) * (((deck-6)-fours-(sixes-2))/(deck-6)) * (((deck-7)-fours-(sixes-2))/(deck-7)) * 30
split6_5_2s3d = split6 * ((sixes-2)/(deck-2)) * ((fours+fives+threes)/(deck-3)) * ((fours+fives+(threes-1))/(deck-4)) * ((fours+fives+(threes-2))/(deck-5)) * 2
split6_5_3s2d = split6 * ((sixes-2)/(deck-2)) * ((sixes-3)/(deck-3)) * ((fours+fives+threes)/(deck-4)) * ((fours+fives+(threes-1))/(deck-5)) * (((deck-6)-fours-fives-(threes-2))/(deck-6)) * (((deck-7)-fours-fives-(threes-2))/(deck-7)) * 30
split7_5_2s3d = split7 * ((sevens-2)/(deck-2)) * ((fours+twos+threes)/(deck-3)) * ((fours+twos+(threes-1))/(deck-4)) * ((fours+twos+(threes-2))/(deck-5)) * 2
split7_5_3s2d = split7 * ((sevens-2)/(deck-2)) * ((sevens-3)/(deck-3)) * ((fours+twos+threes)/(deck-4)) * ((fours+twos+(threes-1))/(deck-5)) * (((deck-6)-fours-twos-(threes-2))/(deck-6)) * (((deck-7)-fours-twos-(threes-2))/(deck-7)) * 30
split8_5_2s3d = split8 * ((eights-2)/(deck-2)) * ((twos+threes)/(deck-3)) * ((twos+(threes-1))/(deck-4)) * ((twos+(threes-2))/(deck-5)) * 2
split8_5_3s2d = split8 * ((eights-2)/(deck-2)) * ((eights-3)/(deck-3)) * ((twos+threes)/(deck-4)) * ((twos+(threes-1))/(deck-5)) * (((deck-6)-twos-(threes-2))/(deck-6)) * (((deck-7)-twos-(threes-2))/(deck-7)) * 30
split9_5_2s3d = split9 * ((nines-2)/(deck-2)) * ((twos)/(deck-3)) * ((twos-1)/(deck-4)) * ((twos-2)/(deck-5)) * 2
split9_5_3s2d = split9 * ((nines-2)/(deck-2)) * ((nines-3)/(deck-3)) * ((twos)/(deck-4)) * ((twos-1)/(deck-5)) * (((deck-6)-(twos-2))/(deck-6)) * (((deck-7)-(twos-2))/(deck-7)) * 30
lammer5 = split2_5_2s3d+split2_5_3s2d+split3_5_2s3d+split3_5_3s2d+split4_5_2s3d+split4_5_3s2d+split5_5_2s3d+split5_5_3s2d+split6_5_2s3d+split6_5_3s2d+split7_5_2s3d+split7_5_3s2d+split8_5_2s3d+split8_5_3s2d+split9_5_2s3d+split9_5_3s2d
print(lammer5, "is the probability for exactly 5 lammers. (", lammer5*five_lammers, "return)")
split2_6_3s3d = split2 * ((twos-2)/(deck-2)) * ((twos-3)/(deck-3)) * ((sevens+eights+nines)/(deck-4)) * ((sevens+eights+(nines-1))/(deck-5)) * ((sevens+eights+(nines-2))/(deck-6)) * (((deck-7)-sevens-eights-(nines-3))/(deck-7)) * 20
split3_6_3s3d = split3 * ((threes-2)/(deck-2)) * ((threes-3)/(deck-3)) * ((sevens+eights+sixes)/(deck-4)) * ((sevens+eights+(sixes-1))/(deck-5)) * ((sevens+eights+(sixes-2))/(deck-6)) * (((deck-7)-sevens-eights-(sixes-3))/(deck-7)) * 20
split4_6_3s3d = split4 * ((fours-2)/(deck-2)) * ((fours-3)/(deck-3)) * ((sevens+fives+sixes)/(deck-4)) * ((sevens+fives+(sixes-1))/(deck-5)) * ((sevens+fives+(sixes-2))/(deck-6)) * (((deck-7)-sevens-fives-(sixes-3))/(deck-7)) * 20
split5_6_3s3d = split5 * ((fives-2)/(deck-2)) * ((fives-3)/(deck-3)) * ((fours+sixes)/(deck-4)) * ((fours+(sixes-1))/(deck-5)) * ((fours+(sixes-2))/(deck-6)) * (((deck-7)-fours-(sixes-3))/(deck-7)) * 20
split6_6_3s3d = split6 * ((sixes-2)/(deck-2)) * ((sixes-3)/(deck-3)) * ((threes+fives+fours)/(deck-4)) * ((threes+fives+(fours-1))/(deck-5)) * ((threes+fives+(fours-2))/(deck-6)) * (((deck-7)-threes-fives-(fours-3))/(deck-7)) * 20
split7_6_3s3d = split7 * ((sevens-2)/(deck-2)) * ((sevens-3)/(deck-3)) * ((threes+twos+fours)/(deck-4)) * ((threes+twos+(fours-1))/(deck-5)) * ((threes+twos+(fours-2))/(deck-6)) * (((deck-7)-threes-twos-(fours-3))/(deck-7)) * 20
split8_6_3s3d = split8 * ((eights-2)/(deck-2)) * ((eights-3)/(deck-3)) * ((threes+twos)/(deck-4)) * ((threes+(twos-1))/(deck-5)) * ((threes+(twos-2))/(deck-6)) * (((deck-7)-threes-(twos-3))/(deck-7)) * 20
split9_6_3s3d = split9 * ((nines-2)/(deck-2)) * ((nines-3)/(deck-3)) * ((twos)/(deck-4)) * (((twos-1))/(deck-5)) * (((twos-2))/(deck-6)) * (((deck-7)-(twos-3))/(deck-7)) * 20
lammer6 = split2_6_3s3d+split3_6_3s3d+split4_6_3s3d+split5_6_3s3d+split6_6_3s3d+split7_6_3s3d+split8_6_3s3d+split9_6_3s3d
print(lammer6, "is the probability of exactly 6 lammers. (", lammer6*six_lammers, "return)")
split2_6_3s4d = split2 * ((twos-2)/(deck-2)) * ((twos-3)/(deck-3)) * ((sevens+eights+nines)/(deck-4)) * ((sevens+eights+(nines-1))/(deck-5)) * ((sevens+eights+(nines-2))/(deck-6)) * ((sevens+eights+(nines-3))/(deck-7)) * 5
split3_6_3s4d = split3 * ((threes-2)/(deck-2)) * ((threes-3)/(deck-3)) * ((sevens+eights+sixes)/(deck-4)) * ((sevens+eights+(sixes-1))/(deck-5)) * ((sevens+eights+(sixes-2))/(deck-6)) * ((sevens+eights+(sixes-3))/(deck-7)) * 5
split4_6_3s4d = split4 * ((fours-2)/(deck-2)) * ((fours-3)/(deck-3)) * ((sevens+fives+sixes)/(deck-4)) * ((sevens+fives+(sixes-1))/(deck-5)) * ((sevens+fives+(sixes-2))/(deck-6)) * ((sevens+fives+(sixes-3))/(deck-7)) * 5
split5_6_3s4d = split5 * ((fives-2)/(deck-2)) * ((fives-3)/(deck-3)) * ((fours+sixes)/(deck-4)) * ((fours+(sixes-1))/(deck-5)) * ((fours+(sixes-2))/(deck-6)) * ((fours+(sixes-3))/(deck-7)) * 5
split6_6_3s4d = split6 * ((sixes-2)/(deck-2)) * ((sixes-3)/(deck-3)) * ((threes+fives+fours)/(deck-4)) * ((threes+fives+(fours-1))/(deck-5)) * ((threes+fives+(fours-2))/(deck-6)) * ((threes+fives+(fours-3))/(deck-7)) * 5
split7_6_3s4d = split7 * ((sevens-2)/(deck-2)) * ((sevens-3)/(deck-3)) * ((threes+twos+fours)/(deck-4)) * ((threes+twos+(fours-1))/(deck-5)) * ((threes+twos+(fours-2))/(deck-6)) * ((threes+twos+(fours-3))/(deck-7)) * 5
split8_6_3s4d = split8 * ((eights-2)/(deck-2)) * ((eights-3)/(deck-3)) * ((threes+twos)/(deck-4)) * ((threes+(twos-1))/(deck-5)) * ((threes+(twos-2))/(deck-6)) * ((threes+(twos-3))/(deck-7)) * 5
split9_6_3s4d = split9 * ((nines-2)/(deck-2)) * ((nines-3)/(deck-3)) * ((twos)/(deck-4)) * (((twos-1))/(deck-5)) * (((twos-2))/(deck-6)) * (((twos-3))/(deck-7)) * 5
lammer7 = split2_6_3s4d+split3_6_3s4d+split4_6_3s4d+split5_6_3s4d+split6_6_3s4d+split7_6_3s4d+split8_6_3s4d+split9_6_3s4d
print(lammer7, "is the probability for exactly 7 lammers. (", lammer7*seven_lammers, "return)")
lammer_total = lammer1+lammer2+lammer3+lammer4+lammer5+lammer6+lammer7
print(lammer_total, "is the probability for at least 1 lammer (added) vs", pat_total, "(calculated) or", pat_total-lammer_total, "difference")
returns = ((lammer1*one_lammer)+(lammer2*two_lammers)+(lammer3*three_lammers)+(lammer4*four_lammers)+(lammer5*five_lammers)+(lammer6*six_lammers)+(lammer7*seven_lammers))
house_edge = ((1-pat_total)-returns)
print(house_edge*100, "% is the house edge. (negative numbers favor the player)")
MY QUESTIONS:
Why are my numbers so different from those on Wizard's page ? My house edges do not average whereas Wizard's might? If you average the first 4 decks of play you get close to the 1.5% of Wizard's. What about the individual lammer probabilities? I'm stumped
with this since they should be different since Wizard never splits 5's, but this should also lower my probability for a single lammer, and increase the rest. My probability for 1 is increased too. I got the number for the probability of each lammer added up vs the probability of at least one lammer (which should be equal) to a difference of 66 millionths of a percent, which should be good enough.
Why is it so volatile? You start the shoe with a 1.3% advantage but if even so much as the burn card is a 2, it's suddenly in the house's favor. 5 decks in, a single 10 can change the edge by a whole 4%. The difference between the first hand and last hand of the shoe is about 16%. Normal blackjack takes a dozen high cards to shift the edge by a percent. Why is this bet so volatile?
Is it even worth counting with the volatility? normal blackjack is just about as volatile as a coinflip, but this side has long streaks of nothing followed by high payouts. Sure you have the advantage, but is it worth the risk/reward only being able to play so many hours in your lifetime?
Is it even worth counting with the low table limits? The side bet limit is $10 which for me, is my table limit anyways with a ~8k bankroll. Would professionals ever find use in this? Perhaps if you just arrive at a casino in the middle of nowhere and get backed off from normal blackjack right away, it would be in your interest to play free bet with this side bet if they have it.
Does this pay for the losses? You have to be playing the main game still remember. If betting a plain $5 when disadvantaged and 2 spots of $10 on the side bet when advantaged, would you make money? Assuming you are in the advantage 30% of the time and the average player edge is 2%, and the disadvantage is 1.5%, would would win $18.75 an hour with 100 hands. My next challenge would be to figure out how true count affects the base game which is way above my skillset.
COUNTING GUIDE:
Use the Hi-Lo counting system
Keep in mind using this system does not keep track of 7-9. If there are more of these cards in the deck than their average composition would suggest, you would have a higher edge without knowing it vice-versa
If you do decide to keep track of 7s and 9s (where 7 is low and 9 is high), wait for 1 card lower in the count before you make your decisions
I will be assuming the house edge on the main bet is 1% when the side bet is advantageous
The values I give are the break-even points so max betting here would skyrocket your risk of ruin
5.5 - 6 decks left: bet with an even count or lower
4.5 - 5.5 decks left: bet with any negative count
3 - 4.5 decks left: bet with any running -2 or lower
2 - 3 decks left: bet with any running -3 or lower
1 - 2 decks left: bet with any running -4 or lower
Quote: acesideI regret I voted nah for your survey, but Iíve never played this game and thought this is a 6:5 blackjack payout game. Itís clear you have every skills for beating this game, including math derivation and python coding. Iíd like to read more into this part.
link to original post
I don't blame you but I have that small casino privilege. I'm really glad you think I have the skills :D I just hope my math is accurate


