Question on Wizard's Blackjack Hand Calculator

Does the Expectation for "Hit" assume one card and one card ONLY is drawn by the player? Thanks.

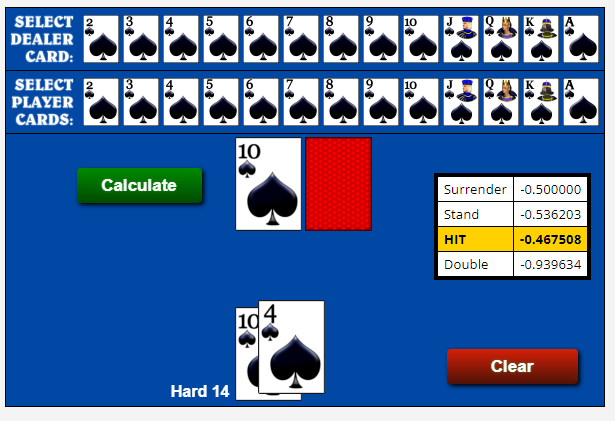
Quote: railer

Does the Expectation for "Hit" assume one card and one card ONLY is drawn by the player? Thanks.

I believe that is the final expectation of the hand and does not assume a single hit.

Thanks. So, the obvious follow up question.... how is the expectation calculated then?

brute force. Take the cards in question and run thru every possible combination.

OK. So, what kind of "brute force" is it? Does the player stop hitting when he reaches 17 or higher?

I am confirming what has been said. The hit option assumes you will hit as many cards as needed according to perfect strategy. So, yes you always stop at hard 17 (versus 7-A) unless you have input a weird "shoe composition".

Quote: DRich

I believe that is the final expectation of the hand and does not assume a single hit.
link to original post

That is correct. It assumes the play follows optimal strategy the rest of the hand, after the play in question.

Quote: Wizard

That is correct. It assumes the play follows optimal strategy the rest of the hand, after the play in question.
link to original post

That's really impressive.

So if I understand this correctly, ...the expectation*probability is calculated for the player hand being hit once with every possible card... then the program calculates the expectation and probability of each decision point (hit or stand) after that... choosing the best decision given the remaining subset of cards?

Quote: railer

Quote: Wizard

That is correct. It assumes the play follows optimal strategy the rest of the hand, after the play in question.
link to original post

That's really impressive.

So if I understand this correctly, ...the expectation*probability is calculated for the player hand being hit once with every possible card... then the program calculates the expectation and probability of each decision point (hit or stand) after that... choosing the best decision given the remaining subset of cards?
link to original post

Yes. That's correct. It is one of two internet BJ hand calculators that do this. The other one is bjstrat. The answers between the two calculators have been extensively checked and are equivalent. Wizard's calculator provides 6 digits of accuracy to the right of the decimal point, whereas the bjstrat calculator only provides 4 digits. The bjstrat calculator does provide some other output information not available on the Wizard's calculator, such as probability of dealer outcomes.

Quote: railer

So if I understand this correctly, ...the expectation*probability is calculated for the player hand being hit once with every possible card... then the program calculates the expectation and probability of each decision point (hit or stand) after that... choosing the best decision given the remaining subset of cards?
link to original post

That's right.

Quote: Wizard

Quote: railer

So if I understand this correctly, ...the expectation*probability is calculated for the player hand being hit once with every possible card... then the program calculates the expectation and probability of each decision point (hit or stand) after that... choosing the best decision given the remaining subset of cards?
link to original post

That's right.
link to original post

Isn't this what is meant by brute force or am I using the term incorrectly?

I remember looking at 14s vs 10 and what it does is assume at each stage the player makes the best decision (ignoring splitting scenarios which doesn't apply here).

So yes it will look at what happens if you stand T4 vs T.

Then it would look at the possible hitting outcomes via T4A ,T42, T43, T44 etc vs T, and because you hit T4A will look at T4AA, T4A2 etc.
You can actually check this using a spreadsheet, since the combinations of hands that the dealer can make (given they don't have a face down Ace) isn't that large. You do this by taking out (e.g. T4AA,T) and starting with a non-Ace working through all the hands the dealer could make.

If I recall correctly you land up with a manageable number of sheets (e.g. "T4A4" vs T) where you look at the chances of standing on T4A4. This is plugged into the T4A analysis. One problem you need to include is the knowledge that the Dealer does not have an Ace, so the chances of the Player's next card is affected by this.

Quote: Wizard

Quote: railer

So if I understand this correctly, ...the expectation*probability is calculated for the player hand being hit once with every possible card... then the program calculates the expectation and probability of each decision point (hit or stand) after that... choosing the best decision given the remaining subset of cards?
link to original post

That's right.
link to original post

That's amazing. How did you do this?

I was able to create a script that can compute 16 vs.10 and match your results exactly (with one minor exception). I enumerated all possible dealer draws with a 10... there's only 288 of them. Then calculated the probability of the 288 dealer draws against a player hitting to an A,2,3,4,5,6,7,8,9,10. I summed the results...and divided by (1-aces/totalcards), because the dealer checked for blackjack but didn't have it.

Admittedly, my script is not "forward looking" to the very rare situation where the composition of the deck is such that a player would hit on 16...then choose to hit on 17... so my results are not quite exact for every deck composition.

But, with a hand like 2,2 vs. 2 the combinatorics just explode, because you'd have to check every possible decision point for hit/stand.... not to mention evaluating split expectations and comparing every result to every result. Wow.

After trying this myself, I'm just so impressed by your calculator. What was your method? Thanks.

Quote: charliepatrick

I remember looking at 14s vs 10 and what it does is assume at each stage the player makes the best decision (ignoring splitting scenarios which doesn't apply here).

So yes it will look at what happens if you stand T4 vs T.

Then it would look at the possible hitting outcomes via T4A ,T42, T43, T44 etc vs T, and because you hit T4A will look at T4AA, T4A2 etc.
You can actually check this using a spreadsheet, since the combinations of hands that the dealer can make (given they don't have a face down Ace) isn't that large. You do this by taking out (e.g. T4AA,T) and starting with a non-Ace working through all the hands the dealer could make.

If I recall correctly you land up with a manageable number of sheets (e.g. "T4A4" vs T) where you look at the chances of standing on T4A4. This is plugged into the T4A analysis. One problem you need to include is the knowledge that the Dealer does not have an Ace, so the chances of the Player's next card is affected by this.
link to original post

The way I looked at all the dealer hands was I wrote a short script and plugged in the rules the dealer must follow. The script produced all of the combinations of dealer draws when the dealer has a TEN.

So, for instance, the first hand is... Dealer 10 --> 2, Ace, Ace, Ace, Ace, Ace. Once I have that, I can compute the probability of the dealer drawing to that hand, given the remaining subset of cards.

That's a good point about how after the Dealer checks for an Blackjack ...there's a slightly greater chance the player will be dealt an Ace. I didn't account for that. Since my results match the Wiz's exactly, I don't think the calculator does either. It would probably make a good bit of difference for doubling 10 vs. 10, which of course isn't a basic strategy play, but does occur rather frequently in single deck when using combinatoric analysis.

Apologies — this isn't quite the correct thread.

I played the Wizard of Odds card-counting blackjack game and it said hitting with my hard 13 against an A wasn't the best play. I could not believe it, and a check of the simple strategy guide backs me up. Am I missing something here (see screenshot)?

(I played the hand out, and the dealer had blackjack — could that be a coding problem?)

Quote: smoothgrh

Apologies — this isn't quite the correct thread.

I played the Wizard of Odds card-counting blackjack game and it said hitting with my hard 13 against an A wasn't the best play. I could not believe it, and a check of the simple strategy guide backs me up. Am I missing something here (see screenshot)?

(I played the hand out, and the dealer had blackjack — could that be a coding problem?)


link to original post

I think it would depend on what the count is. For basic strategy you would hit it but if the count is very high standing would make sense.

Ah, that would make sense. I'm quite sure the count was nearly at even at that point.

I have no explanation for the results you show on the calculator, but I doubt it has anything to do with the count. The image in your post shows that standing on hard 13 vs Ace is 13+ percentage points better than hitting. That's a large swing in the EV of those two options, and I doubt that is caused by an excess of 10s in the shoe. Note that the largest reason to avoid hitting 13 would be a shoe depleted in 8s and 7s - and most counts don't even consider the abundance of 8s and 7s.

Furthermore - I don't know of any blackjack game on WoO that gives recommendations as a function of the count. If I'm wrong then someone post here and correct this statement.

So, I maintain that the result being shown by OP has yet to be explained.