The effect of this that after the round is completed the next card dealt on the first box of the new round is not contaminated by the cards placed back into the machine.
So with 6 decks in the machine logic tells me that if the end count of the previous deal is +6 or more there is a tiny edge with a 6 deck shoe.
However we only get the first card uncontaminated by the previous cards dealt in the last round( that we know of for sure).
Question:
So if you get dealt 1 card from a true one 6 deck shoe and play the rest of the hand out from the 311 cards ( by virtue of the discards from previous round being shuffled back in ) do you have an edge regardless of how small it is?
Assume a wonging game. You either bet the max or zero.
However I am still waiting for a precise answer....
Is there an edge in the game I described. Another way of describing it would be:
Get 6 decks take out a a random 10 - 13 cards that add up to a count of + 6 or more.
Then deal your self the next card.
Shuffle the 10 - 13 cards back into the 6 decks and deal playout the rest of the hand.
I am assuming no hopper / dump.
If there is a dump or hopper as you say then this machine is better than we thought and can definitely be beaten with wonging. ( Either a Zero or Max $ bet )
A running count of +6 on a six deck game is going to be barely better than a +1 true count, which add roughly 0.5% to the player. But that +1 is only for the first card. The second and third player cards, as well as the two or more dealer cards are all coming at +0. So I would say an average of about 1 card at +1 (or +0.5%) and 4.5 cards at +0 (or +0%). Algebra says that adds about 0.1% to the player advantage (or reduces the house advantage by 0.1%). Obviously just an estimate, not an actual result, but a hi-lo count itself is really just an estimate of the player edge based on the deck composition.
The advantage at a true +1 eliminates the house edge and gives us a player edge over and above the house edge.
I believe it to be lower than your thoughts of 0.5% but that is academic. We can both agree that the player has an edge.
0.1% to the player and reducing the house edge by 0.1% are 2 different things unless I am misunderstanding your post.
You either are saying the house edge is .1% less or the player edge is .1% more. Please clarify. Thank you.
If the house edge decreases by 0.1%, that means the player edge must increase by 0.1%. If a blackjack game has a house edge of 0.66%, then the player edge must be -0.66%. If the house edge of this game decreases by 0.1% to 0.56%, the player edge must increase to -0.56%.
Quote: TomGHouse edge + player edge = 0.
Tell that to the tax man.
Quote: unJonTell that to the tax man.
They don't care if you have an advantage or not, they just care if you win.
Quote: SalthouseThis particular CSM spits out the next card to be dealt immediately when the previous card is dealt.
The effect of this that after the round is completed the next card dealt on the first box of the new round is not contaminated by the cards placed back into the machine.
So with 6 decks in the machine logic tells me that if the end count of the previous deal is +6 or more there is a tiny edge with a 6 deck shoe.
However we only get the first card uncontaminated by the previous cards dealt in the last round( that we know of for sure).
Question:
So if you get dealt 1 card from a true one 6 deck shoe and play the rest of the hand out from the 311 cards ( by virtue of the discards from previous round being shuffled back in ) do you have an edge regardless of how small it is?
Assume a wonging game. You either bet the max or zero.
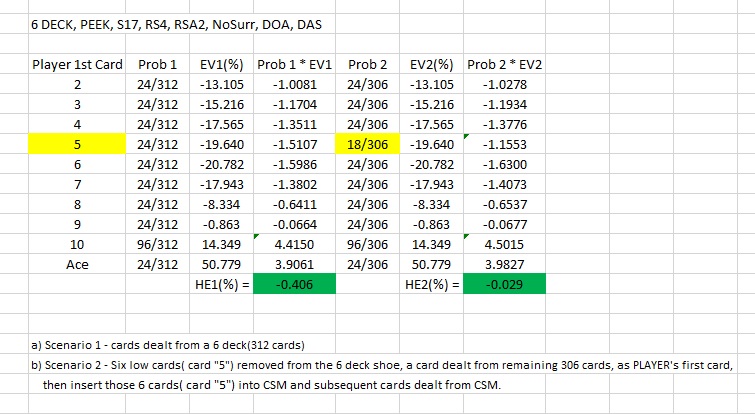
If you remove 6 low cards (card "5") from 6 deck shoe, you can lower the house edge from -0.406% to -0.029%.
See picture below.
I tip my hat to you.
I tip my hat to you.
Quote: ssho88If you remove 6 low cards (card "5") from 6 deck shoe, you can lower the house edge from -0.406% to -0.029%.
See picture below.
No clue how you compute your numbers but a very reliable source "bjstrat.net" gives the following for these rules which seem to be exactly those you give: 6 decks, S17, DAS, SP3 (4 hands) and NoRSA (Aces only split once).
Basic Advantage to player: -0.4029% (close to what you calculated)
If like you mention you remove 6 cards of value "5", then the player advantage shift to +0.4001% for a delta of 0.803%
http://www.bjstrat.net/cgi-bin/cdca.cgi
Quote: GManNo clue how you compute your numbers but a very reliable source "bjstrat.net" gives the following for these rules which seem to be exactly those you give: 6 decks, S17, DAS, SP3 (4 hands) and NoRSA (Aces only split once).
Basic Advantage to player: -0.4029% (close to what you calculated)
If like you mention you remove 6 cards of value "5", then the player advantage shift to +0.4001% for a delta of 0.803%
http://www.bjstrat.net/cgi-bin/cdca.cgi
All EV values in columns 3 and 6 are generated by simulations
"If like you mention you remove 6 cards of value "5", then the player advantage shift to +0.4001% for a delta of 0.803%"
I think what you mentioned above is not the same as what we are talking about . . . .6 cards of value "5" remove from the shoe, dealt a card to PLAYER, then insert those 6 cards of value "5" into CSM(with 305 cads), shuffle that 311(305+6) cards BEFORE dealt a second card to PLAYER . . .
If this is not what you want to say, fine!
What you're now saying is: If we remove 6 low cards (card "5") from a 6 decks shoe, the first card dealt from this shoe will show on average a player edge of 0.4001%
However, since we put back into the shoe the 6 low cards (card"5") previously retired before the second card to the player is dealt, the average player edge for this hand drops to -0.029%
Right ?
Quote: ssho88All EV values in columns 3 and 6 are generated by simulations<snip>
ssho88,
Why are the EV's exactly the same for each row in Columns 3 & 6? Wouldn't removing six 5's have ANY effect on the EV's?
Dog Hand
Quote: DogHandssho88,
Why are the EV's exactly the same for each row in Columns 3 & 6? Wouldn't removing six 5's have ANY effect on the EV's?
Dog Hand
The low cards only remove " temporary " from the shoe, after dealt first card to PLAYER, all those low cards will put back into CSM and shuffle, so the EV should be the same for both scenarios. The EV is for hand that you already know the first card value.
For scenario 2, removal(temporary) of low cards will increase the chance of getting high card for first card, after put back those low cards into csm, it is the same as Scenario 1...... Agree?
I agree that my wording in the sentence above is incorrect and misleading. Sorry for the inconvenience caused
"we put back into the shoe the 6 low cards (card"5") previously retired before the second card to the player is dealt, the average player edge for this hand drops to -0.029%"
That's correct !
Unless there is a hopper/dump of pure cards uncontaminated by the discards being put back in waiting to be dealt
I think although a smaller house edge it does not cross over to a player advantage.


