Poll
 | 10 votes (66.66%) | ||
 | 1 vote (6.66%) | ||
 | 1 vote (6.66%) | ||
 | 2 votes (13.33%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) | |||
| No votes (0%) | |||
 | 4 votes (26.66%) |
15 members have voted
This post shall address my initial analysis, which I open up for peer review.
First, let's establish some baseline rules:
- Dealer hits soft 17
- Blackjack pays 3 to 2
- Dealer peeks for blackjack
- Player may double after a split
- Player may NOT surrender
- Player may re-split up to four hands, including aces
- Continuous shuffler used
- Total-dependent basic strategy followed
My house edge calculator shows the house edge as follows:
- One deck = 0.014%
- Eight decks = 0.577%
This makes the effect of the difference in number of decks 0.563%.
Before I go on, all figures in this analysis are the result of billions of hands played by random simulation.
Let's work on this like an onion, starting with a simplistic balanced version of blackjack and then add the effects of the rules that are not equal both ways.
Imagine a blackjack game where the player follows a "mimic the dealer" strategy of hitting to 17 and also hitting a soft 17. Also let a winning blackjack pays 1-1. Finally, add a rule that if both the player and dealer bust, that the result is a push. This game is perfectly balanced for a zero house edge.
Next, let's remove the rule about a push if both player and dealer bust. Instead, we use the real blackjack rule that if both the player and dealer bust, then the dealer wins. Here is the player expected value adding that rule for one and eight decks:
- One deck = -8.237%
- Eight decks = -8.157%
- Difference = -0.079%.
Why does the player lose more with a single deck? It's because there is more busting on both sides in a single-deck game, resulting in more double busts. The absolute value of the percentages above, to be exact. Why is there more busting with a single deck? I figure it's because both sides are hitting hands with more small cards than large, resulting in hitting into a deck/shoe that is high-card rich. This effect of removal is simply stronger with a single deck.
Next, let's consider the value of a blackjack paying 3-2. It is easy to calculate the effect of this mathematically, as follows:
| Decks | Prob player BJ | Prob dealer BJ | Prob winning BJ | Value |
|---|---|---|---|---|
| 1 | 4.827% | 3.673% | 4.649% | 2.325% |
| 8 | 4.745% | 4.605% | 4.527% | 2.263% |
| Diff | 0.081% | -0.932% | 0.123% | 0.061% |
Here is the effect of the two rule changes thus far. So, the eight-deck game is still a little better.
- Player loses if both bust = -0.079%
- Blackjack pays 3-2 = 0.061%
- Total = -0.018%
Next, let's improve the player's strategy by using basic strategy with a hard total of 12 to 16, which is:
Player has 13 to 16 vs. dealer 2-6 = Stand
Player has 12 vs. dealer 4-6 = Stand
Otherwise, hit with hard 12 to 16.
Here is the effect of that strategy improvement.
- One deck = 3.703%
- Eight decks = 3.270%
- Difference = 0.433%
So this change in strategy is more helpful with a single deck. I assume this is because hitting with 12 to 16 is more dangerous in a single-deck game, because the 12 to 16 are likely composed of more small cards than large, resulting in hitting into a deck/shoe rich in high cards, thus more busting. In other words, the effect of removal again.
Here is where we are at now of the reason a single-deck game is better for the player.
- Player loses if both bust = -0.079%
- Blackjack pays 3-2 = 0.061%
- Strategic standing on 12 to 16 = 0.433%
- Total = 0.415%
Next, let's add proper doubling strategy. We will use the appropriate basic strategy for the given number of decks. Here is the value of adding doubling the player's game.
- One deck = 1.653%
- Eight decks = 1.380%
- Difference = 0.273%
Doubling is thus much more valuable in a single-deck game than a shoe. I figure it's because the player likely has two small cards when doubling, like a 6 and 5, resulting on doubling into a shoe/deck that is ten-card rich. Again, this effect of removal is stronger with one deck than eight.
Let's update our effect list:
- Player loses if both bust = -0.079%
- Blackjack pays 3-2 = 0.061%
- Strategic standing on 12 to 16 = 0.433%
- Strategic doubling = 0.273%
- Total = 0.689%
The only thing left to change (remember, we are not allowing surrender) is the splitting rule. Here is the effect of adding the appropriate splitting strategy:
- One deck = 0.544%
- Eight decks = 0.669%
- Difference = -0.125%
Interesting! Splitting is more effective in an 8-deck shoe. This should no be surprising as it is harder to form a pair in a single deck game than a shoe. Be be specific, the probabilitiy of getting any pair in two cards is 1/17 = 5.882%. In an eight deck shoe it is 7.470%. Not to get off topic, but it interesting how little splitting actually helps the player. So, there is more splitting and re-splitting going on in the shoe game.
Let's update our table again.
- Player loses if both bust = -0.079%
- Blackjack pays 3-2 = 0.061%
- Strategic standing on 12 to 16 = 0.433%
- Strategic doubling = 0.273%
- Strategic splitting = -0.125%
- Total = 0.563%
As a reminder, the difference from my blackjack house edge calculator matches the 0.563%. Yay!
I love graphs, so here is one of the various effects I looked at.
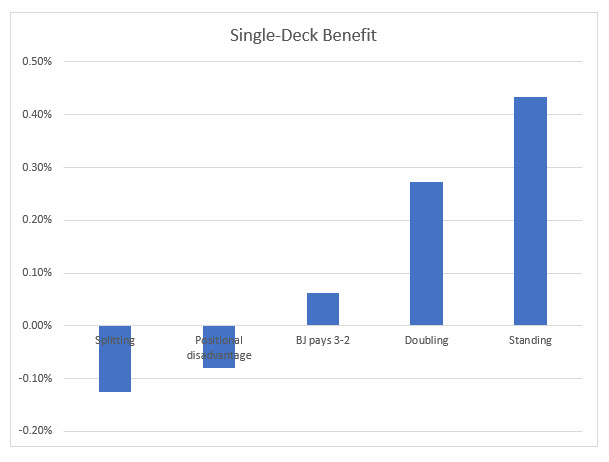
Again, I plan to write this all up in a more formal way and will indclude more details. For now, I open it up to comments and questions. I've been working on this for about a week, so hope to get some feedback.
I would like to thank Don Schlesinger for his help and advice.
Quote: Wizard
Again, I plan to write this all up in a more formal way and will indclude more details. For now, I open it up to comments and questions. I've been working on this for about a week, so hope to get some feedback.
Feedback, well lets use a story. Way back, like 2010, I was on a crew with a guy was no BJ dummy. His dad was a mill guy had to take a late in life dealer job. He knew all the basics. and was a good craps student the night I later taught him. The subject of continuous shufflers came up probably over breakfast or looking at oil leases in the courthouse.
Anyhow, I tried to explain how a CSM gives a slight player edge, having spent more time studying WoV and WoO than on any course I took in college. I kept telling him to read the article on it. A couple weeks of this and I sent him the link and he promised to read it.
At breakfast the next morning he said, "Bro, that was way deeper than I imagined." I had warned him it was, but he still just kind of took it on faith.
"Bro, that was way deeper than I imagined!"
I read this a few times but am still mostly just taking the math on faith. The only thing I could easily explain to a table at a party night is more chance to split because there are more matched cards with more decks. If you explained more of it like that it would be easier to understand.
Picture how I would have to explain it. At a table of people who have probably half of them played before, and most who are not "math people."
The first question I would get would be what is the difference with more decks since the ratio of cards is the same just more. A clump of small cards is as possible as a clump of large cards. At least that is how it appears.
Maybe show how things differ going form 1 to 2 decks, then build on that. Then look at some random hands. Say player 10, 12, and 16. What are my probabilities of hitting 12 on 1 deck vs 2. Ditto 16. Think how many ways to bust a 16 with one deck then 2. How many ways to improve on 1 deck then 2. If I had something that simple, even if for just say 12 and 16 for 1 vs 2 decks I could explain it to people at a table.
IOW, can you show it with cards and not decimals?
Just a thought.
Second, it's always been my policy to teach to near the top. If you put everybody on the bell curve, I try to aim at the person about one standard deviation above average (meaning 84% are less intelligent and 16% are more). There are already plenty of advanced books for those 2 or 3 standard deviations above the norm and plenty of sources for those who need things simplified as much as possible. I aim for those in between.
The topic at hand is complicated and difficult to dumb down. Other sources on this question tend to emphasize that blackjacks are more likely the fewer the decks and the player gets that extra half unit on a winning blackjack. That is pretty easy to explain, but it accounts for about 11% of the total effect of the number of decks only.
Nevertheless, I appreciate the suggestion.
I will read Wizards post several more times in the coming days and weeks, and it is possible some things might click and make sense as time goes on, but the majority of it will remain a foreign language to me. :/
Same thing happened with Don's BJA3. First time I read it....foreign language. Understood almost none of the math, But I applied many of the conclusions. BJA3 happens to be my Bible. I have re-read that 100 times over the years and frequently reference different things, and every once in a while something "clicks" and I say oh yeah that makes sense, but even still most of the math is foreign to me. I am probably the stupidest, most math challenged person on this forum or in the blackjack community. I'm ok with that.
Kind of like a car engine. I drive a vehicle, but if you tell me that the spark tube (The Office mafia episode reference) is bad and needs to be replaced, you are talking a foreign language.
Quote: kewljso in another thread Wizard suggested I take a look at this thread. And so I have. I have to say none of the conclusions surprised me. I knew most of that. But the math to get there....that is another matter. Despite that I play blackjack for a living, I am not a math guy nor understand many of the math and formulas behind things. I take what other, much smarter people than me conclude and apply it. People like Wizard, Don Schlesinger, Doghand and many others.
I will read Wizards post several more times in the coming days and weeks, and it is possible some things might click and make sense as time goes on, but the majority of it will remain a foreign language to me. :/
Same thing happened with Don's BJA3. First time I read it....foreign language. Understood almost none of the math, But I applied many of the conclusions. BJA3 happens to be my Bible. I have re-read that 100 times over the years and frequently reference different things, and every once in a while something "clicks" and I say oh yeah that makes sense, but even still most of the math is foreign to me. I am probably the stupidest, most math challenged person on this forum or in the blackjack community. I'm ok with that.
Kind of like a car engine. I drive a vehicle, but if you tell me that the spark tube (The Office mafia episode reference) is bad and needs to be replaced, you are talking a foreign language.
What about Griffin’s Theory of Blackjack? Fuggedaboudit!
Quote: mcallister3200What about Griffin’s Theory of Blackjack? Fuggedaboudit!
I'm still waiting on the English language version to be published.
Maybe it's just me, but I never quite get over how when you are actually playing you get no sense that any of this is in play. For me in fact I get no sense whatsoever while playing BJ that the real advantage the dealer has is the rule about who busts first. Instead, I might get irritated by how many BJs he gets, how he can draw a bunch of small cards when he needs them, or how often he deals me a 12-16 hand while he so often gets great starting cards. Yeah, 'seemingly' should have been inserted in all the above. The sense I get, though, it doesn't seem like 'seemingly'
Busting rule? Not a hint that is a problem!
In Craps, when playing the darkside, the idea that a 12 rolled on the comeout is a push instead of a win is the real killer is about as hidden an effect as you can possibly experience. I in fact have experienced some awful sessions where a 12 was rolled on the comeout maybe only once the entire time. It is so counter-intuitive to grasp the real reasons the house has an edge in these things!
Quote: odiousgambitIt is so counter-intuitive to grasp the real reasons the house has an edge in these things!
That is one of the essences of a well-designed casino game -- the player doesn't see where the house has the advantage. In blackjack and most poker games it is a player positional disadvantage. The idea to remove the 10's in Spanish 21 was also a good one.
I get asked from time to time by the other side about how to significantly increase the house edge, like by 1%, in blackjack without changing the 3-2 payoff, mandating a side bet, charging a commission on wins, nor change the deck composition in a way the average player won't notice. Nothing good has ever come to mind.
How about dealer wins on a push of 17Quote: WizardThat is one of the essences of a well-designed casino game -- the player doesn't see where the house has the advantage. In blackjack and most poker games it is a player positional disadvantage. The idea to remove the 10's in Spanish 21 was also a good one.
I get asked from time to time by the other side about how to significantly increase the house edge, like by 1%, in blackjack without changing the 3-2 payoff, mandating a side bet, charging a commission on wins, nor change the deck composition in a way the average player won't notice. Nothing good has ever come to mind.
BUT . . .
Blackjack is a compilation of 650 different starting hands - 65 different player hands versus 10 dealer upcard possibilities. When you average effects across all 650 hands -which you always seem to do - you may obscure as much -or more -than you show.
Let's look at some of those 65 player hands against any dealer hand (so I'm averaging across 10 dealer upcards, weighted by probabilities) using your set of BJ rules
96 vs X;___ 1 Deck EV = -39.85% 8 Deck EV = -39.62%
93 vs X;___ 1 Deck EV = -33.04% 8 Deck EV = -31.79%
So we see that both of these player hands are higher EV when they are dealt in an 8 deck game. Why? I know why, and you know why. The best chance of improving a 9-6 is to draw a 6 - but you already hold one of those in your hand. Similarly, a player holding 9-3 is most improved by drawing a 9.
Whereas
65 vs X;_____ 1 Deck EV = 34.43% 8 Deck EV = 31.37%
65 is much lower EV when it is dealt in an 8 deck game. Why? Because when you are doubling down or hitting an 11, you are hoping for a Ten-value card, and you really don't want a 5. Drawing a 6 isn't very exciting either. But the "effect of removal" of the 6 and 5 is much smaller with multiple decks.
You might list the 65 player hands and, for each, show these EV numbers and the probability of these hands for 1 and 8 decks, and actually educate people and give them an AHA! moment so they understand effect of removal and probability of occurrence. You could divide Player BJ Hands into those that are improved by multiple decks and those that are not improved. Maybe to add interest you could highlight the hand that is most hurt by multiple decks and the hand that is most improved by multiple decks. That would "teach" and would show information in a different way than what people have seen before.
Indeed, I've always wondered why the WOO site has a blind spot - why it never shows the EV of starting Blackjack hands so that people can understand the patterns and trends and just how awful and how great certain hands are. That kind of information -the EVs of starting hands- is shown on WOO for UTH and for Mississippi Stud - why is it not shown for Blackjack? You could use colors on grids and make it visually interesting.
I do not want to come across as nagging - I am just trying to help. You asked for feedback! And I am in quarantine until I get my covid test results back (after a contact with someone who has now tested positive), so I have nothing else to do.
https://wizardofodds.com/games/blackjack/player-expected-return/Quote: gordonm888I
Indeed, I've always wondered why the WOO site has a blind spot - why it never shows the EV of starting Blackjack hands so that people can understand the patterns and trends and just how awful and how great certain hands are. That kind of information -the EVs of starting hands- is shown on WOO for UTH and for Mississippi Stud - why is it not shown for Blackjack? You could use colors on grids and make it visually interesting.
Quote: WizardThat is one of the essences of a well-designed casino game -- the player doesn't see where the house has the advantage. In blackjack and most poker games it is a player positional disadvantage. The idea to remove the 10's in Spanish 21 was also a good one.
I get asked from time to time by the other side about how to significantly increase the house edge, like by 1%, in blackjack without changing the 3-2 payoff, mandating a side bet, charging a commission on wins, nor change the deck composition in a way the average player won't notice. Nothing good has ever come to mind.
When Dealer and player both have BJ, they go to war. Player makes an equal bet and each gets one more card and hi card wins, but if the dealer wins, the player just gets paid 1-1 instead of 3-2. It would add some excitement while slightly raising the house edge.
Quote: billryanWhen Dealer and player both have BJ, they go to war, each gets one more card and hi card wins, but if the dealer wins, the player just gets paid 1-1 instead of 3-2. It would add some excitement while slightly raising the house edge.
I really like this idea but how does it increase the house edge since normally this is a push?
Quote: HunterhillHow about dealer wins on a push of 17
I have never seen that, but the player would definitely feel that, given that they are used to that being a push.
Quote: gordonm888IYou might list the 65 player hands and, for each, show these EV numbers and the probability of these hands for 1 and 8 decks, and actually educate people and give them an AHA! moment so they understand effect of removal and probability of occurrence.
I do plan to add such a table, only for all 550 possible starting hands.
Quote:Indeed, I've always wondered why the WOO site has a blind spot - why it never shows the EV of starting Blackjack hands so that people can understand the patterns and trends and just how awful and how great certain hands are.
It does that have, for 12 different sets of rules: Blackjack Expected Values.
Quote: Wizard
I get asked from time to time by the other side about how to significantly increase the house edge, like by 1%, in blackjack without changing the 3-2 payoff, mandating a side bet, charging a commission on wins, nor change the deck composition in a way the average player won't notice. Nothing good has ever come to mind.
You should tell them BJ is good the way it is, that would be at 3:2, not 6:5. 6:5 isn't blackjack in my opinion.
Take a 6 deck game with standard rules (Vegas rules), it looks like a house edge of only about half a percent. But sit down and watch people play. Few people play like me, or you or i dare say the majority of this forum. Most people are making all the wrong plays, everything from mildly wrong, to things like a no bust strategy. Add it all together and the house has more than 1% advantage.
Furthermore, they have the sidebets on most games. I happen to hate most of them because it slows the game down, but it adds to the house edge significantly. Some of these side bets its like a 7-10% house edge. What more do they want? Seems fair the way it is. Let the suckers play sidebets and play stupidly to a higher house edge, while people that want a fair game and learn how to play play to a half percent disadvantage. Add it all up and it's right where it should be. But of course the casino is always looking to expand it's edge.
Quote: gordonm888Blackjack is a compilation of 650 different starting hands ...
This table lists the expected value of all 650 for both one and eight decks under the same rules as my simulation. The values are taken from these expected value tables:
Blackjack expected Returns for one deck and dealer hits on soft 17 and
https://wizardofodds.com/games/blackjack/appendix/9/8dh17r4/
Unlike my simulation study, these tables assume perfect combinatorial strategy at every decision point. This helps in single deck much more than eight decks.
The expected value columns are the product of the expected value of the given situation and the probability of it happening. It is listed in order of the expected value difference, in order of what is best for the player in a single-deck game.
| PLAYER | DEALER | One Deck EV | Eight Deck EV | Difference |
|---|---|---|---|---|
| 10,6 | 10 | -0.006741 | -0.007197 | 0.000456 |
| 10,2 | 10 | -0.004609 | -0.005063 | 0.000454 |
| 10,9 | 10 | 0.001363 | 0.000911 | 0.000452 |
| 10,3 | 10 | -0.005227 | -0.005660 | 0.000433 |
| 10,4 | 10 | -0.005928 | -0.006230 | 0.000302 |
| 10,8 | 10 | -0.002064 | -0.002357 | 0.000293 |
| 10,A | 2 | 0.005792 | 0.005502 | 0.000290 |
| 10,A | 3 | 0.005792 | 0.005502 | 0.000290 |
| 10,A | 4 | 0.005792 | 0.005502 | 0.000290 |
| 10,A | 5 | 0.005792 | 0.005502 | 0.000290 |
| 10,A | 6 | 0.005792 | 0.005502 | 0.000290 |
| 10,A | 7 | 0.005792 | 0.005502 | 0.000290 |
| 10,A | 8 | 0.005792 | 0.005502 | 0.000290 |
| 10,A | 9 | 0.005792 | 0.005502 | 0.000290 |
| 10,A | 10 | 0.020390 | 0.020196 | 0.000194 |
| 10,2 | 2 | -0.000706 | -0.000898 | 0.000191 |
| 8,8 | 10 | -0.000594 | -0.000782 | 0.000188 |
| 10,5 | 5 | -0.000386 | -0.000573 | 0.000186 |
| 10,4 | 4 | -0.000540 | -0.000724 | 0.000183 |
| 6,4 | 5 | 0.000654 | 0.000487 | 0.000167 |
| 6,5 | 4 | 0.000679 | 0.000533 | 0.000146 |
| 10,7 | 10 | -0.005483 | -0.005623 | 0.000140 |
| 6,3 | 5 | 0.000377 | 0.000238 | 0.000139 |
| 9,A | 10 | 0.002010 | 0.001881 | 0.000129 |
| 10,3 | 3 | -0.000758 | -0.000882 | 0.000124 |
| 7,4 | 5 | 0.000698 | 0.000575 | 0.000123 |
| 5,4 | 6 | 0.000415 | 0.000293 | 0.000122 |
| 6,5 | 3 | 0.000607 | 0.000487 | 0.000121 |
| 7,3 | 4 | 0.000549 | 0.000433 | 0.000116 |
| 10,9 | 5 | 0.001718 | 0.001603 | 0.000114 |
| 7,3 | 5 | 0.000593 | 0.000480 | 0.000113 |
| 6,6 | 10 | -0.000513 | -0.000626 | 0.000112 |
| 9,9 | 10 | -0.000177 | -0.000283 | 0.000106 |
| 2,2 | 10 | -0.000366 | -0.000471 | 0.000106 |
| 7,4 | 3 | 0.000590 | 0.000485 | 0.000106 |
| 6,5 | 2 | 0.000547 | 0.000442 | 0.000105 |
| 10,5 | 10 | -0.006663 | -0.006769 | 0.000105 |
| 8,3 | 5 | 0.000675 | 0.000573 | 0.000102 |
| 6,3 | 4 | 0.000278 | 0.000177 | 0.000101 |
| 9,7 | 9 | -0.000349 | -0.000450 | 0.000101 |
| 10,9 | 7 | 0.002356 | 0.002257 | 0.000099 |
| 6,4 | 3 | 0.000482 | 0.000384 | 0.000099 |
| 3,3 | 10 | -0.000457 | -0.000555 | 0.000098 |
| 7,7 | 10 | -0.000678 | -0.000774 | 0.000096 |
| 6,A | 5 | 0.000270 | 0.000177 | 0.000093 |
| 8,2 | 5 | 0.000571 | 0.000478 | 0.000093 |
| 9,7 | 7 | -0.000271 | -0.000364 | 0.000093 |
| 8,7 | 8 | -0.000275 | -0.000366 | 0.000092 |
| 7,4 | 6 | 0.000707 | 0.000617 | 0.000090 |
| 6,4 | 7 | 0.000459 | 0.000369 | 0.000090 |
| 8,7 | 7 | -0.000235 | -0.000324 | 0.000089 |
| 7,2 | 5 | 0.000320 | 0.000232 | 0.000088 |
| 4,4 | 10 | -0.000321 | -0.000407 | 0.000087 |
| 7,2 | 4 | 0.000261 | 0.000175 | 0.000086 |
| 9,2 | 5 | 0.000656 | 0.000570 | 0.000085 |
| 10,9 | A | 0.000570 | 0.000485 | 0.000085 |
| 7,4 | 2 | 0.000523 | 0.000439 | 0.000084 |
| 8,2 | 3 | 0.000465 | 0.000382 | 0.000083 |
| 6,4 | 2 | 0.000416 | 0.000336 | 0.000080 |
| 2,A | 5 | 0.000206 | 0.000126 | 0.000079 |
| 8,3 | 4 | 0.000603 | 0.000525 | 0.000078 |
| 7,3 | 6 | 0.000602 | 0.000525 | 0.000078 |
| 7,A | 4 | 0.000299 | 0.000222 | 0.000077 |
| 9,4 | 9 | -0.000264 | -0.000342 | 0.000077 |
| 8,3 | 2 | 0.000515 | 0.000438 | 0.000077 |
| 6,5 | A | 0.000152 | 0.000075 | 0.000077 |
| 9,8 | 9 | -0.000298 | -0.000375 | 0.000077 |
| 7,3 | 2 | 0.000410 | 0.000335 | 0.000075 |
| 9,5 | 9 | -0.000308 | -0.000382 | 0.000074 |
| 9,6 | 9 | -0.000347 | -0.000420 | 0.000072 |
| 3,A | 5 | 0.000197 | 0.000125 | 0.000072 |
| 5,3 | 6 | 0.000172 | 0.000100 | 0.000072 |
| 8,3 | 6 | 0.000686 | 0.000615 | 0.000071 |
| 7,4 | A | 0.000146 | 0.000074 | 0.000071 |
| 5,4 | 3 | 0.000188 | 0.000118 | 0.000070 |
| 7,2 | 3 | 0.000186 | 0.000117 | 0.000069 |
| 10,4 | 5 | -0.000524 | -0.000592 | 0.000068 |
| 5,4 | 5 | 0.000300 | 0.000233 | 0.000067 |
| 10,9 | 2 | 0.001453 | 0.001386 | 0.000066 |
| 8,6 | 8 | -0.000267 | -0.000330 | 0.000063 |
| 7,A | 5 | 0.000336 | 0.000275 | 0.000061 |
| 8,2 | 4 | 0.000486 | 0.000426 | 0.000060 |
| 8,2 | 6 | 0.000582 | 0.000522 | 0.000060 |
| 8,3 | A | 0.000132 | 0.000073 | 0.000059 |
| 10,3 | 5 | -0.000536 | -0.000593 | 0.000057 |
| 10,9 | 8 | 0.002227 | 0.002171 | 0.000057 |
| 9,2 | 4 | 0.000579 | 0.000522 | 0.000057 |
| 10,6 | 5 | -0.000536 | -0.000593 | 0.000057 |
| 6,2 | 5 | 0.000126 | 0.000071 | 0.000055 |
| 6,5 | 7 | 0.000483 | 0.000429 | 0.000054 |
| 7,5 | 5 | -0.000088 | -0.000142 | 0.000054 |
| 6,6 | 5 | 0.000101 | 0.000048 | 0.000054 |
| 8,4 | 4 | -0.000128 | -0.000180 | 0.000052 |
| 9,2 | 6 | 0.000664 | 0.000612 | 0.000052 |
| 2,A | 6 | 0.000237 | 0.000185 | 0.000052 |
| 10,6 | 7 | -0.001453 | -0.001504 | 0.000052 |
| 6,6 | 4 | 0.000053 | 0.000002 | 0.000052 |
| 6,6 | 2 | -0.000035 | -0.000086 | 0.000051 |
| 8,5 | 5 | -0.000091 | -0.000142 | 0.000051 |
| 4,4 | 5 | 0.000098 | 0.000048 | 0.000050 |
| 9,5 | 5 | -0.000094 | -0.000143 | 0.000049 |
| 6,6 | 3 | 0.000005 | -0.000044 | 0.000049 |
| 10,8 | 5 | 0.000766 | 0.000717 | 0.000049 |
| 9,4 | 4 | -0.000132 | -0.000180 | 0.000049 |
| 7,3 | 8 | 0.000316 | 0.000267 | 0.000049 |
| 4,3 | 5 | 0.000048 | -0.000001 | 0.000048 |
| 4,A | 5 | 0.000170 | 0.000122 | 0.000048 |
| 10,2 | 5 | -0.000547 | -0.000594 | 0.000047 |
| 9,2 | A | 0.000118 | 0.000071 | 0.000047 |
| 3,A | 6 | 0.000231 | 0.000185 | 0.000046 |
| 8,8 | A | -0.000113 | -0.000158 | 0.000046 |
| 9,A | 2 | 0.000630 | 0.000584 | 0.000046 |
| 7,2 | 6 | 0.000329 | 0.000284 | 0.000045 |
| 3,3 | 5 | 0.000111 | 0.000067 | 0.000045 |
| 9,A | 5 | 0.000658 | 0.000614 | 0.000043 |
| 5,3 | 4 | 0.000082 | 0.000039 | 0.000043 |
| 9,8 | 8 | -0.000300 | -0.000343 | 0.000043 |
| 5,3 | 5 | 0.000112 | 0.000069 | 0.000043 |
| 5,4 | 4 | 0.000214 | 0.000172 | 0.000042 |
| 9,2 | 3 | 0.000519 | 0.000477 | 0.000042 |
| 5,A | 6 | 0.000225 | 0.000184 | 0.000041 |
| 5,2 | 5 | 0.000041 | 0.000000 | 0.000041 |
| 8,A | 5 | 0.000443 | 0.000403 | 0.000041 |
| 10,8 | 7 | 0.001501 | 0.001460 | 0.000041 |
| 10,7 | 4 | -0.000259 | -0.000299 | 0.000040 |
| 6,4 | 8 | 0.000306 | 0.000266 | 0.000040 |
| 5,4 | 2 | 0.000108 | 0.000069 | 0.000040 |
| 8,2 | 7 | 0.000402 | 0.000363 | 0.000040 |
| 7,5 | 4 | -0.000143 | -0.000183 | 0.000040 |
| 7,7 | 4 | 0.000068 | 0.000030 | 0.000039 |
| 6,2 | 4 | 0.000077 | 0.000039 | 0.000039 |
| 6,A | 4 | 0.000150 | 0.000112 | 0.000038 |
| 3,2 | 5 | 0.000022 | -0.000016 | 0.000038 |
| 7,7 | 2 | -0.000017 | -0.000055 | 0.000038 |
| 6,3 | 2 | 0.000106 | 0.000068 | 0.000038 |
| 9,A | 7 | 0.000746 | 0.000709 | 0.000037 |
| 5,2 | 6 | 0.000070 | 0.000032 | 0.000037 |
| 3,3 | 4 | 0.000059 | 0.000022 | 0.000037 |
| 7,6 | 4 | -0.000147 | -0.000183 | 0.000036 |
| 4,2 | 5 | 0.000010 | -0.000026 | 0.000036 |
| 6,4 | 10 | 0.000125 | 0.000089 | 0.000036 |
| 8,A | 3 | 0.000401 | 0.000366 | 0.000035 |
| 7,7 | 3 | 0.000021 | -0.000014 | 0.000035 |
| 10,5 | 4 | -0.000711 | -0.000746 | 0.000035 |
| 5,4 | 7 | 0.000195 | 0.000161 | 0.000034 |
| 2,2 | 5 | 0.000110 | 0.000076 | 0.000034 |
| 10,7 | 7 | -0.000351 | -0.000385 | 0.000034 |
| 3,A | 4 | 0.000109 | 0.000075 | 0.000033 |
| 8,A | 2 | 0.000382 | 0.000349 | 0.000033 |
| 8,2 | 9 | 0.000168 | 0.000135 | 0.000033 |
| 9,A | 8 | 0.000758 | 0.000725 | 0.000032 |
| 10,10 | A | 0.003070 | 0.003038 | 0.000032 |
| 4,3 | 6 | 0.000062 | 0.000032 | 0.000031 |
| 8,3 | 7 | 0.000456 | 0.000426 | 0.000031 |
| 10,9 | 6 | 0.001685 | 0.001655 | 0.000030 |
| 6,3 | 7 | 0.000191 | 0.000160 | 0.000030 |
| 6,5 | 8 | 0.000353 | 0.000323 | 0.000030 |
| 7,7 | 8 | -0.000138 | -0.000167 | 0.000029 |
| 4,A | 6 | 0.000211 | 0.000182 | 0.000029 |
| 8,A | 7 | 0.000593 | 0.000565 | 0.000029 |
| 9,A | 6 | 0.000650 | 0.000621 | 0.000028 |
| 4,2 | 6 | 0.000036 | 0.000008 | 0.000028 |
| 8,8 | 9 | -0.000145 | -0.000173 | 0.000028 |
| 9,A | 3 | 0.000619 | 0.000592 | 0.000027 |
| 2,A | 10 | -0.000322 | -0.000349 | 0.000027 |
| 6,6 | 7 | -0.000070 | -0.000097 | 0.000027 |
| 2,2 | 2 | -0.000006 | -0.000033 | 0.000027 |
| 8,A | 6 | 0.000450 | 0.000423 | 0.000027 |
| 10,6 | 8 | -0.001640 | -0.001667 | 0.000027 |
| 5,2 | 4 | -0.000009 | -0.000036 | 0.000026 |
| 9,A | 4 | 0.000628 | 0.000602 | 0.000026 |
| 2,2 | 9 | -0.000080 | -0.000106 | 0.000026 |
| 10,6 | 4 | -0.000722 | -0.000747 | 0.000025 |
| 5,2 | 2 | -0.000071 | -0.000096 | 0.000025 |
| 9,3 | 3 | -0.000185 | -0.000210 | 0.000025 |
| 7,6 | 5 | -0.000122 | -0.000147 | 0.000024 |
| 4,3 | 4 | -0.000011 | -0.000035 | 0.000024 |
| 6,4 | 9 | 0.000159 | 0.000135 | 0.000024 |
| 5,4 | 10 | -0.000488 | -0.000512 | 0.000024 |
| 6,A | A | -0.000112 | -0.000135 | 0.000024 |
| 9,3 | 9 | -0.000284 | -0.000307 | 0.000024 |
| 6,3 | 3 | 0.000136 | 0.000113 | 0.000023 |
| 9,9 | A | -0.000045 | -0.000068 | 0.000023 |
| 8,4 | 5 | -0.000124 | -0.000147 | 0.000023 |
| 9,8 | 10 | -0.001385 | -0.001408 | 0.000023 |
| 4,2 | 4 | -0.000037 | -0.000060 | 0.000023 |
| 7,A | 6 | 0.000350 | 0.000327 | 0.000023 |
| 3,2 | 6 | 0.000039 | 0.000017 | 0.000022 |
| 10,3 | 9 | -0.001386 | -0.001408 | 0.000022 |
| 8,2 | 10 | 0.000110 | 0.000088 | 0.000022 |
| 7,7 | 9 | -0.000172 | -0.000194 | 0.000022 |
| 10,6 | 6 | -0.000418 | -0.000439 | 0.000021 |
| 6,3 | 8 | 0.000113 | 0.000092 | 0.000021 |
| 6,5 | 9 | 0.000232 | 0.000210 | 0.000021 |
| 9,4 | 5 | -0.000127 | -0.000148 | 0.000021 |
| 8,6 | 5 | -0.000127 | -0.000147 | 0.000020 |
| 6,A | 3 | 0.000072 | 0.000052 | 0.000020 |
| 7,A | 3 | 0.000180 | 0.000160 | 0.000020 |
| 6,6 | A | -0.000098 | -0.000118 | 0.000020 |
| 7,6 | 3 | -0.000202 | -0.000222 | 0.000020 |
| 7,3 | 10 | 0.000107 | 0.000088 | 0.000020 |
| 3,A | 10 | -0.000447 | -0.000467 | 0.000020 |
| 3,A | 8 | 0.000034 | 0.000014 | 0.000019 |
| 3,2 | 2 | -0.000092 | -0.000112 | 0.000019 |
| 4,4 | 9 | -0.000074 | -0.000093 | 0.000019 |
| 3,3 | 2 | -0.000039 | -0.000058 | 0.000019 |
| 2,2 | 8 | -0.000051 | -0.000070 | 0.000019 |
| 3,3 | 9 | -0.000112 | -0.000131 | 0.000019 |
| 10,8 | 3 | 0.000525 | 0.000506 | 0.000019 |
| 2,A | 9 | -0.000013 | -0.000032 | 0.000019 |
| 2,2 | 3 | 0.000015 | -0.000004 | 0.000019 |
| 8,A | 10 | 0.000233 | 0.000215 | 0.000018 |
| 4,4 | 6 | 0.000108 | 0.000090 | 0.000018 |
| 8,5 | 3 | -0.000204 | -0.000222 | 0.000018 |
| 2,2 | A | -0.000072 | -0.000090 | 0.000018 |
| 7,A | 8 | 0.000117 | 0.000099 | 0.000018 |
| 7,7 | A | -0.000128 | -0.000146 | 0.000018 |
| 7,2 | 2 | 0.000083 | 0.000065 | 0.000018 |
| 2,A | 4 | 0.000113 | 0.000095 | 0.000018 |
| 9,3 | 5 | -0.000130 | -0.000148 | 0.000018 |
| 9,6 | 5 | -0.000130 | -0.000148 | 0.000018 |
| 3,3 | 8 | -0.000080 | -0.000097 | 0.000017 |
| 7,A | 2 | 0.000123 | 0.000106 | 0.000017 |
| 3,3 | A | -0.000088 | -0.000105 | 0.000017 |
| 4,2 | 2 | -0.000107 | -0.000123 | 0.000017 |
| 8,5 | 4 | -0.000169 | -0.000185 | 0.000016 |
| 2,2 | 4 | 0.000048 | 0.000031 | 0.000016 |
| 4,4 | A | -0.000065 | -0.000081 | 0.000016 |
| 3,3 | 3 | -0.000004 | -0.000020 | 0.000016 |
| 9,2 | 7 | 0.000440 | 0.000424 | 0.000016 |
| 9,9 | 9 | -0.000018 | -0.000034 | 0.000016 |
| 8,6 | 3 | -0.000208 | -0.000223 | 0.000015 |
| 3,3 | 6 | 0.000123 | 0.000108 | 0.000015 |
| 8,4 | 8 | -0.000231 | -0.000246 | 0.000015 |
| 3,2 | 4 | -0.000037 | -0.000052 | 0.000015 |
| 7,3 | 9 | 0.000148 | 0.000133 | 0.000015 |
| 6,3 | 10 | -0.000498 | -0.000513 | 0.000015 |
| 3,A | A | -0.000068 | -0.000083 | 0.000015 |
| 6,2 | 3 | 0.000022 | 0.000007 | 0.000015 |
| 9,4 | 10 | -0.001414 | -0.001428 | 0.000015 |
| 8,A | 4 | 0.000396 | 0.000381 | 0.000014 |
| 6,A | 2 | 0.000014 | -0.000001 | 0.000014 |
| 8,A | 9 | 0.000278 | 0.000264 | 0.000014 |
| 8,6 | 4 | -0.000172 | -0.000186 | 0.000014 |
| 8,5 | 8 | -0.000280 | -0.000294 | 0.000014 |
| 6,6 | 9 | -0.000140 | -0.000153 | 0.000014 |
| 7,A | A | -0.000084 | -0.000098 | 0.000014 |
| 5,4 | 8 | 0.000105 | 0.000091 | 0.000013 |
| 7,5 | 3 | -0.000200 | -0.000213 | 0.000013 |
| 5,3 | 7 | 0.000090 | 0.000077 | 0.000013 |
| 10,3 | 4 | -0.000735 | -0.000748 | 0.000013 |
| 3,2 | 3 | -0.000070 | -0.000083 | 0.000013 |
| 4,A | A | -0.000092 | -0.000105 | 0.000013 |
| 10,9 | 4 | 0.001531 | 0.001518 | 0.000013 |
| 7,2 | 8 | 0.000104 | 0.000091 | 0.000013 |
| 9,5 | 4 | -0.000173 | -0.000186 | 0.000013 |
| 6,2 | 7 | 0.000089 | 0.000077 | 0.000012 |
| 8,7 | 3 | -0.000211 | -0.000223 | 0.000012 |
| 10,8 | 2 | 0.000414 | 0.000403 | 0.000011 |
| 8,7 | 10 | -0.001684 | -0.001695 | 0.000011 |
| 7,7 | 5 | 0.000081 | 0.000070 | 0.000011 |
| 7,7 | 7 | -0.000009 | -0.000020 | 0.000011 |
| 8,5 | 2 | -0.000249 | -0.000260 | 0.000011 |
| 7,6 | 2 | -0.000249 | -0.000260 | 0.000011 |
| 8,8 | 2 | 0.000043 | 0.000032 | 0.000010 |
| 5,2 | 3 | -0.000058 | -0.000069 | 0.000010 |
| 9,6 | 4 | -0.000176 | -0.000186 | 0.000010 |
| 4,3 | 3 | -0.000058 | -0.000068 | 0.000010 |
| 7,6 | 6 | -0.000099 | -0.000109 | 0.000010 |
| 3,A | 9 | -0.000058 | -0.000067 | 0.000010 |
| 6,2 | 2 | -0.000011 | -0.000021 | 0.000010 |
| 10,9 | 3 | 0.001457 | 0.001448 | 0.000009 |
| 5,A | A | -0.000118 | -0.000127 | 0.000009 |
| 8,7 | 4 | -0.000177 | -0.000186 | 0.000009 |
| 2,A | A | -0.000053 | -0.000061 | 0.000009 |
| 7,4 | 9 | 0.000217 | 0.000208 | 0.000008 |
| 8,6 | 2 | -0.000252 | -0.000260 | 0.000008 |
| 8,6 | 6 | -0.000101 | -0.000109 | 0.000008 |
| 5,A | 4 | 0.000065 | 0.000056 | 0.000008 |
| 9,3 | 4 | -0.000178 | -0.000187 | 0.000008 |
| 7,4 | 8 | 0.000328 | 0.000320 | 0.000008 |
| 3,3 | 7 | -0.000015 | -0.000023 | 0.000008 |
| 6,4 | A | 0.000029 | 0.000022 | 0.000008 |
| 6,A | 7 | 0.000058 | 0.000050 | 0.000008 |
| 4,A | 4 | 0.000064 | 0.000057 | 0.000007 |
| 5,5 | 10 | 0.000051 | 0.000044 | 0.000007 |
| 9,5 | 2 | -0.000253 | -0.000260 | 0.000007 |
| 5,3 | 3 | 0.000014 | 0.000007 | 0.000007 |
| 9,8 | 2 | -0.000135 | -0.000142 | 0.000007 |
| 7,A | 9 | -0.000084 | -0.000091 | 0.000007 |
| 8,4 | 3 | -0.000207 | -0.000214 | 0.000007 |
| 6,6 | 8 | -0.000116 | -0.000123 | 0.000007 |
| 4,4 | 8 | -0.000020 | -0.000026 | 0.000007 |
| 7,5 | 7 | -0.000187 | -0.000194 | 0.000007 |
| 4,4 | 3 | 0.000010 | 0.000004 | 0.000006 |
| 6,5 | 5 | 0.000570 | 0.000563 | 0.000006 |
| 4,4 | 4 | 0.000024 | 0.000018 | 0.000006 |
| 7,6 | 7 | -0.000239 | -0.000245 | 0.000006 |
| 6,A | 9 | -0.000130 | -0.000136 | 0.000006 |
| 9,6 | 6 | -0.000104 | -0.000109 | 0.000006 |
| 8,8 | 3 | 0.000070 | 0.000065 | 0.000006 |
| 9,8 | A | -0.000319 | -0.000324 | 0.000005 |
| 9,7 | 4 | -0.000182 | -0.000187 | 0.000005 |
| 4,4 | 2 | -0.000005 | -0.000010 | 0.000005 |
| 2,2 | 6 | 0.000123 | 0.000117 | 0.000005 |
| 10,2 | 4 | -0.000750 | -0.000755 | 0.000005 |
| 8,7 | A | -0.000314 | -0.000319 | 0.000005 |
| 8,7 | 2 | -0.000256 | -0.000260 | 0.000005 |
| 7,3 | A | 0.000026 | 0.000021 | 0.000004 |
| 10,6 | 9 | -0.001851 | -0.001855 | 0.000004 |
| 9,7 | 8 | -0.000413 | -0.000417 | 0.000004 |
| 8,2 | A | 0.000025 | 0.000021 | 0.000004 |
| 10,2 | 3 | -0.000848 | -0.000852 | 0.000004 |
| 7,5 | 6 | -0.000106 | -0.000109 | 0.000004 |
| 5,3 | 2 | -0.000018 | -0.000022 | 0.000004 |
| 9,6 | 2 | -0.000257 | -0.000261 | 0.000003 |
| 6,A | 8 | -0.000063 | -0.000066 | 0.000003 |
| 10,8 | A | -0.000566 | -0.000569 | 0.000003 |
| 9,7 | A | -0.000339 | -0.000341 | 0.000003 |
| 9,4 | A | -0.000267 | -0.000270 | 0.000002 |
| 2,2 | 7 | 0.000006 | 0.000004 | 0.000002 |
| 4,4 | 7 | 0.000040 | 0.000038 | 0.000002 |
| 5,5 | 4 | 0.000213 | 0.000211 | 0.000002 |
| 6,4 | 4 | 0.000423 | 0.000421 | 0.000002 |
| 8,4 | 6 | -0.000108 | -0.000110 | 0.000002 |
| 7,4 | 10 | 0.000606 | 0.000605 | 0.000002 |
| 8,7 | 9 | -0.000428 | -0.000429 | 0.000001 |
| 8,5 | 6 | -0.000109 | -0.000110 | 0.000001 |
| 2,A | 3 | 0.000069 | 0.000068 | 0.000001 |
| 5,5 | A | 0.000011 | 0.000010 | 0.000001 |
| 8,8 | 8 | -0.000011 | -0.000012 | 0.000001 |
| 9,7 | 2 | -0.000260 | -0.000261 | 0.000001 |
| 6,5 | 10 | 0.000605 | 0.000605 | 0.000001 |
| 6,2 | 8 | -0.000054 | -0.000054 | 0.000000 |
| A,A | 9 | 0.000105 | 0.000104 | 0.000000 |
| 8,3 | 9 | 0.000208 | 0.000207 | 0.000000 |
| 5,3 | 8 | -0.000055 | -0.000055 | 0.000000 |
| 5,4 | A | -0.000079 | -0.000079 | 0.000000 |
| 9,7 | 10 | -0.001816 | -0.001815 | 0.000000 |
| 4,A | 7 | 0.000033 | 0.000034 | -0.000001 |
| 5,4 | 9 | -0.000049 | -0.000048 | -0.000001 |
| 6,3 | 9 | -0.000049 | -0.000048 | -0.000002 |
| 9,8 | 5 | -0.000044 | -0.000042 | -0.000002 |
| 5,2 | 7 | -0.000065 | -0.000063 | -0.000002 |
| 10,7 | 5 | -0.000171 | -0.000169 | -0.000002 |
| 9,4 | 6 | -0.000112 | -0.000110 | -0.000002 |
| 5,5 | 6 | 0.000256 | 0.000258 | -0.000002 |
| 6,3 | A | -0.000081 | -0.000079 | -0.000002 |
| 9,5 | 6 | -0.000113 | -0.000110 | -0.000002 |
| 5,5 | 2 | 0.000161 | 0.000163 | -0.000002 |
| 4,A | 3 | 0.000024 | 0.000027 | -0.000003 |
| 3,2 | 8 | -0.000174 | -0.000172 | -0.000003 |
| 5,5 | 9 | 0.000063 | 0.000066 | -0.000003 |
| 5,5 | 3 | 0.000184 | 0.000186 | -0.000003 |
| 9,2 | 8 | 0.000316 | 0.000319 | -0.000003 |
| 7,2 | 9 | -0.000051 | -0.000048 | -0.000003 |
| 8,7 | 5 | -0.000153 | -0.000150 | -0.000003 |
| 3,A | 2 | 0.000018 | 0.000020 | -0.000003 |
| 4,2 | 3 | -0.000099 | -0.000096 | -0.000003 |
| 10,10 | 5 | 0.004864 | 0.004868 | -0.000004 |
| 9,3 | 6 | -0.000115 | -0.000111 | -0.000004 |
| 4,3 | 7 | -0.000068 | -0.000063 | -0.000004 |
| 9,5 | 3 | -0.000230 | -0.000225 | -0.000005 |
| 3,2 | 7 | -0.000115 | -0.000110 | -0.000005 |
| 9,7 | 5 | -0.000156 | -0.000151 | -0.000005 |
| 4,A | 9 | -0.000109 | -0.000103 | -0.000006 |
| 9,4 | 3 | -0.000232 | -0.000225 | -0.000007 |
| 2,A | 7 | 0.000104 | 0.000111 | -0.000007 |
| 9,6 | 3 | -0.000233 | -0.000225 | -0.000007 |
| 5,A | 5 | 0.000108 | 0.000115 | -0.000007 |
| 9,8 | 4 | -0.000084 | -0.000077 | -0.000007 |
| A,A | A | 0.000026 | 0.000033 | -0.000007 |
| 6,2 | 6 | 0.000087 | 0.000094 | -0.000008 |
| 9,5 | A | -0.000304 | -0.000297 | -0.000008 |
| 5,A | 3 | 0.000000 | 0.000008 | -0.000008 |
| 9,8 | 3 | -0.000119 | -0.000110 | -0.000008 |
| 9,4 | 2 | -0.000270 | -0.000262 | -0.000008 |
| 4,A | 8 | -0.000034 | -0.000026 | -0.000009 |
| 6,2 | 9 | -0.000201 | -0.000193 | -0.000009 |
| 3,2 | A | -0.000210 | -0.000201 | -0.000009 |
| 3,2 | 9 | -0.000253 | -0.000244 | -0.000009 |
| A,A | 2 | 0.000205 | 0.000214 | -0.000009 |
| 5,A | 2 | -0.000029 | -0.000019 | -0.000009 |
| 4,A | 2 | -0.000010 | 0.000000 | -0.000009 |
| 5,5 | 7 | 0.000169 | 0.000178 | -0.000010 |
| 10,8 | 4 | 0.000594 | 0.000605 | -0.000010 |
| 2,A | 8 | 0.000038 | 0.000048 | -0.000010 |
| 9,7 | 3 | -0.000236 | -0.000226 | -0.000010 |
| 9,9 | 2 | 0.000075 | 0.000086 | -0.000011 |
| 7,5 | 2 | -0.000244 | -0.000233 | -0.000011 |
| A,A | 8 | 0.000147 | 0.000159 | -0.000012 |
| 2,A | 2 | 0.000029 | 0.000041 | -0.000012 |
| 7,2 | A | -0.000092 | -0.000080 | -0.000012 |
| 5,2 | 9 | -0.000274 | -0.000262 | -0.000012 |
| 9,6 | 7 | -0.000351 | -0.000338 | -0.000012 |
| 3,A | 3 | 0.000033 | 0.000045 | -0.000012 |
| 8,6 | A | -0.000310 | -0.000297 | -0.000012 |
| 3,A | 7 | 0.000058 | 0.000071 | -0.000013 |
| 5,5 | 8 | 0.000117 | 0.000129 | -0.000013 |
| 6,2 | A | -0.000181 | -0.000168 | -0.000013 |
| 5,3 | A | -0.000181 | -0.000168 | -0.000013 |
| A,A | 3 | 0.000222 | 0.000235 | -0.000013 |
| 6,3 | 6 | 0.000264 | 0.000277 | -0.000013 |
| A,A | 7 | 0.000196 | 0.000210 | -0.000014 |
| A,A | 5 | 0.000265 | 0.000279 | -0.000014 |
| 8,8 | 5 | 0.000119 | 0.000133 | -0.000015 |
| 10,4 | 6 | -0.000458 | -0.000443 | -0.000015 |
| 5,2 | A | -0.000237 | -0.000222 | -0.000015 |
| A,A | 4 | 0.000242 | 0.000257 | -0.000015 |
| 8,8 | 4 | 0.000082 | 0.000097 | -0.000015 |
| 9,6 | A | -0.000337 | -0.000322 | -0.000015 |
| 7,3 | 3 | 0.000356 | 0.000371 | -0.000015 |
| 5,3 | 9 | -0.000209 | -0.000194 | -0.000016 |
| 5,2 | 8 | -0.000210 | -0.000194 | -0.000016 |
| 5,A | 7 | -0.000023 | -0.000007 | -0.000016 |
| 4,3 | 2 | -0.000118 | -0.000101 | -0.000016 |
| 9,5 | 8 | -0.000357 | -0.000341 | -0.000017 |
| 10,5 | 6 | -0.000459 | -0.000443 | -0.000017 |
| 7,A | 10 | -0.000503 | -0.000486 | -0.000017 |
| 4,2 | 7 | -0.000158 | -0.000141 | -0.000017 |
| 9,4 | 7 | -0.000265 | -0.000247 | -0.000017 |
| 8,2 | 2 | 0.000306 | 0.000324 | -0.000018 |
| 8,4 | A | -0.000262 | -0.000245 | -0.000018 |
| 8,4 | 2 | -0.000251 | -0.000233 | -0.000018 |
| 7,5 | A | -0.000263 | -0.000245 | -0.000018 |
| 5,A | 8 | -0.000081 | -0.000063 | -0.000018 |
| 6,A | 10 | -0.000683 | -0.000665 | -0.000018 |
| 4,2 | A | -0.000236 | -0.000217 | -0.000018 |
| 7,4 | 4 | 0.000496 | 0.000515 | -0.000019 |
| 9,8 | 7 | -0.000119 | -0.000100 | -0.000019 |
| 9,3 | A | -0.000263 | -0.000245 | -0.000019 |
| 8,A | A | 0.000096 | 0.000116 | -0.000020 |
| 4,3 | A | -0.000244 | -0.000223 | -0.000021 |
| 7,2 | 7 | 0.000133 | 0.000154 | -0.000021 |
| 9,8 | 6 | -0.000030 | -0.000008 | -0.000022 |
| 10,4 | 8 | -0.001380 | -0.001358 | -0.000022 |
| 5,A | 9 | -0.000161 | -0.000138 | -0.000022 |
| 9,3 | 2 | -0.000257 | -0.000234 | -0.000023 |
| 9,6 | 8 | -0.000406 | -0.000383 | -0.000024 |
| 4,2 | 9 | -0.000293 | -0.000270 | -0.000024 |
| 10,4 | 9 | -0.001597 | -0.001573 | -0.000024 |
| 10,3 | 6 | -0.000468 | -0.000444 | -0.000024 |
| 7,7 | 6 | 0.000087 | 0.000111 | -0.000024 |
| 4,2 | 8 | -0.000226 | -0.000201 | -0.000025 |
| 4,3 | 8 | -0.000220 | -0.000195 | -0.000025 |
| 8,3 | 10 | 0.000575 | 0.000601 | -0.000026 |
| 10,7 | 3 | -0.000468 | -0.000442 | -0.000026 |
| 8,7 | 6 | -0.000139 | -0.000113 | -0.000026 |
| 8,5 | A | -0.000299 | -0.000273 | -0.000026 |
| 8,6 | 9 | -0.000422 | -0.000396 | -0.000026 |
| 10,8 | 6 | 0.000784 | 0.000811 | -0.000026 |
| A,A | 6 | 0.000274 | 0.000300 | -0.000027 |
| 9,9 | 5 | 0.000147 | 0.000174 | -0.000028 |
| 9,9 | 8 | 0.000075 | 0.000103 | -0.000028 |
| 7,2 | 10 | -0.000546 | -0.000518 | -0.000028 |
| 9,7 | 6 | -0.000142 | -0.000114 | -0.000028 |
| 9,4 | 8 | -0.000327 | -0.000298 | -0.000029 |
| A,A | 10 | 0.000270 | 0.000299 | -0.000029 |
| 4,3 | 9 | -0.000293 | -0.000264 | -0.000029 |
| 7,6 | A | -0.000303 | -0.000274 | -0.000029 |
| 4,A | 10 | -0.000618 | -0.000588 | -0.000030 |
| 9,9 | 4 | 0.000111 | 0.000142 | -0.000031 |
| 10,5 | 3 | -0.000934 | -0.000903 | -0.000032 |
| 8,8 | 7 | 0.000110 | 0.000142 | -0.000032 |
| 9,9 | 7 | 0.000145 | 0.000177 | -0.000032 |
| 3,2 | 10 | -0.001091 | -0.001059 | -0.000033 |
| 7,3 | 7 | 0.000322 | 0.000355 | -0.000033 |
| 6,A | 6 | 0.000191 | 0.000223 | -0.000033 |
| 9,9 | 3 | 0.000078 | 0.000112 | -0.000033 |
| 10,2 | 6 | -0.000479 | -0.000445 | -0.000033 |
| 9,5 | 10 | -0.001607 | -0.001572 | -0.000034 |
| 8,4 | 7 | -0.000237 | -0.000199 | -0.000038 |
| 9,5 | 7 | -0.000336 | -0.000297 | -0.000039 |
| 10,2 | 7 | -0.000819 | -0.000780 | -0.000039 |
| 8,6 | 7 | -0.000336 | -0.000297 | -0.000039 |
| 6,4 | 6 | 0.000472 | 0.000511 | -0.000039 |
| 8,8 | 6 | 0.000127 | 0.000167 | -0.000040 |
| 9,3 | 7 | -0.000239 | -0.000199 | -0.000040 |
| 8,3 | 3 | 0.000427 | 0.000467 | -0.000040 |
| 10,6 | 3 | -0.000944 | -0.000904 | -0.000040 |
| 8,5 | 9 | -0.000398 | -0.000358 | -0.000040 |
| 8,2 | 8 | 0.000213 | 0.000255 | -0.000042 |
| 6,2 | 10 | -0.000887 | -0.000844 | -0.000042 |
| 10,3 | A | -0.001128 | -0.001085 | -0.000043 |
| 6,6 | 6 | 0.000036 | 0.000079 | -0.000043 |
| 10,4 | 3 | -0.000947 | -0.000904 | -0.000043 |
| 9,2 | 2 | 0.000380 | 0.000423 | -0.000043 |
| 10,7 | A | -0.001350 | -0.001306 | -0.000044 |
| 10,2 | A | -0.001018 | -0.000974 | -0.000044 |
| 10,6 | A | -0.001417 | -0.001373 | -0.000044 |
| 5,3 | 10 | -0.000889 | -0.000844 | -0.000045 |
| 7,6 | 9 | -0.000404 | -0.000358 | -0.000046 |
| 9,2 | 9 | 0.000155 | 0.000201 | -0.000046 |
| 10,7 | 2 | -0.000622 | -0.000576 | -0.000046 |
| 9,3 | 8 | -0.000305 | -0.000254 | -0.000051 |
| 6,5 | 6 | 0.000549 | 0.000601 | -0.000052 |
| 10,5 | 7 | -0.001407 | -0.001354 | -0.000054 |
| 9,9 | 6 | 0.000148 | 0.000202 | -0.000054 |
| 7,5 | 8 | -0.000310 | -0.000254 | -0.000056 |
| 10,3 | 7 | -0.001044 | -0.000987 | -0.000057 |
| 10,7 | 9 | -0.001607 | -0.001549 | -0.000057 |
| 10,5 | 2 | -0.001110 | -0.001052 | -0.000058 |
| 7,A | 7 | 0.000298 | 0.000356 | -0.000058 |
| 7,5 | 9 | -0.000376 | -0.000317 | -0.000059 |
| 5,2 | 10 | -0.001142 | -0.001081 | -0.000061 |
| 7,4 | 7 | 0.000353 | 0.000414 | -0.000061 |
| 8,4 | 9 | -0.000380 | -0.000318 | -0.000062 |
| 10,2 | 8 | -0.001060 | -0.000997 | -0.000063 |
| 8,5 | 7 | -0.000316 | -0.000253 | -0.000063 |
| 10,4 | A | -0.001256 | -0.001191 | -0.000065 |
| 9,A | A | 0.000305 | 0.000371 | -0.000066 |
| 10,6 | 2 | -0.001121 | -0.001053 | -0.000068 |
| 8,3 | 8 | 0.000239 | 0.000309 | -0.000070 |
| 8,6 | 10 | -0.001648 | -0.001577 | -0.000071 |
| 7,5 | 10 | -0.001364 | -0.001291 | -0.000073 |
| 7,6 | 8 | -0.000381 | -0.000304 | -0.000076 |
| 8,4 | 10 | -0.001368 | -0.001291 | -0.000077 |
| 4,2 | 10 | -0.001224 | -0.001146 | -0.000077 |
| 10,3 | 8 | -0.001267 | -0.001189 | -0.000078 |
| 10,8 | 9 | -0.000757 | -0.000677 | -0.000080 |
| 10,2 | 9 | -0.001330 | -0.001249 | -0.000081 |
| 10,10 | 8 | 0.005671 | 0.005755 | -0.000085 |
| 10,5 | 8 | -0.001614 | -0.001529 | -0.000085 |
| 10,10 | 7 | 0.005536 | 0.005621 | -0.000085 |
| 10,7 | 6 | -0.000118 | -0.000033 | -0.000085 |
| 9,3 | 10 | -0.001378 | -0.001293 | -0.000085 |
| 9,2 | 10 | 0.000506 | 0.000593 | -0.000087 |
| 8,A | 8 | 0.000440 | 0.000529 | -0.000089 |
| 10,10 | 6 | 0.004838 | 0.004927 | -0.000089 |
| 10,8 | 8 | 0.000277 | 0.000371 | -0.000095 |
| 5,5 | 5 | 0.000126 | 0.000222 | -0.000096 |
| 9,6 | 10 | -0.001808 | -0.001709 | -0.000099 |
| 5,A | 10 | -0.000810 | -0.000711 | -0.000099 |
| 4,3 | 10 | -0.001187 | -0.001086 | -0.000101 |
| 10,5 | 9 | -0.001835 | -0.001731 | -0.000104 |
| 10,10 | 2 | 0.004503 | 0.004610 | -0.000108 |
| 10,10 | 3 | 0.004577 | 0.004689 | -0.000111 |
| 10,5 | A | -0.001404 | -0.001292 | -0.000111 |
| 10,7 | 8 | -0.001522 | -0.001407 | -0.000115 |
| 10,4 | 2 | -0.001174 | -0.001058 | -0.000116 |
| 10,3 | 2 | -0.001177 | -0.001059 | -0.000119 |
| 9,A | 9 | 0.000554 | 0.000674 | -0.000120 |
| 10,10 | 9 | 0.005386 | 0.005507 | -0.000121 |
| 10,10 | 4 | 0.004635 | 0.004767 | -0.000132 |
| 10,4 | 7 | -0.001321 | -0.001187 | -0.000134 |
| 8,5 | 10 | -0.001583 | -0.001447 | -0.000135 |
| 7,6 | 10 | -0.001597 | -0.001449 | -0.000148 |
| 10,9 | 9 | 0.000765 | 0.001012 | -0.000247 |
| 10,A | A | 0.003014 | 0.003691 | -0.000677 |
| 10,10 | 10 | 0.013570 | 0.014752 | -0.001181 |
I'm thinking of making a table that considers just the total of the player's initial hand and based on simulation results.
Quote: Ace2https://wizardofodds.com/games/blackjack/player-expected-return/
Thanks for pointing that out - I had never found it. I'm not crazy about it being infinite deck, and the colors and graphical format are very dated.
In my previous post I was speaking from the heart because I believe the appearance and content of WOO could be improved to make it more attractive and interesting (its not my site but I do care about it and I think it has great bones). That table should be brought up to modern graphical standards and made more "central" or at least easier to find.
Quote: WizardThis table lists the expected value of all 650 for both one and eight decks under the same rules as my simulation. The values are taken from these expected value tables:
Blackjack expected Returns for one deck and dealer hits on soft 17 and
https://wizardofodds.com/games/blackjack/appendix/9/8dh17r4/
Unlike my simulation study, these tables assume perfect combinatorial strategy at every decision point. This helps in single deck much more than eight decks.
The expected value columns are the product of the expected value of the given situation and the probability of it happening. It is listed in order of the expected value difference, in order of what is best for the player in a single-deck game.
Note: TABLE DELETED for the sake of brevity
I'm thinking of making a table that considers just the total of the player's initial hand and based on simulation results.
MAGNIFICENT! Personally, I love it! Its something new on a topic (Blackjack) that has been very worked over, and its interesting. I may not be your average WOO user, but I think its great!
Edit: If you make a table based on players hand total, I think you may be throwing out the baby with the bathwater. A T,3 vs T will be very different than a 9,4 vs T and a 7-6 is always different than T-3. Indeed, T-3 vs T and 7-6 vs T are at polar opposite ends of the table.
Quote: gordonm888Thanks for pointing that out - I had never found it. I'm not crazy about it being infinite deck, and the colors and graphical format are very dated.
It's not infinite deck. I have tables for 1, 2, 4, 5, 6, and 8 decks, both H17 and S17.
Quote:In my previous post I was speaking from the heart because I believe the appearance and content of WOO could be improved to make it more attractive and interesting (its not my site but I do care about it and I think it has great bones). That table should be brought up to modern graphical standards and made more "central" or at least easier to find.
I agree that some things, like those tables, are hard to find. I started the site in straight HTML in 1997 and elements of that lack of organization remain to this day. For example, those EV tables are titled as "appendices" in the URL. What other site has appendices? The whole thing was held together by Duck Tape when I sold it.
I'm clearly not very good with appearances. I would suggest you bounce any aesthetic (hard word to spell) suggestions off of Zuga.
Similarly, Red means that 8 decks gives a higher return and the darker reds correspond to a larger difference between 8 deck return and 1 deck return.
Green means that Wizard's table showed a zero for the difference between 1 deck and 8 deck return.

I think the most important feature to look for is the basic change between red and blue, because they represent a sign difference.
Wizard, I hope this helps!
Quote: odiousgambitOne thing I've been wondering about lately is if it is true or not that not only the HE gets better for the player when there are fewer decks, but the variance also increases, and increase is desirable in BJ, I have always felt. I get the sense increased variance with fewer decks is true, but as we know gut feelings can mislead. Anybody know?
What makes you think that an increase in variance is desirable in blackjack? One of the reasons casinos continue to offer games of blackjack that can be beat is because they know that because the majority of players, will be under funded, and that very variance will eventually get them.
That is sort of my 2020 in a nutshell. I play at a level that my normal max bet is just below the critical $500 threshold, because that is a level pretty well tolerated by the casinos I play. So when casinos reopened after the shutdown, I wanted to more quickly build EV, to "recoup" for lost time, so I doubled my playing stakes, now max betting just under the next critical threshold of $1000.
I figured I could get away with this, at least short-term, because casino personnel would be busy with other new responsibilities related to covid. Making sure new maximum number of players, wiping down each spot after a player leaves, enforcing mask wearing. Those kind of added new responsibilities of pit folks. Surveillance also had to be on the look out for covid related things. People playing too close together, and mask enforcement.
So that part worked well. I was able to play higher stakes without drawing much extra attention for 3 or 4 months until people settled into their new roles. The problem for me was over that rather short time of 3-4 months, playing the best games I could, double deck, at my new higher stakes, variance just wasn't kind to me over that short run. I went into the red and stayed there for most of that time, just climbing slightly into the black at the end, but still significantly below expectation or EV. Has I been able to play my normal amount for a year, I have no doubt my results would have been closer to expectation as they always have for 17 years now. But this year that smaller sample size at higher stakes, variance just happened to bite me in the ass. So this was a case where variance was not my friend.
before reading further, let me point out I should have said "desirable for someone who flatbets". If you have a player's edge from card counting and varying your bet, you don't want more variance, agreed.Quote: kewljWhat makes you think that an increase in variance is desirable in blackjack?
I disagree here, it's the HE that gets them, not variance. If there was no variance at all, the player could *literally* never win. As it is, seems like with 8 decks the house just keeps winning every session, with not enough variance to win once in a while.Quote:One of the reasons casinos continue to offer games of blackjack that can be beat is because they know that because the majority of players, will be under funded, and that very variance will eventually get them.
Again, I'm well aware that APs have no reason to want more variance.Quote:That is sort of my 2020 in a nutshell.... [snip]
Quote: gordonm888Here is a color-coded chart for the difference in returns between 1 deck and 8 deck BJ using numbers from Wizard's table.
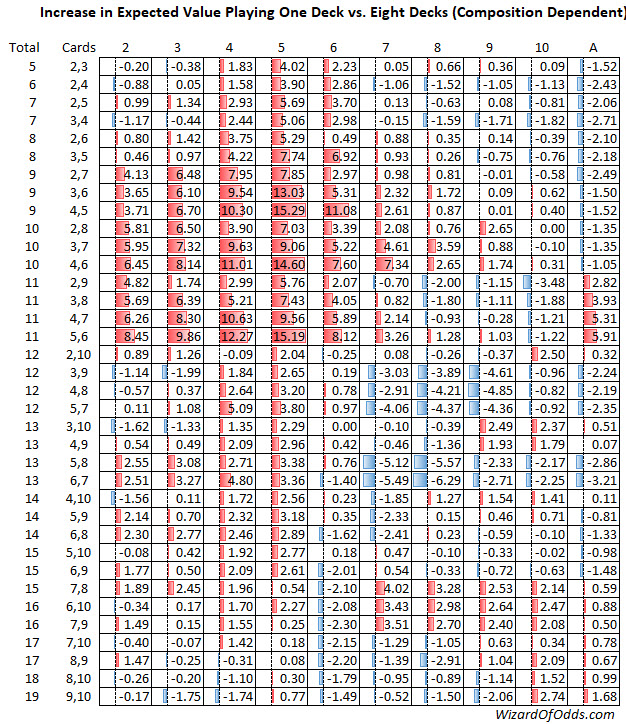
Thank you! This is good stuff. I hope you will appreciate the following similar table. I know you like to break down the starting hand by composition, which I may do next. However, I think the reader may see what is going on more clearly if the table is total dependent.
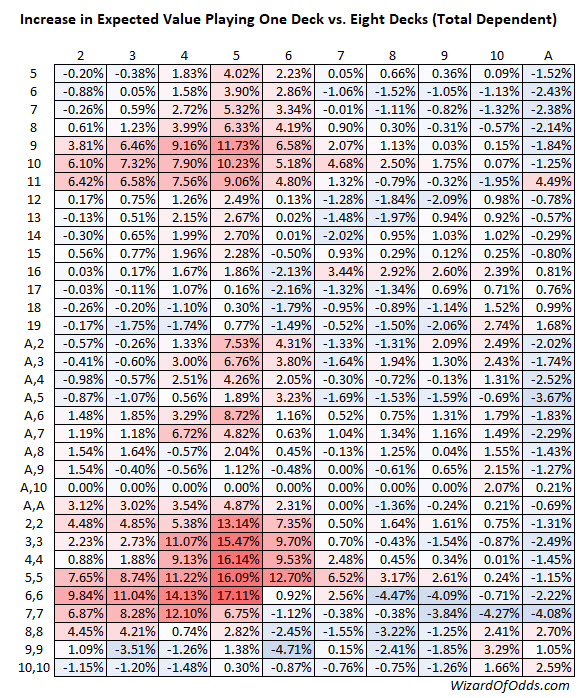
Red cells are good for the player in a single-deck game and blue cells are bad.
The main thing that jumped out at me is the significance of fives. This table makes fives look awful for the player. Removing just one of them in the single-deck game, as evidenced by a dealer 5, is extremely helpful to the player. Of course, it doesn't make much difference in an eight-deck game.
Quote: kewljWhat makes you think that an increase in variance is desirable in blackjack? One of the reasons casinos continue to offer games of blackjack that can be beat is because they know that because the majority of players, will be under funded, and that very variance will eventually get them.
I disagree.
The way this issue is often expressed is in the following question:
If a casino offered a game with exactly 0% house edge, who would come out ahead in the long run?
A. The casino
B. The players
C. Neither. The net casino profit (on a percentage basis) will always hover close to zero.
The answer is C.
Since this is getting a bit off topic, I'll split this off there seems to be further discussion about it.
Quote: WizardI disagree.
The way this issue is often expressed is in the following question:
If a casino offered a game with exactly 0% house edge, who would come out ahead in the long run?
A. The casino
B. The players
C. Neither. The net casino profit (on a percentage basis) will always hover close to zero.
The answer is C.
Since this is getting a bit off topic, I'll split this off there seems to be further discussion about it.
C is of course the mathematical answer. If enough people reply to warrant a split I do have one thought.
It seems to me that most of the time on slots unless a person makes a big win they burn off any winnings. In "Super Casino" they talked about how a property (Circus Circus! maybe but I forget and it does not matter) bumped their payouts just a touch. Coin in went up as players noticed the better payouts. But hold went up because they said IIRC about 90% of the increased wins just got spun off, it never hit the door.
How close to 0% could a slot get and still make an acceptable profit? Could you even make it 0% but goose the variance such that even if a player gets a few wins they do not win enough that they want to cash but rather just spin the win off?
FWIW I do remember some Vegas show on some cable channel showed a bank of slots with at least one machine returning >100%. Yeah, I know that is more marketing than anything else, but just to say it has been tried.
Anyone still doubting it, take it up with the Wizard, whose page here shows BJ to have a standard deviation of just 1.15*
https://wizardofodds.com/gambling/house-edge/
* with these rules, "Dealer stands on soft 17, player may double on any two cards, player may double after splitting, resplit aces, late surrender". Does not mention the number of decks, which I am really wondering about now, as to the effect on variance
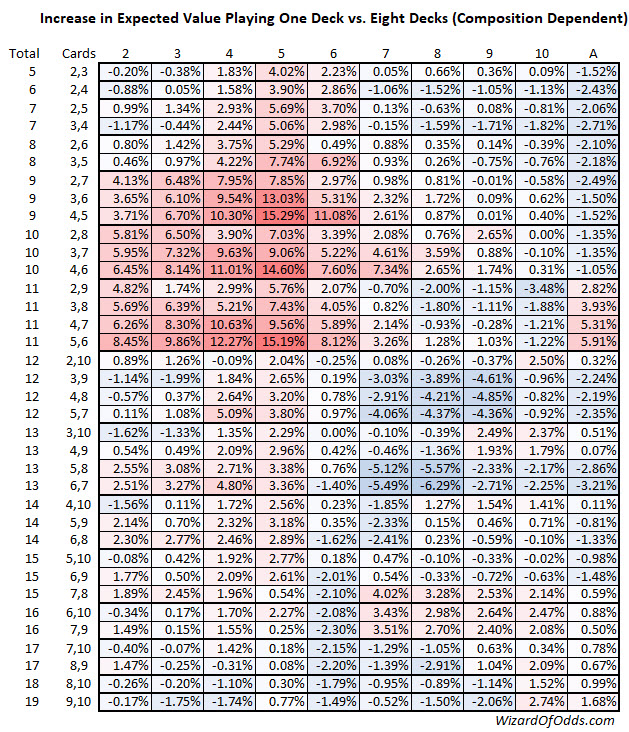
Quote: WizardHere is a new table shows the increase in expected value playing single-deck vs. eight-deck. This one differs from the previous one is I break down the hard hands by composition.

My suggestions would be:
1. delete the % sign from each cell, and put a title on it that the numbers are in percent. Keep the level of precision as it is now, so that the result is a cleaner looking table.
2. Given the use of numbers in the cells (which I like and was going to do myself, but was too lazy) I would suggest that you forego the use of shaded colors, and simply use two colors to show positive and negative.
- alternatively, maybe use a third color or shaded color, to show ΔEV values that are either very large or near zero. The very light reds and blues are too subtle, IMO.
Oh, it's a CSM.
Quote: gordonm888My suggestions would be:
1. delete the % sign from each cell, and put a title on it that the numbers are in percent. Keep the level of precision as it is now, so that the result is a cleaner looking table.
Good suggestion, thanks.
Quote:2. Given the use of numbers in the cells (which I like and was going to do myself, but was too lazy) I would suggest that you forego the use of shaded colors, and simply use two colors to show positive and negative.
- alternatively, maybe use a third color or shaded color, to show ΔEV values that are either very large or near zero. The very light reds and blues are too subtle, IMO.
You make a valid complaint about most of the cells being too faint. I wanted neutral (no change in EV) to be while, which is why the blues are so faint. However, I personally like tables that are shaded. It let's the reader quickly grasp what is going on. Maybe I'll use color bars. Let me think about it...
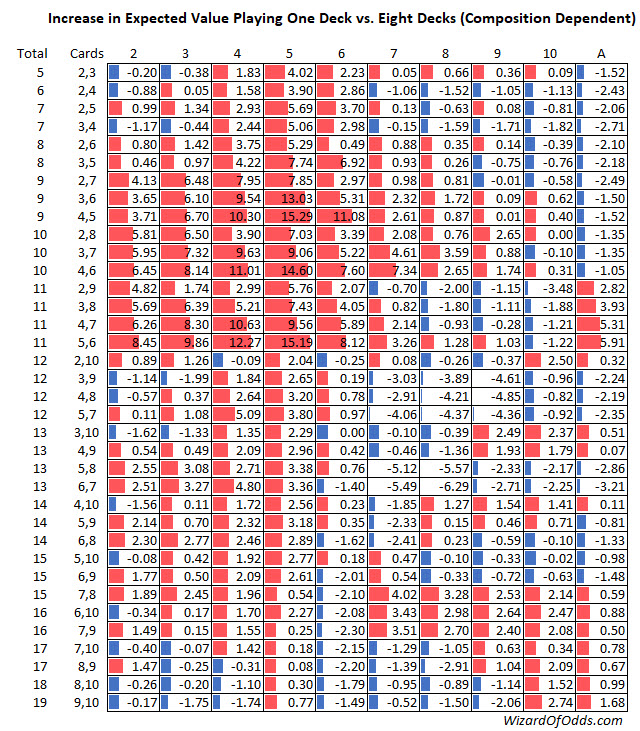
At least my table making skills are improving.
Quote: ChumpChangeAt P3,10 vs. D6 the 0.00 has a blue bar and P6,7 vs. D7 the -5.49 has no discernable blue bar. Shouldn't larger negative numbers have larger bars and 0 have no bar? Seems backwards on the negative side.
Good catch. Please consider this "version 3."
I'd like to submit this to any serious gaming journals/publications if anyone knows of any.
Oh, stop.Quote: WizardThis is my proudest work in a long time (which will probably mean that nobody will read it)
But read it and comment? That means you have something to contribute. If the reader does not qualify to be a wizard, he risks sounding foolish. I've just started and probably don't have anything to contribute, but just to show you I'm reading, I'll comment.
This puts it well, I now understand it better than when you made this point before. It's still amazing to me the effect of what would seem like 'not mattering much' in gambling.Quote:... hitting generally takes place with hands that have smaller than average-value cards. This removal of small cards in hitting situations causes the remaining cards to have a surplus of high ones. This effect of removal of the small cards before the bust is more significant in a single-deck game
Still reading stay tuned.
Quote: WizardI'm proud to announce that my page on Why the number of decks matter in blackjack. This is my proudest work in a long time (which will probably mean that nobody will read it) so I would appreciate any comments..
I was taking to a friend a few months ago and this topic came up. His point was “the ratio of the cards is the same in 1 deck vs 8 decks”. That is, off the top, 1 out of 13 cards is an Ace, etc, no matter the number of decks. Honestly I’ve had the same thought and didn’t have a great answer for him. I’ll read this and try to wrap my head around the math answer for why # decks affects house edge
Quote: TinManI was taking to a friend a few months ago and this topic came up. His point was “the ratio of the cards is the same in 1 deck vs 8 decks”. That is, off the top, 1 out of 13 cards is an Ace, etc, no matter the number of decks. Honestly I’ve had the same thought and didn’t have a great answer for him. I’ll read this and try to wrap my head around the math answer for why # decks affects house edge
That's true, the first card has a 1/13 of being any given rank. However, the second card has a 1/17 of being the same in single deck and 1/13.4 in an eight-deck game.
It does seem you do a lot more doubling down and splitting with one deck vs. 8 decks.
https://wizardofodds.com/games/blackjack/strategy/calculator/
Quote: ChumpChangeI keep looking all over the internet for these handy dandy Basic Strategy Cards. I just found a couple in your post. But I probably need more for 2 decks, 4 decks, 6 decks, not to mention the changes in strategy based on the true count for the 5 different deck strategies.
It does seem you do a lot more doubling down and splitting with one deck vs. 8 decks.
Before my last Vegas trip, I printed out in color BS charts for 1,2,4-8 decks from WOO BS generator. Had versions with surrender and no surr. H17 and S17 for all but the single deck game. Laminated them double sided so each card has the surr and no surr charts. Total of 10 charts. Really handy. Obviously none of this captures true count adjustments just BS. I’d been meaning to do it for awhile.
Quote: WizardThat is one of the essences of a well-designed casino game -- the player doesn't see where the house has the advantage. In blackjack and most poker games it is a player positional disadvantage. The idea to remove the 10's in Spanish 21 was also a good one.
I get asked from time to time by the other side about how to significantly increase the house edge, like by 1%, in blackjack without changing the 3-2 payoff, mandating a side bet, charging a commission on wins, nor change the deck composition in a way the average player won't notice. Nothing good has ever come to mind.
I couldn't agree more with you about having a house edge that isn't obvious to the players. Not to brag but I like to think my biggest accomplishment with my game "Cards vs Dice" is the fact that it took you > 5 minutes to determine the game's house edge. There were a couple of minutes where I swear you were convinced there wasn't a house edge & that I had lost my mind lol.
Quote: Wizard
Second, it's always been my policy to teach to near the top. If you put everybody on the bell curve, I try to aim at the person about one standard deviation above average (meaning 84% are less intelligent and 16% are more). There are already plenty of advanced books for those 2 or 3 standard deviations above the norm and plenty of sources for those who need things simplified as much as possible. I aim for those in between.
I like this strategy. Might just have to borrow it for my 1st published book, whenever I get to complete it ;) So I'm assuming the target IQ level is 110-120 since you say "aim at the person about one standard deviation" so I'm assuming "about" means that they are almost or slightly above the 2nd standard deviation. I have trouble imagining this since I don't know my IQ to compare with. Your average human doesn't seem that intelligent to me but then again I don't care to teach the average person, but I also don't want only the brightest minds being able to contribute to my discussions since it could take forever to find someone that can contribute.
I like your solution but I find it hard for me to implement it, any suggestions on how to help? I know communication isn't my strong point but dumbing down my communication to its simplest form just doesn't seem to work either :/
But isn't it just as likely that the dealer gets the first natural? I don't get how this applies until we know who gets the first .Quote:... the reason the probability of getting the ace is higher in the single-deck game is the deck is richer in aces after you remove a 10 from it. The same is true if the first card is an ace; the remaining cards will be richer in tens in the single-deck game.
Furthermore, if the player does get a blackjack, the probability of the dealer’s getting one goes down as the number of decks goes down.
this is well known, but is in effect without regard to who gets one first, so it doesn't seem like the entire answer.Quote:... The player wins an extra half unit with every winning blackjack.
Quote: odiousgambitBut isn't it just as likely that the dealer gets the first natural? I don't get how this applies until we know who gets the first .
this is well known, but is in effect without regard to who gets one first, so it doesn't seem like the entire answer.
I am not clear about the point that you are making here.
Consider a heads up game with a five-card deck composed of four tens and a single ace. Dealer and player will always stand because they will always have a 20 or BJ in the first two cards. Whenever dealer or player gets a BJ, they will get it first. There is only one BJ possible on each hand.
One fifth of the time, they will push with each having 20. 40% of the time, dealer will have BJ and 40% of the time, the player will have BJ. The player will win a full unit every five hands, on average.
Now take out a ten, and the player wins a full bet every 4 hands, on average.
OK, thanks, I guess the point you are making is that in a game rich in tens and in which BJ is possible once, though equally likely to go to player or dealer, it is always good for the player and sometimes 'really good'?Quote: MentalI am not clear about the point that you are making here.
Consider a heads up game with a five-card deck composed of four tens and a single ace. Dealer and player will always stand because they will always have a 20 or BJ in the first two cards. Whenever dealer or player gets a BJ, they will get it first. There is only one BJ possible on each hand.
One fifth of the time, they will push with each having 20. 40% of the time, dealer will have BJ and 40% of the time, the player will have BJ. The player will win a full unit every five hands, on average.
Now take out a ten, and the player wins a full bet every 4 hands, on average.
Likewise fewer decks are good for the player, sometimes really good, and it averages out so you can make a statement about what the HE is for one deck, two, etc and compare them.
The Wizard can decide if he wants to try to clarify, it's not obvious what he means in this section
Quote: odiousgambitOK, thanks, I guess the point you are making is that in a game rich in tens and in which BJ is possible once, though equally likely to go to player or dealer, it is always good for the player and sometimes 'really good'?
Likewise fewer decks are good for the player, sometimes really good, and it averages out so you can make a statement about what the HE is for one deck, two, etc and compare them.
My point is this: In the case where the dealer gets the BJ, it does hurt the chances for the player to get BJ. In fact, it extinguishes any chance. I thought this might have been the point you were asking about.
But, the reverse is true, as well. If the player gets a BJ, the dealer is shut out. In a 8-deck shoe game, the dealers chances of getting a BJ is hardly affected by me getting a BJ. In the four-card game, the probability goes from 100% to 0%. These correlation affects are always stronger the smaller the number of cards in play.
Quote: USpapergamesI couldn't agree more with you about having a house edge that isn't obvious to the players. Not to brag but I like to think my biggest accomplishment with my game "Cards vs Dice" is the fact that it took you > 5 minutes to determine the game's house edge. There were a couple of minutes where I swear you were convinced there wasn't a house edge & that I had lost my mind lol.
Yes, I recall that, but not the details. Was it a player positional disadvantage as well?


