Thread Rating:
I'm not as mathematically inclined, so I was wondering if you could comment on my thought process so far. If this has been answered before or is in the wrong place in the forum, I'd appreciate if you could forward me to the right place. Anyways, here it goes: assuming I'm not counting cards and only playing basic strategy, I understand that in the long-run I lose money as my EV is lower than my bet. However, it also means that my returns vary in the short-run, above and below the EV. Does that mean that I could exit on a positive variance and enjoy my winnings and, assuming I have sufficient bankroll, play through a negative variance until I converge back to the mean (or reach a positive variance again)? If this thought process is correct, is it an effective way to enjoy the game and is there a "standard" suggested bankroll?
Appreciate any comments!
Quote: saliatDoes that mean that I could exit on a positive variance and enjoy my winnings and, assuming I have sufficient bankroll, play through a negative variance until I converge back to the mean (or reach a positive variance again)? If this thought process is correct, is it an effective way to enjoy the game and is there a "standard" suggested bankroll?
Yes, you can quit when you're ahead and enjoy your winnings.
With a big enough bankroll, you might be able to ride out a losing streak and catch up.
I see lots of people playing and enjoying themselves while essentially flat betting.
8 units session bankroll is too small. 20 seems to be pretty typical.
If you want noticeable comps, you might consider playing more than table minimum... like $25 a hand on a $5 table.
Quote: saliatAnyways, here it goes: assuming I'm not counting cards and only playing basic strategy, I understand that in the long-run I lose money as my EV is lower than my bet. However, it also means that my returns vary in the short-run, above and below the EV. Does that mean that I could exit on a positive variance and enjoy my winnings and, assuming I have sufficient bankroll, play through a negative variance until I converge back to the mean (or reach a positive variance again)?
You "could", but probability and statistics don't work that way.
First of all, there is no guarantee that you will "lose money in the long run"; that's just what is expected to happen. When you throw two dice, seven is expected to come up 1/6 of the time, but that doesn't mean that you won't throw 27 sevens in a row. There's a saying; "The race is not always to the swift, nor the battle to the strong, but that's the way to bet."
Second, if "things always even out in the end", then why not do this:
(a) If you lose money, keep playing until you get back even;
(b) If you win money, switch to a different table where you "start over again" in terms of wins and losses?
The reason you don't is, it doesn't work that way...and even if it did, how do you know that the game had not been "running positive" for the three hours before you got to the table and is "due to even out" with a run of losses?
You "enjoy the game" by playing each hand as if it was your first, and forget what happened in the past (well, unless you're a card counter, but even then, forget everything that happened before the most recent shuffle).
Quote: saliatHi,
is it an effective way to enjoy the game and is there a "standard" suggested bankroll?
Appreciate any comments!
Whatever your little heart desires that you are comfortable with. IMHO. Don't listen to other people, there are tons of formulas going around of course.
Quote: saliatHi,
I'm not as mathematically inclined, so I was wondering if you could comment on my thought process so far. If this has been answered before or is in the wrong place in the forum, I'd appreciate if you could forward me to the right place. Anyways, here it goes: assuming I'm not counting cards and only playing basic strategy, I understand that in the long-run I lose money as my EV is lower than my bet. However, it also means that my returns vary in the short-run, above and below the EV. Does that mean that I could exit on a positive variance and enjoy my winnings and, assuming I have sufficient bankroll, play through a negative variance until I converge back to the mean (or reach a positive variance again)? If this thought process is correct, is it an effective way to enjoy the game and is there a "standard" suggested bankroll?
Appreciate any comments!
saliat,
You made 2 ID's, and everyone is only allowed one. Possibly there was something in your sign-up that went wrong and you made the second ID, so instead of banning you I just killed the duplicate. Please don't make any more ID's; just use this one.
As to your question, in my opinion as a fellow non-counter, I think you should play your best game and enjoy yourself. Over the long term, yes, you're playing a -EV game. They all are, but I still enjoy playing them. No reason you can't be a lifetime winner. But the cards have no memory, so without counting and betting accordingly, there's no reason to think you will "recover" from any trend, good or bad, and you shouldn't expect that you're due for winning or losing based on the math. The -EV numbers are calculated using more hands than nearly anybody will play in a lifetime, so your personal experience can vary widely from that expectation. They're more for a casino dealing a game 24/7/365 to estimate their exposure with many tables and players than for any one person to have exactly those results.
Quote: saliatAppreciate any comments!
If I understand you right, the short answer is no. If you play a -EV game and win, I'd suggest you walk away for life, a winner. I'm up about $600 on -EV games that I played sporadically when I was kind of down. I haven't played for years and have no plans to in the future.
If the process of playing a -EV game is enjoyable to you, don't over think things, just accept that you're going to lose $ in the long run, and set aside what you're willing to lose for the sake of entertainment.
Quote: MidwestAPThere is not a way to 'play through a negative variance' as the same house edge still applies.
Eh, I don't think he means "play through the variance" like a counter would... Meaning he's waiting for the "mathematical" upswing towards his EV. He's counting on variance to give him an opportunity to be "up" at a given point, knowing that if he keeps playing it will eventually move downwards towards his overall EV.
Quote: ThatDonGuyYou "could", but probability and statistics don't work that way.
First of all, there is no guarantee that you will "lose money in the long run"; that's just what is expected to happen. When you throw two dice, seven is expected to come up 1/6 of the time, but that doesn't mean that you won't throw 27 sevens in a row. There's a saying; "The race is not always to the swift, nor the battle to the strong, but that's the way to bet."
Second, if "things always even out in the end", then why not do this:
(a) If you lose money, keep playing until you get back even;
(b) If you win money, switch to a different table where you "start over again" in terms of wins and losses?
The reason you don't is, it doesn't work that way...and even if it did, how do you know that the game had not been "running positive" for the three hours before you got to the table and is "due to even out" with a run of losses?
You "enjoy the game" by playing each hand as if it was your first, and forget what happened in the past (well, unless you're a card counter, but even then, forget everything that happened before the most recent shuffle).
Not sure if you had some sarcasm to it or not, but (b) is flawed. It doesn't matter what table you're at, what day it is, etc... What matters is what bankroll you're playing from. If 1 persons lifetime can be looked at as "their" bankroll... Then it will gravitate towards EV no matter the table, day, casino, etc
Quote: saliatHi,
I'm not as mathematically inclined, so I was wondering if you could comment on my thought process so far. If this has been answered before or is in the wrong place in the forum, I'd appreciate if you could forward me to the right place. Anyways, here it goes: assuming I'm not counting cards and only playing basic strategy, I understand that in the long-run I lose money as my EV is lower than my bet. However, it also means that my returns vary in the short-run, above and below the EV. Does that mean that I could exit on a positive variance and enjoy my winnings and, assuming I have sufficient bankroll, play through a negative variance until I converge back to the mean (or reach a positive variance again)? If this thought process is correct, is it an effective way to enjoy the game and is there a "standard" suggested bankroll?
Appreciate any comments!
Hi saliat, and welcome to the forums. You'll find many intelligent people here, math based or not =). I believe I understand your question(s). Please refer to my graph below (sorry it's hacky and in MS Paint, but it should do the trick):
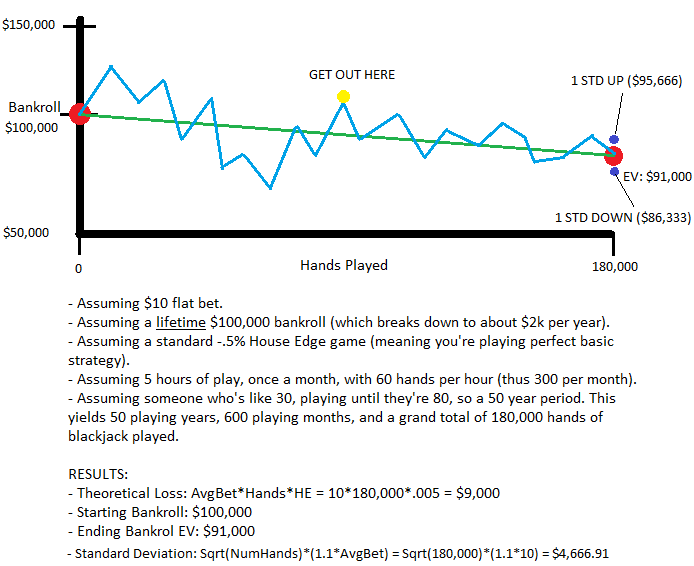
*Blue Line = A random example of how you might expect ones bankroll to fluctuate over time (starting off changing a lot, but dampening down and dancing around the line of best fit towards the long run and approaching EV).
*Green Line = Expected Value at that given number of hands.. Thus, half way through (90k hands) you could expect to be at that spot on the green line, give or take your standard deviation)
*Red Dots = Starting/Ending bankroll.
*Purple Dots = Your potential ending bankroll taking standard deviations in to account.
*Gold Dot = An example of playing for 20-25 years then choosing to exit the game while you're on a fortunate variance upswing from your EV (and actually "up" on your bankroll). Note: This may or may not happen pending the variance discussed later.
If I understand you correctly, you're asking if you can play FOR the variance of the game, and then choose to get out while you're up. Also, you're asking if you have poor variance (on your non counting EV), then you'd expect to come back up to your EV (even if it's negative from non counting). This is absolutely correct. In the graph above you have an example of a basic strategy player. Their EV over the long run is -$9,000. Thus, if in the first 5 years of play (playing absolutely perfect basic strategy) they are down $20,000... Then yes, you could 'expect' to move back towards your EV (thus you should expect as you get closer to 'the long run' to win more money). Do not confuse this with actually winning though. This just means you'll go from -$20k, to -$10k, and ultimately to your -$9k EV. This also doesn't mean in the short term that you couldn't go down even more! Just that by the time the player above hits 180,000 hands he should only be down $9,000... So eventually we would expect to see a move from something like -$20k upwards towards this EV.
To answer your other question of "could you ever play for the variance, then just quit while you're ahead?" Yes, you can... HOWEVER... Variance is just that, variance. You have no idea or way of knowing if it will take you up or down. You might start with $100,000, and end up being down your exact EV (-$9,000), but you might NEVER be up. You might lose $50k in the first 10 years, then spend the next 40 years getting back to your EV of -$9k. On the flip side of the coin, you might win $50k in your first 10 years, then spend the next 40 years giving it all back until you hit your inevitable EV of -$9k.
Now, in general we'd expect variance to dance around the "line of best fit", or your "EV" at any given number of hands (the green line above). This will often be within a standard deviation or two from the green line. What I mean by that is, pick a point on the image along the green line... At any given time (number of hands) you could "expect" to be at that point, or slightly above/below given the standard deviation (which is described how to calculate above).
Results
You can 'play through the variance' to eventually get to your EV. This may mean being up, or down. In general we would expect both to happen on the journey to your end EV, however this is not guaranteed. As stated above, you might have poor luck and just ALWAYS be down the entire time. On the flip side you could always be up the entire time, drifting downwards towards your EV as you hit the long run.
My personal opinion is that you could play for a decade or two, enjoying the game, comps, etc, but you must know that at some point you need to either exit while you're "up", never playing the game again, or accept the fact that you will inevitably be down.
If you'd like me to suggest a bankroll, you'll need to provide more information, such as your average bet. It would help to know if you're a flat better (only bet 1 amount all the time) or if you still spread your bet (start at $10, but when you 'feel' it you might bet $100). I hope you found this information useful, and don't hesitate to ask about anything I may not have explained well enough.
Again, welcome to the forums =).
Quote: RomesNot sure if you had some sarcasm to it or not, but (b) is flawed. It doesn't matter what table you're at, what day it is, etc... What matters is what bankroll you're playing from. If 1 persons lifetime can be looked at as "their" bankroll... Then it will gravitate towards EV no matter the table, day, casino, etc
I have never heard the Gambler's Fallacy expressed in terms of "the player is due" - only that "the table is due".
Like I said - unless you're counting cards, treat every bet as if it's your first one. Chances are, you won't enjoy it as much if you're too worried about chasing losses.
Quote: ThatDonGuy...Like I said - unless you're counting cards, treat every bet as if it's your first one. Chances are, you won't enjoy it as much if you're too worried about chasing losses.
I disagree with this. Counting cards or not, there's still a bankroll, house edge, EV, and a standard deviation based off the number of hands you've played. The only difference is counting cards (properly) will yield positive expectations. Even while non counters have negative expectations, that doesn't mean these expectations aren't measurable, or that they won't follow a 'pattern' of standard deviations along the line of EV. Thus, even for non-counters, if you're way below EV, you can expect in the long run to move towards your EV. It hasn't nothing to do with the gamblers fallacy.
Consider a coin toss, after 100 on average there will be 50 heads, but the SD = 5; so usually the range will be 40-60 (using 2SDs either side). After 10,000 tosses, the average is 5000, the usual range has grown to 4900-5100. Proportionally you expect to be much closer to the mean, but numerically it is greater.
Suppose you had a coin tossing game but were unlucky to be down $20. After 100 further tosses your range for those tosses would be 40W60L to 60W40L. Let's put in a .5% House Edge where you lose $1 but win 99c (for two bets H T you get back 1.99 for 2 bet = .5%).
Thus your total result for the 100 tosses would be -$20.40 to +$19.40 - so you have a quite small chance of recouping your initial losses.
Say you went on for 10000 tosses (4900W:5100L to 5100W:4900L) = -$788 to +$149. Strangely your chances of being ahead are slightly greater, but your expected loss would be greater.
After 1m tosses (499500-500500) (-$5999 to -$4005) it is almost impossible to be ahead.
In other words, if I'm playing perfect basic strategy at a -1% game, what's the probability that my actual losses will be at that 1% figure after playing 10 hands, 100,000 hands.. A million hands.
And is there a number of hands played where I'm 100% certain to be down 1% of the total of all bets risked?
Romes,
Really appreciate the time you took to write up your answer. This was exactly what I was trying to get at and thank you for the clear and detailed response. Iíll definitely have that saved up for future reference.
Quote: ThatDonGuyYou "could", but probability and statistics don't work that way.
First of all, there is no guarantee that you will "lose money in the long run"; that's just what is expected to happen.
Quote: beachbumbabsBut the cards have no memory, so without counting and betting accordingly, there's no reason to think you will "recover" from any trend, good or bad, and you shouldn't expect that you're due for winning or losing based on the math.
I've studied some basic statistics/probability and I understand that completely. I apologize if the question was phrased badly. The thought that I'd be due for a win or loss at a certain point in my game never crossed my mind. I understand I could either run below my EV forever, and never experience the "expected" upswing when my returns would converge back up to the EV, or be a forever winner and run above my EV for eternity.
Nevertheless, there is a probability attached to both of these ďextremeĒ outcomes, and it seems to me that, intuitively, the most probable (but not certain) distribution of my returns would be cyclical above and below the straight EV line (like Romes drew in his reply), given the balanced probabilities of a win/loss under certain rules and perfect basic strategy.
Quote: socksIf the process of playing a -EV game is enjoyable to you, don't over think things, just accept that you're going to lose $ in the long run, and set aside what you're willing to lose for the sake of entertainment.
Quote: ThatDonGuyLike I said - unless you're counting cards, treat every bet as if it's your first one. Chances are, you won't enjoy it as much if you're too worried about chasing losses.
I completely agree with both of your arguments and thanks for pointing it out. It shouldn't be anyone's intention to overthink gambling, or stress over the returns, but I just think itís in everyone's benefit to understand it better.
Quote: beachbumbabsYou made 2 ID's, and everyone is only allowed one. Possibly there was something in your sign-up that went wrong and you made the second ID, so instead of banning you I just killed the duplicate. Please don't make any more ID's; just use this one.
It was indeed an issue with the emails, but only intended to use this one so it's all right to kill the other.
charlieparick,
Thanks for the comment, but I couldít follow your math. My bad!
Quote: michael99000Is there a way to calculate the probability that my true losses will be equal to the EV of the game I'm playing after x number of hands?
In other words, if I'm playing perfect basic strategy at a -1% game, what's the probability that my actual losses will be at that 1% figure after playing 10 hands, 100,000 hands.. A million hands.
And is there a number of hands played where I'm 100% certain to be down 1% of the total of all bets risked?
I presume so. For example, the total probability that youíd be down 2 bets after 3 hands played would be the sum of the probabilities of each way that could arise (i.e. W-L-L, L-W-L, and L-L-W), since the events are mutually exclusive. Mathematically, I think itíd go like this:
P(2 bets down after 3 hands played) = P(WWL or LWL or LLW) = P(WWL) + P(LWL) + P(LLW) = 0.1251 + 0.1251 + 0.1251 = 0.3754
It assumes a house edge of 0.05%.
Again, cheers everyone for the discussion!
Quote: saliatHi,
I'm not as mathematically inclined, so I was wondering if you could comment on my thought process so far. If this has been answered before or is in the wrong place in the forum, I'd appreciate if you could forward me to the right place. Anyways, here it goes: assuming I'm not counting cards and only playing basic strategy, I understand that in the long-run I lose money as my EV is lower than my bet. However, it also means that my returns vary in the short-run, above and below the EV. Does that mean that I could exit on a positive variance and enjoy my winnings and, assuming I have sufficient bankroll, play through a negative variance until I converge back to the mean (or reach a positive variance again)? If this thought process is correct, is it an effective way to enjoy the game and is there a "standard" suggested bankroll?
Appreciate any comments!
Your EV is not related to your actual bet size.
No, this is not an effective way to enjoy the game. Of course you can exit the game after a run of positive variance, leaving with winnings. You can then play again, and quit when you are even, or when you have lost about how much you should have lost. That is similar to what almost everybody does.
The reason why I say it is not effective is because you are doing nothing different than anyone, except creating the illusion you have a system that is keeping you afloat. Which truly is doing nothing different than anyone. There is no standard bankroll for playing a -EV game. Over enough time, you will lose it all. Playing perfect basic strategy will slow the process of losing everything, as will a larger bankroll.
Bringing friends, drinking, and not caring about the lost cause of the gamble is an effective way to enjoy the game. Or if winning is your goal, card counting is an effective way. Certain betting systems dramtically improve your chances of winning a small amount of money by the end of the session, with only a tiny chance at a massive, life-altering loss...which may allow you to enjoy the game more.
If you're betting $10 a hand and your goal is, say, just winning $20 per table. You sit at one table, win $20. Next table you win $20. You keep doing this and you're up $100. Fantastic!
You go to the next table and after playing a few minutes, you're down $40. At this point, you need to win $60 (to be at a +$20) in order to be done with that table. All is good and well, except one problem:
You are more likely to lose $60 than you are to win $60.
Let's just say, for fun, you have a 49% chance of winning $60 and a 51% chance of losing $60 from that current point (so 49% you'll end at +$20 and 51% you'll be at -$100).
49% of the time you leave the table with +$20. Perfect!
But 51% of the time you lose that $60 and now are at -$100. Now you gotta win $120 to be at +$20. But now, it's more difficult to win that much, since you gotta play a lot more hands and will get ground down more.
So now, maybe you have a 47% chance of winning $120 and a 53% chance of losing $120.
47% of the time you win that $120, and you leave the table with +$20 overall.
The other 53% of the time, you'll end up at -$220. Dang, now you gotta win $240 back to get to the +$20 point! Now, you might have a 40% chance of winning $240 and a 60% chance of losing $240.
And so on.
My percentages were just numbers, I'm sure someone else can provide better %'s if they wanted to. But if we take my numbers to be true, then the following will be true:
Starting at the -$40 point....
49% of the time you win $60 to end the table at +$20.
49% * 47% of the time you lose $60 then win $120 to end the table at +$20.
49% * 47% * 40% of the time you lose $60 then lose $120 then win $240 to be at +$20.
51% * 53% * 60% of the time you end the table at -$440.
(0.49) + (0.51 * 0.47) + (0.51 * 0.53 * 0.40) ~ 83% : +20
(0.51 * 0.53 * 0.60) ~ 17% : -440
Eventually, you're going to get to the point where you have absolutely no hope. You are stuck so much money, you're never going to be able to get it back. And blackjack is not a good game to be playing if you're down a lot of money and trying to recoup. ie: Low variance.
If you're playing a game and are stuck a lot of money and are trying to recoup, you want a game with high variance. Hit a jackpot on a slot machine, or a royal flush on a video poker machine. Then again, chances of hitting a royal flush tend to be around 1 out of 40,000 hands.
You simply cannot beat the variance. PEOPLE WHO CAN GET AN ADVANTAGE OVER THE HOUSE CANNOT BEAT THE VARIANCE.
Quote: saliatSorry for the late reply. Really appreciate all the comments, very welcoming from everyone. Unfortunately, I donít have much blackjack knowledge yet to contribute back, but hopefully in the future!
Romes,
Really appreciate the time you took to write up your answer. This was exactly what I was trying to get at and thank you for the clear and detailed response. Iíll definitely have that saved up for future reference.
I've had a lot of references/information help me throughout my never ending journey, so I feel it's only right to pass some of it along. I'm glad you found the information useful!
Quote: michael99000Is there a way to calculate the probability that my true losses will be equal to the EV of the game I'm playing after x number of hands?
In other words, if I'm playing perfect basic strategy at a -1% game, what's the probability that my actual losses will be at that 1% figure after playing 10 hands, 100,000 hands.. A million hands.
And is there a number of hands played where I'm 100% certain to be down 1% of the total of all bets risked?
Yes, this can absolutely be calculated. You need to know your average bet. Then, to get your standard deviation for any 1 hand, 1.1*average bet. After that, for any number of 'events', or hands in our blackjack situation, to find your standard deviation just use the following: Sqrt(hands)*(1.1*avgBet). So what does this mean? I'll explain with an example:
- Assume -1% game... which if you're playing perfect basic strategy I'm not sure why this wouldn't be more like -.5%, but -1% is easier for the math so we'll go with it =P
- Assumes $100 average bet. Add/drop zeros if you want to say your AvgBet is something else, like $10...
| Number of Hands | Expected Value (EV) | Standard Deviation (STD) |
|---|---|---|
1 | -$1 | $110 |
100 | -$100 | $1,100 |
10,000 | -$10,000 | $11,000 |
*NOTE: Anything under at least 10k hands is just statistical noise. If you're way above, or below your standard deviation after 50 hands, 100 hands, 500 hands... that doesn't mean anything relevant. You can't yet tell if you're getting cheated, etc.
Explanations:
So if you have a -1% advantage, and you bet $100 on 1 hand... You'd expect in the long run to lose $1 in that situation. However, the standard deviation for that 1 hand is a little over $100, but that makes logical sense because if you bet 1 hand at $100, on average you're going to win or lose about $100.
Now if you bet $100 on 100 hands... at a -1% HE you're looking to lose, on average, a dollar a hand (in the long run). Thus, you can expect to lose $100, give or take your standard deviation... Sqrt(NumHands)*(1.1*AvgBet) = Sqrt(100)*(1.1*100) = 10*(110) = 1,100. Again this makes logical sense because if you were to bet $100 on 100 hands of blackjack (an hour or two of play), you might be up or down about $1,000.
The 10k hand example is the same thing extrapolated... Now you want to know what your probability of these situations are. For one standard deviation, it's about 66% accuracy. This means, you have a 2/3 chance of being within your standard deviation. In the chart above, for the 10k hands example... This means you have a 2/3 chance of being anywhere from $1,000 to -$21,000 after 10k hands. You have a 1/6 chance of being ABOVE $1,000, and a 1/6 chance of being below $21,000. To put them in more blunt numbers:
16.65% to be down more than -$21,000
66% to be between $1,000 and $-21,000
16.65% chance to be up more than $1,000
So to answer your question with this example... The probability you'd be at your EV (-$10,000) +- 1 standard deviation ($11,000), after 10,000 hands, is 66%. Rinse and repeat for any number of hands, with any average bet, etc.
...perhaps some of you can see how this would flip if you were playing with a 1% advantage =). You can see that even after 10k hands, you're 66% likely to be between -$1,000 and +$21,000, with only a 16.65% chance of being down more than $1,000. The power of counting becomes a bit more mathematically obvious at this point (you're removing luck the more hands you play).
Quote: RomesI've had a lot of references/information help me throughout my never ending journey.

Please try. Charlieparick hit the nail on the head. Your forward-looking expectation changes after each bet.Quote: saliatcharlieparick,
Thanks for the comment, but I couldít follow your math. My bad!
Quote: Sonuvabish
I caught your first broken link to photobucket, and your user account which I hope isn't your real name ;)
Quote: RomesQuote: Sonuvabish
I caught your first broken link to photobucket, and your user account which I hope isn't your real name ;)
Couldn't figure out how to post an image correctly. My user account? I think you are mistaken, I don't sign in to photobucket. There is something called user/almcelroy13 embedded in the photobucket links, which has nothing to do with me. Regardless, most of my internet sign-ons use fake names. I doubt photobucket somehow hacked my computer, put identifying info in the link, and I didn't notice.


