1-2-3-Out

PREFACE:
This is going to read like a math homework problem. It is in fact just a curiosity I stumbled across. Feel free to puzzle through some of the questions posed at the bottom of this post, or to comment on the methodology. Or not.

I was planning on using a new method to pick a random child from a class (size between 18 and 25), called 1-2-3-Out.

Kids line up in random order, and starting at the head of the line, I point to each child in turn, saying, "1, 2, 3, out." The "out" person sits down, and I continue. If I reach the end of the line, I start back over at the head of the line. Whichever child is left when the rest are called "out" is the Chosen One.

I got to thinking, "If I were a student, and I knew beforehand the method of picking was 1-2-3-out, where would I want to stand to maximize my chances of being chosen (assuming I had not solved it for my class size)? Where would I definitely NOT want to stand?"

I discovered some interesting facts, patterns, and non-patterns to the answers.

# of students	Winning pos.
2	1
3	2
4	2
5	1
6	5
7	2*
8	6
9	1
10	5
11	9
12	1
13	5
14	9
15	13
16	1
17	5
18	9
19	13
20	17
21	21

*Corrected

A pattern seems to emerge, where the winning position is "1", and the following winning positions continue by 4s. (5, 9, 13..)
There is an anomaly at class size 8, where "6" is the winner.
Doing these by hand, I noticed that as students were eliminated, there would be scattered individuals, plus a clump of 3, which would get whittled down to two, and one of those two would be the winner.

• Does anyone have a formula or explanation as to why this pattern occurs?
• Why does "6" jump out as a surprise winner in the midst of it all?
• Would there be any other surprise winners if the class size kept increasing?
• Is there any other significance to this counting method?
• What if this were played as "1-2-Out", or "1-2-3-4-Out"?

Edited to correct the Student = 7, Winner = 2 result.

-Dween!

I vote you roll a die to chose the out number. You could roll the first time and who ever was "out" could roll the next.

Isn't this modular arithmetic?

I wrote a script to find who wins in 1-2-3-out.

1) with 7 people, #2 actually wins, not #1.
2) Your pattern of starting with 1 breaks down at the next class size, but the 4 increase pattern stays. This actually helps explain the 7,8 result:

22 3
23 7
24 11
25 15
26 19
27 23
28 27
29 2
30 6
31 10
32 14
33 18
34 22
35 26
36 30
37 34
38 38
39 3
40 7
41 11
42 15
43 19
44 23
45 27
46 31
47 35
48 39
49 43
50 47

Quote: dwheatley

I wrote a script to find who wins in 1-2-3-out.

1) with 7 people, #2 actually wins, not #1.
2) Your pattern of starting with 1 breaks down at the next class size, but the 4 increase pattern stays. This actually helps explain the 7,8 result:

22 3
23 7
24 11
25 15
26 19
27 23
28 27
29 2
30 6
31 10
32 14
33 18
34 22
35 26
36 30
37 34
38 38
39 3
40 7
41 11
42 15
43 19
44 23
45 27
46 31
47 35
48 39
49 43
50 47

Yup. In Excel, if you enter in the number of students in column A (starting with '1' in A1), and column B is the winner, manually enter '1' at cell B1, and enter this formula into B2 and c/p down column B: =IF(MOD(B1+4,A2)=0, A2, MOD(B1+4,A2))

The winner is constantly incremented by 4, but the modulus (or wrap-around point) is constantly increased by 1, so these sub-patterns that you notice have different initialized values.

First, a *facepalm* for messing up the Class Size 7 result.

Second, I can't believe I stopped at 21... if I had gone a step further, I would've noticed a new pattern.

Third, jc2286, how did you come up with that formula?

Fourth, the modulus/wrap around points do not necessarily increase by 1 each time... but not sure if they have any rhyme or reason other than the formula given.

Quote: Dween

First, a *facepalm* for messing up the Class Size 7 result.

Second, I can't believe I stopped at 21... if I had gone a step further, I would've noticed a new pattern.

Third, jc2286, how did you come up with that formula?

Fourth, the modulus/wrap around points do not necessarily increase by 1 each time... but not sure if they have any rhyme or reason other than the formula given.

I was playing around in Excel trying to find the pattern, and it didn't take me long once I realized the Class 7 result was wrong (I did around the same time as dwheatley but he posted it first).

The modulus does increase by 1 each time. It's equal to the Class Size. Look at the pattern (always adding 4 to the prior result) before applying the modulus for the current class size:

1 1 -> 1 mod 1 = 1
2 (1+4) -> 5 mod 2 = 1
3 (1+4) -> 5 mod 3 = 2
4 (2+4) -> 6 mod 4 = 2
5 (2+4) -> 6 mod 5 = 1
6 (1+4) -> 5 mod 6 = 5
7 (5+4) -> 9 mod 7 = 2
8 (2+4) -> 6 mod 8 = 6
9 (6+4) -> 10 mod 9 = 1

And the reason the formula needs that IF statement instead of just =MOD(B1+4,A2) is because when the mod=0 it actually = the last person (much the same way with a clock, which is mod12, but 0 o'clock is 12 o'clock).

I am probably overcomplicating this, but here goes...

The following graph shows the position of the winner (red) for each number of students (blue) from 2 to 1000:



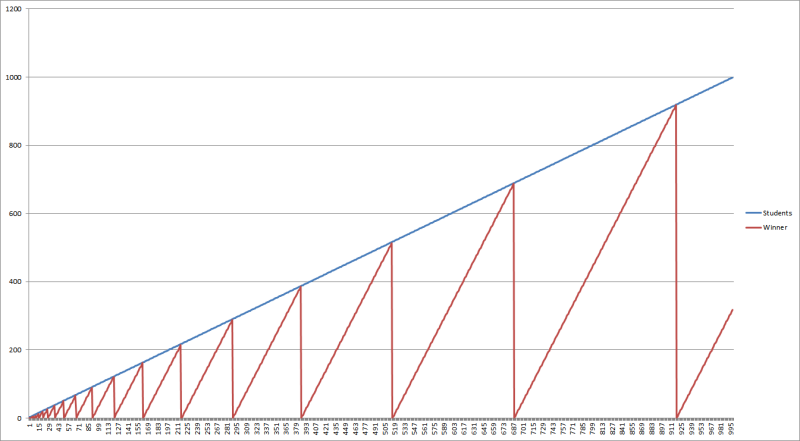
Integer sequence A072493 seems to be related. When the number of students equals one of the numbers in that sequence, the position of the winning student resets to 0, 1, or 2; I would call this the offset. The offset appears to be the remainder when something is divided by 3. Each subsequent winning student number is then incremented by 4 until the next number in the sequence. Therefore, the formula to compute the position of the winning student based on the number of students will probably look like this:





The  something  is a mystery; it's not the number of students or anything I can think of at the moment.

The  nearest_sequence_number  is the nearest sequence number which is less than or equal to the  number_of_students .

The  + 1  at the end of the formula is to convert student #0 to student #1, for example.

I vaguely recall a similar problem where a crazed Roman general decimates his legion again and again, until only one is left. In this case you start out with a hundred Roman soldiers and kill every thenth one (like they're going to sit still for that...)

Anyway, I supose there's a general solution.

That definitely seems overcomplicated, especially compared to my solution.

However, it dawns on me that both of our solutions require knowing winners from smaller class sizes. The trick will be to come up with a one-hot solution as soon as it's known how big the class is. Example: sum(1 to n) requires adding an incremented integer to the previous sum n times... or, just use the one-hot solution n(n+1)/2. We need to find that equation for this problem.

Quote: jc2286

However, it dawns on me that both of our solutions require knowing winners from smaller class sizes.

No, only yours does. My formula uses a mystery dividend and a variable that I'm not sure how you would go about calculating. :)

Quote: jc2286

The trick will be to come up with a one-hot solution as soon as it's known how big the class is. Example: sum(1 to n) requires adding an incremented integer to the previous sum n times... or, just use the one-hot solution n(n+1)/2. We need to find that equation for this problem.

That was my goal when I started looking at the data, but I didn't get very far.

Quote: jc2286

Yup. In Excel, if you enter in the number of students in column A (starting with '1' in A1), and column B is the winner, manually enter '1' at cell B1, and enter this formula into B2 and c/p down column B: =IF(MOD(B1+4,A2)=0, A2, MOD(B1+4,A2))

You can achieve the same result by either:

Numbering the students from 0 to n-1, where n=the number of students there are; and then using the formula =MOD(B1+4,A2)

or, to keep the numbering from 1 to n, use the formula: =MOD(B1+3,A2)+1

Personally, I like numbering the students from 0 to n-1, as this is how things are typically done when programming.

Quote: JB

or, to keep the numbering from 1 to n, use the formula: =MOD(B1+3,A2)+1

I like that, nice. Much cleaner.

I prefer starting at 0 as well since I'm a programmer. But I think it'll be several decades if not centuries before the layman thinks that way, if ever.

Quote: jc2286

I like that, nice. Much cleaner.

I prefer starting at 0 as well since I'm a programmer. But I think it'll be several decades if not centuries before the layman thinks that way, if ever.

We must make them see our side. I can't stand the thought of wasting array[0], or subtracting 1 every time you access array[].