A special fraction that is as close to Pi as possible

The fraction 937246158 / 298341567 is a close approximation to the value of Pi. 937246158 / 298341567 = 3.14152053

What is interesting about both the numerator and the denominator is that each of these nine-digit numbers both consist of all of the digits 1 through 9, with no repeats.

The fraction 573819264 / 182653479 also contains these properties and is even closer to Pi, albeit very slightly, than the first fraction. 573819264 / 182653479 = 3.14157314

Question: What nine-digit numerator and nine-digit denominator, each containing the digits 1-9, is CLOSEST to the value of Pi?

------------------------------------------------------------------

P.S. While looking for something else, I came across this question and I thought it was very interesting. I had never heard the question before, so hopefully one or two others here have not heard it either.

The website I visited did not know or provide the answer, so I spent a few hours earlier this morning computing it on my own. I had a lot of fun in doing so.

However, as I should have expected, after arriving at my answer I soon realized many other websites also contained this question and many of them often posted the correct answer...meaning I had not discovered anything new. Arrgh! Darn!

That's one of the big disadvantages with math. When you learn a new concept, or discover something interesting, you soon realize you did not learn anything that hasn't been known long before. In fact, there's a good chance people like Euler and Pascal probably knew it when they were still in their diapers.

Since the answer to the above question is so readily available, here's a bonus question that might not be so easy to find: What is the SECOND closest nine-digit numerator / nine-digit denominator that comes as close to Pi as possible?

some other interesting fact, the smallest fraction with an impressing 6 decimal accuracy:

355/113 = 3.14159292035...

Quote: EdCollins

Since the answer to the above question is so readily available, here's a bonus question that might not be so easy to find: What is the SECOND closest nine-digit numerator / nine-digit denominator that comes as close to Pi as possible?

Here are the first 20 :)

467895213/148935672=3.1415926535048
429751836/136794258=3.14159265369165
813569274/258967143=3.14159265370588
928146375/295438167=3.14159265346376
546213789/173865249=3.14159265374531
937186245/298315647=3.14159265336826
621583974/197856324=3.14159265386938
896452713/285349761=3.1415926540762
613987452/195438276=3.14159265301747
784321596/249657318=3.14159265301408
529436817/168524973=3.14159265285864
481573629/153289647=3.14159265432975
842935167/268314597=3.14159265438697
529136487/168429375=3.14159265270681
549231876/174825936=3.14159265247692
683719254/217634598=3.14159265246971
915628734/291453678=3.14159265473397
613825497/195386724=3.1415926549851
621574983/197853462=3.14159265507318
579234168/184375962=3.14159265512063

22/7 is close enough in my book

Quote: andysif

some other interesting fact, the smallest fraction with an impressing 6 decimal accuracy:

355/113 = 3.14159292035...

That uses 6 total digits in the fraction and approximates pi to 3.1415929. The real pi is 3.1415926. So it uses 6 digits to come up with 7 correct digits.

22/7 uses 3 and is right to 3.

Can anyone get improve upon 355/113, where the degree of success is the number of total digits saved, in this case 1 (using 6 to get pi right to 7 digits).

Ref: pi=3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679

I'm not going to risk severe brain trauma by attempting to come up with better fractions. I just thought I would mention that the very first time that I saw the 355/113 approximation for Pi was in the instruction manual for an HP35 calculator I purchased in 1973. As an exercise in learning to use the RPN calculation technique, they suggested calculating the percentage error of this ratio as an approximation to Pi. The manual noted that an easy way to remember this particular fraction is to write the first three odd numbers twice each, then separate them in the middle with a long division symbol like:


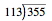
Off-topic but related to my own post: I think the HP35 was the first commonly-available portable electronic calculator that could perform calculations with transcendental functions like logarithms, trig functions, etc. It provided a lot more significant digits than a slide rule. I bought mine after they came out with the HP45 and the price on the HP35 dropped from $400 to $300. About a year later, TI came out with their comparable calculators for around $150. Within a couple more years, slide rules were novelty "antiques". I still have one or two in my desk drawer.

This is getting off topic, but my father gave me an HP15C as a high school graduation present, and I've been using daily, almost hourly, ever since. How far HP has fallen, in my opinion, to the computer that caught fire on me a few years ago.

Quote: andysif

some other interesting fact, the smallest fraction with an impressing 6 decimal accuracy:

355/113 = 3.14159292035...

Archimedes concluded that PI was smaller than 3+1/7 and bigger than 3+10/71.
As 3+1/7 = 3+16/112 at first glance it seems fairly unremarkable that 3+16/113 =355/113 is a better approximation. But that improvement took humanity almost 800 years to make (and the western world over 1800 years to accomplish).

It is not clear to me if the Chinese in the 5th century knew that 355/113 was also an upper bound.

If you go back and read about how these calculations were done, even getting pi = 22/7 was a remarkable accomplishment.

I do think that Archimedes may have been one of the greatest minds of all of history. I am big fan of his. His murder was an unbelievable tragedy.

All I knowl about pi is the mnemonic device for the first nine places...may I have a large container of orange juice

Quote: Wizard

This is getting off topic, but my father gave me an HP15C as a high school graduation present, and I've been using daily, almost hourly, ever since. How far HP has fallen, in my opinion, to the computer that caught fire on me a few years ago.

Ah... HP calculators. I remember saving $200 so I could buy a used HP48SX in high school. It was worth every penny and put my TI83 to shame, which I gave to my sister. HP calculators were awesome.

Quote: Wizard

Can anyone get improve upon 355/113, where the degree of success is the number of total digits saved, in this case 1 (using 6 to get pi right to 7 digits).

Well, I can't. I tried.

A few close calls that match the degree of success of 1:

21 digits in fraction, 22 accuracy
21053343141 / 6701487259 = 3.1415926535897932384623

37 digits in fraction, 38 accuracy:
2646693125139304345 / 842468587426513207 = 3.14159265358979323846264338327950288418

deleted

I don't know if this has been mentioned elsewhere in this thread, but this discussion falls under the topic of "continued fractions." So very long ago now, I used to teach this material at Ohio University. I designed an entire introductory number theory course around the book "Continued Fractions" by C.D. Olds.

At any rate, the key theorem that guarantees and endless supply of these interesting fractions is Hurwitz's Theorem.

Very roughly speaking, for any irrational number, there are infinitely many fractions that give accuracy of approximation that is double the number of digits (or better) in the denominator of the fraction. So 355/113 gives 6 places (113 has 3 decimals). The fraction given by EdCollins above has 18 digits in the denominator and 38 digits in accuracy.

When I taught intro to programming at UCSB, this was one of my standard first projects:

=========================
Programming Assignment 3 (25 points)
Engr 3, Fall 2000
Due: Wednesday, October 25, 2000, 11:59 PM.

Instructions: Complete the following parts.

Part A (10 points) The number 153 is very interesting. In fact, 153 = 1*1*1 + 5*5*5 + 3*3*3, that is, 153 is the sum of the cube of its digits: 153 = 1^3 + 5^3 + 3^3. Your task in this programming project is to write a program that determines all integers between 100 and 999 that are the sum of the cubes of their digits. That is, find all numbers xyz such that xyz = x^3 + y^3 + z^3. The name of this program must be “Gath.c” . (Question: why Gath?) The grader will run your program to verify that your program outputs the correct numbers in a reasonably brief period of time.


Part B (15 points) The value of pi to 15 decimal places is PI = 3.141592653589793 . . . Your job is to write a program that can be used to find decent approximations to PI. More specifically, your program must find integers N and D such that the fraction N/D is the best possible approximation to PI and such that D < 1,000,000.

For example, 3/1 = 3.0 is fairly lame, 22/7 = 3.1428 is pretty good, but 355/113 = 3.14159292 is even better. A really bad try is 3141592/1000000 = 3.141592, which isn’t even as good as 355/113. So, what’s the best you can do? Remember, you can use any denominator at all, but it must be less than 1,000,000.

You will need to use the absolute value function fabs and include math.h (see page 767). Also, to get your program to print out a double to 15 decimal places you will need to use the qualifier %1.15f instead of just %f in the printf statement where you print out your results.

The name of this program must be “findPi.c” A working sample program is available in ~teliot/ENG3/pa3. However, this program only solves the problem for a maximum denominator of 100,000. Note that the program prints increasingly accurate approximations. You must consider questions of efficiency for this program, a program that does not quickly print out the correct answer will not receive full credit.

Quote: teliot

Also, to get your program to print out a double to 15 decimal places you will need to use the qualifier %1.15f instead of just %f in the printf statement where you print out your results.

Not that it matters much, but this is wrong. The qualifier should be %17.15f.
The number before radix is the total width of the output.

Quote: weaselman

Not that it matters much, but this is wrong. The qualifier should be %17.15f.
The number before radix is the total width of the output.

I'm not sure what I don't know here, not that it matters.

Quote: teliot

Your task in this programming project is to write a program that determines all integers between 100 and 999 that are the sum of the cubes of their digits. That is, find all numbers xyz such that xyz = x^3 + y^3 + z^3.

I expected more than this, but I come up with just four. 153, 370, 371, and 407.

Your class sounds like it was a lot of fun.

Well 1.15 happens to appear to work in this case, because the width qualifier (1) is invalid (the output can't be fit into one character), so it gets ignored. You may also want to try ".15f" and "20.15f" to see how it works.

Quote: EdCollins

I expected more than this, but I come up with just four. 153, 370, 371, and 407.

Your class sounds like it was a lot of fun.

See this for more information about the number 153. It's really quite an amazing number. If you look it up on Google, you will find a lot more, especially its use and possible meaning in the Bible.

Quote: EdCollins

I expected more than this, but I come up with just four. 153, 370, 371, and 407.

Your class sounds like it was a lot of fun.

Here is a problem that I really enjoyed giving my first quarter Freshmen. Try writing this and having your program print out the fractions with MAX = 1000.

Part D (10 points) The name of this program is “fractions.c”. In it you will ask the user for a single integer, called MAX. Your program will proceed to print out all the fractions between 0 and 1, in lowest terms, with a denominator between 1 and MAX (inclusive), in increasing order. For example, if you input a value of
MAX = 5, then your program will print out:

0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1

In the book "A Passion for Mathematics", Clifford A. Pickover published a number of formulas and fractions that approximate or calculate Pi.

Quite a few of the approximations and formulas come from mathematician Srinivasa Ramanujan.

This one converges so slowly, it takes 300 terms before it is accurate to 2 decimal places:
Pi = 4(1-¹/₃+¹/₅-¹/₇+¹/₉...)

This one only uses the number 2 to calculate Pi:
Pi = 2 x (²/_√2) x (²/_√(2+√2)) x (²/_{√(2+√(2+√2))})...

A formula for Pi that has Pi in it:
Pi = (1+¹/_Pi)^1+Pi

With continued fractions:
⁴/_Pi = 1+¹/_{(3+⁴/(5+⁹/(7+¹⁶/(9+...}

And more:
⁴/_Pi = ¹/_{(1+^1²/(2+^3²/(2+^5²/(2+7²...}

Pi = √(6 x (1+¹/₄+¹/₉+¹/₁₆+¹/₂₅...))

^Pi/₂ = 1 + ¹/₃(1+²/₅(1+³/₇(1+⁴/₉(1+...))))

An approximation:
Pi ≈ (²¹⁴³/₂₂)^1/₄

Correct to 8 places:
Pi ≈ ^99²/_2206√2

use Bellards formula

Wins my vote for oldest revived thread

My favorite is apple pie.

Quote: MaxPen

My favorite is apple pie.

Mmmmm. Deep dish. Only 2 better. Mom's lemon meringue, and mom's pecan pie. Seriously. There is no bakery that can out-pie her.

My only contribution to this thread. I don't understand the origin of these bizarre fractions. I thought 22/7 was the be-all and end-all. Silly wabbit .