Is the House Edge context-dependent?
July 22nd, 2025 at 8:32:45 AM
permalink
I described the "Magic Trick At The 000 Roulette Table", where a magician makes 5.39 percentage-points of house edge disappear for a player at the triple-zero roulette table by playing himself (the magician) at 7.69% house edge, which magically never affects his own bankroll. Using this phenomenon, the magician is able to reduce the house edge (or player's disadvantage) for the player to a mere 2.30%.
To show that this actually works, I set up a simulation over 3900 rolls.
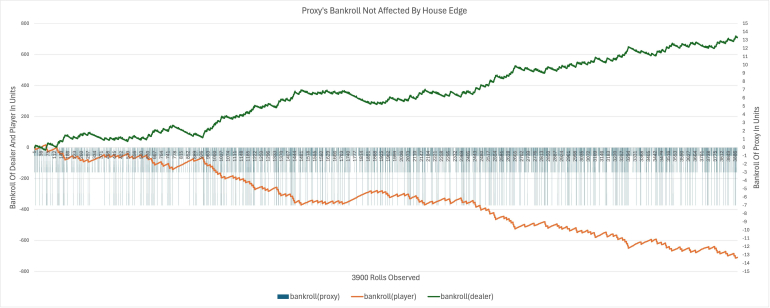
The chart of the bankrolls shows that the amount lost by the player is completely collected by the dealer, while the magician's (the proxy's) bankroll falls back to zero with each of the player's resolved bets. None of the money is withdrawn by the magician (the proxy) at any time.
However:
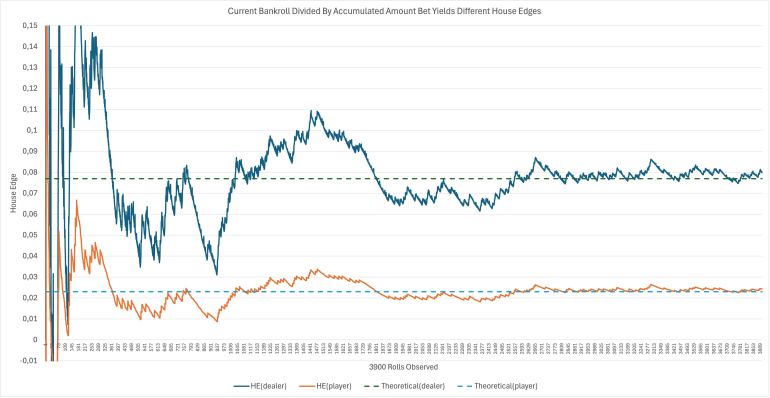
The dealer, as the representative of the casino, observes a house edge of 7.69% relative to the amount bet.
The player only experiences 2.30% relative to his 15-units-wager in the "private" bet with the magician (the proxy).
Had the dealer offered the 15-units-bet to the player directly, the casino would have assigned a 2.30% (not 7.69%) house edge to this side bet.
In your opinion: Is the house edge dependent on context?
To show that this actually works, I set up a simulation over 3900 rolls.
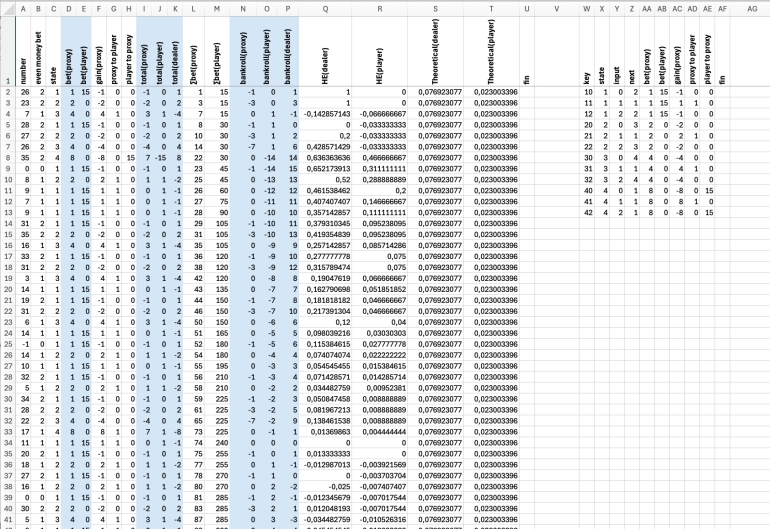
Top of the simulation.
...
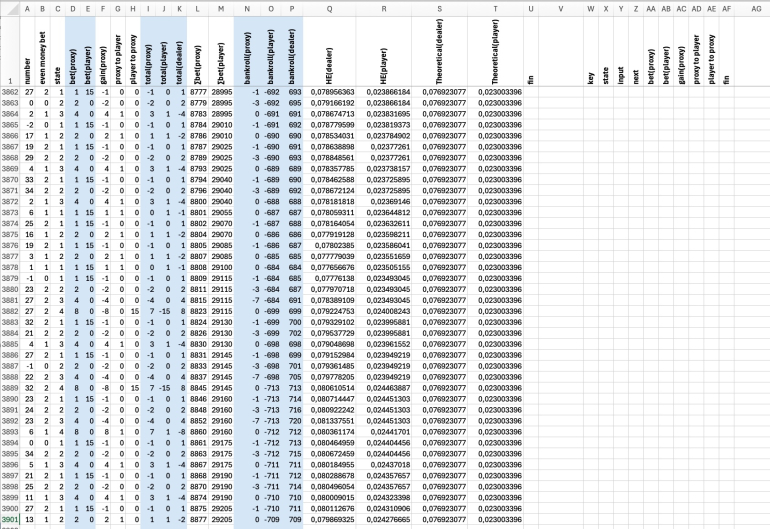
Bottom of the simulation.
...
Bottom of the simulation.
The chart of the bankrolls shows that the amount lost by the player is completely collected by the dealer, while the magician's (the proxy's) bankroll falls back to zero with each of the player's resolved bets. None of the money is withdrawn by the magician (the proxy) at any time.
However:
The dealer, as the representative of the casino, observes a house edge of 7.69% relative to the amount bet.
The player only experiences 2.30% relative to his 15-units-wager in the "private" bet with the magician (the proxy).
Had the dealer offered the 15-units-bet to the player directly, the casino would have assigned a 2.30% (not 7.69%) house edge to this side bet.
In your opinion: Is the house edge dependent on context?
Imho this example shows that "amount bet" and "wager" in general are fundamentally different, although this is neither visible nor relevant during flat betting, because in that case both amounts are identical.
The difference becomes significant with varying bet amounts.
Now the "amount bet" is no longer the primary source of profit for the casino, because losses, the player suffers on smaller bets, are compensated by winnings, the player earns on larger bets. As long as the player is compensated, he doesn't lose any money but rather wins the remaining amounts and therefore does not contribute to any of the casino's profit.
Only in the losing case of the (finite) sequence, the player actually loses his money, which now can be called the "wager" and which will be the actual source of casino profit (player loss - player win > 0).
In the given example the fifteen units are the wager, lost in the losing case, i.e. after losing four rolls in a row.
Conclusion
"Expected value divided by the wager" could be a uniform definition of the "house edge" which would allow comparing games unambiguously.
The difference becomes significant with varying bet amounts.
Now the "amount bet" is no longer the primary source of profit for the casino, because losses, the player suffers on smaller bets, are compensated by winnings, the player earns on larger bets. As long as the player is compensated, he doesn't lose any money but rather wins the remaining amounts and therefore does not contribute to any of the casino's profit.
Only in the losing case of the (finite) sequence, the player actually loses his money, which now can be called the "wager" and which will be the actual source of casino profit (player loss - player win > 0).
In the given example the fifteen units are the wager, lost in the losing case, i.e. after losing four rolls in a row.
Conclusion
"Expected value divided by the wager" could be a uniform definition of the "house edge" which would allow comparing games unambiguously.
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
