I'm hoping to get some help calculating the progressive jackpot for a three card poker straight flush (paying 10% of the jackpot) and the mini royal (paying 100% of the jackpot). I can do it for the mini royal, that's pretty straightforward but how do I incorporate the additional SF?
And in particular it would be good to do in Excel so i can modify the contribution amount and the reset amount and see how it impacts the house edge.
So far I have: (1-contribution rate-((P(SF)*0.1)+(P(MR)*1))), which, if the contribution amount is $5 = -0.00038 but i can only modify the contribution rate in that formula in Excel and its no good to me. I'd like a formula or Excel setup that lets me modify the contribution amount (in dollars) and the seed amount (in dollars) and for that to show me the house edge dynamically.
Appreciate any help or direction, thank you!
Start with the number of unique 3-card combinations in a 52 card deck. 52 x 51 x 50 which is 132600. You'll need that number later.
Now we do the royals. AKQ, AQK, KAQ, KQA, QAK, QKA are all 3-card royals. So that's 6 per suit and you have 4 suits, so 24 out of 132600 are royals and that coefficient is 0.000180995
Next step is the straight flushes. What are those? A23, 234, 345, 456, 567, 678, 789, 89T, 9TJ, TJQ. So that's 10, and as we saw with the royals each one has 6 possible ways to do it. 10, times 6, times 4 suits, for 240 out of 132600. What a coincidence! That coefficient is 0.00180995
So being the SF is 10% of the royal, they will both have an equal contribution. It's the jackpot amount X 0.000180995 X 2.
What you're doing that involves the contribution amount I'm not sure what you mean.
Quote: AutomaticMonkeyYou're working too hard! All you need is two coefficients.
Start with the number of unique 3-card combinations in a 52 card deck. 52 x 51 x 50 which is 132600. You'll need that number later.
Now we do the royals. AKQ, AQK, KAQ, KQA, QAK, QKA are all 3-card royals. So that's 6 per suit and you have 4 suits, so 24 out of 132600 are royals and that coefficient is 0.000180995
Next step is the straight flushes. What are those? A23, 234, 345, 456, 567, 678, 789, 89T, 9TJ, TJQ. So that's 10, and as we saw with the royals each one has 6 possible ways to do it. 10, times 6, times 4 suits, for 240 out of 132600. What a coincidence! That coefficient is 0.00180995
So being the SF is 10% of the royal, they will both have an equal contribution. It's the jackpot amount X 0.000180995 X 2.
What you're doing that involves the contribution amount I'm not sure what you mean.
link to original post
JQK is also a SF. May I ask why youíre counting every permutation? Does the order matter in this situation?
Quote: camaplQuote: AutomaticMonkeyYou're working too hard! All you need is two coefficients.
Start with the number of unique 3-card combinations in a 52 card deck. 52 x 51 x 50 which is 132600. You'll need that number later.
Now we do the royals. AKQ, AQK, KAQ, KQA, QAK, QKA are all 3-card royals. So that's 6 per suit and you have 4 suits, so 24 out of 132600 are royals and that coefficient is 0.000180995
Next step is the straight flushes. What are those? A23, 234, 345, 456, 567, 678, 789, 89T, 9TJ, TJQ. So that's 10, and as we saw with the royals each one has 6 possible ways to do it. 10, times 6, times 4 suits, for 240 out of 132600. What a coincidence! That coefficient is 0.00180995
So being the SF is 10% of the royal, they will both have an equal contribution. It's the jackpot amount X 0.000180995 X 2.
What you're doing that involves the contribution amount I'm not sure what you mean.
link to original post
JQK is also a SF. May I ask why youíre counting every permutation? Does the order matter in this situation?
link to original post
Ah yes, thanks, felt like I was doing something wrong! So the right number is (0.000180995 x jackpot) + (0.000199095 x jackpot). The second term is 264 permutations / 132600 possibilities, times 10% of the jackpot.
I did it this way to illustrate that if you're looking for +EV jackpots on a single deck game all you need is a coefficient for each win. The Wizard has probably already defined all these numbers in the game analysis part of WoO.
Quote: AutomaticMonkeyYou're working too hard! All you need is two coefficients.
Start with the number of unique 3-card combinations in a 52 card deck. 52 x 51 x 50 which is 132600. You'll need that number later.
What you're doing that involves the contribution amount I'm not sure what you mean.
Thank you for your reply! I'm a bit confused about the 132,600, I thought there were 22,100 ways to get a 3-card hand (52c3)?
What I'm after (the reason I'm using the contribution amount - the amount that's taken from the cost to play the jackpot and added to the progressive jackpot amount each time it's bet) is a table like this, where i can change the modifiable cells to see how they impact the RTP. The bit I don't get is how to input the probability of winning given there are two winning outcomes, each with different returns (10 and 100%).
Probability of winning: (MR and SF?)%
Odds of winning (1-in): (=1-above)
Cost to play: $5.00
Contribution amount: modifiable ($)
Jackpot seed value: modifiable ($)
Seed payout return: x%
+ Contribution %: y%
= Return to player: x+y%
Quote: joanmillerQuote: AutomaticMonkeyYou're working too hard! All you need is two coefficients.
Start with the number of unique 3-card combinations in a 52 card deck. 52 x 51 x 50 which is 132600. You'll need that number later.
What you're doing that involves the contribution amount I'm not sure what you mean.
Thank you for your reply! I'm a bit confused about the 132,600, I thought there were 22,100 ways to get a 3-card hand (52c3)?
Almost the same thing- there are 22100 different 3-card hands you can get. (assuming a standard 52-card deck.) But there are 6 different ways to get each 3-card hand. And 22100 x 6 is 132000. That's a more "mathematically pure" way to express it because you would do it that way if you had multiple decks. Or if cards were removed from the deck.
Quote: joanmiller
What I'm after (the reason I'm using the contribution amount - the amount that's taken from the cost to play the jackpot and added to the progressive jackpot amount each time it's bet) is a table like this, where i can change the modifiable cells to see how they impact the RTP. The bit I don't get is how to input the probability of winning given there are two winning outcomes, each with different returns (10 and 100%).
Probability of winning: (MR and SF?)%
Odds of winning (1-in): (=1-above)
Cost to play: $5.00
Contribution amount: modifiable ($)
Jackpot seed value: modifiable ($)
Seed payout return: x%
+ Contribution %: y%
= Return to player: x+y%
link to original post
Good news- they don't affect the RTP. The jackpot is what it is when you are dealt your hand, and that number alone is what you would use to calculate the EV of that bet for that hand. Being these tables are linked anyone who bets it will be contributing to the jackpot for the next hand, but that's next hand and it has nothing to do with the one you're playing right now. And whether you or somebody at another table makes that contribution makes no difference.
I think I havent been clear, in what im trying to do. My goal is to see how changing the seed value and the contribution amount (added to the progressive jackpot amount, taken from the bet on the jackpot, leaving a portion to go to the house directly) change the house edge of the jackpot bet.
So if there are 22,100 ways of dealing 3 cards from a single deck and the player wins if they get one of 48 hands (4 mini royals and 44 straight flushes), how do we factor in the percentage difference of the payouts 10% vs 100%, and then use that to calculate the house edge of the jackpot bet. I take it you are saying that the P(win) = MR+SF, which i get but since the payouts arent the same im stuck with how to calc the house edge from here, perhaps my table above is also not the right format to do this?
Quote: joanmillerThank you for the reply.
I think I havent been clear, in what im trying to do. My goal is to see how changing the seed value and the contribution amount (added to the progressive jackpot amount, taken from the bet on the jackpot, leaving a portion to go to the house directly) change the house edge of the jackpot bet.
So if there are 22,100 ways of dealing 3 cards from a single deck and the player wins if they get one of 48 hands (4 mini royals and 44 straight flushes), how do we factor in the percentage difference of the payouts 10% vs 100%, and then use that to calculate the house edge of the jackpot bet. I take it you are saying that the P(win) = MR+SF, which i get but since the payouts arent the same im stuck with how to calc the house edge from here, perhaps my table above is also not the right format to do this?
link to original post
And this is the answer: it doesn't change it. At all. Ever. Not even a little bit. The value of the jackpot and the probability of winning each prize are exactly what they are when placing your bet, and what happened on the last hand, or will happen on the next hand, or what the casino does with whatever money that was bet are not part of the equation.
Quote: acesideBut the OP is asking, what percentage of a playerís $5 bet on the jackpot should go to the house as a profit for operating the jackpot? While the remaining part will all go to the jackpot.
link to original post
yes this is what im asking as well as what should the seed amount for the jackpot be in order to achieve an x% house edge on the progressive jackpot bet. im asking because the seed amount and the contribution amount (taken from the player's bet and added to the progressive) are necessary to calculate the house edge. I understand that the probabilities of winning dont change and i appreciate the other replies
100% x 1/12 + 10% x 11/12 = 17.5%.
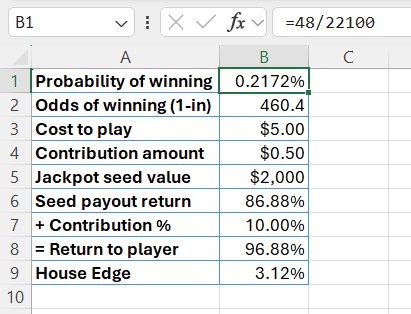
I'm so sorry but can you help me understand how to incorporate that 17.5% into this table, which I have a feeling is totally wrong, but might help to show what I'm trying to get?
1000 x 17.5% x (24+264)/132600 =0.38 =38%.
Therefore, when the jackpot meter is greater than $2631, a player may gain an expected return of greater than 100%, so players should always play it now.
However, this jackpot sounds too good to exist. Here is a Mini Royal jackpot from Wizard:
Three Card Poker Progressive ó Version 1
HAND: PAYS
Mini Royal in spades: Jackpot
Mini Royal: $500
Straight Flush: $100
Three of a Kind: $90
The expected return on non-jackpot payout is 47.87% and that on jackpot is 4.52% for each $1000 in the jackpot. These numbers sound more reasonable.
Iím not good at Excel. If you are ok with using the Wizardís version of pay table as an example, Iíd like to consider it more into it. It has to be realistic for any time and effort. Iíd like to invite DogHand to do an Excel table for you.


