37th outcome using two dice
January 29th, 2024 at 12:23:11 PM
permalink
I am setting up an experiment using two dice, and I need to account for a 37th outcome which has a 1/36 chance of occurring. For the standard 36 outcomes I am using two dice of different color to differentiate which number occurs on which die. But, how can I capture a 37th outcome? Maybe if the same die values occur on the next roll?
January 29th, 2024 at 12:26:24 PM
permalink
Are there supposed to be 36 possible outcomes, or 37?
Are they all supposed to have equal chances?
Are they all supposed to have equal chances?
May the cards fall in your favor.
January 29th, 2024 at 12:30:09 PM
permalink
37 outcomes
equal chances
equal chances
January 29th, 2024 at 12:34:52 PM
permalink
Are the odds 1/36 if I have a blue die that rolls a 3 and a yellow die that rolls a 2, then the same outcome occurs on the next roll?
January 29th, 2024 at 12:54:05 PM
permalink
Quote: TxGammonI am setting up an experiment using two dice, and I need to account for a 37th outcome which has a 1/36 chance of occurring. For the standard 36 outcomes I am using two dice of different color to differentiate which number occurs on which die. But, how can I capture a 37th outcome? Maybe if the same die values occur on the next roll?
link to original post
Your probability sum would add up to more than 100% then. You are looking for overlapping events? Where a role of the die can signify more than one outcome?
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
January 29th, 2024 at 1:08:08 PM
permalink
Are the odds 1/36 if I have a blue die that rolls a 3 and a yellow die that rolls a 2, then the same outcome occurs on the next roll?
January 29th, 2024 at 1:10:38 PM
permalink
I am trying to capture values of 0 thru 36 using a pair of dice.
January 29th, 2024 at 1:19:04 PM
permalink
A roll of 3 on the blue die with 2 on yellow corresponds to a value of 9.
Another roll of 3 on the blue die with 2 on yellow corresponds to a value of 9 as well, but if the odds of that event (same dice roll back to back, nothing special about the 3 and the 2) occurring is 1/36 a value of 0 would be recorded as well.
9
9
0
Another roll of 3 on the blue die with 2 on yellow corresponds to a value of 9 as well, but if the odds of that event (same dice roll back to back, nothing special about the 3 and the 2) occurring is 1/36 a value of 0 would be recorded as well.
9
9
0
January 29th, 2024 at 1:19:30 PM
permalink
Quote: TxGammonI am trying to capture values of 0 thru 36 using a pair of dice.
link to original post
Tell us why…. But I think you will fail. 1 through 36 is what you can do.
January 29th, 2024 at 1:22:23 PM
permalink
Quote: SOOPOOQuote: TxGammonI am trying to capture values of 0 thru 36 using a pair of dice.
link to original post
Tell us why…. But I think you will fail. 1 through 36 is what you can do.
link to original post
really, not useful.
January 29th, 2024 at 1:41:29 PM
permalink
If you roll any pair, treat it normally in terms of what it signifies but on the next roll:
- if you roll any pair it signifies a new roll with 37 (or 0) as an outcome
- otherwise, this next roll is void with no outcome, reset and go onto another roll.
- if you roll any pair it signifies a new roll with 37 (or 0) as an outcome
- otherwise, this next roll is void with no outcome, reset and go onto another roll.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
January 29th, 2024 at 1:53:52 PM
permalink
Quote: TxGammonI am trying to capture values of 0 thru 36 using a pair of dice.
link to original post
You want 37 outcomes with each having a 1/37 change of happening (not 1/36 of happening)?
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
January 29th, 2024 at 2:40:53 PM
permalink
This sounds like something that would best be served by some kind of online random number generator...
January 29th, 2024 at 4:02:42 PM
permalink
Quote: TxGammonI am setting up an experiment using two dice, and I need to account for a 37th outcome which has a 1/36 chance of occurring. For the standard 36 outcomes I am using two dice of different color to differentiate which number occurs on which die. But, how can I capture a 37th outcome? Maybe if the same die values occur on the next roll?
link to original post
Given that 37 is prime, you can't do it with dice that have fewer than 37 sides each.
If you are willing to accept re-rolls, I think the closest you can get with two different 6-sided dice is something like this:
Roll the 2 dice, then roll them again.
If the rolls were different, use the value from the second roll.
If the rolls were the same and NOT 6-6 both times, treat that as the 37th value.
If you rolled four 6s, repeat the entire process.
You can't count two 6-6 rolls as the 37th value as that would mean the 37th value has a probability of 36/1296 while the other 36 each have a probability of only 35/1296.
January 30th, 2024 at 9:19:16 AM
permalink
A possible approach for producing a 37th outcome by rolling two dice, is to roll them multiple times and interpret this sequence of rolls as a number of base 36 which then has to be divided by the multiplier for 37.Quote: TxGammonI am setting up an experiment using two dice, and I need to account for a 37th outcome which has a 1/36 chance of occurring. For the standard 36 outcomes I am using two dice of different color to differentiate which number occurs on which die. But, how can I capture a 37th outcome? Maybe if the same die values occur on the next roll?
link to original post
Procedure
0) Name your standard 36 outcomes 0 through 35, to support modulo calculation.
1) Choose the number of rolls, e.g. 3.
2) Determine the rounded integer multiplier for 37. The first ones are:
1 roll : 36^1 / 37 = 1
2 rolls: 36^2 / 37 = 35
3 rolls: 36^3 / 37 = 1261 (our example)
4 rolls: 36^4 / 37 = 45395
etc.
3) Use Horner's method to calculate the base 10 representation of the base 36 digits rolled (example for three rolls): v = (roll1 * 36 + roll2) * 36 + roll3
4) Divide the value v by the multiplier (corresponding to the number of rolls; for 3 rolls 1261). The integer part is your outcome of any of the 37 values 0 through 36.
This method is not exact but the error in frequency, which corresponds to probability, for the 37th number reduces really quickly with each additional roll:
* -100% for a single roll; the 37th number never appears
* +2.85% for two consecutive rolls; the 37th number appears 36 times instead of 35 times
* -0.079% for three consecutive rolls; 1260 instead of 1261
* +0.002% with four consecutive rolls; 45396 instead of 45395
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
January 31st, 2024 at 6:36:45 AM
permalink
Putting it into practice.
The picture shows the result after the last two rolls, which eventually produced the last number "17" of my experient.
I don't have dice of different colors available, so I chose to roll both dice one after another. (Of course it also works with a single die.)
Another optimization I'm using is, to work in base 6 instead of base 36. The dice already produce digits of base 6, if 1 is subtracted from the value shown.
Horner's method in base 6 for the equivalent of three double-rolls now looks like this:
v = ((((d1 * 6 + d2) * 6 + d3) * 6 + d4) * 6 + d5) * 6 + d6
What seems to be rather complicated at first glance can easily be handled using any basic pocket calculator. The result key "=" will replace the closing parenthesis.
Here is what to type step by step for a single random number out of the 37 values 0 through 36 :
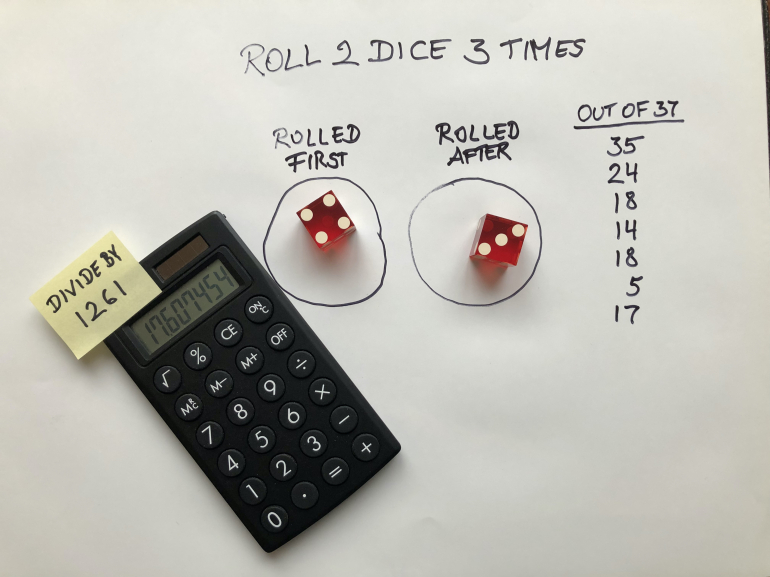The picture shows the result after the last two rolls, which eventually produced the last number "17" of my experient.I don't have dice of different colors available, so I chose to roll both dice one after another. (Of course it also works with a single die.)
Another optimization I'm using is, to work in base 6 instead of base 36. The dice already produce digits of base 6, if 1 is subtracted from the value shown.
die digit
1 0
2 1
3 2
4 3
5 4
6 5
Horner's method in base 6 for the equivalent of three double-rolls now looks like this:
v = ((((d1 * 6 + d2) * 6 + d3) * 6 + d4) * 6 + d5) * 6 + d6
What seems to be rather complicated at first glance can easily be handled using any basic pocket calculator. The result key "=" will replace the closing parenthesis.
Here is what to type step by step for a single random number out of the 37 values 0 through 36 :
type comment
in
C , CE, AC or whatever key clears the calculator's result.
first roll of two dice producing digits d1 and d2
d1 the first die's value minus one
* times
6 the base
+ add
d2 the second die's value minus one
= intermediate sum (indicated by the closing parenthesis in the equation above)
* times
6 the base
+ add
second roll of two dice producing digits d3 and d4
d3 the third die's value minus one
= intermediate sum
* times
6 the base
+ add
d4 the fourth die's value minus one
= intermediate sum
* times
6 the base
+ add
third roll of two dice producing digits d5 and d6
d5 the fifth die's value minus one
= intermediate sum
* times
6 the base
+ add
d6 the sixth die's value minus one
= base 10 representation of the rolled 6-digit number of base 6
/ divide by
1261 the multiplier of 37 for three rolls
= the random number out of 0 through 36 (only use the integer part left to the decimal point as your number)
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
January 31st, 2024 at 7:43:24 AM
permalink
Quote: ThomasK3) Use Horner's method to calculate the base 10 representation of the base 36 digits rolled (example for three rolls): v = (roll1 * 36 + roll2) * 36 + roll3
link to original post
Good post! I am not familiar with Horner's Method, I'll have to read up on it.
I have been thinking of my own method of getting a 1/37 probability using two dice, which may be of different colors. So far I haven't come up with anything. With 37 being prime, I have a feeling it's impossible to get to 1/37 exactly.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 31st, 2024 at 8:06:09 AM
permalink
Quote: TxGammonI am setting up an experiment using two dice, and I need to account for a 37th outcome which has a 1/36 chance of occurring. For the standard 36 outcomes I am using two dice of different color to differentiate which number occurs on which die. But, how can I capture a 37th outcome? Maybe if the same die values occur on the next roll?
link to original post
Not each outcome with 1/37 chance? If this 37th outcome is 1/36 then one or more of the other 36 options need lower probability than 1/36
Are you trying to simulate Euro roulette with two dice?
Psalm 25:16
Turn to me and be gracious to me, for I am lonely and afflicted.
Proverbs 18:2
A fool finds no satisfaction in trying to understand, for he would rather express his own opinion.
January 31st, 2024 at 8:29:43 AM
permalink
You could certainly roll two dice 37 times, leading to 1,332 outcomes and map those into 37 results. More trouble than it’s worth likely.
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
January 31st, 2024 at 11:14:42 AM
permalink
My first thought also was in this direction, until I figured out that one wouldn't get 36*37 but rather 36^37 results.Quote: unJonYou could certainly roll two dice 37 times, leading to 1,332 outcomes and map those into 37 results. More trouble than it’s worth likely.
link to original post
I found this when I tried to reduce the problem to a simpler, even commonly known, one.
Use a fair coin instead of the two dice and thus reduce the 36 possible random outcomes to only 2 still random outcomes.
Toss the coin 8 times instead of 37 times and note heads and tails as 0 and 1.
You now end up with a byte which is well known for having 256 (=2^8) different 8 digit combinations of 0s and 1s.
Now imagine a binary string of length 37. This has 2^37 different 37 digit combinations of 0s and 1s.
In a last step replace back the two dice for the coin. The two dice together produce 36 outcomes. Rolled 37 times, results in 36^37 different 37 digit combinations of 1s through 6s.
And this was when I realized that this is about number systems in different bases.
Fun fact.
Thanks to function "dc" which is the exact(!) desk calculator in Unix operating systems, I'm able to present the above mentioned numbers with all their digits (in base 10, of course):
36*37 = 1,332
2^8 = 256
2^37 = 137,438,953,472
36^37 = 3,829,944,921,253,794,893,077,685,127,088,430,174,646,042,802,674,934,480,896
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
January 31st, 2024 at 11:35:59 AM
permalink
Quote: unJonYou could certainly roll two dice 37 times, leading to 1,332 outcomes and map those into 37 results. More trouble than it’s worth likely.
link to original post
I thought about similar things on my run today. Rolling two dice 37 times leads to 6^74 possible outcomes, if we consider order. 37 will not divide into 6^74 evenly.
You might say that some outcomes result in a re-roll. If we allow that, there are lots of ways to solve the problem and it becomes quiet easy.
For example, roll a single die 37 times. If the first roll is the highest, then you have your 1/37 success. If the first roll is tied for the highest, then you have tie-breaking rounds until there is a winner.
The problem is you could in theory roll forever.
The challenge should be to find a method that always works with a finite number of rolls.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 31st, 2024 at 11:54:32 AM
permalink
Oops that was silly of me.
So roll two dice 5 times. That leads to 36^5 which is divisible by 37.
36^5 = 60,466,176 = 37 * 1,634,221
ETA: fixed typo Wiz caught below.
And that this doesn’t work.
So roll two dice 5 times. That leads to 36^5 which is divisible by 37.
36^5 = 60,466,176 = 37 * 1,634,221
ETA: fixed typo Wiz caught below.
And that this doesn’t work.
Last edited by: unJon on Jan 31, 2024
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
January 31st, 2024 at 11:58:08 AM
permalink
Quote: unJonOops that was silly of me.
So roll two dice 5 times. That leads to 36^5 which is divisible by 37.
36^5 = 604,661,176 = 37 * 1,634,221
link to original post
36^5 = 60,466,176. You have an extra 1 in there.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 31st, 2024 at 11:59:27 AM
permalink
Quote: WizardQuote: unJonOops that was silly of me.
So roll two dice 5 times. That leads to 36^5 which is divisible by 37.
36^5 = 604,661,176 = 37 * 1,634,221
link to original post
36^5 = 60,466,176. You have an extra 1 in there.
link to original post
Thanks for catching. Fixed typo in my post.
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
January 31st, 2024 at 12:38:06 PM
permalink
A general proof might be a nice challenge.Quote: Wizard[...] With 37 being prime, I have a feeling it's impossible to get to 1/37 exactly.
link to original post
For the question, whether there exists any number of rolls of two dice where the number of outcomes could be evenly divided by 37, there might be a first step for an answer.
r ... number of rolls of two dice
m ... the integer multiplier for 37
b ... any base
Number of outcomes of r rolls of two dice should equal a multiple of 37:
36^r = m * 37
Translating it to logarithms:
r * logb 36 = logb m + logb 37
Solving for r, which has to be an integer:
r = logb m / logb 36 + logb 37 / logb 36
Applying the "logarithm's change of base rule" backwards:
r = log36 m + log36 37
It has to be found that integer value "m", that has a log36 which "neutralizes" all decimal places of log36 37 to zero. The integer parts of both logarithms would then add up to the integer number of rolls needed.
I suspect that this does not exist ...
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
January 31st, 2024 at 12:57:14 PM
permalink
Ok one more try at this.
Roll two dice (different color) twice. Leading to 1,296 possible outcomes. If the outcome is all single pips (4 dice show 1s) then all bets push. Take the remaining 1,295 outcomes and map them onto 37 possibilities, as 1,295 / 37 = 35
This is one version of the Wiz answer that you can do this easily if you “allow re-rolls.”
Roll two dice (different color) twice. Leading to 1,296 possible outcomes. If the outcome is all single pips (4 dice show 1s) then all bets push. Take the remaining 1,295 outcomes and map them onto 37 possibilities, as 1,295 / 37 = 35
This is one version of the Wiz answer that you can do this easily if you “allow re-rolls.”
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
January 31st, 2024 at 2:50:40 PM
permalink
or a mechanical device like a spinning wheel with 37 pockets for a ball to drop into.Quote: TigerWuThis sounds like something that would best be served by some kind of online random number generator...
link to original post
"Truth is ever to be found in the simplicity, and not in the multiplicity and confusion of things."
-- Isaac Newton
January 31st, 2024 at 3:56:54 PM
permalink
Quote: ThomasKA general proof might be a nice challenge.Quote: Wizard[...] With 37 being prime, I have a feeling it's impossible to get to 1/37 exactly.
link to original post
For the question, whether there exists any number of rolls of two dice where the number of outcomes could be evenly divided by 37, there might be a first step for an answer.
r ... number of rolls of two dice
m ... the integer multiplier for 37
b ... any base
Number of outcomes of r rolls of two dice should equal a multiple of 37:
36^r = m * 37
link to original post
Quick proof why this is impossible in positive integers:
36^r has only prime factors of 2 and 3, as it is 2^(2r) x 3^(2r),
37 m has 37 as a prime factor.
By the Fundamental Theorem of Arithmetic, given integers a and b > 1, the only way a = b is true is if every prime factor in a appears the same number of times in b, and vice versa.
January 31st, 2024 at 6:24:08 PM
permalink
What if, are two fields where the cubes fall.
And what if you set a condition that a cube of a certain color, with a certain number, must fall into a certain field (for example, a yellow cube with the number six must go into field number one)? + And the second field must contain one of two numbers(for example 1 or 2).
And what if you set a condition that a cube of a certain color, with a certain number, must fall into a certain field (for example, a yellow cube with the number six must go into field number one)? + And the second field must contain one of two numbers(for example 1 or 2).
February 1st, 2024 at 8:40:26 AM
permalink
Thanks, I now understand and like the "re-roll" idea.Quote: unJonOk one more try at this.
Roll two dice (different color) twice. Leading to 1,296 possible outcomes. If the outcome is all single pips (4 dice show 1s) then all bets push. Take the remaining 1,295 outcomes and map them onto 37 possibilities, as 1,295 / 37 = 35
This is one version of the Wiz answer that you can do this easily if you “allow re-rolls.”
link to original post
An interesting fact is, that with any even number of rolls of two dice there is exactly 1 combination too many. Designating exactly one combination for re-rolling will therefore always work.
(An odd number of rolls is missing one cobination in order to be evenly divisible by 37 and therefore is not that well suited for re-rolls.)
Two rolls is the smallest even number and as such the optimal solution to this problem.
For the mapping I advocate the procedure of interpreting the rolled numbers minus 1 as the digits of a four digit value of base 6. This is then translated to base 10 by v = ((d1 * 6 + d2) * 6 + d3) * 6 + d4, using a pocket calculator as shown before. This base 10 number has to be divided by 35, which is the multiplier of 37 for two rolls. The integer part of the result is then one of the 37 values 0 through 36. Each of these numbers is represented by exactly 35 unique combinations of four dice.
The combination for the re-rolls in this case has to be assigned to the dice showing boxcars 6-6-6-6. The corresponding base 10 number is 1295, i.e. the 1296th combination of four base 6 digits, and would correspond to the number 37, which is not in the intended range.
As all even numbers of rolls have exactly 1 combination too many, the freight train is the sign for a re-roll, no matter how long.
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
February 1st, 2024 at 8:42:16 AM
permalink
I somehow knew that number theory would help to prove it.Quote: ThatDonGuyQuote: ThomasKA general proof might be a nice challenge.Quote: Wizard[...] With 37 being prime, I have a feeling it's impossible to get to 1/37 exactly.
link to original post
For the question, whether there exists any number of rolls of two dice where the number of outcomes could be evenly divided by 37, there might be a first step for an answer.
r ... number of rolls of two dice
m ... the integer multiplier for 37
b ... any base
Number of outcomes of r rolls of two dice should equal a multiple of 37:
36^r = m * 37
link to original post
Quick proof why this is impossible in positive integers:
36^r has only prime factors of 2 and 3, as it is 2^(2r) x 3^(2r),
37 m has 37 as a prime factor.
By the Fundamental Theorem of Arithmetic, given integers a and b > 1, the only way a = b is true is if every prime factor in a appears the same number of times in b, and vice versa.
link to original post
Thanks for your explanation and for your fluency in this subject area.
I found another property in this problem:
It can be observed numerically that any even number of rolls has 1 combination too many, while any odd number of rolls is short of 1 combination, in order to be evenly divisible by 37. I fiddled a bit with these two equations but couldn't find a way to prove the proposition:
36^2r = 37 * m + 1
36^(2r+1) = 37 * m - 1
Would you have an idea for an approach?
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
February 1st, 2024 at 6:28:03 PM
permalink
Quote: ThomasKI somehow knew that number theory would help to prove it.Quote: ThatDonGuyQuote: ThomasKA general proof might be a nice challenge.Quote: Wizard[...] With 37 being prime, I have a feeling it's impossible to get to 1/37 exactly.
link to original post
For the question, whether there exists any number of rolls of two dice where the number of outcomes could be evenly divided by 37, there might be a first step for an answer.
r ... number of rolls of two dice
m ... the integer multiplier for 37
b ... any base
Number of outcomes of r rolls of two dice should equal a multiple of 37:
36^r = m * 37
link to original post
Quick proof why this is impossible in positive integers:
36^r has only prime factors of 2 and 3, as it is 2^(2r) x 3^(2r),
37 m has 37 as a prime factor.
By the Fundamental Theorem of Arithmetic, given integers a and b > 1, the only way a = b is true is if every prime factor in a appears the same number of times in b, and vice versa.
link to original post
Thanks for your explanation and for your fluency in this subject area.
I found another property in this problem:
It can be observed numerically that any even number of rolls has 1 combination too many, while any odd number of rolls is short of 1 combination, in order to be evenly divisible by 37. I fiddled a bit with these two equations but couldn't find a way to prove the proposition:
36^2r = 37 * m + 1
36^(2r+1) = 37 * m - 1
Would you have an idea for an approach?
link to original post
Remember that a^b - 1 = (a - 1) (1 + a + a^2 + ... + a^(b-1))
For even:
36^(2r) - 1 = (36^2)^r - 1 = 1296^r - 1
= (1296 - 1)(1 + 1296 + 1296^2 + ... + 1296^(r-1))
= 37 * (35 * (1 + 1296 + 1296^2 + ... + 1296^(r-1)))
Add 1 to both sides:
36^(2r) = 37 * (35 * (1 + 1296 + 1296^2 + ... + 1296^(r-1))) + 1
For odd:
36^(2r+1) = 36 * 36^(2r)
= 36 * (37 * (35 * (1 + 1296 + 1296^2 + ... + 1296^(r-1))) + 1)
= 36 * 37 * (35 * (1 + 1296 + 1296^2 + ... + 1296^(r-1))) + (37 - 1)
= 37 * (36 * (35 * (1 + 1296 + 1296^2 + ... + 1296^(r-1))) + 1) - 1
February 2nd, 2024 at 3:46:14 AM
permalink
Quote: TxGammonAre the odds 1/36 if I have a blue die that rolls a 3 and a yellow die that rolls a 2, then the same outcome occurs on the next roll?
link to original post
Pretty sure the odds of that with specific colors are 1/36 * 1/36 if the dice are fair.
Chances regardless of color of that roll would be 1/18 * 1/18.
Chances of the total of 5 pips would be 1/9 * 1/9, to include the 4-1.
If you roll the dice, the event happened, so imo no place for the zero there.
However, a 37th (zero) event could be fouled dice, with one or both stacked, cocked, or off the table. A person could perhaps bet on that except it's pretty easy to throw one off intentionally.
ETA: What TDG said.
If the House lost every hand, they wouldn't deal the game.
February 2nd, 2024 at 6:21:19 AM
permalink
Just out of curiosity I thought about a solution for double-zero roulette lovers.
As in the 37-case only two rolls of a pair of dice are necessary.
The base 10 representation has now to be divided by 34 to produce the 38 values 0 through 37.
The last four combinations produce the number 38 and therefore are the re-roll indicators:
6-6-6-3
6-6-6-4
6-6-6-5
6-6-6-6
For double-zero roulette the number 37 would represent 00, all other numbers stand for themselves.
For completeness, triple-zero roulette:
Two rolls of a pair of dice.
The divisor is 33.
The 9 (nine) re-roll indicators (Number 39) are
6-6-5-4
6-6-5-5
6-6-5-6
6-6-6-1
6-6-6-2
6-6-6-3
6-6-6-4
6-6-6-5
6-6-6-6
Representations:
0 --> 0
37 --> 00
38 --> 000
As in the 37-case only two rolls of a pair of dice are necessary.
The base 10 representation has now to be divided by 34 to produce the 38 values 0 through 37.
The last four combinations produce the number 38 and therefore are the re-roll indicators:
6-6-6-3
6-6-6-4
6-6-6-5
6-6-6-6
For double-zero roulette the number 37 would represent 00, all other numbers stand for themselves.
For completeness, triple-zero roulette:
Two rolls of a pair of dice.
The divisor is 33.
The 9 (nine) re-roll indicators (Number 39) are
6-6-5-4
6-6-5-5
6-6-5-6
6-6-6-1
6-6-6-2
6-6-6-3
6-6-6-4
6-6-6-5
6-6-6-6
Representations:
0 --> 0
37 --> 00
38 --> 000
"When it comes to probability and statistics, intuition is a bad advisor. Don't speculate. Calculate." - a math textbook author (name not recalled)
March 9th, 2024 at 10:00:40 AM
permalink
Roll together a 6-sided die and an 8-sided die. This gives 48 possible outcomes. Now designate 11 of those outcomes as bad rolls that result in an automatic re-roll. Then you get 37 valid rolls, each with an equal probability of occurring. There is the infinitesimal chance that you roll a bad roll infinity times in a row.
