Round Robin Scheduling
December 10th, 2023 at 3:13:07 PM
permalink
I was recently asked to set up a round robin schedule for a shuffleboard tournament. It was a topic I've never thought much about before, but looked into it the last couple days and will write about where I'm at so far over the next few posts.
Before I go further, a round robin is a tournament format where everybody plays everybody. Whoever gets the most individual wins, wins the entire tournament. Ideally, you want to break the tournament into rounds where everybody plays each round.
First, let's start with the simple situation of you have an even number of players and there is no advantage to either side in a game. Later, we will get into how to deal with one side having an advantage, like in tennis, where you don't want the sun in your eyes.
Let's take the case of 8 players. Label them A to H. Round 1 will have the following four matches, as shown in the four rectangles.
After the four games are played, player A stays in the same position and everybody else rotates, as follows.
After the rotation, round 2 will have these match-ups.
Then, rotate again, in the same manner as before. It works out that everybody will play everybody. Here is a table showing all the individual match-ups.
Note: Table corrected
I'll pause for comments and questions at this point. Then, I'll explain how to deal with an odd number of players.
Before I go further, a round robin is a tournament format where everybody plays everybody. Whoever gets the most individual wins, wins the entire tournament. Ideally, you want to break the tournament into rounds where everybody plays each round.
First, let's start with the simple situation of you have an even number of players and there is no advantage to either side in a game. Later, we will get into how to deal with one side having an advantage, like in tennis, where you don't want the sun in your eyes.
Let's take the case of 8 players. Label them A to H. Round 1 will have the following four matches, as shown in the four rectangles.
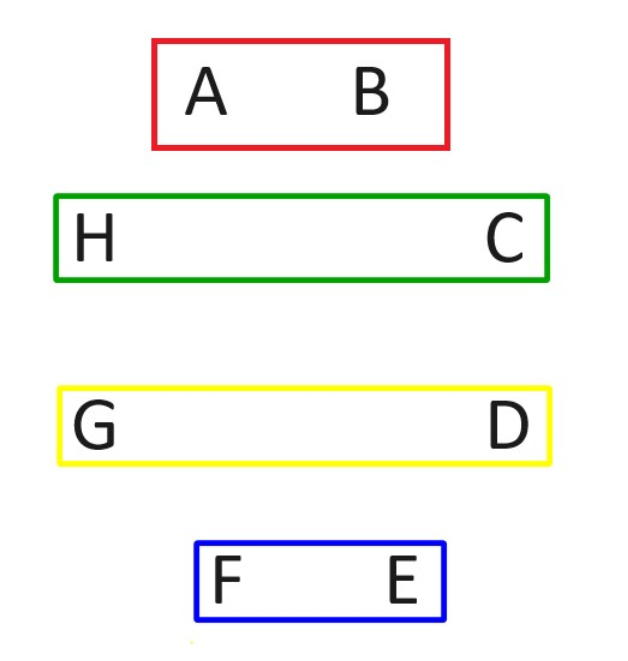
After the four games are played, player A stays in the same position and everybody else rotates, as follows.
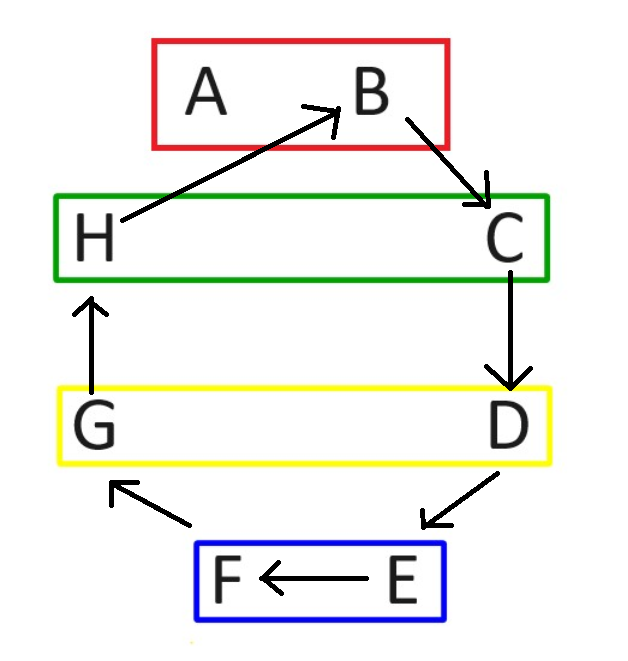
After the rotation, round 2 will have these match-ups.
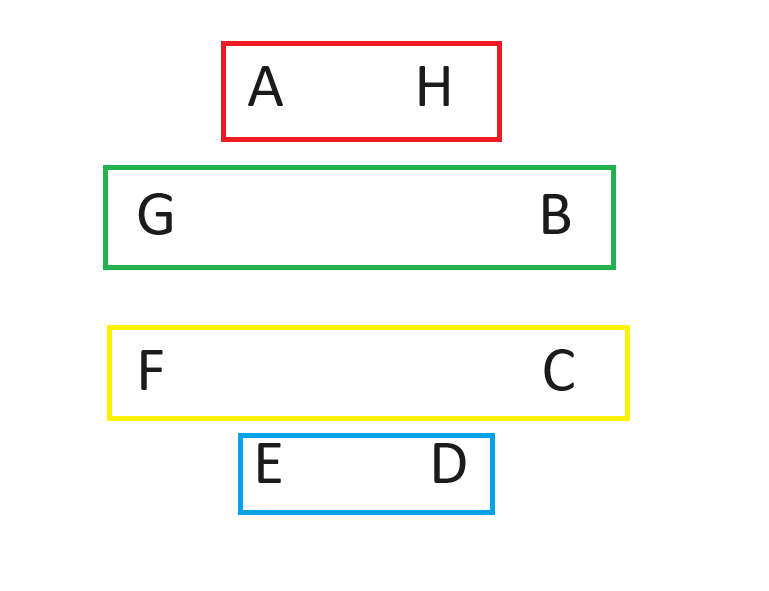
Then, rotate again, in the same manner as before. It works out that everybody will play everybody. Here is a table showing all the individual match-ups.
| Round | Player 1 | Player 2 |
|---|---|---|
| 1 | A | B |
| 1 | H | C |
| 1 | G | D |
| 1 | F | E |
| 2 | A | H |
| 2 | G | B |
| 2 | F | C |
| 2 | E | D |
| 3 | A | G |
| 3 | F | H |
| 3 | E | B |
| 3 | D | C |
| 4 | A | F |
| 4 | E | G |
| 4 | D | H |
| 4 | C | B |
| 5 | A | E |
| 5 | D | F |
| 5 | C | G |
| 5 | B | H |
| 6 | A | D |
| 6 | C | E |
| 6 | B | F |
| 6 | H | G |
| 7 | A | C |
| 7 | B | D |
| 7 | H | E |
| 7 | G | F |
Note: Table corrected
I'll pause for comments and questions at this point. Then, I'll explain how to deal with an odd number of players.
Last edited by: Wizard on Dec 10, 2023
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 10th, 2023 at 3:37:42 PM
permalink
I'm a little confused.
B plays C in round 2, again in round 4, and again in round 6.
H plays B in rounds 3, 5 and 7.
D vs E in rounds 2, 4 and 7.
Etc.
B plays C in round 2, again in round 4, and again in round 6.
H plays B in rounds 3, 5 and 7.
D vs E in rounds 2, 4 and 7.
Etc.
Have you tried 22 tonight? I said 22.
December 10th, 2023 at 4:09:13 PM
permalink
What is the goal? You are obviously not trying to minimize the number of teams that move. Maybe you are trying to minimize the distance traveled.
My algorithm: Lowest letter that is unscheduled plays the lowest letter they have not already played. Repeat until the tournament ends.
My algorithm: Lowest letter that is unscheduled plays the lowest letter they have not already played. Repeat until the tournament ends.
This forum is more enjoyable after I learned how to use the 'Block this user' button.
December 10th, 2023 at 4:18:15 PM
permalink
Quote: GialmereI'm a little confused.
B plays C in round 2, again in round 4, and again in round 6.
H plays B in rounds 3, 5 and 7.
D vs E in rounds 2, 4 and 7.
Etc.
link to original post
You're absolutely right. I made a mistake in creating the table in Excel. It has been fixed. Notice how the positions rotate in each round in a clockwise manner, excluding the upper left position.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 10th, 2023 at 4:22:59 PM
permalink
Quote: MentalWhat is the goal? You are obviously not trying to minimize the number of teams that move. Maybe you are trying to minimize the distance traveled.
The goal is to have everybody play at as regular intervals as possible. In the case of eight players and four courts, or any situation where the courts*2 = players you can have everybody playing at the same time. Even if you have only one court, everybody will play at fairly regular intervals, once somewhere in every four matches.
Quote:My algorithm: Lowest letter that is unscheduled plays the lowest letter they have not already played. Repeat until the tournament ends.
link to original post
That will work, but the players with the low letters will be playing a lot at the beginning while the players at the end will play mostly at the end. I want to minimize the longest breaks between games if there is only one court and keep everybody playing if the number of courts >= players/2.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 10th, 2023 at 4:23:25 PM
permalink
Quote: WizardI'll pause for comments and questions at this point. Then, I'll explain how to deal with an odd number of players.
link to original post
Er, you are aware that B is playing C in rounds 2, 4, and 6, right?
(OOPS - in the time it took for me to say that, you made your edit...)
I have a method for calculating round robin - as soon as I can format it, I'll present it.
December 10th, 2023 at 4:33:20 PM
permalink
Another variable is how many shuffleboard tables do you have?
If you have only one table, that would be a factor because
I noticed in your table that A gets to play the tournament with 3 matches between each round of play, whereas E and F have several rounds of only 2 matches to rest, then a couple periods where they have 4 rounds where they have to wait.
I haven't thought about this enough to know whether this situation can be prevented based on the number of entrants, but fair competition does need to account for rest between matches while also not giving too much rest and allowing someone to get "rusty" vs someone who has an even amount of competition rest/action.
If you have only one table, that would be a factor because
I noticed in your table that A gets to play the tournament with 3 matches between each round of play, whereas E and F have several rounds of only 2 matches to rest, then a couple periods where they have 4 rounds where they have to wait.
I haven't thought about this enough to know whether this situation can be prevented based on the number of entrants, but fair competition does need to account for rest between matches while also not giving too much rest and allowing someone to get "rusty" vs someone who has an even amount of competition rest/action.
December 10th, 2023 at 4:46:34 PM
permalink
Quote: ThatDonGuyI have a method for calculating round robin - as soon as I can format it, I'll present it.
link to original post
And here it is:
How to do a 10-player round robin:
Work backwards.
10 is 2 groups of 5
5 is 2 groups of 2 plus 1, so make it 2 groups of 3
3 is 1 group of 2 plus 1, so make it 2 groups of 2
In each table, the player in the first column plays the players in the remaining columns in each round.
Start with a group of 2 - this is trivial:
| 1 | 2 |
| 2 | 1 |
Now, duplicate that group into two groups of 2:
| 1 | 2 |
| 2 | 1 |
| 3 | 4 |
| 4 | 3 |
Each player in the first group plays each player in the second group:
| 1 | 2 | 3 | 4 |
| 2 | 1 | 4 | 3 |
| 3 | 4 | 1 | 2 |
| 4 | 3 | 2 | 1 |
However, there are only 3 players in the group, so remove the row for player 4, and replace 4 with 0 (which indicates a bye):
| 1 | 2 | 3 | 0 |
| 2 | 1 | 0 | 3 |
| 3 | 0 | 1 | 2 |
To create a group of 5, first create a second group of 3, and again, have every player in the first group play every player in the second group:
| 1 | 2 | 3 | 0 | 4 | 5 | 6 |
| 2 | 1 | 0 | 3 | 5 | 6 | 4 |
| 3 | 0 | 1 | 2 | 6 | 4 | 5 |
| 4 | 5 | 6 | 0 | 1 | 2 | 3 |
| 5 | 4 | 0 | 5 | 2 | 3 | 1 |
| 6 | 0 | 4 | 6 | 3 | 1 | 2 |
You will notice that, in each of the first three columns, there is a player in the first group and their "matching" player in the second group that have byes.
Replace the byes with these players playing each other. You can now remove the column where they play each other.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 1 | 5 | 3 | 6 | 4 |
| 3 | 6 | 1 | 2 | 4 | 5 |
| 4 | 5 | 6 | 1 | 2 | 3 |
| 5 | 4 | 2 | 6 | 3 | 1 |
| 6 | 3 | 4 | 5 | 1 | 2 |
However, since you only want a group of 5, remove Player 6:
| 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 1 | 5 | 3 | 0 | 4 |
| 3 | 0 | 1 | 2 | 4 | 5 |
| 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 4 | 2 | 0 | 3 | 1 |
Now, create a second group of 5:
| 1 | 2 | 3 | 4 | 5 | 0 | 6 | 7 | 8 | 9 | 10 |
| 2 | 1 | 5 | 3 | 0 | 4 | 7 | 8 | 9 | 10 | 6 |
| 3 | 0 | 1 | 2 | 4 | 5 | 8 | 9 | 10 | 6 | 7 |
| 4 | 5 | 0 | 1 | 2 | 3 | 9 | 10 | 6 | 7 | 8 |
| 5 | 4 | 2 | 0 | 3 | 1 | 10 | 6 | 7 | 8 | 9 |
| 6 | 7 | 8 | 9 | 10 | 0 | 1 | 5 | 4 | 3 | 2 |
| 7 | 6 | 10 | 8 | 0 | 9 | 2 | 1 | 5 | 4 | 3 |
| 8 | 0 | 6 | 7 | 9 | 5 | 3 | 2 | 1 | 5 | 4 |
| 9 | 10 | 0 | 6 | 7 | 8 | 4 | 3 | 2 | 1 | 5 |
| 10 | 9 | 7 | 0 | 8 | 6 | 5 | 4 | 3 | 2 | 1 |
Again, match the byes, and remove the column that has them paired:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 1 | 5 | 3 | 7 | 4 | 8 | 9 | 10 | 6 |
| 3 | 8 | 1 | 2 | 4 | 5 | 9 | 10 | 6 | 7 |
| 4 | 5 | 9 | 1 | 2 | 3 | 10 | 6 | 7 | 8 |
| 5 | 4 | 2 | 10 | 3 | 1 | 6 | 7 | 8 | 9 |
| 6 | 7 | 8 | 9 | 10 | 1 | 5 | 4 | 3 | 2 |
| 7 | 6 | 10 | 8 | 2 | 9 | 1 | 5 | 4 | 3 |
| 8 | 3 | 6 | 7 | 9 | 5 | 2 | 1 | 5 | 4 |
| 9 | 10 | 4 | 6 | 7 | 8 | 3 | 2 | 1 | 5 |
| 10 | 9 | 7 | 5 | 8 | 6 | 4 | 3 | 2 | 1 |
Oh, and the answer to "how do you handle an odd number" is, add a person called "Bye" - whoever plays Bye gets a bye in that round.
Also, you need to change the image - the pairings go across, by "row", and not the way you have them.
December 10th, 2023 at 4:58:48 PM
permalink
Okay, Your diagram seemed to indicate four courts and four simultaneous games. My algorithm assumes four games scheduled prior to each round. Everyone plays in every round.
This forum is more enjoyable after I learned how to use the 'Block this user' button.
December 10th, 2023 at 5:09:09 PM
permalink
Quote: ThatDonGuy
Also, you need to change the image - the pairings go across, by "row", and not the way you have them.
link to original post
What you want is this - this matches your table:
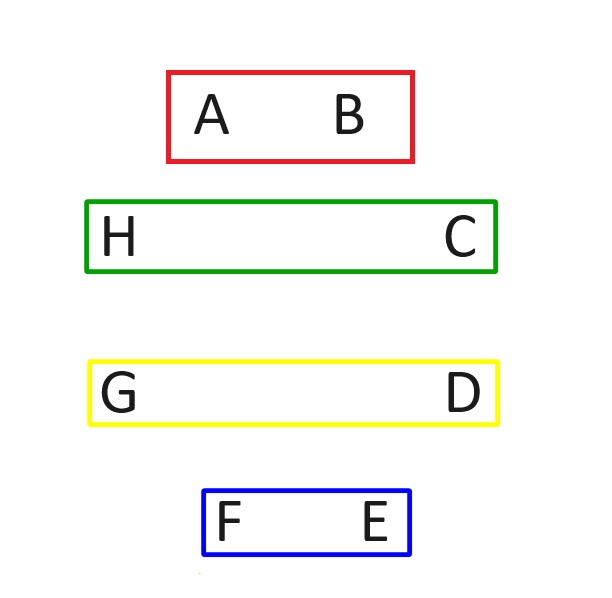
Keep the rotation the same - B to C to D to E to F to G to H to B.
I think I have a proof that this works, although it's not as rigorous as I would like:
Put the players into two rows
Row 1: 1, 2, 3, ..., n-1, n
Row 2: 2n, 2n-1, 2n-2, ..., n+2, n+1
For each subsequent round, rotate 2 through 2n clockwise.
Player 1 will play, in order, 2n, 2n-1, 2n-2, and so on through 2.
For, say, Player 2, note that Player 2's first opponent is 2n-1; the difference is an odd number. Call this "odd parity".
In each of the next n-2 rounds, player 2 moves "forward" one space, and the number of player 2's new opponent will be one less than their previous opponent, so the difference will change by 2, keeping the odd parity.
When 2 moves from the top row to the bottom, the opponent changes from 3 to 2n; since the difference is odd, the parity changes from odd to even.
The parity will remain even as 2 remains on the bottom row, until all of the opponents have been played.
Note that, for player 3, when 3 moves from the far left of the bottom row to the second spot on the top row, the opponent changes from 1 to 2n, switching the parity again.
December 10th, 2023 at 6:59:12 PM
permalink
Quote: ThatDonGuyWhat you want is this - this matches your table:
link to original post
Thank you. You're right, as usual.
Please give me some time to digest your other comments.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 11th, 2023 at 8:02:39 AM
permalink
Somebody else already mentioned this, but here is the solution for an odd number of players. You simply replace add a "bye" to the list of players and then treat it as an even number. For example, with seven players, you add one to get eight. The player who goes against the "bye" gets to rest that round. Here is the table for 7 players. In this case, I replaced player H.
| Round | Player 1 | Player 2 |
|---|---|---|
| 1 | A | B |
| 1 | bye | C |
| 1 | G | D |
| 1 | F | E |
| 2 | A | bye |
| 2 | G | B |
| 2 | F | C |
| 2 | E | D |
| 3 | A | G |
| 3 | F | bye |
| 3 | E | B |
| 3 | D | C |
| 4 | A | F |
| 4 | E | G |
| 4 | D | bye |
| 4 | C | B |
| 5 | A | E |
| 5 | D | F |
| 5 | C | G |
| 5 | B | bye |
| 6 | A | D |
| 6 | C | E |
| 6 | B | F |
| 6 | bye | G |
| 7 | A | C |
| 7 | B | D |
| 7 | bye | E |
| 7 | G | F |
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 11th, 2023 at 8:15:35 AM
permalink
I am still not understanding what you are looking for here. It is trivial to get the list of RR matches and there are very many solutions to scheduling those matches in rounds.Quote: WizardSomebody else already mentioned this, but here is the solution for an odd number of players. You simply replace add a "bye" to the list of players and then treat it as an even number. For example, with seven players, you add one to get eight. The player who goes against the "bye" gets to rest that round. Here is the table for 7 players. In this case, I replaced player H.
Round Player 1 Player 2 1 A B 1 bye C 1 G D 1 F E 2 A bye 2 G B 2 F C 2 E D 3 A G 3 F bye 3 E B 3 D C 4 A F 4 E G 4 D bye 4 C B 5 A E 5 D F 5 C G 5 B bye 6 A D 6 C E 6 B F 6 bye G 7 A C 7 B D 7 bye E 7 G F
link to original post
What is the criteria that makes one solution better than another solution? The only criteria I see in the OP is that nobody should play twice in a round.
Are you just looking for an elegant algorithm to generate one acceptable solution?
This forum is more enjoyable after I learned how to use the 'Block this user' button.
December 11th, 2023 at 9:28:56 AM
permalink
I wonder . . .
Supposing it was a three person game? Such as three player pinochle? Or any 3-player board game?
Simple case: Let's say you have 6 players total. You want to create a round robin tourny in which there are 10 rounds of two games with each game involving a threesome of players.
- Each player must play a match against every possible combination of two players (with no repeating.)
Is there an analogue to the rotation method that Wizard has identified to define the ten rounds -(understanding that there is no preferred sequence to the rounds?)
This question becomes harder when there are 9 players, and 28 rounds of three simultaneous games of three players each.
Supposing it was a three person game? Such as three player pinochle? Or any 3-player board game?
Simple case: Let's say you have 6 players total. You want to create a round robin tourny in which there are 10 rounds of two games with each game involving a threesome of players.
- Each player must play a match against every possible combination of two players (with no repeating.)
Is there an analogue to the rotation method that Wizard has identified to define the ten rounds -(understanding that there is no preferred sequence to the rounds?)
This question becomes harder when there are 9 players, and 28 rounds of three simultaneous games of three players each.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
December 11th, 2023 at 12:26:37 PM
permalink
Quote: gordonm888I wonder . . .
Supposing it was a three person game? Such as three player pinochle? Or any 3-player board game?
link to original post
Good question. Off hand, I don't have an answer.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 11th, 2023 at 1:08:16 PM
permalink
I know there's a beautifully convoluted scheme the family uses for the annual euchre tournament.
This is a four player game, with partners changing after each round, and different pairs of partners changing tables every other round.
(There is some favoritism built into the rotation. Somehow, Grandma never has to move seats, because she doesn't walk so well... but somehow everyone plays with everyone, and everyone plays against everyone.)
This is a four player game, with partners changing after each round, and different pairs of partners changing tables every other round.
(There is some favoritism built into the rotation. Somehow, Grandma never has to move seats, because she doesn't walk so well... but somehow everyone plays with everyone, and everyone plays against everyone.)
May the cards fall in your favor.
December 11th, 2023 at 1:23:49 PM
permalink
In my OP I stated I would get to a away to assign sides of a court so that each player had the good side an equal number of times as the bad side. As an example where this might be applicable is in tennis, where one side has the sun in his eyes.
My method is a modified Lizard Spock expansion, which is a way of playing rock-paper-scissors with any odd number of symbols greater than 1.
Direct: https://www.youtube.com/watch?v=0-KMH02Mauk
Let's look at a seven-player round robin.
The arrow points from the player getting the good side to the player getting the bad side.
Another way to think about it is to arrange the players names in a circle. Consider the fewest steps between any two players. The player with the side advantage is the one who is the fewest steps away from the other player going CLOCKWISE.
First, consider a match between B and D. Those players are 2 steps apart. Player B is the one is 2 steps from D going clockwise, so B gets the side advantage.
Second, consider a match between C and G. They are 3 steps apart. Player G is the one is 3 steps from C going clockwise, so G gets the side advantage.
The following table shows the match-ups including side advantage.
I suppose you could employ this with an even number of players, except it doesn't work if the players are half way across the circle from each other. In that case, you would have to randomize.
My method is a modified Lizard Spock expansion, which is a way of playing rock-paper-scissors with any odd number of symbols greater than 1.
Direct: https://www.youtube.com/watch?v=0-KMH02Mauk
Let's look at a seven-player round robin.
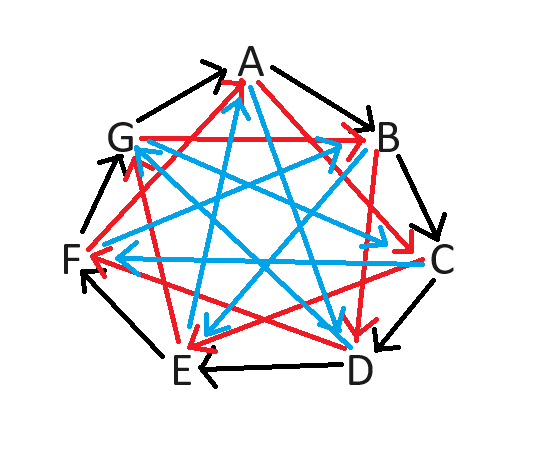
The arrow points from the player getting the good side to the player getting the bad side.
Another way to think about it is to arrange the players names in a circle. Consider the fewest steps between any two players. The player with the side advantage is the one who is the fewest steps away from the other player going CLOCKWISE.
First, consider a match between B and D. Those players are 2 steps apart. Player B is the one is 2 steps from D going clockwise, so B gets the side advantage.
Second, consider a match between C and G. They are 3 steps apart. Player G is the one is 3 steps from C going clockwise, so G gets the side advantage.
The following table shows the match-ups including side advantage.
| Round | Player 1 | Player 2 | Side advantage |
|---|---|---|---|
| 1 | A | B | A |
| 1 | bye | C | |
| 1 | G | D | D |
| 1 | F | E | E |
| 2 | A | bye | |
| 2 | G | B | G |
| 2 | F | C | C |
| 2 | E | D | D |
| 3 | A | G | G |
| 3 | F | bye | |
| 3 | E | B | B |
| 3 | D | C | C |
| 4 | A | F | F |
| 4 | E | G | E |
| 4 | D | bye | |
| 4 | C | B | B |
| 5 | A | E | E |
| 5 | D | F | D |
| 5 | C | G | G |
| 5 | B | bye | |
| 6 | A | D | A |
| 6 | C | E | C |
| 6 | B | F | F |
| 6 | bye | G | |
| 7 | A | C | A |
| 7 | B | D | B |
| 7 | bye | E | |
| 7 | G | F | F |
I suppose you could employ this with an even number of players, except it doesn't work if the players are half way across the circle from each other. In that case, you would have to randomize.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 11th, 2023 at 1:37:36 PM
permalink
A tennis match is comprised of multiple games with the players switching sides often. Shuffle board doesn’t do that?
"Truth is ever to be found in the simplicity, and not in the multiplicity and confusion of things."
-- Isaac Newton
December 12th, 2023 at 6:02:01 PM
permalink
Quote: JimRockfordA tennis match is comprised of multiple games with the players switching sides often. Shuffle board doesn’t do that?
link to original post
Is there changing sides in a single game of, say, cornhole, or horseshoes?
Update: in cornhole, if it's singles, they do change ends after each round; if it's doubles, they stay where they are for the entire game.
December 12th, 2023 at 7:09:52 PM
permalink
In tennis, players switch sides after every odd-numbered game. So, that was not the best example of a home-side advantage.
The project I was challenged to do was to configure a 25-player shuffleboard tournament with six courts where every court had two sides. I was able break it evenly into four courts or two sides, but not both. While I failed at the task, it at least gave me something to think and write about.
If anyone else can solve the challenge, the one who asked promised to give a donation to Three Square food bank of at least $100. You'll also humble me if you can do it.
The project I was challenged to do was to configure a 25-player shuffleboard tournament with six courts where every court had two sides. I was able break it evenly into four courts or two sides, but not both. While I failed at the task, it at least gave me something to think and write about.
If anyone else can solve the challenge, the one who asked promised to give a donation to Three Square food bank of at least $100. You'll also humble me if you can do it.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 13th, 2023 at 6:43:44 AM
permalink
Quote: WizardIn tennis, players switch sides after every odd-numbered game. So, that was not the best example of a home-side advantage.
I thought in tennis they switched sides after every sixth game.
At my age, a "Life In Prison" sentence is not much of a deterrent.
December 13th, 2023 at 7:05:13 PM
permalink
Quote: DRichQuote: WizardIn tennis, players switch sides after every odd-numbered game. So, that was not the best example of a home-side advantage.
I thought in tennis they switched sides after every sixth game.
link to original post
No - change sides every other game (or, in a tiebreak, after every six points), starting with the second game of the match.
Usually, balls are changed after the first seven games, and then every nine games after that.
December 13th, 2023 at 7:06:40 PM
permalink
Quote: WizardThe project I was challenged to do was to configure a 25-player shuffleboard tournament with six courts where every court had two sides. I was able break it evenly into four courts or two sides, but not both. While I failed at the task, it at least gave me something to think and write about.
link to original post
When you say "every court has two sides," does this allow for 12 games to be played "at once", with each court hosting two games?
Meanwhile, here is a solution to the 9-player, 3-handed-game round robin schedule - it was a brute force implementation, but maybe somebody can spot a pattern to come up with an algorithm:
| 1,2,3 | 4,5,6 | 7,8,9 |
| 1,2,4 | 3,5,7 | 6,8,9 |
| 1,2,5 | 3,4,8 | 6,7,9 |
| 1,2,6 | 3,4,7 | 5,8,9 |
| 1,2,7 | 3,4,9 | 5,6,8 |
| 1,2,8 | 3,4,6 | 5,7,9 |
| 1,2,9 | 3,4,5 | 6,7,8 |
| 1,3,4 | 2,6,9 | 5,7,8 |
| 1,3,5 | 2,6,7 | 4,8,9 |
| 1,3,6 | 2,5,8 | 4,7,9 |
| 1,3,7 | 2,4,8 | 5,6,9 |
| 1,3,8 | 2,5,7 | 4,6,9 |
| 1,3,9 | 2,6,8 | 4,5,7 |
| 1,4,5 | 2,7,8 | 3,6,9 |
| 1,4,6 | 2,7,9 | 3,5,8 |
| 1,4,7 | 2,8,9 | 3,5,6 |
| 1,4,8 | 2,5,9 | 3,6,7 |
| 1,4,9 | 2,5,6 | 3,7,8 |
| 1,5,6 | 2,3,9 | 4,7,8 |
| 1,5,7 | 2,4,9 | 3,6,8 |
| 1,5,8 | 2,4,6 | 3,7,9 |
| 1,5,9 | 2,3,8 | 4,6,7 |
| 1,6,7 | 2,4,5 | 3,8,9 |
| 1,6,8 | 2,4,7 | 3,5,9 |
| 1,6,9 | 2,3,7 | 4,5,8 |
| 1,7,8 | 2,3,6 | 4,5,9 |
| 1,7,9 | 2,3,5 | 4,6,8 |
| 1,8,9 | 2,3,4 | 5,6,7 |
December 13th, 2023 at 7:56:58 PM
permalink
Quote: ThatDonGuyWhen you say "every court has two sides," does this allow for 12 games to be played "at once", with each court hosting two games?
link to original post
In the original task posed to me, time doesn't matter. 12 games can or cannot be played at once, it doesn't matter.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 14th, 2023 at 1:23:56 PM
permalink
Quote: ThatDonGuyQuote: WizardThe project I was challenged to do was to configure a 25-player shuffleboard tournament with six courts where every court had two sides. I was able break it evenly into four courts or two sides, but not both. While I failed at the task, it at least gave me something to think and write about.
link to original post
When you say "every court has two sides," does this allow for 12 games to be played "at once", with each court hosting two games?
Meanwhile, here is a solution to the 9-player, 3-handed-game round robin schedule - it was a brute force implementation, but maybe somebody can spot a pattern to come up with an algorithm:
1,2,3 4,5,6 7,8,9 1,2,4 3,5,7 6,8,9 1,2,5 3,4,8 6,7,9 1,2,6 3,4,7 5,8,9 1,2,7 3,4,9 5,6,8 1,2,8 3,4,6 5,7,9 1,2,9 3,4,5 6,7,8 1,3,4 2,6,9 5,7,8 1,3,5 2,6,7 4,8,9 1,3,6 2,5,8 4,7,9 1,3,7 2,4,8 5,6,9 1,3,8 2,5,7 4,6,9 1,3,9 2,6,8 4,5,7 1,4,5 2,7,8 3,6,9 1,4,6 2,7,9 3,5,8 1,4,7 2,8,9 3,5,6 1,4,8 2,5,9 3,6,7 1,4,9 2,5,6 3,7,8 1,5,6 2,3,9 4,7,8 1,5,7 2,4,9 3,6,8 1,5,8 2,4,6 3,7,9 1,5,9 2,3,8 4,6,7 1,6,7 2,4,5 3,8,9 1,6,8 2,4,7 3,5,9 1,6,9 2,3,7 4,5,8 1,7,8 2,3,6 4,5,9 1,7,9 2,3,5 4,6,8 1,8,9 2,3,4 5,6,7
link to original post
Great. I had tried a manual search and got this far, but then there was no possible solution for the round that started with ADI or 1,4,9. So, it is very possible to have branches that are not viable.
| A | B | C | D | E | F | G | H | I | ||
| A | B | D | C | E | G | F | H | I | ||
| A | B | E | C | D | H | F | G | I | ||
| A | B | F | C | D | G | E | H | I | ||
| A | B | G | C | D | I | E | F | H | ||
| A | B | H | C | D | F | E | G | I | ||
| A | B | I | C | D | E | F | G | H | ||
| A | C | D | B | F | I | E | G | H | ||
| A | C | E | B | F | G | D | H | I | ||
| A | C | F | B | E | H | D | G | I | ||
| A | C | G | B | D | H | E | F | I | ||
| A | C | H | B | D | I | E | F | G | ||
| A | C | I | B | E | G | D | G | H | ||
| A | D | E | B | F | H | C | G | I | ||
| A | D | F | B | E | I | C | G | H | ||
| A | D | G | B | E | F | C | H | I | ||
| A | D | H | B | G | I | C | E | F | ||
Our two attempts are the same up until your row 1,3,7__ 2,4,8__5,6,9 but on the next row I tried a different option than you and I eventually crashed and burned on the row that starts 1,4,9.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
December 14th, 2023 at 4:19:28 PM
permalink
Quote: WizardQuote: GialmereI'm a little confused.
B plays C in round 2, again in round 4, and again in round 6.
H plays B in rounds 3, 5 and 7.
D vs E in rounds 2, 4 and 7.
Etc.
link to original post
You're absolutely right. I made a mistake in creating the table in Excel. It has been fixed. Notice how the positions rotate in each round in a clockwise manner, excluding the upper left position.
link to original post
Standard Howell movement in Duplicate bridge.
December 14th, 2023 at 4:28:45 PM
permalink
Quote: WizardIn tennis, players switch sides after every odd-numbered game. So, that was not the best example of a home-side advantage.
The project I was challenged to do was to configure a 25-player shuffleboard tournament with six courts where every court had two sides. I was able break it evenly into four courts or two sides, but not both. While I failed at the task, it at least gave me something to think and write about.
If anyone else can solve the challenge, the one who asked promised to give a donation to Three Square food bank of at least $100. You'll also humble me if you can do it.
link to original post
I don’t understand the question. 25 players. 6 shuffleboard courts? 2 people or 4 people (in 2 teams of 2) play at once? And you just need everyone to play everyone else (and with everyone else if teams)?
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
December 14th, 2023 at 4:57:19 PM
permalink
Quote: WizardQuote: ThatDonGuyWhen you say "every court has two sides," does this allow for 12 games to be played "at once", with each court hosting two games?
link to original post
In the original task posed to me, time doesn't matter. 12 games can or cannot be played at once, it doesn't matter.
link to original post
I am confused. Why doesn't this work:
The six courts are A through F; either the games marked A1 through F1 in a round are played, and then A2 through F2, or the A1-F1 games are played from one side of the court and A2-F2 are simultaneously played from the other
| Bye | A 1 | B 1 | C 1 | D 1 | E 1 | F 1 | A 2 | B 2 | C 2 | D 2 | E 2 | F 2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 1 - 24 | 2 - 23 | 3 - 22 | 4 - 21 | 5 - 20 | 6 - 19 | 7 - 18 | 8 - 17 | 9 - 16 | 10 - 15 | 11 - 14 | 12 - 13 |
| 24 | 25 - 23 | 1 - 22 | 2 - 21 | 3 - 20 | 4 - 19 | 5 - 18 | 6 - 17 | 7 - 16 | 8 - 15 | 9 - 14 | 10 - 13 | 11 - 12 |
| 23 | 24 - 22 | 25 - 21 | 1 - 20 | 2 - 19 | 3 - 18 | 4 - 17 | 5 - 16 | 6 - 15 | 7 - 14 | 8 - 13 | 9 - 12 | 10 - 11 |
| 22 | 23 - 21 | 24 - 20 | 25 - 19 | 1 - 18 | 2 - 17 | 3 - 16 | 4 - 15 | 5 - 14 | 6 - 13 | 7 - 12 | 8 - 11 | 9 - 10 |
| 21 | 22 - 20 | 23 - 19 | 24 - 18 | 25 - 17 | 1 - 16 | 2 - 15 | 3 - 14 | 4 - 13 | 5 - 12 | 6 - 11 | 7 - 10 | 8 - 9 |
| 20 | 21 - 19 | 22 - 18 | 23 - 17 | 24 - 16 | 25 - 15 | 1 - 14 | 2 - 13 | 3 - 12 | 4 - 11 | 5 - 10 | 6 - 9 | 7 - 8 |
| 19 | 20 - 18 | 21 - 17 | 22 - 16 | 23 - 15 | 24 - 14 | 25 - 13 | 1 - 12 | 2 - 11 | 3 - 10 | 4 - 9 | 5 - 8 | 6 - 7 |
| 18 | 19 - 17 | 20 - 16 | 21 - 15 | 22 - 14 | 23 - 13 | 24 - 12 | 25 - 11 | 1 - 10 | 2 - 9 | 3 - 8 | 4 - 7 | 5 - 6 |
| 17 | 18 - 16 | 19 - 15 | 20 - 14 | 21 - 13 | 22 - 12 | 23 - 11 | 24 - 10 | 25 - 9 | 1 - 8 | 2 - 7 | 3 - 6 | 4 - 5 |
| 16 | 17 - 15 | 18 - 14 | 19 - 13 | 20 - 12 | 21 - 11 | 22 - 10 | 23 - 9 | 24 - 8 | 25 - 7 | 1 - 6 | 2 - 5 | 3 - 4 |
| 15 | 16 - 14 | 17 - 13 | 18 - 12 | 19 - 11 | 20 - 10 | 21 - 9 | 22 - 8 | 23 - 7 | 24 - 6 | 25 - 5 | 1 - 4 | 2 - 3 |
| 14 | 15 - 13 | 16 - 12 | 17 - 11 | 18 - 10 | 19 - 9 | 20 - 8 | 21 - 7 | 22 - 6 | 23 - 5 | 24 - 4 | 25 - 3 | 1 - 2 |
| 13 | 14 - 12 | 15 - 11 | 16 - 10 | 17 - 9 | 18 - 8 | 19 - 7 | 20 - 6 | 21 - 5 | 22 - 4 | 23 - 3 | 24 - 2 | 25 - 1 |
| 12 | 13 - 11 | 14 - 10 | 15 - 9 | 16 - 8 | 17 - 7 | 18 - 6 | 19 - 5 | 20 - 4 | 21 - 3 | 22 - 2 | 23 - 1 | 24 - 25 |
| 11 | 12 - 10 | 13 - 9 | 14 - 8 | 15 - 7 | 16 - 6 | 17 - 5 | 18 - 4 | 19 - 3 | 20 - 2 | 21 - 1 | 22 - 25 | 23 - 24 |
| 10 | 11 - 9 | 12 - 8 | 13 - 7 | 14 - 6 | 15 - 5 | 16 - 4 | 17 - 3 | 18 - 2 | 19 - 1 | 20 - 25 | 21 - 24 | 22 - 23 |
| 9 | 10 - 8 | 11 - 7 | 12 - 6 | 13 - 5 | 14 - 4 | 15 - 3 | 16 - 2 | 17 - 1 | 18 - 25 | 19 - 24 | 20 - 23 | 21 - 22 |
| 8 | 9 - 7 | 10 - 6 | 11 - 5 | 12 - 4 | 13 - 3 | 14 - 2 | 15 - 1 | 16 - 25 | 17 - 24 | 18 - 23 | 19 - 22 | 20 - 21 |
| 7 | 8 - 6 | 9 - 5 | 10 - 4 | 11 - 3 | 12 - 2 | 13 - 1 | 14 - 25 | 15 - 24 | 16 - 23 | 17 - 22 | 18 - 21 | 19 - 20 |
| 6 | 7 - 5 | 8 - 4 | 9 - 3 | 10 - 2 | 11 - 1 | 12 - 25 | 13 - 24 | 14 - 23 | 15 - 22 | 16 - 21 | 17 - 20 | 18 - 19 |
| 5 | 6 - 4 | 7 - 3 | 8 - 2 | 9 - 1 | 10 - 25 | 11 - 24 | 12 - 23 | 13 - 22 | 14 - 21 | 15 - 20 | 16 - 19 | 17 - 18 |
| 4 | 5 - 3 | 6 - 2 | 7 - 1 | 8 - 25 | 9 - 24 | 10 - 23 | 11 - 22 | 12 - 21 | 13 - 20 | 14 - 19 | 15 - 18 | 16 - 17 |
| 3 | 4 - 2 | 5 - 1 | 6 - 25 | 7 - 24 | 8 - 23 | 9 - 22 | 10 - 21 | 11 - 20 | 12 - 19 | 13 - 18 | 14 - 17 | 15 - 16 |
| 2 | 3 - 1 | 4 - 25 | 5 - 24 | 6 - 23 | 7 - 22 | 8 - 21 | 9 - 20 | 10 - 19 | 11 - 18 | 12 - 17 | 13 - 16 | 14 - 15 |
| 1 | 2 - 25 | 3 - 24 | 4 - 23 | 5 - 22 | 6 - 21 | 7 - 20 | 8 - 19 | 9 - 18 | 10 - 17 | 11 - 16 | 12 - 15 | 13 - 14 |
December 14th, 2023 at 5:37:35 PM
permalink
Quote: ThatDonGuyQuote: DRichQuote: WizardIn tennis, players switch sides after every odd-numbered game. So, that was not the best example of a home-side advantage.
I thought in tennis they switched sides after every sixth game.
link to original post
No - change sides every other game (or, in a tiebreak, after every six points), starting with the second game of the match.
Usually, balls are changed after the first seven games, and then every nine games after that.
link to original post
Thank you, I must have been thinking of the tie breaker.
At my age, a "Life In Prison" sentence is not much of a deterrent.
December 14th, 2023 at 6:48:38 PM
permalink
Quote: unJonI don’t understand the question. 25 players. 6 shuffleboard courts? 2 people or 4 people (in 2 teams of 2) play at once? And you just need everyone to play everyone else (and with everyone else if teams)?
link to original post
With 25 players, every individual player will play 24 games. There are six courts, each with two sides, for a total of 12 sides. It is desired that each player play each of the 12 sides twice.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 15th, 2023 at 11:18:59 AM
permalink
Quote: WizardQuote: unJonI don’t understand the question. 25 players. 6 shuffleboard courts? 2 people or 4 people (in 2 teams of 2) play at once? And you just need everyone to play everyone else (and with everyone else if teams)?
link to original post
With 25 players, every individual player will play 24 games. There are six courts, each with two sides, for a total of 12 sides. It is desired that each player play each of the 12 sides twice.
link to original post
Doesn't my table do that?
Notice that each of the numbers from 1 to 25 appears twice in each of the 12 columns - once to the left of the dashes, and once to the right. If each column is a court/side (which it is - "A1" is side 1 of court A, and "C2" is side 2 of court C), then each player is on each court exactly twice.
