I was able to reproduce this number.
I wrote a Javascript program to produce a file of all 35,690 combos.
I used a linux sort unique command to filter out dupes and came up with 4,285 UNIQUE combos.
Then, I reset the program to NOT use both of the 9,L8,L7,5 tiles since the are the same in value. E.g. the 4-5 tile is the same as the 3-6 tile so, I removed one of the tiles.
This produced 20,474 total combinations and 3,755 UNIQUE combinations of hands. Still not the 3,620 I read about.
Dr. Allen in his book, "How to play Pai Gow", claims there are 8,130 combinations.
Question is: How are we defining UNIQUE HANDS?
Question 2: How did you get 3,620 UNIQUE hands?
Thanks for your time and help.
One way to look at it is this:Quote: DougDI read there are 35,690 total combinations of 32 tiles taken 4 at a time.
I was able to reproduce this number.
I wrote a Javascript program to produce a file of all 35,690 combos.
I used a linux sort unique command to filter out dupes and came up with 4,285 UNIQUE combos.
Then, I reset the program to NOT use both of the 9,L8,L7,5 tiles since the are the same in value. E.g. the 4-5 tile is the same as the 3-6 tile so, I removed one of the tiles.
This produced 20,474 total combinations and 3,755 UNIQUE combinations of hands. Still not the 3,620 I read about.
Dr. Allen in his book, "How to play Pai Gow", claims there are 8,130 combinations.
Question is: How are we defining UNIQUE HANDS?
Question 2: How did you get 3,620 UNIQUE hands?
Thanks for your time and help.
link to original post
There are 16 distinct tiles, in terms of value, in a pai gow set. So, in hands with 4 tiles,
There are 120 two pair hands
there are 16 single-pair hands, each with a 15 COMB 2 set of unique tiles =16 x 105 = 1680
unique hands with no pairs are 16 COMB 4 = 1820
TOTAL 3620
I'm a dummy.
Those two tiles are the same...chop gow.Quote: TigerWuThe 4-5 tile and the 3-6 tile are NOT the same.... They both total 9, but the 4-5 tile outranks 3-6 tile, so a hand with the former would win against a hand with the latter, all other things being equal.
link to original post
Click on picture for larger version.
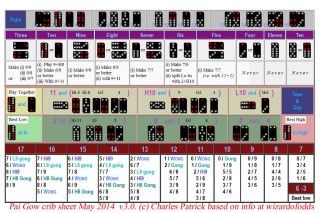
If in a house game, rather than the casino version, the tiles are worth different values, then you may be correct that there are more unique hands. When I worked out the strategy I just assumed there were 16 different tile values with two of each.
Quote: TigerWuthe 4-5 tile outranks 3-6 tile,
link to original post
This is not true. What is your source?
Lots of dust on that book!
I modified my script to treat the 2 Gee tiles as a chop pair. That worked. 3,620 on the nose.
I have to think more why the the 2 gee tiles are considered a chop bo while they have different individual ranks.
Thanks for your immediate response.
Quote: WizardQuote: TigerWuthe 4-5 tile outranks 3-6 tile,
link to original post
This is not true. What is your source?
link to original post
Quote: UP84Those two tiles are the same...chop gow.Quote: TigerWuThe 4-5 tile and the 3-6 tile are NOT the same.... They both total 9, but the 4-5 tile outranks 3-6 tile, so a hand with the former would win against a hand with the latter, all other things being equal.
link to original post
link to original post
LOL..... I saw "3-6" and my brain read it as a Gee Joon tile.
BUT, when I thought more about it the G3 and G6 are the same even with their different ranks.
The reason for this is you only split G3,G6 when when 3rd and 4th tiles are 6-4, 6-5, non-pair 6-6 --->hands of 0,1,2.
You make:
7-9
8-9
9-9
In this case it doesn't matter which hand you place the G3 and G6. The high tile will be selected from the 3rd and 4th tile. Any of these will always be higher in rank than G3 or G6.
It seems as though G3 and G6 are the same even if they have different ranks.
In the end you can say they are "distinct without a difference".
The stated 3,620 UNIQUE combinations wins the day!
Quote: DougDI've never seen different rankings for G6 and G3. They "rank" 15th and 17th. respectively.
This guide for an Australian casino ranks both Gee Joon tiles last in 16th place. That's just an example... I know I've seen other sources rank them that way, but it's not common.
EDIT: Here are a couple more casinos, one in California, one in London, that also rank Gee Joon tiles together in 16th place:
Star's Casino
London Clubs International
Yes, there are some jurisdictions that have the 5 ranked as 16, with the Gee Joon ranked as 15 when it’s played as 6, and the Gee Joon ranked as 17 when it’s played as 3.Quote: TigerWuQuote: DougDI've never seen different rankings for G6 and G3. They "rank" 15th and 17th. respectively.
This guide for an Australian casino ranks both Gee Joon tiles last in 16th place. That's just an example... I know I've seen other sources rank them that way, but it's not common.
EDIT: Here are a couple more casinos, one in California, one in London, that also rank Gee Joon tiles together in 16th place:
Star's Casino
London Clubs International
link to original post
However, the dual ranking for the Gee Joon is in reality irrelevant because whenever the Gee is counted as 6 (rank 15), it's NEVER the determining tile in hands of equal value. Alternatively, if the Gee is played with the 5 (which is truly the only relevant scenario for the GJ 15/17 ranking rule) it's ALWAYS counted as a 3, and the only scenario where this would come into play is where the other hand is a Gee + 5…in which case there would be a copy which would go to the Banker via the copy rule.
ranked the lowest."
Not very common.
Very strange.
I think this is do to the splitting that I explained in a previous post.
Again, a "distinction without a difference". Rank them individually as last or 15th and 17th and it won't make a difference in the game or strategy.
Quote: UP84Yes, there are some jurisdictions that have the 5 ranked as 16, with the Gee Joon ranked as 15 when it’s played as 6, and the Gee Joon ranked as 17 when it’s played as 3.
However, the dual ranking for the Gee Joon is in reality irrelevant because whenever the Gee is counted as 6 (rank 15), it's NEVER the determining tile in hands of equal value. Alternatively, if the Gee is played with the 5 (which is truly the only relevant scenario for the GJ 15/17 ranking rule) it's ALWAYS counted as a 3, and the only scenario where this would come into play is where the other hand is a Gee + 5…in which case there would be a copy which would go to the Banker via the copy rule.
link to original post
Good post. I was going to post as such, but you beat me to it.
Been using the Pai Gow Calculator.
I put in a hand of teen,day,H8,5
It gave me a best "Return" of .58
Using the following info:
W=13,836
P = 5,388
L=1,251
the closest I could get is: ((W*.95) + P)/35960 = .51
What is the right way to calculate "Return"
What is meant by "return"
Why not use "hand expectation"?
Thanks
What did you use for the four game setting parameters on the Pai Gow Calculator?Quote: DougD… I put in a hand of teen,day,H8,5 …
That's it
Teen (12), Day(2),H8,5
click analyze.........
Standards I left alone.
For 1 wagered a 0.580864 profit/loss (return). “Return” is a better fit for the column heading.
You should be using Win*.95 less Lose which in your case is (13836*.95-1251)/20475 = 0.58...Quote: DougDWizard,
Been using the Pai Gow Calculator.
I put in a hand of teen,day,H8,5
It gave me a best "Return" of .58
Using the following info:
W=13,836
P = 5,388
L=1,251
the closest I could get is: ((W*.95) + P)/35960 = .51
What is the right way to calculate "Return"
What is meant by "return"
Why not use "hand expectation"?
Thanks
link to original post
Personally I have different numbers (13612,5612,1251), but then I use a different House Way for my calculations (probably based on what I saw in London).
The P doesn't really factor into the analysis. You have to subtract the L (or define it as a negative) and divide by 20,475, not 35,960.Quote: DougDWizard,
Been using the Pai Gow Calculator.
I put in a hand of teen,day,H8,5
It gave me a best "Return" of .58
Using the following info:
W=13,836
P = 5,388
L=1,251
the closest I could get is: ((W*.95) + P)/35960 = .51
What is the right way to calculate "Return"
What is meant by "return"
Why not use "hand expectation"?
Thanks
link to original post
Here's a little more difficult question:
Why are the number of hands always 20,475 (W+L+P)
I'm working on a VB program that plays the 3620 (dealer) unique hands against the 35,960 possible hands (player).
When I have a hand where there isn't enough tiles to play the hand, I skip that hand from the 35,960 hands.
For example: one hand (dealer) has teen,teen,day,day. That hand can't be played against a player hand that would contain one of these tiles b/c there are none of these tiles left to receive.
When I hit a hand like that I do get the 20,475 hands played. -Great!
However, when there are enough of tiles for both hands I get 26,650 hands that were played not the 20,475 when tiles are used up and the hand is skipped.
Do you know why the 20,475 seems to be a constant?????
Not a easy question but perhaps you may know the answer. I hope so. It's driving me nuts!!!!
I'm playing much more hands against the player when there are enough tiles for both hands !!!???
Personally you have a similar situation to (single deck) BJ hands and the chances of the next card(s). There were 4 Aces, 4 Twos ... 4 Nines, 16 Tens at the start. Once you have 6,5 vs Dealer's 5, there are 2 Fives and 3 Sixes left. (With multiple decks you might start with, say, 24/96 of each.)
As charliepatrick noted, although there are 35,960 combinations of 4 tiles available to the Player (Combin(32,4)), in order to get the total playable scenarios, one must look at the number of 4 tile combinations available to the DEALER from the remaining 28 tiles...Combin(28,4) = 20,475Quote: DougDThanks again for your last response.
Here's a little more difficult question:
Why are the number of hands always 20,475 (W+L+P)
I'm working on a VB program that plays the 3620 (dealer) unique hands against the 35,960 possible hands (player).
When I have a hand where there isn't enough tiles to play the hand, I skip that hand from the 35,960 hands.
For example: one hand (dealer) has teen,teen,day,day. That hand can't be played against a player hand that would contain one of these tiles b/c there are none of these tiles left to receive.
When I hit a hand like that I do get the 20,475 hands played. -Great!
However, when there are enough of tiles for both hands I get 26,650 hands that were played not the 20,475 when tiles are used up and the hand is skipped.
Do you know why the 20,475 seems to be a constant?????
Not a easy question but perhaps you may know the answer. I hope so. It's driving me nuts!!!!
I'm playing much more hands against the player when there are enough tiles for both hands !!!???
link to original post
I agree that there are Combin(28,4) = 20,475 but i think that assumes that the dealer can't have any of the tiles in the player hand. This is consistent with my above post when the dealer has, for example, teen,teen, Gee Gee there are 20475 hands left for the dealer to play against the player. But, what happens when the dealer has teen,teen, and two other tiles that are not the same.
In this case I get the dealer can play against 26,650 player combos. When the dealer has any 4 tiles that are not the same, there are 34,226 combos.
For example:
When the dealer has TEEN, TEEN, GEE,GEE, I get W=20475, L=0, P=0. Total of 20475 played against the player. This is consistent with Combin(28,4) = 20,475
However, when the dealer has TEEN,TEEN H7, H6, I get W=13007,L=28, P=13615. Total of 26650 hands played against the player.
When the dealer has TEEN,H7,L6,9 (all unique tiles) I get W=20066, L=3623, P=10537. Total of 34226 played against the player.
Does this make any sense???????
THANKS.......
I think using 20475 combinations for all hands would make the Pia Gow calculator give results that may not be correct. Not sure.
I would like to straighten out the # of combinations question first. Whats your thoughts on the # combinations for dealer v. player as stated in my last post. Without the proper # of combinations for Dealer v player, all the rest is moot!!!!!!!
What's your thoughts re: # combinations. I don't think it's the 20475 for all dealer v. player.
Thanks for noticing my problem with w/l/p. That's a complicated algorithm that I will take another look at.
Thanks.
I think you mean 28*27*26*25/4*3*2*1.
Yes, that comes to 20475 b/c " four of these are used by one side".
What happens when they are not used up by one side" ?????
Therefore, all the hands can't always have on side using then up.
But, it looks like the calculator always uses 20475.
When one side or the other has 2 hands with 2 same tiles out on the hand the number of dealer v. player is 20,475
ex: teen,teen,day,day
......................................................................2 same tiles out on one hand ............................................... 26,650
ex: teen, teen, any not same, any not same
......................................................................4 tile out on both hands that are not the same..........................34.226
ex:
any not same, any not same,any not same, any not same
The 20,475 constant used by the calculator appears to be a little strange.
What do you think????
THANKS !!!!
That would figure when either side uses up 2 sets of tiles. Ex: teen,teen,day,day. comb(28,4)
But here are other situations where this is not the case.
I calculated the following by writing a quick program:
When one side or the other has 2 hands with 2 same tiles out on the hand the number of dealer v. player is 20,475
ex: teen,teen,day,day
......................................................................2 same tiles out on one hand ............................................... 26,650
ex: teen, teen, any not same, any not same
......................................................................4 tile out on both hands that are not the same..........................34,226
ex:
any not same, any not same,any not same, any not same
The 20,475 constant used by the calculator appears to be a little strange.
What do you think????
THANKS !!!!
It's really quite straightforward. The number of possible hands is equal to number of 4 tile combinations that can be drawn without replacement from a set of 28 tiles (the number of tiles that remain available to the dealer after any 4 tiles have been dealt to the player). The formula is n! / ((n-r)!r!.Quote: DougDI'm trying to figure out why the Pai Gow Calculator always uses 20,475 for the number of dealer v. player hands.
That would figure when either side uses up 2 sets of tiles. Ex: teen,teen,day,day. comb(28,4)
But here are other situations where this is not the case.
I calculated the following by writing a quick program:
When one side or the other has 2 hands with 2 same tiles out on the hand the number of dealer v. player is 20,475
ex: teen,teen,day,day
......................................................................2 same tiles out on one hand ............................................... 26,650
ex: teen, teen, any not same, any not same
......................................................................4 tile out on both hands that are not the same..........................34,226
ex:
any not same, any not same,any not same, any not same
The 20,475 constant used by the calculator appears to be a little strange.
What do you think????
THANKS !!!!
link to original post
With n=28 and r=4, the number works out to be 20,475.
Sorry to say but I think you have a bug in your program (or spreadsheet logic). For instance, 26650 is 650x41, as 41 is prime and more than the number of tiles, it shouldn't be a factor of the ways to make the player's hand. So you must be double counting hands somewhere.Quote: DougD...The 20,475 constant used by the calculator appears to be a little strange. What do you think????
Many of us have explained why the answer should be 20475: once four tiles have been drawn, regardless of what they are, there are 28 left. There are then 20475 ways to pick four tiles from 28.
When one side removes 2 tiles of one rank and two tiles of another rank there are 20475 combos left. Makes lots of sense. But that's not the only situation as shown in my previous post.
So, if you remove only one tile of each rank you still have only 20,475 combinations remaining? Makes little sense to me.
I have a short VB program that will show what I previously posted. Any way to get it to you.
What you are saying is true but that's not in reality what is happening when other combinations are removed. It's not ALWAYS there are no tiles left for the other side. Just simple logic........ Think about it......
Thanks for the response. I appreciate it.
No. If there are 4 different tiles out that are not the same, the remaining 4-tile combinations is still 20,475.Quote: DougD4 tile out on both hands that are not the same...34,226
link to original post
You need to look more closely at the data your program is generating.
For example, say the First Hand is Gee, 5, 9 and 11 (four different tiles).
If in this scenario your program is producing 34,226 Second Hands, then I guarantee that within the set of those 34,226 program-generated Second Hands (1) there are impossible pair scenarios (ie the Second Hand cannot have a Gee,5,9 or 11 pair), and/or (2) there are more then the number of possible scenarios for any given tile combo (staying with the Gee, 5, 9, 11 First Hand example, in Second Hands that have a 5 and where the other 3 tiles are, say, Teen, H10, L8, there are only 8 possible 5, Teen, H10, L8 combinations.
Yes, I am playing against more hands than i should be. I see what you are saying and have to screen out more hands.
THANKS.
I read a dealer hand, let's say, 4,5,6,7. I subtract 1 for each of those tiles from the tiles in the array.
This would give me 1 tile left to use for the 4,5,6,7 tiles.
Then I read a player hand,say, 4,5,6,7 from the 35,690 possible hands and subtract 1 from the tiles array for each of those tiles.
That leaves 0 tiles left for the 4,5,6,7 tiles --- and the hand is possible to play. When a tile in the array goes negative, that hand can't be used. For example: (same dealer hand 4,5,6,7)
Let's say the next player hand has tiles of 4,4,10,11
In this case we used 1 of the" 4" tiles for the dealer and trying to use 2 more of the "4' tiles for the player hand.
Now, Tile(4) in the array is -1 and the hand cannot be used. Then go back and get another player hand........
Any time tiles in the array goes negative the hand CANNOT be used.
Very simple logic but NOT working. Hmmmmm........?????? Got me stumped......
Can't help you any further as I don't know squat about this kind of programming. I just know the math (or maths as they would say in the UK).Quote: DougDAll I do to determine a usable hand if very simple (but obviously not working) is that I have an array of 16 tiles initialized at 2 tiles each called tiles(). The dealer and player tiles and tile array are based on the tile ranks 1-16.
I read a dealer hand, let's say, 4,5,6,7. I subtract 1 for each of those tiles from the tiles in the array.
This would give me 1 tile left to use for the 4,5,6,7 tiles.
Then I read a player hand,say, 4,5,6,7 from the 35,690 possible hands and subtract 1 from the tiles array for each of those tiles.
That leaves 0 tiles left for the 4,5,6,7 tiles --- and the hand is possible to play. When a tile in the array goes negative, that hand can't be used. For example: (same dealer hand 4,5,6,7)
Let's say the next player hand has tiles of 4,4,10,11
In this case we used 1 of the" 4" tiles for the dealer and trying to use 2 more of the "4' tiles for the player hand.
Now, Tile(4) in the array is -1 and the hand cannot be used. Then go back and get another player hand........
Any time a tile in the array goes negative the hand CANNOT be used.
Very simple logic but NOT working. Hmmmmm........?????? Got me stumped......
link to original post


