compound payout, single bet

Hi all,

Seeking some advice on how to calculate the following please:

the return to player if a single $5 bet is placed on a betting zone that pays out if 3 aces in a row are drawn. the tricky part for me is, the same $5 bet stays live (in play) and pays out for the first and second aces (if drawn).

i thought of dividing the $5 bet into 3 and making that the cost to play, but that doesn't work, any ideas?

hope the question makes sense

Sounds similar to the "Grand Slam" bet where the player gets paid depending how often something keeps on happening. Basically the stick man has to keep count (or they add a table screen) showing how many runs the shooter has scored. The bet is then resolved when either the maximum is reached of the run ends. Also reference some of the Craps bets where tokens on the layout show which numbers have been rolled.
https://wizardofodds.com/games/craps/side-bets/bonus-craps/
https://wizardofvegas.com/forum/gambling/other-games/29230-diceball/

Hi charliepatrick, thank you for the reply, the links aren't exactly what I'm after, thought your summary is accurate. The player gets paid for 1 ace, then 2 if it follows and then 3 (the maximum) if that follows the second ace; but in this scenario only has to place the initial bet, which remains until the maximum 3 aces in a row come out or an ace does not come out. Basically I'd like to know how to do the maths on something like this

Quote: joanmiller

Hi charliepatrick, thank you for the reply, the links aren't exactly what I'm after, thought your summary is accurate. The player gets paid for 1 ace, then 2 if it follows and then 3 (the maximum) if that follows the second ace; but in this scenario only has to place the initial bet, which remains until the maximum 3 aces in a row come out or an ace does not come out. Basically I'd like to know how to do the maths on something like this
link to original post

If you would kindly lay out the entire payouts and how the deal is dealt, we can show you how to to calculate.

The simplest way is to consider each step as the next three cards are dealt. At the end you have one of four outcomes.
(i) The first card isn't an Ace - Lose,
(ii) The first card is an Ace, the second one isn't - Pay out the "One Ace" prize,
(iii) The first card is an Ace, the second card is an Ace, the third one isn't - Pay out the "Two Aces" prize,
(iv) All three cards are Aces - Pay out the "Three Aces" prize.
For each outcome, multiply their probabilities by their Payouts (include losses in this); add them all up and you have the House Edge.

For a single deck it might be
(i) Chance = 12/13.
(ii) 1/13 times 48/51
(iii) 1/13 times 3/51 times 48/50
(iv) 1/3 times 3/51 times 2/50.

Interestingly 10/1 25/1 and exactly 500/1 would represent a fair bet!

thank you charliepatrick and also unJon, im sorry for my inability to get this but i still get stuck with the cost to play and rtp.

as you have said above the steps are either no, 1, 2 or 3 aces after the bet is placed. the bet is placed and remains until either a no ace or 3 aces condition is met

i have a table but can't attach a screen shot but basically i know the probabillity and the odds of each ace but how do i fill in the column (in excel) regarding the cost to play at each step, if only one bet is placed?

perhaps each cost to play is not relevant? i should just take the average return to player across all the 1,2,3 ace outcomes?

Quote: charliepatrick

The simplest way is to consider each step as the next three cards are dealt. At the end you have one of four outcomes.
(i) The first card isn't an Ace - Lose,
(ii) The first card is an Ace, the second one isn't - Pay out the "One Ace" prize,
(iii) The first card is an Ace, the second card is an Ace, the third one isn't - Pay out the "Two Aces" prize,
(iv) All three cards are Aces - Pay out the "Three Aces" prize.
For each outcome, multiply their probabilities by their Payouts (include losses in this); add them all up and you have the House Edge.

For a single deck it might be
(i) Chance = 12/13.
(ii) 1/13 times 48/51
(iii) 1/13 times 3/51 times 48/50
(iv) 1/3 times 3/51 times 2/50.

Interestingly 10/1 25/1 and exactly 500/1 would represent a fair bet!
link to original post

charliepatrick,

I have one slight correction to your otherwise excellent response.

joanmiller, the OP, stated that the player gets paid as each ace appears, so your last two steps should be

(iii) The first card is an Ace, the second card is an Ace, the third one isn't - Pay out the "One Ace" and "Two Aces" prizes,
(iv) All three cards are Aces - Pay out the "One Ace", "Two Aces", and "Three Aces" prizes.

Hope this helps!

Dog Hand

Quote: DogHand

....charliepatrick,

I have one slight correction to your otherwise excellent response.

joanmiller, the OP, stated that the player gets paid as each ace appears...

Thanks for your kinds words.

The references I gave earlier, showing how similar bets are handled by land-based casinos, suggest a better way of handling the bet might be to keep track of its status until the bet is finished. Otherwise one could always turn it into a "Place" bet on an Ace appearing before a "non-Ace", (paying say 11.5 to 1) but that wouldn't pay a jackpot for three in a row, so not what the OP wants.

However, taking on your suggestion, let's assume that it's a nice new side-bet for Casino War (ignore the drawings from ties). Then suppose your first card is an Ace, and the base game needs to continue and move on. The OP wants to pay out (in my example 10 to 1) but the casino needs to keep track that the wager won, for the next base game. So if there's now a second Ace, the casino needs to pay out 15 to 1 (total 25 to 1), if it's not an Ace return the wager (or remove the lammer). After the second Ace, similarly remember that as well (say put a second lammer on top). etc. Yes it's possible, but in practice it's easier to pay out the total winnings once. (btw If this way was chosen I would adjust the odds to pay 10/1, then an additional 25/1, then an additional 225/1, or 100/1 if one wanted a House Edge.)

Mathematically it doesn't matter when you pay out the winnings, but you do need to remember to return the original wager (or pay out X+1) if you win the first/second part but then lose.


Thus you can work on the assumption that in total you'll pay X, Y and Z (it doesn't matter how it's done in practice). (I haven't looked into it but there are some bets on Roulette which go across two or more spins. I can't remember how these are handled.)


Obviously in an online environment, you can code whatever looks and feels the best. Personally I would move the bet into a box marked (One Ace achieved) with a kitty "winnings so far" showing £10 and so on. When the bet is resolved then you pay it out.

Quote: joanmiller

thank you charliepatrick and also unJon, im sorry for my inability to get this but i still get stuck with the cost to play and rtp.

as you have said above the steps are either no, 1, 2 or 3 aces after the bet is placed. the bet is placed and remains until either a no ace or 3 aces condition is met

i have a table but can't attach a screen shot but basically i know the probabillity and the odds of each ace but how do i fill in the column (in excel) regarding the cost to play at each step, if only one bet is placed?

perhaps each cost to play is not relevant? i should just take the average return to player across all the 1,2,3 ace outcomes?
link to original post

Hi joanmiller, here is my suggestion for a solution in Excel. I provide the formulas and the values as screen shots and hope you will be able to reproduce it.





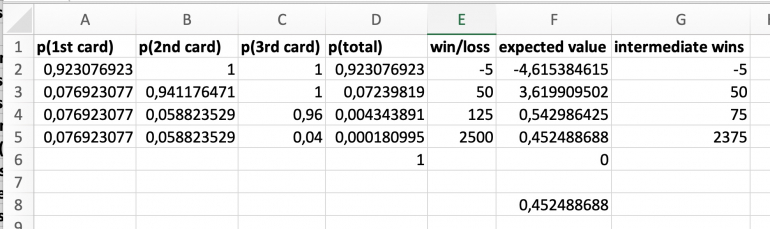
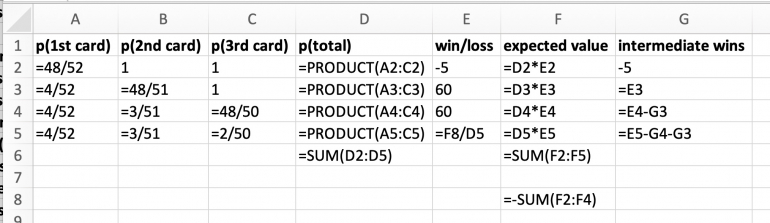
Columns A through C have the single probabilities which then are multiplied in column D. Cell D6 has the plausibility check that all probabilities add up to 1.
The probabilities in rows 2 through 5 correspond to charliepatrick's solutions (i) through (iv).

Column E takes the wins and losses, here based on a $5 bet. The big win is calculated from the other two wins assuming a fair game, indicated by ev=0 in cell F6.
I preloaded it with charliepatrick's solution but you may play around with different combinations of winnings, e.g. 60-60-60, 5-500-11500, and many others.
Remark: Cell F8 is an intermediate sum to avoid circular referencing in Excel.




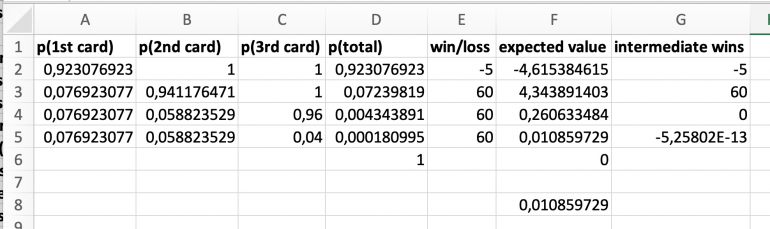
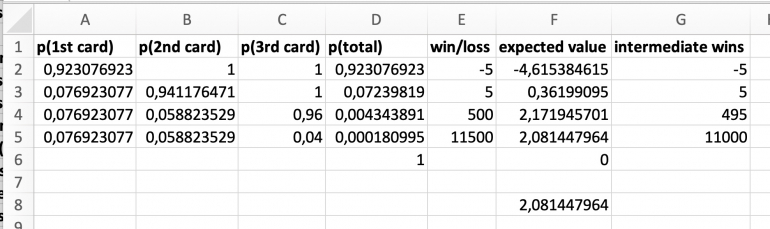
The expected value calculated in column F is valid only for the case in which a non-ace ends the sequence.

If aces are paid as soon as they appear, while keeping the initial bet working, the subsequent winnings have to be reduced by the previous winnings already paid, see column G.
A funny thing happens if the three winning amounts are 60-60-60. Only the first 60 will be paid but nothing else will be payed on further aces. Nevertheless it is correct, because any of the combinations, 1 ace, 2 aces, 3 aces, will each pay $60 to the initial $5 and waiting for further aces is unnecessary.

Hi Thomas K,

Thank you so much for the reply, can you please show me how to do a screen shot like that so i can show you my excel tables (and what i must have done wrong). Also thank you to everyone else for replying and your help and patience with my lack of understanding.

thank you so much for your reply here, the process of keeping track of the stage/level the bet is on is ok (like how many aces in a row are attributable to that initial bet) and when the payout is made is not so important although, your suggestion is a great one i think. it's just about the maths behind the bet/payout at each stage, like you have said the timing of the payout doesn't change the math. if i figure out how to show a screenshot i can show the requirements and be more clear but not able to drag an image into the post so not too sure at the moment

Quote: joanmiller

thank you so much for your reply here, the process of keeping track of the stage/level the bet is on is ok (like how many aces in a row are attributable to that initial bet) and when the payout is made is not so important although, your suggestion is a great one i think. it's just about the maths behind the bet/payout at each stage, like you have said the timing of the payout doesn't change the math. if i figure out how to show a screenshot i can show the requirements and be more clear but not able to drag an image into the post so not too sure at the moment
link to original post

There is an "insert my picture" button just below the post/preview/cancel buttons.

You may need to resize or crop the image before uploading. I generally find 800x800 a useful size.

Quote: joanmiller

thank you so much for your reply here, the process of keeping track of the stage/level the bet is on is ok (like how many aces in a row are attributable to that initial bet) and when the payout is made is not so important although, your suggestion is a great one i think. it's just about the maths behind the bet/payout at each stage, like you have said the timing of the payout doesn't change the math. if i figure out how to show a screenshot i can show the requirements and be more clear but not able to drag an image into the post so not too sure at the moment
link to original post

joanmiller,

If the timing of the payouts is unimportant, then one easy solution is to change the paytable to account for the number of consecutive Aces.

For example, let's say the current paytable pays $25 for the first Ace, $200 for the second, and $1000 for the third. In this case, the total payout for one Ace is $25; for two Aces, $225; and for three Aces, $1225.

Why not simply give the paytable as follows:

# of Aces Pays
1 $25
2 $225
3 $1225

Then wait until the player gets either a non-Ace or three consecutive Aces before resolving the bet. This will avoid having to keep track of the payouts with lammers as the hand progresses.

Dog Hand

Quote: joanmiller

Hi Thomas K,

Thank you so much for the reply, can you please show me how to do a screen shot like that so i can show you my excel tables (and what i must have done wrong). Also thank you to everyone else for replying and your help and patience with my lack of understanding.
link to original post

I completely understand your trouble with screen shots - I also had some issues.

1) First there is the question how to create the screen shot on your local computer. Back when I had a Windows laptop in the office, the company provided us with "Greenshot" which is free, as far as I understand.
I'm now using MAC OS which has Applications/Utilities/Screenshot.app.

2) Once you have the screen shot on your local computer you need to make sure that the file type is suitable for the forum. On MAC OS Screenshot.app by default creates .png files which I found the forum does not accept. I have to convert my pictures to JPEG to be able to upload them. The MAC OS Applications/Preview.app is not only used used to view the picture but it also offers the "Export..." functionality which includes optional conversion of file formats.
Depending on your own setup you might need to find a file converter that works for you.

2a) My tip for file names of the target pictures: The screen shot apps tend to create defualt file names with date and time stamps which might be hard to recognize. Choose file names that let you easily identify your pictures in the "User Image Gallery" under "Insert My Picture" in the forum.

3) Upload your picture to the forum using the "Insert My Picture" button and then the upload button in the User Image Gallery.
The link to the picture will be added to your reply, you currently are editing, at the current curser position and the picture will be kept in the User Image Gallery for future reference. The previews of the images are quite tiny but mouse over will display the file name, which is why these names should be easily identifyable.

thank you so much for trying to help, unfortunately under post/preview/cancel there is nothing except 'check formatting codes' on the right

thank you for the help also doghand, but i really need the formulas in excel so i can update and change things, or even apply the same logic to other outcomes

i wish i could show the excel but basically the columns i have are 1ace, 2 aces, 3 aces and the rows are:
-probability of winning [7.2398, 0.4344, 0.0181]
-odds of winning (1-in) [13.8, 230.2, 5525]
and i need
-cost to play
-payout for winning (the formula)
-return to player

Hi joanmiller, are you sure that this button is missing in your reply view?
I would be surprised if one of the Administrators needed to explicitly assign this function to your account ...

Quote: ThomasK

Hi joanmiller, are you sure that this button is missing in your reply view?
I would be surprised if one of the Administrators needed to explicitly assign this function to your account ...


link to original post

I think it may be one of the spambrakes applied to new accounts.

Joanmiller, keep posting good posts, and the features should become available. I am not aware of a way for administrators to wave a magic wand and turn off the spambrakes.

Quote: joanmiller

thank you so much for trying to help, unfortunately under post/preview/cancel there is nothing except 'check formatting codes' on the right

thank you for the help also doghand, but i really need the formulas in excel so i can update and change things, or even apply the same logic to other outcomes

i wish i could show the excel but basically the columns i have are 1ace, 2 aces, 3 aces and the rows are:
-probability of winning [7.2398, 0.4344, 0.0181]
-odds of winning (1-in) [13.8, 230.2, 5525]
and i need
-cost to play
-payout for winning (the formula)
-return to player
link to original post

I guess, your screen shot would be helpful to better understand what you are looking for.
About your additional information:

Quote: joanmiller

-probability of winning [7.2398, 0.4344, 0.0181]

These value seem to be percentages and you will find them in my screen copy in column D
row 3 - 0.072398 = 7.2398%
row 4 - 0.004344 = 0.4344%
row 5 - 0.000181 = 0.0181%
These values are the products of the probabilities of colimns A, B, and C.
Please klick the spoiler button for the Excel formulas behind the values.

Quote: joanmiller

-odds of winning (1-in) [13.8, 230.2, 5525]

These three are the inverse of the probabilities given above:
1 / 7.2398% = 13.8
1 / 0.4344% = 230.2
1 / 0.0181% = 5525

Quote: joanmiller

-cost to play

My understanding is that cost to play is $5 because you said that you wager $5 and let it ride as long as aces are dealt.
I might be completely wrong if "cost to play" has a very different definition.

Quote: joanmiller

-payout for winning (the formula)
-return to player

I will try to answer this after having seen your Excel.

Quote: Dieter

Quote: ThomasK

Hi joanmiller, are you sure that this button is missing in your reply view?
I would be surprised if one of the Administrators needed to explicitly assign this function to your account ...


link to original post

I think it may be one of the spambrakes applied to new accounts.

Joanmiller, keep posting good posts, and the features should become available. I am not aware of a way for administrators to wave a magic wand and turn off the spambrakes.
link to original post

Thanks for your clarification.

Do I understand it right, that one has to, kind of, "earn" the right to post pictures by posting an initial number of good posts?
Would you be able to give the number of posts needed until this feature is activated?

Quote: joanmiller

thank you so much for trying to help, unfortunately under post/preview/cancel there is nothing except 'check formatting codes' on the right

thank you for the help also doghand, but i really need the formulas in excel so i can update and change things, or even apply the same logic to other outcomes

i wish i could show the excel but basically the columns i have are 1ace, 2 aces, 3 aces and the rows are:
-probability of winning [7.2398, 0.4344, 0.0181]
-odds of winning (1-in) [13.8, 230.2, 5525]
and i need
-cost to play
-payout for winning (the formula)
-return to player
link to original post

I have an idea for a workaround! Please try the following:
1) Go to your Excel sheet.
2) Show the formulas. Please see this video which might help you switching the view.
3) Mark the region holding the formulas and values of your sheet.
4) Copy that region (e.g. CTRL-C).
5) Paste (e.g. CTRL-V) that into your reply. Do not edit this portion of your reply. The contents of the cells will be separated by vertical tabs and I should be able to insert this text back into my own Excel.

Quote: ThomasK

Quote: Dieter

Quote: ThomasK

Hi joanmiller, are you sure that this button is missing in your reply view?
I would be surprised if one of the Administrators needed to explicitly assign this function to your account ...


link to original post

I think it may be one of the spambrakes applied to new accounts.

Joanmiller, keep posting good posts, and the features should become available. I am not aware of a way for administrators to wave a magic wand and turn off the spambrakes.
link to original post

Thanks for your clarification.

Do I understand it right, that one has to, kind of, "earn" the right to post pictures by posting an initial number of good posts?
Would you be able to give the number of posts needed until this feature is activated?
link to original post

It has been so long since I had a new account, I honestly do not know. Image hosting was added well after my probationary period was up.

I know that posting links is restricted for new members. I thought that images were allowed, but maybe not.

I don't know what the magic formula is for determining how many days and posts and whatnot are needed to disable the restrictions.

Thank you so much to everyone for trying to help, I really appreciate it a lot. I'll try to explain without the screenshot and hopefully I make sense.

My biggest problem is that I don't know how to apply the cost of the bet to the calculation of the return to player and therefore can't figure out the house edge.

you are right the bet is $5 but because it stays in play (without any additional player contribution) until either a 'no ace' case or a '3 aces' case i dont actually know what the cost to play is. i mean it costs $5 but the potential for multiple payouts on the initial bet are making it hard for me to understand how to calculate the house edge, and while i thank every one for the help it's really the theory and maths that i need, because if it was for 4 aces or 2 kings and an ace or some other combination of events i'd like to know how to do the calculations myself.

thanks everyone so much for your continued patience with me.

also just wanted to add i have been a member for almost 4 years and posted before, i dont think the lack of a image post option is because of a new account issue, if that helps in any way

Quote: joanmiller

Thank you so much to everyone for trying to help, I really appreciate it a lot. I'll try to explain without the screenshot and hopefully I make sense.

My biggest problem is that I don't know how to apply the cost of the bet to the calculation of the return to player and therefore can't figure out the house edge.

you are right the bet is $5 but because it stays in play (without any additional player contribution) until either a 'no ace' case or a '3 aces' case i dont actually know what the cost to play is. i mean it costs $5 but the potential for multiple payouts on the initial bet are making it hard for me to understand how to calculate the house edge, and while i thank every one for the help it's really the theory and maths that i need, because if it was for 4 aces or 2 kings and an ace or some other combination of events i'd like to know how to do the calculations myself.

thanks everyone so much for your continued patience with me.

also just wanted to add i have been a member for almost 4 years and posted before, i dont think the lack of a image post option is because of a new account issue, if that helps in any way
link to original post

I was looking around to find out about "cost of play" and I found two examples (one, another). I don't want to say that they give the solution to your problem, but if the area of mathematics is the right one, then I might be able to explain the solution to your question step by step. Please give me a bit more time to prepare it with properly formatted equations.

About posting pictures: I tried to retrace when I received the right to post pictures and my guess is, that it was on my 26th post. It might be that you might need 14 more posts until you will be assigned the "Insert My Picture" button.

Have you seen my workaround? Could you please post your Excel solution to see how you set it up?

I'll try to provide my solution as fast as possible.

I tried to put together a derivation of the cost to play from the basic formula of expected value.
Please ask, if any of my explanations are unclear or have any mistakes.

Starting at the simple case of a binary game with one winning and one losing outcome, I expanded to the general equation of multiple winning options, which is needed for the calculations you intend to perform.



From that equation, based on winnings and losses, I step by step transform to the equation based on payouts, which is needed for your type of exercise.



The last step then is to set the expectation to zero, which is the definition for the fair game, and calculate the cost to play by summing up the expected payout.



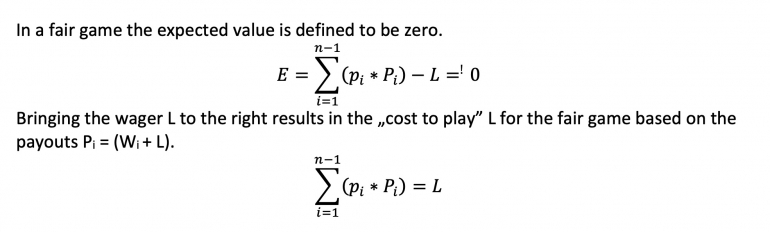
At this point I need information about the payouts from you, but let's first see what we have so far:

For your given exercise we know what the probabilities are and are able to fill them into the cost equation:

p(exactly one ace) = 4/52 * 48/51 approx. 0.072398
p(exactly two aces) = 4/52 * 3/51 * 48/50 approx. 0.004344
p(three aces) = 4/52 * 3/51 * 2/50 approx. 0.000181

(0.072398 * P1 + 0.004344 * P2 + 0.000181 * P3) = cost to play (fair game assumed)

The payouts P1, P2, and P3 are still unclear. Could you please give a hint?

Remark: House edge and the other parameters I will work on, once this equation is clarified.

I'm not completely sure whether my approach does comply with the way you usually solve this kind of exercise but here is my idea of the next steps.
For now I assume as payouts the odds you suggested. I will use the exact inverse of the probabilities.

Please see in my adjusted Excel schema ...
... in red - the probabilities, which remain fixed in all the following calculations.
... in blue - the expectation based on the payouts.
... in green - the "classic" expected value based on winnings and losses.
... in purple - the expected value for a chosen wager and its related house edge.

I will expand on the details, below.





PROBABILITIES (red)
The probabilities have been discussed and I think we agree on these. Columns B, C, and D have the probabilities for single events of aces and no aces which then are multiplied for the final probabilities in column E. The plausibility check in cell E6 makes sure that no probabilities are forgotten and all probabilities in column E add up to 1, as required by definition.

PAYOUTS AND THEIR EXPECTATION (blue)
Here is how the equation of the cost to play corresponds to the Excel schema:



The question, of course, is: "Why is row 2 missing?"
Answer: It is not missing, it is just not explicitly rendered because zero is the neutral element of addition and the annihilating element of multiplication.



We know that we assumed a fair game and that we here calculated the expectation based on the payouts. This result L can be interpreted in the following ways:
L is the expected payout the player would gain if the player was not required to pay any wager.
L is the expected return to the player if the player was not required to pay any wager.
L is the cost to play for the house if the player was not required to pay any wager.

So the house will have to charge the value of L from the player as a wager in order to not lose any money. Eventually it will be the player's cost to play. Nevertheless, it still is a fair game, so the house will neither lose, but more importantly, nor win any money in the long run.

EXPECTED VALUE (green)
Knowing the cost to play, the expected value based on winnings and losses can now be calculated for the fair game. The loss of the player in cell H2 is the wager L, calculated in the previous step. The winnings and losses are determined by subtracting that wager from each of the payouts of the previous step. Multiplying the winnings and losses by their related probabilities and summing all up results in the expected value of zero, as defined for a fair game.

HOUSE EDGE (purple)
The house will want to earn some money from the players so what they can do is increase the wager. In this case I used your suggested wager of $5. The winnings and losses are determined from the payouts of column F, like in the green case, but now wager lost (cell J2) is set to -5. Cell K6 then has the expected value. Dividing this by the (new) wager (absolute value of J2) results in the house edge for this game.

CONCLUSION
Assumed that my sollution is compliant to your approach, you may use this schema as a general tool for this kind of exercises:
0) The schema is neither restricted to four rows , nor to the three columns B, C, and D which help to determine the probabilities. The formulas in columns F through K are uniform and can simply be copied to additional rows. Make sure to adjust the sums (here row 6) to cover all of your rows.
1) Determine all probabilities included in your exercise and put them in column E. Make sure they all add up to 1.
2) Insert all payouts in column F and also give the zero for the complete loss of the wager.
3) The expected pays in column G are calcualted automatically, as well as the "cost to play" at the bottom of column G (here cell G6).
4) Columns H and I are calculated automatically. Make sure that the sum at the bottom of column I (here cell I6) is zero, since the fair game is assumed.
5) Columns J and K are calculated automatically. Play around with the wager in cell J2 to see the changes in the expected value (here cell K6) and in the house edge (here cell K7).

Quote: ThomasK

Quote: joanmiller

Thank you so much to everyone for trying to help, I really appreciate it a lot. I'll try to explain without the screenshot and hopefully I make sense.

My biggest problem is that I don't know how to apply the cost of the bet to the calculation of the return to player and therefore can't figure out the house edge.

you are right the bet is $5 but because it stays in play (without any additional player contribution) until either a 'no ace' case or a '3 aces' case i dont actually know what the cost to play is. i mean it costs $5 but the potential for multiple payouts on the initial bet are making it hard for me to understand how to calculate the house edge, and while i thank every one for the help it's really the theory and maths that i need, because if it was for 4 aces or 2 kings and an ace or some other combination of events i'd like to know how to do the calculations myself.

thanks everyone so much for your continued patience with me.

also just wanted to add i have been a member for almost 4 years and posted before, i dont think the lack of a image post option is because of a new account issue, if that helps in any way
link to original post

I was looking around to find out about "cost of play" and I found two examples (one, another). I don't want to say that they give the solution to your problem, but if the area of mathematics is the right one, then I might be able to explain the solution to your question step by step. Please give me a bit more time to prepare it with properly formatted equations.

About posting pictures: I tried to retrace when I received the right to post pictures and my guess is, that it was on my 26th post. It might be that you might need 14 more posts until you will be assigned the "Insert My Picture" button.

Have you seen my workaround? Could you please post your Excel solution to see how you set it up?

I'll try to provide my solution as fast as possible.
link to original post

Gosh Thomas, I really have faith restored in humanity when I see people like yourself, so helpful and generous with your time and effort. I can't thank you enough but thank you!
I watched the two videos you linked to and while cost to play and house edge is easy to calculate for a one-time bet, the issue for me is that the bet remains. to make it easier to follow i'll respond to your wonderfully helpful and generous posts below in a separate quoted response.

Quote: ThomasK

I tried to put together a derivation of the cost to play from the basic formula of expected value.
Please ask, if any of my explanations are unclear or have any mistakes.

Starting at the simple case of a binary game with one winning and one losing outcome, I expanded to the general equation of multiple winning options, which is needed for the calculations you intend to perform.

expected value g

[/spoiler]

From that equation, based on winnings and losses, I step by step transform to the equation based on payouts, which is needed for your type of exercise.

[spoiler=from win|loss to g]

The last step then is to set the expectation to zero, which is the definition for the fair game, and calculate the cost to play by summing up the expected payout.

[spoiler=cost to g][/spoiler]

At this point I need information about the payouts from you, but let's first see what we have so far:

For your given exercise we know what the probabilities are and are able to fill them into the cost equation:

p(exactly one ace) = 4/52 * 48/51 approx. 0.072398
p(exactly two aces) = 4/52 * 3/51 * 48/50 approx. 0.004344
p(three aces) = 4/52 * 3/51 * 2/50 approx. 0.000181

(0.072398 * P1 + 0.004344 * P2 + 0.000181 * P3) = cost to play (fair game assumed)

The payouts P1, P2, and P3 are still unclear. Could you please give a hint?

Remark: House edge and the other parameters I will work on, once this equation is clarified.
link to original post

so for the p1, p2 and p3 id like to have an excel spreadsheet that allows me to change these payouts and see the resulting effect on the house edge

Quote: ThomasK

I'm not completely sure whether my approach does comply with the way you usually solve this kind of exercise but here is my idea of the next steps.
For now I assume as payouts the odds you suggested. I will use the exact inverse of the probabilities.

Please see in my adjusted Excel schema ...
... in red - the probabilities, which remain fixed in all the following calculations.
... in blue - the expectation based on the payouts.
... in green - the "classic" expected value based on winnings and losses.
... in purple - the expected value for a chosen wager and its related house edge.

I will expand on the details, below.

g]

Please see here the formulas behind the g

[/spoiler]

PROBABILITIES (red)
The probabilities have been discussed and I think we agree on these. Columns B, C, and D have the probabilities for single events of aces and no aces which then are multiplied for the final probabilities in column E. The plausibility check in cell E6 makes sure that no probabilities are forgotten and all probabilities in column E add up to 1, as required by definition.

PAYOUTS AND THEIR EXPECTATION (blue)
Here is how the equation of the cost to play corresponds to the Excel schema:

g]

The question, of course, is: "Why is row 2 missing?"
Answer: It is not missing, it is just not explicitly rendered because zero is the neutral element of addition and the annihilating element of multiplication.

[spoiler=Why payout zero is not g]

We know that we assumed a fair game and that we here calculated the expectation based on the payouts. This result L can be interpreted in the following ways:
L is the expected payout the player would gain if the player was not required to pay any wager.
L is the expected return to the player if the player was not required to pay any wager.
L is the cost to play for the house if the player was not required to pay any wager.

So the house will have to charge the value of L from the player as a wager in order to not lose any money. Eventually it will be the player's cost to play. Nevertheless, it still is a fair game, so the house will neither lose, but more importantly, nor win any money in the long run.

EXPECTED VALUE (green)
Knowing the cost to play, the expected value based on winnings and losses can now be calculated for the fair game. The loss of the player in cell H2 is the wager L, calculated in the previous step. The winnings and losses are determined by subtracting that wager from each of the payouts of the previous step. Multiplying the winnings and losses by their related probabilities and summing all up results in the expected value of zero, as defined for a fair game.

HOUSE EDGE (purple)
The house will want to earn some money from the players so what they can do is increase the wager. In this case I used your suggested wager of $5. The winnings and losses are determined from the payouts of column F, like in the green case, but now wager lost (cell J2) is set to -5. Cell K6 then has the expected value. Dividing this by the (new) wager (absolute value of J2) results in the house edge for this game.

CONCLUSION
Assumed that my sollution is compliant to your approach, you may use this schema as a general tool for this kind of exercises:
0) The schema is neither restricted to four rows , nor to the three columns B, C, and D which help to determine the probabilities. The formulas in columns F through K are uniform and can simply be copied to additional rows. Make sure to adjust the sums (here row 6) to cover all of your rows.
1) Determine all probabilities included in your exercise and put them in column E. Make sure they all add up to 1.
2) Insert all payouts in column F and also give the zero for the complete loss of the wager.
3) The expected pays in column G are calcualted automatically, as well as the "cost to play" at the bottom of column G (here cell G6).
4) Columns H and I are calculated automatically. Make sure that the sum at the bottom of column I (here cell I6) is zero, since the fair game is assumed.
5) Columns J and K are calculated automatically. Play around with the wager in cell J2 to see the changes in the expected value (here cell K6) and in the house edge (here cell K7).
link to original post

Just to say again THANK YOU THOMASK for all this work, is there some way of giving you credit for the work (like a vote process on the forum?)

I have played around with your excel output and I think we are really close, if not already there and I just can't see it.

The way I have it now is that I have removed columns G, H, I & J and changed the payout in F to be what the player gets for the event so in F2 I have (-1) because they lose what ever the wager is if this event occurs? then in K I have F*E to get the contribution of each outcome to the house edge. Do you think this is correct?

I have the following payouts in F:
-1
6
100
200
for a house edge of 1.81%
does this represent a bet that is placed and lasts until either the no ace or 3 ace condition is met and is paid out at each winning event (ie you get 6:1 on the first ace, 100:1 on the second and 200:1 for the third)?

Quote: joanmiller

Quote: ThomasK

[...]

CONCLUSION
Assumed that my sollution is compliant to your approach, you may use this schema as a general tool for this kind of exercises:
0) The schema is neither restricted to four rows , nor to the three columns B, C, and D which help to determine the probabilities. The formulas in columns F through K are uniform and can simply be copied to additional rows. Make sure to adjust the sums (here row 6) to cover all of your rows.
1) Determine all probabilities included in your exercise and put them in column E. Make sure they all add up to 1.
2) Insert all payouts in column F and also give the zero for the complete loss of the wager.
3) The expected pays in column G are calcualted automatically, as well as the "cost to play" at the bottom of column G (here cell G6).
4) Columns H and I are calculated automatically. Make sure that the sum at the bottom of column I (here cell I6) is zero, since the fair game is assumed.
5) Columns J and K are calculated automatically. Play around with the wager in cell J2 to see the changes in the expected value (here cell K6) and in the house edge (here cell K7).
link to original post

Just to say again THANK YOU THOMASK for all this work, is there some way of giving you credit for the work (like a vote process on the forum?)

I have played around with your excel output and I think we are really close, if not already there and I just can't see it.

The way I have it now is that I have removed columns G, H, I & J and changed the payout in F to be what the player gets for the event so in F2 I have (-1) because they lose what ever the wager is if this event occurs? then in K I have F*E to get the contribution of each outcome to the house edge. Do you think this is correct?

I have the following payouts in F:
-1
6
100
200
for a house edge of 1.81%
does this represent a bet that is placed and lasts until either the no ace or 3 ace condition is met and is paid out at each winning event (ie you get 6:1 on the first ace, 100:1 on the second and 200:1 for the third)?
link to original post

First of all, thank you joanmiller for your kind feedback. I don't think there's any need for any extra credit. It actually has been my pleasure, because I had to learn about "cost to play", I had to think about the mathematics from a different angle, and I had a reason to "Excel around".

About your adjustments: I understand that you would like to have one crisp way to the solution. The thing is, that there are two ways to calculate the game: One based on payouts, the other based on winnings and losses. Both are equivalent, as I tried to show, but they cannot be intermixed.
So at least the steps blue and purple, are necessary to find the parameters of this game:

BLUE
Column F has payouts. If you think of the game as an imaginary slot machine, you would have a certain "coin in" and in the successful cases the machine would cash out the values given in cells F3 to F5.
But in the not succesfull case the machine will not cash out -1. It will rather cash out nothing, the zero in F2. And this zero remains constant for any coin in. Any slot machine will pay nothing (the zero) in case of the player losing, indepenent of the coins the machine might demand for a single play.

So what is the catch?
Columns F and G are used to calculate the expected amount (cell G6) this machine will cash out on average for a single play. Independent of the coin in, as we saw above. Even if the player could play it for free (zero!).
But what we now can infer is that if we charged exactly this expected amount from the player, neither the player nor we would lose (nor gain) any money from that machine, because it would be a fair game.
To see that this actually is true, the following green section calculates the "classical" expected value from wins and losses.

GREEN
Here the payouts are converted to wins and losses by subtracting the coin in (or wager) from the payouts. Only here the wager now is visible for the first time in cell H2, because we subtract the wager from zero. This "green" wager is a special one: We use the cost to play for the fair game which eventually results in zero expectation in cell I6.
Besides the verification of the fair game this green section also is the template for the more general purple section.

PURPLE
Here I have to apologize for a mistake in the formulas of column J!
The wins of course are not the same as those in column H but rather have to be calculated analogous to those in column H, by subtracting the wager (absolute value of now cell J2) from the payouts (still in column F).
Remark: Of course you can simply add J2 to the values of column F because J2 already is negative. But I wanted to emphasize that you subtract the wager from the payouts.


Cell J2 therefore is the proper place to put your wager of 1 as the losing amount of -1. That is because only in the "classical" expectation the wager is visible.

OPTIMIZATION
For a dense, crisp Excel schema you may remove columns H and I because they only verify that "cost to play" and "fair game" lead to an expectation of zero.
Column G might be removed if you didn't need the wager for the fair game, or cost to play, as a result.

SUMMARY
Please refer back to the points of the conclusion in my previous post.
About 2)
Put the payouts in column F and leave the "payout" for the losing condition zero (here cell F2).
About 5)
Put your wager as a negative value in the losing condition (here cell J2).
The expected value and the house edge are displayed at the bottom of column K (here cell K6 and cell K7).





To be answered: The Question about sequential pays ...

Quote: joanmiller

[...]

I have the following payouts in F:
-1
6
100
200
for a house edge of 1.81%
does this represent a bet that is placed and lasts until either the no ace or 3 ace condition is met and is paid out at each winning event (ie you get 6:1 on the first ace, 100:1 on the second and 200:1 for the third)?
link to original post

As charliepatrick and DogHand replied before, paying each winning event does not change any of the parameters of the game.
Again think of the game as an imaginary slot machine. Imagine further that the machine's mechanism does not draw the individual cards successively but rather it selects one of the four branches (see rows 2 through 5) randomly according to the probabilities given in column E.

What the machine now displays to the player is the sequence of cards corresponding to the branch selected. Here the four branches:
* Displays a card that is not an ace - player loses, no payout (=0).
* Displays an ace, player is paid 6, then a card that is not an ace, no further pay - player wins (=6).
* Displays one ace, player is paid 6, another ace, player is paid 94, then a card that is not an ace, no further pay - player wins (=6+94=100).
* Dispalys one ace, player is paid 6, another ace, player is paid 94, finally a third ace, player is paid 100 - player wins (=6+94+100=200).

As you can see, the payouts of each branch have to be split into portions that sum up to the total payout of the branch.

In the Excel scheme the three total payouts can be substituted by these sums. Nothing else will change in any of the other values.





You may play around and try to pay 6, 100, and 200 for each ace instead. The total payouts for the branches will of course change and the new paytable would have 6, 106, and 306, resulting in an house edge of -4.97%

Thank you again ThomasK for your response and for helping me so much!

So I am a little confused about the payouts but is it correct to say that if J has 5, 105 & 305, the player is getting $25 for 1 ace, $525 (on top of the first $25) for the 2nd ace and $1525 (on top of the previous 2 payouts) for the 3rd ace? (for a $5 bet) Or is it that the actual payout is what the player gets from F and if so is the logic the same as I just mentioned, as in each payout is in addition to the previous, such that if a player got 3 aces they payout would be 6+106+306 (418) pieces?

For these payouts in J i get a positive house edge of 4.98%.

Kindest regards and thank for your patience and persistence.

I'm also now curious, if there is a way to add a progressive jackpot to this? How do we pay out on each ace and also keep some of the original $5 aside for contribution to a progressive jackpot payout for the 3 aces condition? How do we calculate how much should come out of the original $5?

Quote: joanmiller

Thank you again ThomasK for your response and for helping me so much!

So I am a little confused about the payouts but is it correct to say that if J has 5, 105 & 305, the player is getting $25 for 1 ace, $525 (on top of the first $25) for the 2nd ace and $1525 (on top of the previous 2 payouts) for the 3rd ace? (for a $5 bet) Or is it that the actual payout is what the player gets from F and if so is the logic the same as I just mentioned, as in each payout is in addition to the previous, such that if a player got 3 aces they payout would be 6+106+306 (418) pieces?

[...]

link to original post

Hmm, I somehow understand the confusion. I hope I'm able to explain it more clearly.

There are two things to bear in mind when using this Excel schema:
1) Column F has payouts, column J has winnngs and losses.
2) For the case of successive pays, stay in the one row only, which defines the situation you're analyzing.

DETAILS

1) Column F has payouts, column J has winnngs and losses.

Payouts are the complete amount the player gets. This amount includes the initial wager.
Examples are payouts of a slot machine or prop bets at the craps table that pay "... for 1".
In the case of a loss the player receives nothing (zero), not even the initial wager.

Winnings are of the kind "... to 1" as you find them on the pass line bet in craps paying 1 to your 1 initial wager or most prominently at roulette where for example red pays 1 to 1, a dozen pays 2 to 1 or the straight up number pays 35 to 1. The winning is the amount without the wager but the player also receives back the initial wager.
In this context the loss is expressed as the minus wager.

During any discussion it must be clear whether either payouts or winnings are the basis of calculation. This determines whether column F or column J will take the given amounts.
Once this is established, each can be converted to the other:

Payouts have to be put in column F. The losing condition there has to be the constant zero (here cell F2). Values of column J are then derived by subtracting the initial wager. As a plausibility test, the losing condition in columnn J has to have the minus wager (here cell J2). That's what I had in my explanation so far.

If winnings are the basis of the discussion, then the initial amounts have to be put in column J. The losing condition then has to be the minus initial wager (here cell J2).
The values of column F therefore now have to be calculated from column J by adding the wager. The plausibility test here is that the losing condition has to result in an amount of zero (here cell F2).

2) For the case of successive pays, stay in the one row only which defines the situation you're analyzing.

Paying intermediate results is not any sum of rows of the Excel schema.
The consecutive pays rather are inherently built into each of the individual rows, i.e. the branches of the overall random experiment.

I'll use the values of your previous post (-1 6 100 200) for this example:
Let's define:
The player wagers $1.
This wager is collected immediately by the dealer so all amounts to come will be payouts (not winnings, see above): $6, $100, $200.
Now that we know that we are talking about payouts, we know that we have to put the amounts in cells F3, F4, and F5.
Cell F2 has the losing condition and remains the constant zero.

Now talking about 3 aces in sequence, we remain in row 5 of the Excel schema. We know we want to have paid a total of $200 after the third ace.
You can see the 200 in cell F5.
As a special feature we want to pay a portion of these $200 directly after each of the aces is dealt.
We still remain in row 5 and especially in cell F5: Let's define the portions $X + $Y + $Z = $200.
X, Y, and Z may be set arbitrarily BUT we have additional conditions.

For exactly 2 aces in sequence, we want to pay $100. This branch is defined in row 4 of the Excel schema, where we now remain in.
You can see the 100 in cell F4.
We want to pay portions ot these $100 after each ace is dealt, so we define the portions $X + $Y = $100.
The variables X and Y are intentionally the same as those above, because they are the connection and the additional condition between the 3 aces and the 2 aces branches. Here X and Y still may be set arbitrarily. So we need a third condition:

For exactly 1 ace we want to pay $6.
We do not need portions here any more because the single ace has its own single payout.
Nevertheless we can now define $X = $6.
This is the last connection between the three branches.

Calculating backwards, we now are able to determine the portions payed to player during any sequence without violating any of our initially defined payout goals of $6, $100, and $200:

$X = $6

$X + $Y = $100
$6 + $Y = $100
........$Y = $100 - $6
........$Y = $94

$X + $Y + $Z = $200
$6 + $94 + $Z = $200
..................$Z = $200 - $6 - $94
..................$Z = $100

However, the values 94 and 100 are not explicitly visible in the Excel schema but they are implicitly built into the cells F4, and F5.

Quote: joanmiller

[...]

For these payouts in J i get a positive house edge of 4.98%.

[...]

link to original post

I'm sorry about my confusion here. It is the switching between the player's view and the house's view that lets me mess with the signs.
Of course you are completely right: It is the house edge, i.e. the house has the advantage, so the value must be positive.
(Remark: If it was negative, the bettor would be an advantage player ...)

The player, however, has a negative expectation which would correspond to the same magnitude of the house edge but with a negative sign.
I will definitely have to pay better attention to this subtlety.

Quote: joanmiller

[...]

I'm also now curious, if there is a way to add a progressive jackpot to this? How do we pay out on each ace and also keep some of the original $5 aside for contribution to a progressive jackpot payout for the 3 aces condition? How do we calculate how much should come out of the original $5?
link to original post

I guess you are the pro when it comes to progressives.
Am I mistaken if my understanding so far is that only the wager, or coin in, contributes to the progressive, not the payouts?
If this was the case then, as my first guess, nothing would change concerning the calculations so far.
Since we are talking about the 3 aces condition only, winning the progressive would be triggered by this branch only, which is our row 5 in the Excel schema.

Are there more details to be taken into account?

You are so patient, I hope I'm not testing my luck, but I think you have really helped me get this. I just want to ask you to check my understanding if possible please; is the payout (assuming the dealer pays after each ace is dealt and $6 has already been paid for the first ace) going to be $94 on the second ace or $100?

Quote: ThomasK

Quote: joanmiller

[...]

I'm also now curious, if there is a way to add a progressive jackpot to this? How do we pay out on each ace and also keep some of the original $5 aside for contribution to a progressive jackpot payout for the 3 aces condition? How do we calculate how much should come out of the original $5?
link to original post

I guess you are the pro when it comes to progressives.
Am I mistaken if my understanding so far is that only the wager, or coin in, contributes to the progressive, not the payouts?
If this was the case then, as my first guess, nothing would change concerning the calculations so far.
Since we are talking about the 3 aces condition only, winning the progressive would be triggered by this branch only, which is our row 5 in the Excel schema.

Are there more details to be taken into account?
link to original post

Oh good heavens no, I'm no pro at all if anything my math is regressed!

So the jackpot/progressive would be funded by the coin in, but I thought we could simply reduce the payout of one or all of the payouts to calculate the house edge on the 3 ace jackpot. You're right though that seems unnecessary, so how could we take into account the coin in funding the progressive? My initial thought was we reduce the -1 to -0.8 or so and put that $0.20 towards the progressive (and then adjust the other payouts accordingly) but then does that mean if they get 1 or 2 (or even 3 aces) they haven't contributed at all to the progressive. Sorry thinking out loud, hope that makes sense.

Quote: joanmiller

You are so patient, I hope I'm not testing my luck, but I think you have really helped me get this. I just want to ask you to check my understanding if possible please; is the payout (assuming the dealer pays after each ace is dealt and $6 has already been paid for the first ace) going to be $94 on the second ace or $100?
link to original post

No, no, that's all right. From your questions I will know whether I have been able to explain in an understandable manner.

The idea actually is that the dealer will pay $6 after the first ace and $94 after the second ace.
If the next (third) card was not an ace, this hand would be over and the player would have won a total of $100, just as we defined for this branch of the game of exactly two aces.

If however the third card was another ace, the dealer would pay an additional $100 after this third ace and the player would then have won a total of $200, just as we defined for the case of three consecutive aces.



About your next question on the progressive: Please allow for some extra time for pondering before I will answer this.