Ant on the rubber band problem.

I get asked this problem every once in a while, and I've never been able to solve it. Maybe somebody who is good with partial differential equations can help. Here is what you have:

1. There is a 1 km rubber band.
2. An ant starts at one end.
3. The ant moves towards the other end at a speed of 1 cm./sec..
4. The rubber band stretches at a rate of 1 km./sec..

How long does it take for the ant to reach the other end?

Here is about as far I get with this, which admittedly isn't much.

Let the ant's position at the beginning be 0 at time 0, with one end of the rubber band fixed to that point.
Let f(t) be the ant's distance from the starting point at time t.
f'(t) is the ant's speed at time t.

The speed is 1 + 100,000*ratio of progress (where the ratio of progress is how much of the rubber band the ant has crossed).

So, I think, we've got f'(t) = 1 + 100000*f(t)/(100000*(1+t))

My calculus skills are just too rusty to get past this point, not that they were ever outstanding to begin with. If I could solve for f(t) then I think I could get the rest of the way easily by finding the point at which the ant's position is equal to the end point (100000*(1+t)).

This is where I need to use my phone a friend. Can anybody get me further along the rubber band of this problem? ME? DG? Doc?

Can it be proven he even gets to the other end? More specifically, does he ever reach a point where the end is receding from him more slowly than 1 cm/sec? Can you solve for this point?

Quote: 7outlineaway

Can it be proven he even gets to the other end? More specifically, does he ever reach a point where the end is receding from him more slowly than 1 cm/sec? Can you solve for this point?

Yes, the ant will reach the end, after a very long time. As a ratio of the rubber band traveled, the ant makes progress with every step.

That makes for a good side question about when the distance to the end starts to decrease with time. I would imagine it isn't until somewhere in the last minute or so.

Quote: Wizard

Yes, the ant will reach the end, after a very long time. As a ratio of the rubber band traveled, the ant makes progress with every step. This ratio keeps increasing too, so eventually it must get to 1.

That makes for a good side question about when the distance to the end starts to decrease with time. I would imagine it isn't until somewhere in the last minute or so.

Isn't this just an infinite series that sums to 1?

I'm happy to say that I have ZERO IDEA of what you're talking about. VERY happy!

Well, Wizard, it has been a heck of a long time since I have tried to solve a differential equation, and my brain has atrophied quite a bit. I had to go to a reference book for some help on the technique. This is what I came up with, and I still wish there were an easy way to post equations on this forum.

Starting from your equation, I simplify it and get:



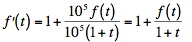
I believe the solution to this differential equation is:



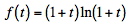
Then, considering the point when the ant reaches the end point, we can solve for the time required in seconds:



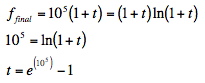
Even if this answer is correct, my calculator will not display the answer.

Is the rubberband infinitely elastic? That is, will it (if it were a real object) eventually reach a maximum length, then stop, or for the purposes of this exercise, will it continue to stretch forever?

If infinite, I don't think the ant makes up the difference. Every 100,000 seconds, the ant will cover 1 km. But in that time, the other end of the rubberband will be another 99,999 km ahead of him. This growth is constant and infinite, so the ant will never catch up. What am I missing?

As the band stretches, the ant is moved along it as well... e.g it stays the same percentage on the band.

Why not solve for smaller numbers first?

Ayecarumba, I think what you are missing is that as the ant crawls, the piece of rubber he is standing on is moving because of the stretch. His 1 cm/s walk is in relation to that piece of the rubber band. The further he moves along it, the faster he moves. As he approaches the end, he is traveling nearly 1 km/sec. I think his final step has him traveling 1.00001 km/s, or 1 cm/s faster than the moving end of the rubber band.

It takes him a long, long time to get there, though.

An yes, the assumption is that there is infinite stretch available but that neither the weight of the rubber band nor the weight of the ant cause it to sag.

Basically the end of the band is receding, but the rate of change of that distance decreases.