Surface to air missile puzzle
Thread Rating:
Poll
| No votes (0%) | |||
| No votes (0%) | |||
 | 1 vote (16.66%) | ||
| | 1 vote (16.66%) | ||
| | 1 vote (16.66%) | ||
| | 2 votes (33.33%) | ||
| No votes (0%) | |||
| | 1 vote (16.66%) | ||
| | 3 votes (50%) | ||
| | 4 votes (66.66%) |
6 members have voted
November 15th, 2020 at 7:42:47 PM
permalink
This one is definitely worth of it's own thread. It pushes against the limits of my math ability.
An airplane is directly 8 miles overhead from you, traveling at a speed of 600 mph. The plane maintains the same altitude and same direction. At that moment, you fire surface-to-air missile at it. The missile always travels at a speed of 2,000 mph and always points directly at the airplane.
How far away will the wreckage fall, assuming it will fall directly below the point of impact?
For full credit, I want to see an expression for the answer and solution.
An airplane is directly 8 miles overhead from you, traveling at a speed of 600 mph. The plane maintains the same altitude and same direction. At that moment, you fire surface-to-air missile at it. The missile always travels at a speed of 2,000 mph and always points directly at the airplane.
How far away will the wreckage fall, assuming it will fall directly below the point of impact?
For full credit, I want to see an expression for the answer and solution.
Last edited by: Wizard on Nov 15, 2020
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 15th, 2020 at 8:24:42 PM
permalink
Quote: WizardThis one is definitely worth of it's own thread. It pushes against the limits of my math ability.
An airplane is directly 8 miles overhead from you, traveling at a speed of 600 mph. At that moment, you fire surface-to-air missile at it. The missile always travels at a speed of 2,000 mph and always points directly at the airplane.
How far away will the wreckage fall, assuming it will fall directly below the point of impact?
For full credit, I want to see an expression for the answer and solution.
Here's my answer:
Since you didn't specify the airplane's flight vector, I'll assume it is flying vertically away from you. Thus, the missile will strike the plane at a time of t = 8 miles/ (2000 - 600) mph = 1/175 hrs = 20.57... seconds, and the wreckage will fall right on top of you, killing you.
Dog Hand
November 15th, 2020 at 9:01:03 PM
permalink
Quote: DogHandHere's my answer:
Since you didn't specify the airplane's flight vector, I'll assume it is flying vertically away from you. Thus, the missile will strike the plane at a time of t = 8 miles/ (2000 - 600) mph = 1/175 hrs = 20.57... seconds, and the wreckage will fall right on top of you, killing you.
Dog Hand
That is pretty funny. I added to the wording that the plane maintains the same altitude and direction.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 16th, 2020 at 10:00:26 AM
permalink
Quote: WizardHow far away will the wreckage fall, assuming it will fall directly below the point of impact?
It isn't that hard to determine how far in terms of horizintal distance the airplane would travel.
8 miles = about 12.875 km
Assume the acceleration due to gravity is a constant 9.81 m/sec2
The time it takes to fall is t = sqrt(2 x 12,875 / 9.81) = about 51.23 seconds
The horizontal distance = 51.23 / 3600 hours x 600 miles/hour = about 8.54 miles.
It's a little bit above my normal math pay grade; I haven't worked with DEs in decades. Here's what I have so far:
Let xt and yt be the missile's location at time t in seconds; all distances are in miles
x0 = y0 = 0
At time t, the airplane's location is (600 t/3600, 8), or (t/6, 8)
The angle at time t, measured from the positive-x direction toward the positive-y direction, is Anglet = tan-1((8 - yt) / (t/6 - xt)
The missile's velocity = 2000/3600 miles/second = 5/9
δyt/dt = 5/9 sin(Anglet) = 5/9 ((8 - yt) / sqrt((8 - yt)^2 + (t/6 - xt)^2)))
δxt/dt = 5/9 cos(Anglet) = 5/9 ((t/6 - xt) / sqrt((8 - yt)^2 + (t/6 - xt)^2)))
November 16th, 2020 at 10:40:26 AM
permalink
I just want to make it perfectly clear I'm not asking for the distance from the missile launcher to the point of impact in the sky. I am asking for the horizontal distance between the missile launcher and the point on the ground directly below the point of impact.
It would be easy to get a very good estimate of the answer in a spreadsheet. However, I'm looking for a mathematical solution.
Here is an integral you may need, which you could also easily look up.
1/sqrt(1+x2) dx = ln|x + sqrt(1+x2)|
It would be easy to get a very good estimate of the answer in a spreadsheet. However, I'm looking for a mathematical solution.
Here is an integral you may need, which you could also easily look up.
1/sqrt(1+x2) dx = ln|x + sqrt(1+x2)|
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 16th, 2020 at 1:19:47 PM
permalink
Could it be I've stumped the math geniuses of the forum?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 16th, 2020 at 1:26:37 PM
permalink
Quote: WizardCould it be I've stumped the math geniuses of the forum?
This appears to be the same question as the greyhound and the hare, which I remember working out in Calc 2 in college. Have not had time to sit down with it.
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
November 16th, 2020 at 1:32:51 PM
permalink
Quote: unJonThis appears to be the same question as the greyhound and the hare, which I remember working out in Calc 2 in college. Have not had time to sit down with it.
I will allow for extra time with this one. I spent a good part of the weekend on it, to be honest.
The spoiler will reveal the path of the missile and will give away the approximate answer. Don't click it if you don't want to know.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 16th, 2020 at 8:53:18 PM
permalink
i doubt any of the scatter pattern would be diretly below impact point, else airshows would be different.
Predictable? One of the first pilots killed when Japanese fighter pilots dove into parachuting Americans was a pilot who died from a .38 calibre pistol wound!
Predictable? One of the first pilots killed when Japanese fighter pilots dove into parachuting Americans was a pilot who died from a .38 calibre pistol wound!
November 16th, 2020 at 8:53:19 PM
permalink
i doubt any of the scatter pattern would be diretly below impact point, else airshows would be different.
Predictable? One of the first pilots killed when Japanese fighter pilots dove into parachuting Americans was a pilot who died from a .38 calibre pistol wound!
Predictable? One of the first pilots killed when Japanese fighter pilots dove into parachuting Americans was a pilot who died from a .38 calibre pistol wound!
November 16th, 2020 at 11:06:56 PM
permalink
1.9780219 miles
Purely numerical solution.
I don't even know where to start, mathematically. I'm sure it would have been no problem when I was in high school, but it makes my head hurt now.
I heart Crystal Math.
November 17th, 2020 at 5:32:07 AM
permalink
Quote: CrystalMath
1.9780219 miles
Purely numerical solution.
I don't even know where to start, mathematically. I'm sure it would have been no problem when I was in high school, but it makes my head hurt now.
I've been wrong before, but I disagree. I worked out a numerical solution in Excel and you can see from the graph below, my answer at least 2.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 17th, 2020 at 9:05:02 AM
permalink
Quote: FleaStiffi doubt any of the scatter pattern would be diretly below impact point, else airshows would be different.
It can't be, as the missile is always pointing toward the target. The only way the missile could be directly underneath the impact point is if the target was stationary and the missile was fired from directly underneath it.
I haven't gotten the "House lightbulb moment" for solving this one yet; I still have two partial derativates (where the horizontal and vertical velocity vectors are each in terms of the current horizontal and vertical location).
Quote: CrystalMath
1.9780219 miles
Purely numerical solution.
I don't even know where to start, mathematically. I'm sure it would have been no problem when I was in high school, but it makes my head hurt now.
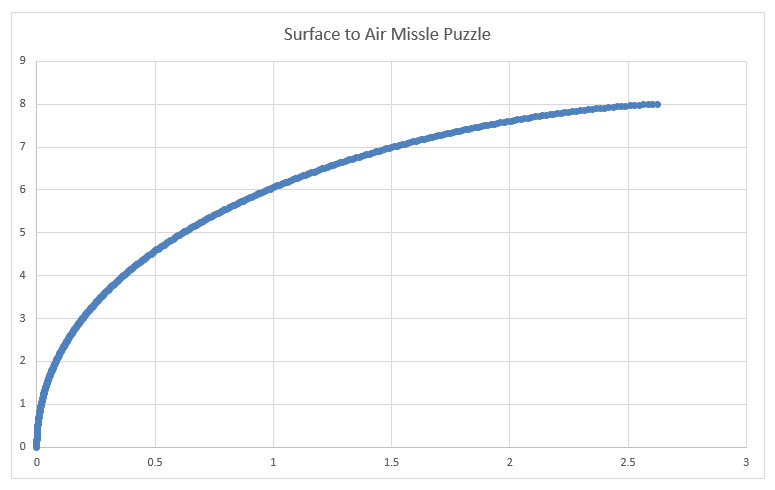
...the Wizard's graph; using Excel, I get a contact point around 2.6375 miles down range.
Note that, assuming what's left of the plane maintains a forward velocity of 600 MPH, and assuming its vertical velocity is a constant 32 feet/sec^2, it will take about 51 seconds to hit the ground form an altitude of 8 miles, so its wreckage point is an additional 8.5 miles away.
November 17th, 2020 at 9:49:20 AM
permalink
The next time I ask this, I won't ask about the distance to the wreckage, as I don't want to confuse the issue with the horizontal velocity of the wreckage.
Let the question be what is the horizontal distance from the missile launcher to the point on the ground directly below the point of impact eight miles high.
I agree. Still looking for a mathematical solution though.
Let the question be what is the horizontal distance from the missile launcher to the point on the ground directly below the point of impact eight miles high.
Quote: ThatDonGuy
I get a contact point around 2.6375 miles down range.
I agree. Still looking for a mathematical solution though.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 17th, 2020 at 1:42:56 PM
permalink
Quote: WizardI agree. Still looking for a mathematical solution though.
Still trying to figure one out.
November 17th, 2020 at 2:42:40 PM
permalink
Are we assuming the Earth is flat? Or do we need to account for curvature of the Earth?
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
November 18th, 2020 at 5:26:49 AM
permalink
Quote: gordonm888Are we assuming the Earth is flat? Or do we need to account for curvature of the Earth?
You may assume it's flat.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 18th, 2020 at 7:24:35 AM
permalink
Quote: ThatDonGuyStill trying to figure one out.
...but I'm still trying to wrap my head around it. If there's an easier one, I'd like to see it.
However, the solution appears to be that the missile makes contact in 1440/91 seconds, so the airplane's horizontal distance is 1440/91 sec x 600/3600 miles/sec = 240/91 miles (about 2.63736),
November 18th, 2020 at 9:39:13 AM
permalink
Quote: ThatDonGuy
...but I'm still trying to wrap my head around it. If there's an easier one, I'd like to see it.
However, the solution appears to be that the missile makes contact in 1440/91 seconds, so the airplane's horizontal distance is 1440/91 sec x 600/3600 miles/sec = 240/91 miles (about 2.63736),
I agree, it's 240/91. Still waiting to see a solution for full credit.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 18th, 2020 at 12:12:42 PM
permalink
I have to confess, I haven't even attempted to solve this problem. (I think I have become tired of my head frequently failing to do what it is supposed to be able to do, so maybe I avoid challenges!) When I first read the problem, my mind made a leap (assumption) that the missile path would be a parabola, but I don't really have much basis for that other than feeble "intuition."
I did like the looks of the Wizard's graph of the trajectory. While I was stationed at White Sands Missile Range fifty years ago, I watched quite a few launches, most of which were set to fly a programmed route, while a few were trying to intercept drones (testing the full system of missile, target-tracking system, missile-tracking system, and guidance). From ground level, I could not detect any visual difference between those paths and the Wizard's graph. About the only comment I can offer from that experience is that the assumption of a constant velocity missile would not represent the norm -- those things begin at rest, experience a period of very-high acceleration, and just maybe a period of constant velocity prior to intercept.
I did like the looks of the Wizard's graph of the trajectory. While I was stationed at White Sands Missile Range fifty years ago, I watched quite a few launches, most of which were set to fly a programmed route, while a few were trying to intercept drones (testing the full system of missile, target-tracking system, missile-tracking system, and guidance). From ground level, I could not detect any visual difference between those paths and the Wizard's graph. About the only comment I can offer from that experience is that the assumption of a constant velocity missile would not represent the norm -- those things begin at rest, experience a period of very-high acceleration, and just maybe a period of constant velocity prior to intercept.
November 18th, 2020 at 12:54:17 PM
permalink
Quote: DocI have to confess, I haven't even attempted to solve this problem. (I think I have become tired of my head frequently failing to do what it is supposed to be able to do, so maybe I avoid challenges!) When I first read the problem, my mind made a leap (assumption) that the missile path would be a parabola, but I don't really have much basis for that other than feeble "intuition."
I did like the looks of the Wizard's graph of the trajectory. While I was stationed at White Sands Missile Range fifty years ago, I watched quite a few launches, most of which were set to fly a programmed route, while a few were trying to intercept drones (testing the full system of missile, target-tracking system, missile-tracking system, and guidance). From ground level, I could not detect any visual difference between those paths and the Wizard's graph. About the only comment I can offer from that experience is that the assumption of a constant velocity missile would not represent the norm -- those things begin at rest, experience a period of very-high acceleration, and just maybe a period of constant velocity prior to intercept.
My father went to the White Sands Missile Range a lot when I was kid. He had a very high security clearance, so couldn't say much about what he did. However, I do know his expertise was in anti-missile missiles. In particular, how to find a missile in air, as evidence by the rocked flair. He knew a great deal about the signature of the flame various things gave off when they burned, especially rocket fuel, including the kind that propels missiles.
I, of course, am not saying what you said is incorrect. However, I had the impression from my father that the way his tests went is when an enemy missile was detected some quick computer calculations were made about where to aim the anti-missile and then let that anti-missile find the target exactly by the rocket flair.
I wonder if you two might have met at some point.
The opening scene in Octopussy, where an anti-plane missile is fired at Bond's plane, demonstrates the principle.
Direct: https://www.youtube.com/watch?v=wFVITG5Ymnc
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 18th, 2020 at 4:21:12 PM
permalink
Quote: WizardQuote: CrystalMath
1.9780219 miles
Purely numerical solution.
I don't even know where to start, mathematically. I'm sure it would have been no problem when I was in high school, but it makes my head hurt now.I've been wrong before, but I disagree. I worked out a numerical solution in Excel and you can see from the graph below, my answer at least 2.
Ah yes, I was using a height of 6 miles.
2.6373626 miles
I heart Crystal Math.
November 18th, 2020 at 7:15:56 PM
permalink
I was at White Sands from May 1969 through February 1971. The office I was assigned to was the high altitude air defense projects office of the Army Missile Test and Evaluation Directorate.Quote: WizardMy father went to the White Sands Missile Range a lot when I was kid. He had a very high security clearance, so couldn't say much about what he did. However, I do know his expertise was in anti-missile missiles.
I wonder if you two might have met at some point.
During that period, our office worked with contractors for the Nike-Hercules, the SAM-D (which stood for Surface to Air Missile Development and later became the Patriot missile), and the Sprint. While I was there, none of those missiles was fired at a physical target. By the time I left, the Sprint test program was moving to the Kwajalein missile range in the Pacific so that it could be tested against long-range incoming missiles.
I suspect that launches of various missiles at WSMR were used for collection of data for how to detect and track a target missile.
November 19th, 2020 at 7:43:29 PM
permalink
Does anyone request more time, or did I stump the forum?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 21st, 2020 at 4:13:45 PM
permalink
Quote: WizardDoes anyone request more time, or did I stump the forum?
Second and last opportunity to request for more time.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 26th, 2020 at 8:23:28 PM
permalink
So, what's the solution?
November 27th, 2020 at 11:03:50 AM
permalink
Quote: ThatDonGuySo, what's the solution?
I have not gotten around to writing it up. I may make a video of it as writing mathematical notation is time consuming.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
November 27th, 2020 at 7:39:47 PM
permalink
December 7th, 2020 at 9:47:45 PM
permalink
Quote: WizardOkay, I finally wrote it up.
Surface to air missile problem (PDF)
Ok so I'm late to this 1 but I read your comment where you said that the missile to airplane distance wasn't the answer & I was thinking to myself "no duh" but then I thought the distances from the plane's origin above the missile should be the answer & I thought no wait it has to be more complex than that lol. Simple trigonometry could get you this answer :/
Math is the only true form of knowledge
December 7th, 2020 at 10:37:05 PM
permalink
Well played sir. Well played indeed.
Possible typo in spoiler
I think you have a typo that is corrected later, unless I am missing something.
You have (600t-x) on page 3 which I think is correct
On page 4 it changes to (800t-x) and that 800 continues until you reach
line 3 of page 5.
but then line 4 it changes to 0.3sqrt.....which I think is 600/2000......so it is okay from then on
Just all those 800's are 600's on page 4 and (start of) page 5
***nitpicky...but if posting solution.... in the three questions, I would say "How FAR does the missile travel" to match the first question format. As is, the "how LONG does the missile travel?" seems to match the second time question format?
Possible typo in spoiler
I think you have a typo that is corrected later, unless I am missing something.
You have (600t-x) on page 3 which I think is correct
On page 4 it changes to (800t-x) and that 800 continues until you reach
line 3 of page 5.
but then line 4 it changes to 0.3sqrt.....which I think is 600/2000......so it is okay from then on
Just all those 800's are 600's on page 4 and (start of) page 5
***nitpicky...but if posting solution.... in the three questions, I would say "How FAR does the missile travel" to match the first question format. As is, the "how LONG does the missile travel?" seems to match the second time question format?
December 8th, 2020 at 7:47:16 AM
permalink
Quote: chevyWell played sir. Well played indeed.
Thank you!
Quote:Possible typo in spoiler
I think you have a typo that is corrected later, unless I am missing something.
You have (600t-x) on page 3 which I think is correct
On page 4 it changes to (800t-x) and that 800 continues until you reach
line 3 of page 5.
but then line 4 it changes to 0.3sqrt.....which I think is 600/2000......so it is okay from then on
Just all those 800's are 600's on page 4 and (start of) page 5
***nitpicky...but if posting solution.... in the three questions, I would say "How FAR does the missile travel" to match the first question format. As is, the "how LONG does the missile travel?" seems to match the second time question format?
You are absolutely right. Thank you for the correction. I just fixed it.
Last edited by: Wizard on Dec 9, 2020
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 9th, 2020 at 6:17:51 AM
permalink
Wiz,
Three more typos:
Hope this helps!
Dog Hand
Three more typos:
On page 2, "plan" should be "plane".
On page 4, you still have an "800" instead of "600" in the first equation.
Also on page 4, the third equation says:
(8-y)*dx/dy = 600*t - x
When you take the derivative of both sides with respect to y, you get
(8-y)*d²x/dy² + (-1)*dx/dy = 600*dt/dy - dx/dy
You seem to have forgotten the second term on the LHS, which conveniently cancels the second term on the RHS. Thus your "Equation 1" should be
(8-y)*d²x/dy² = 600*dt/dy
This version of Equation 1 agrees with what you used on page 5.
On page 4, you still have an "800" instead of "600" in the first equation.
Also on page 4, the third equation says:
(8-y)*dx/dy = 600*t - x
When you take the derivative of both sides with respect to y, you get
(8-y)*d²x/dy² + (-1)*dx/dy = 600*dt/dy - dx/dy
You seem to have forgotten the second term on the LHS, which conveniently cancels the second term on the RHS. Thus your "Equation 1" should be
(8-y)*d²x/dy² = 600*dt/dy
This version of Equation 1 agrees with what you used on page 5.
Hope this helps!
Dog Hand
