Poll
 | 2 votes (25%) | ||
 | 1 vote (12.5%) | ||
 | 1 vote (12.5%) | ||
 | 2 votes (25%) | ||
 | 1 vote (12.5%) | ||
 | 2 votes (25%) | ||
 | 1 vote (12.5%) | ||
 | 3 votes (37.5%) | ||
 | 2 votes (25%) | ||
 | 1 vote (12.5%) |
8 members have voted
Question: What is the area of a rectangle randomly inscribed in a circle of radius 10?
It may depend on how one randomly inscribes the rectangle. The way I did it was to assume a first corner of the rectangle at a specific location on the circle, say 12:00. Then I randomly chose an adjacent corner on the rectangle anywhere along the circumference of the circle. You can then draw out the rest of the rectangle based on those two points.
I'll make this one beer worthy, but usual rules apply, namely members of the beer club should not post for 24 hours. You may PM me if you can't hold your breath that long. As always, please put answers and solutions in spoiler tags until I call the problem solved.
youtube/UpQsFChVres
Quote: USpapergamesAlso, there is no way to put a corner of the rectangle at 12:00 since that would be the exact middle of the circle and all rectangles must have congruent sides of equal length so the solution Mr. Shackleford is describing would be to solve a trapezoid.
Here is what I meant by putting a corner at 12:00. The second one is at any random point on the circumference. From there, the rest of the rectangle draws itself.
P.S. I just solved for the smallest solution for the problem, check the description of my video for latest update. It's a lot easier to solve a problem when you are already provided with a solution. And taking the problem to the 3rd dimension is much more difficult. Let's see if your form members can solve the problem. Btw, do you think I haven't provided a valid solution to the problem yet?
We have a process for doing math problems here at WoV. Here are the basic rules for problems deemed worthy of their own thread.
1. The one asking gives the audience a chance to answer the problem first. It would ruin the fun if I just told you the answer at the same time I posted the question.
2. The first person with a satisfactory answer AND solution is awarded a beer and are deemed a member of the "beer club."
3. Members of the Beer Club may not post answers or solutions for 24 hours after the a new question is posted, to give new people a chance to join the club. They may ask for clarification on the problem during that 24 hour waiting period.
4. Answers and solutions should be put in spoiler tags, until somebody presents a correct answer and solution.
5. Please don't post links to other sites that go over the same problem.
Choose a random distance d in (0,1) from the origin to side ABCD along the X-axis
The circle containing ABCD has radius sqrt (1 - d2)
Choose a random angle t in (0, PI/2) from the XZ-plane to A
A is at (d, sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
B is at (d, sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
C is at (d, -sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
D is at (d, -sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
E through H are the same as A through D except that the x-value is -d
AB has length 2 sqrt(1 - d2) sin t
AD has length 2 sqrt(1 - d2) cos t
AE has length 2d
The volume is 8 (1 - d2) sin t cos t = 4 (1 - d2) sin 2t
The integral from 0 to PI/2 of 4 (1 - d2) sin 2t dt
= 4 (1 - d2) * the integral from 0 to PI of sin t dt
= 4 (1 - d2) * ((-cos PI) - (-cos 0))
= 8 (1 - d2)
The integral from 0 to 1 of 8 (1 - d2) dd
= 8 - 8 * the integral from 0 to 1 of d2 dd
= 8 - 8 * (13 / 3 - 0)
= 16/3
The mean volume = (16/3) / (1 * PI/2) = 32 / (3 PI)
Quote: Wizard4. Answers and solutions should be put in spoiler tags, until somebody presents a correct answer and solution.
Maybe USpapergames doesn't know how to post spoiler tags?
[spoiler=This is a spoiler tag]Spoiler text goes here[/spoiler]
creates this:
Let ABCD be the rectangle
Note that AC and BD are both diameters of the circle
Choose A arbitrarily, and B uniformly along the circle other than A or with AB being a diameter
Let t be the measure of angle AOB in radians; BOC has measure (PI - t)
Also note that t is a uniform random number in (0, PI)
AB has length 2 (10 sin (t/2))
BC has length 2 (10 sin ((PI - t)/2)) = 2 (10 cos (t/2))
The area of the rectangle = 4 (10 sin (t/2)) (10 cos (t/2))
= 200 (2 sin (t/2) cos (t/2)) = 200 sin t
The integral from 0 to PI of 200 sin t dt = 200 (-cos PI) - (-cos 0))
= 200 (1 - (-1)) = 400
Since t is in (0, PI), the mean area of the rectangle = 400 / PI.
Quote: ThatDonGuyWait a minute...I submitted this after 5:00, but I didn't want to double post, so I edited an earlier post, and it didn't change the posting time.
Let ABCD be the rectangle
Note that AC and BD are both diameters of the circle
Choose A arbitrarily, and B uniformly along the circle other than A or with AB being a diameter
Let t be the measure of angle AOB in radians; BOC has measure (PI - t)
Also note that t is a uniform random number in (0, PI)
AB has length 2 (10 sin (t/2))
BC has length 2 (10 sin ((PI - t)/2)) = 2 (10 cos (t/2))
The area of the rectangle = 4 (10 sin (t/2)) (10 cos (t/2))
= 200 (2 sin (t/2) cos (t/2)) = 200 sin t
The integral from 0 to PI of 200 sin t dt = 200 (-cos PI) - (-cos 0))
= 200 (1 - (-1)) = 400
Since t is in (0, PI), the mean area of the rectangle = 400 / PI.
I deem this correct and a worthy solution! Please add one more beer to the count I owe you. Here is my solution, which I think is simpler.
Let's make the radius 1 and then multiply by 10^2 at the last step to get the answer for a circle of radius 10.
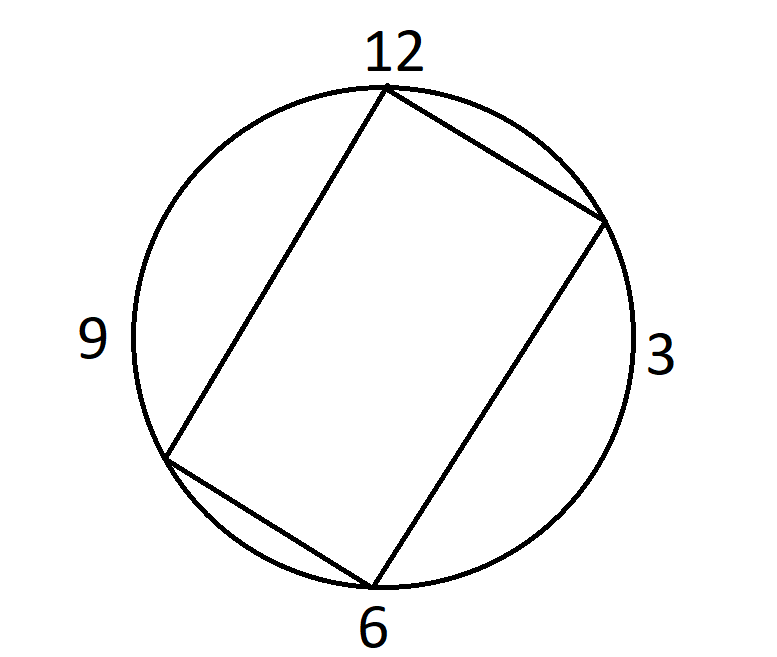
1. Chose an arbitrary point on the circle, for example, the 12:00 position. That will be one corner of the rectangle.
2. Observe that both diagonals of the rectangle will cut through the center of the circle.
3. Another corner of the rectangle will be directly across the first point, at the 6:00 position.
4. Choose a random point anywhere within 90 degrees of the point in step 1, for example anywhere from the 12:00 to 3:00 position. Please note we don't have to go all the way to the 6:00 position, because it doesn't make any difference whether this point is closer to the 12:00 or 6:00 position. This will be the another corner of the rectangle.
5. Call the points from step 1 and 4, A and B. Call the enter of the circle O.
6. Let x be the angle AOB.
7. The area of the rectangle, given x, is 8*(1/2)*sin(x)*cos(x).
8. Integrate that area, 4*sin(x)*cos(x) over the range from 0 to pi/2:
integral of 4*sin(x)*cos(x) dx
Let u = sin(x)
du = cos(x) du
Integral = 4u du
= 2u^2/2
=2*sin^2(x)
9. Plug in the limits of integration of 0 to pi/2 to get 2*(1^2 - 0^2) = 2.
10. Divide that by the range of integration pi/2, to get the average (I admit I forgot this step initially) = 2/(pi/2) = 4/pi.
11. Now, multiply by 10^2 to get the answer for a circle of radius 10: 100*4/pi = 400/pi =127.324.
The equation is X̄A❙◯ = ((R√2+2R)/2 + 2(R−√(R²−(2Rπ÷16)²))) (R√2)/2
Here is the equation broken down X̄A❙◯ = ((B+D)/2 + 2S) B/2
B = Base of Arch
D = Diameter
S = Sagitta
I found the most simplified solution! It's not as small as I would like it but I don't think it can get smaller with fewer characters. Here is the question you should be rewarding the answer to.
X̄A❙◯ = (R²(2√2+12 - √(8+π)(8-π)) √2) / 8
The only reason why my answer is wrong is because the angle on the Sagitta is wrong. Does nobody see the solution as I do? Do you need to use trigonometry or calculus to solve this problem? I don't think so, I think I should be able to solve this problem with just paper & pencil. I think I'm going to just give up now and kill myself, I hate being wrong.
Quote: USpapergamesActually, I messed up. You guys might be right :( I thought I found an elegant solution but no.
The only reason why my answer is wrong is because the angle on the Sagitta is wrong. Does nobody see the solution as I do? Do you need to use trigonometry or calculus to solve this problem? I don't think so, I think I should be able to solve this problem with just paper & pencil. I think I'm going to just give up now and kill myself, I hate being wrong.
Thanks for the new word to me, "sagitta." I had to look it up because our high school trig course didn't teach that. Was sagitta used in your high school trig course?
Nope, I graduated high school sophomore year and went and got my AA at a community college for my junior& senior years.
Quote: ThatDonGuyFor the sphere problem, assuming the volume is desired, and the radius of the sphere is 1,
Choose a random distance d in (0,1) from the origin to side ABCD along the X-axis
The circle containing ABCD has radius sqrt (1 - d2)
Choose a random angle t in (0, PI/2) from the XZ-plane to A
A is at (d, sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
B is at (d, sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
C is at (d, -sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
D is at (d, -sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
E through H are the same as A through D except that the x-value is -d
AB has length 2 sqrt(1 - d2) sin t
AD has length 2 sqrt(1 - d2) cos t
AE has length 2d
The volume is 8 (1 - d2) sin t cos t = 4 (1 - d2) sin 2t
The integral from 0 to PI/2 of 4 (1 - d2) sin 2t dt
= 4 (1 - d2) * the integral from 0 to PI of sin t dt
= 4 (1 - d2) * ((-cos PI) - (-cos 0))
= 8 (1 - d2)
The integral from 0 to 1 of 8 (1 - d2) dd
= 8 - 8 * the integral from 0 to 1 of d2 dd
= 8 - 8 * (13 / 3 - 0)
= 16/3
The mean volume = (16/3) / (1 * PI/2) = 32 / (3 PI)
Maybe USpapergames doesn't know how to post spoiler tags?
[spoiler=This is a spoiler tag]Spoiler text goes here[/spoiler]
creates this:Spoiler text goes here
Your solution makes no sense and is way off from my answer! If the radius of the sphere is 1 then the sphere volume is = 4.19 and the maximum cube inscribed in a sphere is 1.54 your answer is larger than the largest volume of a rectangular prism inscribed in a sphere with the radius = 1. Your answer 32÷3π = 3.4 can't possibly be the correct answer.
Quote: WizardQuote: ThatDonGuyWait a minute...I submitted this after 5:00, but I didn't want to double post, so I edited an earlier post, and it didn't change the posting time.
Let ABCD be the rectangle
Note that AC and BD are both diameters of the circle
Choose A arbitrarily, and B uniformly along the circle other than A or with AB being a diameter
Let t be the measure of angle AOB in radians; BOC has measure (PI - t)
Also note that t is a uniform random number in (0, PI)
AB has length 2 (10 sin (t/2))
BC has length 2 (10 sin ((PI - t)/2)) = 2 (10 cos (t/2))
The area of the rectangle = 4 (10 sin (t/2)) (10 cos (t/2))
= 200 (2 sin (t/2) cos (t/2)) = 200 sin t
The integral from 0 to PI of 200 sin t dt = 200 (-cos PI) - (-cos 0))
= 200 (1 - (-1)) = 400
Since t is in (0, PI), the mean area of the rectangle = 400 / PI.
I deem this correct and a worthy solution! Please add one more beer to the count I owe you. Here is my solution, which I think is simpler.
[spoiler=Wiz solution]
Let's make the radius 1 and then multiply by 10^2 at the last step to get the answer for a circle of radius 10.
1. Chose an arbitrary point on the circle, for example, the 12:00 position. That will be one corner of the rectangle.
2. Observe that both diagonals of the rectangle will cut through the center of the circle.
3. Another corner of the rectangle will be directly across the first point, at the 6:00 position.
4. Choose a random point anywhere within 90 degrees of the point in step 1, for example anywhere from the 12:00 to 3:00 position. Please note we don't have to go all the way to the 6:00 position, because it doesn't make any difference whether this point is closer to the 12:00 or 6:00 position. This will be the another corner of the rectangle.
5. Call the points from step 1 and 4, A and B. Call the enter of the circle O.
6. Let x be the angle AOB.
7. The area of the rectangle, given x, is 8*(1/2)*sin(x)*cos(x).
8. Integrate that area, 4*sin(x)*cos(x) over the range from 0 to pi/2:
integral of 4*sin(x)*cos(x) dx
Let u = sin(x)
du = cos(x) du
Integral = 4u du
= 2u^2/2
=2*sin^2(x)
9. Plug in the limits of integration of 0 to pi/2 to get 2*(1^2 - 0^2) = 2.
10. Divide that by the range of integration pi/2, to get the average (I admit I forgot this step initially) = 2/(pi/2) = 4/pi.
11. Now, multiply by 10^2 to get the answer for a circle of radius 10: 100*4/pi = 400/pi =127.324.
[spoiler=Wiz solution]
I truly think my way of solving this problem is the best way, it's a geometry problem not a trigonometry problem so use the tools of geometric principals. I think the degree of the sagitta affects the heights which would cause my equation to be slightly off :(
Quote: USpapergamesI think I just suck at geometry then. I don't know why I didn't see the angle of the sagitta being as not being a factor :(
I had to look up the Sagitta. I don't see how that would help you. This is a very textbook integral calculus problem.
Quote: USpapergamesQuote: ThatDonGuyFor the sphere problem, assuming the volume is desired, and the radius of the sphere is 1,
Choose a random distance d in (0,1) from the origin to side ABCD along the X-axis
The circle containing ABCD has radius sqrt (1 - d2)
Choose a random angle t in (0, PI/2) from the XZ-plane to A
A is at (d, sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
B is at (d, sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
C is at (d, -sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
D is at (d, -sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
E through H are the same as A through D except that the x-value is -d
AB has length 2 sqrt(1 - d2) sin t
AD has length 2 sqrt(1 - d2) cos t
AE has length 2d
The volume is 8 (1 - d2) sin t cos t = 4 (1 - d2) sin 2t
The integral from 0 to PI/2 of 4 (1 - d2) sin 2t dt
= 4 (1 - d2) * the integral from 0 to PI of sin t dt
= 4 (1 - d2) * ((-cos PI) - (-cos 0))
= 8 (1 - d2)
The integral from 0 to 1 of 8 (1 - d2) dd
= 8 - 8 * the integral from 0 to 1 of d2 dd
= 8 - 8 * (13 / 3 - 0)
= 16/3
The mean volume = (16/3) / (1 * PI/2) = 32 / (3 PI)
Maybe USpapergames doesn't know how to post spoiler tags?
[spoiler=This is a spoiler tag]Spoiler text goes here[/spoiler]
creates this:Spoiler text goes here
Your solution makes no sense and is way off from my answer! If the radius of the sphere is 1 then the sphere volume is = 4.19 and the maximum cube inscribed in a sphere is 1.54 your answer is larger than the largest volume of a rectangular prism inscribed in a sphere with the radius = 1. Your answer 32÷3π = 3.4 can't possibly be the correct answer.
Choose a random distance d in (0,1) from the origin to side ABCD along the X-axis
The circle containing ABCD has radius sqrt (1 - d2)
Choose a random angle t in (0, PI/2) from the XZ-plane to A
A is at (d, sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
B is at (d, sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
C is at (d, -sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
D is at (d, -sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
E through H are the same as A through D except that the x-value is -d
AB has length 2 sqrt(1 - d2) sin t
AD has length 2 sqrt(1 - d2) cos t
AE has length 2d (not 2 - otherwise the prism doesn't fit in the sphere, now does it?)
The volume is 8d (1 - d2) sin t cos t
The integral from 0 to PI/2 of 8d (1 - d2) sin t cos t dt
= the integral from 0 to PI/2 of 8d (1 - d2) sin t d (sin t)
= the integral from 0 to 1 of 8d (1 - d2) x dx
= 8d (1 - d2)
The integral from 0 to 1 of 8x (1 - x2) dx
= 8 * the integral from 0 to 1 of (x - x3) dx
= 8 * ((12/2 - 14/4) - 0)
= 8 * 1/4 = 2
The mean volume = 2 / (PI/2 * 1) = 4 / PI
Choose a random distance d in (0,1) from the origin to side ABCD along the X-axis
The circle containing ABCD has radius sqrt (1 - d2)
Choose a random angle t in (0, PI/2) from the XZ-plane to A
A is at (d, sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
B is at (d, sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
C is at (d, -sqrt(1 - d2) cos t, -sqrt(1 - d2) sin t)
D is at (d, -sqrt(1 - d2) cos t, sqrt(1 - d2) sin t)
E through H are the same as A through D except that the x-value is -d
AB has length 2 sqrt(1 - d2) sin t
AD has length 2 sqrt(1 - d2) cos t
AE has length 2d (not 2 - otherwise the prism doesn't fit in the sphere, now does it?)
The volume is 8d (1 - d2) sin t cos t
The integral from 0 to PI/2 of 8d (1 - d2) sin t cos t dt
= the integral from 0 to PI/2 of 8d (1 - d2) sin t d (sin t)
= the integral from 0 to 1 of 8d (1 - d2) x dx
= 8d (1 - d2)
The integral from 0 to 1 of 8x (1 - x2) dx
= 8 * the integral from 0 to 1 of (x - x3) dx
= 8 * ((12/2 - 14/4) - 0)
= 8 * 1/4 = 2
The mean volume = 2 / (PI/2 * 1) = 4 / PI
This is a lot better work & makes more sense how you derived the answer!!! Very good, the problem is my equation for the volume of the rectangular prism is off since my equation for the rectangle inside of a circle is wrong :( I double-checked your work on 2D area & your equation is wrong! 400/π might be the right answer but the actual equation for the average area of the rectangle inscribed in a circle is actually 4R²/π! I like how you guys can give me the answer but not the equation lol. So 4R/π as the solution doesn't exactly make a whole lot of sense as the solution for the volume in 3D. Keep working on it, I think you're close!
Wizard
I had to look up the Sagitta. I don't see how that would help you. This is a very textbook integral calculus problem.
I understand how to solve this using calculus but I purposely wanted to avoid that by using a more elegant solution from geometric principles. The fact that you don't see how the sagitta would help solve the problem just tells me you guys are just good and making calculations & not just sticking to math tricks that can be done without the need of a calculator. I am going to make another video of this problem and explain how I would solve this problem using nothing but pen/paper & my mind. It can be done sir, I know it can!
I did a simulation doing the following:
Each vertex of the prism can be expressed as (+/- x, +/- y, +/- z), where x, y, and z are positive, and x^2 + y^2 + z^2 = 1
Select a random number x in (0, 1)
Select a random number y in (0, 1 - sqrt(1 - x^2))
z = sqrt(1 - x^2 - y^2)
Since four parallel edges go from -x to +x, four from -y to +y, and four from -z to +z, the volume = (2x) (2y) (2z) = 8xyz.
However, when I do this, I get a mean volume of 2/3.
Quote: ThatDonGuyI am not as confident of my answer as I was...
I did a simulation doing the following:
Each vertex of the prism can be expressed as (+/- x, +/- y, +/- z), where x, y, and z are positive, and x^2 + y^2 + z^2 = 1
Select a random number x in (0, 1)
Select a random number y in (0, 1 - sqrt(1 - x^2))
z = sqrt(1 - x^2 - y^2)
Since four parallel edges go from -x to +x, four from -y to +y, and four from -z to +z, the volume = (2x) (2y) (2z) = 8xyz.
However, when I do this, I get a mean volume of 2/3.
I see your problem. So here is how you do the solution using calculus. You want an inverse relationship between -X³, +Y³, -Z³ so that when you take the edge value of the maximum volume of a cube inscribed in a sphere and then divide the width & depth values by 2 the height value will increase in value. Without this relationship defined your calculations will never be correct. This is why I like working with equations so that why I can always test your solution ;) I like how you're also unsure of your work. I'm sorry I don't have a lot of time to spend this. I wanted to do another video but instead, I ended up writing a draft of a business contract :/
So I think the solution would need the starting coordinates to be the corners of the cube with the maximum volume inscribed in a sphere and use the equation X̄A❙³◯³ = (X²Z²)/4 (2S+Y²). Just remember that the sagitta is at an angle and needs to be rotated to the Y³ angle. The difference in length when rotated is 58% of the Sagitta.
Quote: ThatDonGuyI am not as confident of my answer as I was...
I did a simulation doing the following:
Each vertex of the prism can be expressed as (+/- x, +/- y, +/- z), where x, y, and z are positive, and x^2 + y^2 + z^2 = 1
Select a random number x in (0, 1)
Select a random number y in (0, 1 - sqrt(1 - x^2))
z = sqrt(1 - x^2 - y^2)
Since four parallel edges go from -x to +x, four from -y to +y, and four from -z to +z, the volume = (2x) (2y) (2z) = 8xyz.
However, when I do this, I get a mean volume of 2/3.
I am not entirely sure these points are uniformly random.
Using this method to select a random point on the sphere:
(a) Choose a random angle t in (0, 2 PI)
(b) Choose a random number x in (0,1), and set angle p = arccos(2x-1)
(c) The coordinates of one of the vertices is (sin t cos p, cos t cos p, sin p)
(d) The volume = 8 sin t cos t sin p cos^2 p
This gives me a mean volume of 1/2...
Quote: ThatDonGuyI am not entirely sure these points are uniformly random.
Using this method to select a random point on the sphere:
(a) Choose a random angle t in (0, 2 PI)
(b) Choose a random number x in (0,1), and set angle p = arccos(2x-1)
(c) The coordinates of one of the vertices is (sin t cos p, cos t cos p, sin p)
(d) The volume = 8 sin t cos t sin p cos^2 p
This gives me a mean volume of 1/2...
There is no need for random points. Your brute force method is just not the right approach to solving this. I think this is a mathematical flaw within your reasoning. There actually is a rectangular prism that has the exact same volume as the average of all rectangular prisms inscribed within a sphere. I gave you the exact points & how to solve for this rectangular prism. Please review my last reply over again. The process in which you would calculate the average by actually recreating all the possible coordinates is nuts ;)
Quote: USpapergamesThere is no need for random points. Your brute force method is just not the right approach to solving this. I think this is a mathematical flaw within your reasoning. There actually is a rectangular prism that has the exact same volume as the average of all rectangular prisms inscribed within a sphere. I gave you the exact points & how to solve for this rectangular prism. Please review my last reply over again. The process in which you would calculate the average by actually recreating all the possible coordinates is nuts ;)
I find it amusing to hear integration referred to as brute force.
With a radius = 10
Maximum Cube inscribed (All figures rounded to nearest thousandth:
Side = 1.155
Face Diagonal = 1.633
Space Diagonal = 2
Face Area = 94.28
Surface Area = 800
Volume = 1,539.601
Sagittal Arch (at an angle) = (5π/8)×58.21144
So here is the equation. (Face Area / 4) × (Side + 2 × Sagitta)
The area without the additional length of the Sagitta = 371.793 ft³ so we know it can't be less than that & is very close to the answer. Let me find some free time tonight & I'll solve the Sagitta problem & we will have the answer. Got to get back to work now :/
Quote: unJonI find it amusing to hear integration referred to as brute force.
Honestly, I was referring to using a software program to run all the possible sizes of the rectangular prism and divide by the sample size as brute force. It's easy to find the answer using a program and then use calculus to describe it later.
Here is the solution:
Start by graphing the equation x²+y²=10²
Then draw a line from equation x+y=5 & x+y=-5
The area in between both lines is the answer
5²+5²=10² × the length of both points of either line that contacts the circumference.
7.071 × 18.707 = 132.277
Does that answer look familiar? It does to me because that is the 1st & only answer I have ever given for this problem! Prove my work wrong 🙏
Quote: USpapergamesYou guys don't realize there is a difference between the average of all the different areas of a rectangle vs the average way a rectangle can be drawn. The rectangle only has 1/16 of the circumference of the circle to be drawn in, so 1/32 of the circle is your median answer since there is no mean randomly drawing inscribed rectangles. Tho I do like the idea of a mean of all potential areas but that is definitely a calculus problem. The hard part was calculating the length of the rectangle, not easy ;)
But your question was the average area of a random rectangle inscribed in a circle. So we need to know the distribution of all rectangles that can be so inscribed so the average of all those triangles can be taken.
Quote: unJonBut your question was the average area of a random rectangle inscribed in a circle. So we need to know the distribution of all rectangles that can be so inscribed so the average of all those triangles can be taken.
Think about the question a little harder. A rectangle can only be drawn so many different ways and the average of that must be halfway between all the sizes of the rectangle, not the area! It's obvious you guys aren't that good at word problems. The question says the average area of a rectangle, not all rectangles. Meaning this must be the average rectangle & then find it's area! No wonder nothing you guys were doing made any sense to me!
Shackleford's Question: What is the area of a rectangle randomly inscribed in a circle of radius 10?
Again, the rectangle is singular, not plural! Again, everyone is wrong except me, I win🏆. Equations don't lie just like computer simulations! But misinterpretation happens all the time in mathematics, I'm just surprised Shackleford could misinterpret the question even though he clearly posted the right wording of the question. This just goes to show you how easy it is to assume a question that you have solved previously many times. I really did think it had to be the wording of the question for everyone to misinterpret the answer :/
P.S. Try to use nothing but pen, paper & a basic calculator, your reliance on technology has stunted your equation skills. Bonus points for whoever gives me the equation & not just an explanation of how they got the correct answer ;)
Quote: USpapergamesLiterally, everyone is wrong except me because nobody spent any time trying to comprehend the question lol. They all thought it was a mean of all averages problem because they have seen so many similar calculus problems even though I'm shouting up & down that it's not a calculus problem & no trig required but everyone is just ignoring me as if I'm crazy instead of just asking for more information if nothing I was saying made any sense to you. After teaching high school math for 6 years I've learned the worst students are often the brightest but refuse to ask questions for fear of looking stupid.
Or maybe it's because nobody except you seems to have any idea what the definition of an "average rectangular prism" is. Average as defined in what way?


