Poll
| No votes (0%) | |||
 | 2 votes (28.57%) | ||
 | 2 votes (28.57%) | ||
| No votes (0%) | |||
 | 2 votes (28.57%) | ||
 | 2 votes (28.57%) | ||
 | 2 votes (28.57%) | ||
 | 1 vote (14.28%) | ||
 | 1 vote (14.28%) | ||
 | 3 votes (42.85%) |
7 members have voted
Quote: 538.comYouíre walking along the middle of a wide sidewalk when you see someone walking toward you from the other direction, also down the middle of the sidewalk, 12 feet away. Being responsible citizens, you pass each other while maintaining a distance of at least 6 feet at all times. By the time you reach each otherís original positions, you should be back in the middle of the sidewalk again.
You should assume that the other person follows the same path you do, but flipped around (since theyíre walking in the opposite direction). For example, you could both walk 3 feet to the left, 12 feet forward and finally 3 feet back to the right, walking a total of 18 feet before swapping positions.
Being lazy (I mean, efficient), youíd like to know the shortest distance you and the other person could walk so that you can switch positions, all while staying at least 6 feet apart at all times. What is this distance?
Extra credit: Now suppose the person walking toward you has no intention of straying from the center of the sidewalk (sigh), and itís entirely up to you to maintain a distance of at least 6 feet. In this case, what is the shortest distance you would have to walk to reach the other personís original position?
538 doesn't mention the speed of the walkers, but for purposes of discussion here, let's assume both walk at the same speed.
So far, I have an answer to part 1 only. I'll put my answer in spoiler tags below.
I think this problem is too hard for the "easy puzzle" thread. However, I'm going to not apply the usual beer club rules. We're all in the same boat on this one.
Pi + 6 * (square root of 3), or about 13.53 feet.
The problem with #2 is, it's a "moving target."
My first thought was, find the distance d that the other person will walk so you will be on the tangent of the 6-foot circle with the other person as the center when you also walk distance d - but you can't then simply "walk around the circle" as the circle is moving.
(45)^.5 * 2 = 13.416 feet . Which is wrong
If you have to go the same speed then you could aim for a point 6' away from the path. At the same time the other person walks along the path. It transpires (think 3-4-5 triangle) if the other person walks 7.5', you can walk (4.5^2+6^6)=7.5'. However the issue is whether the two of you ever get closer than 6' (which you do!). Shame really as it was nice to have a 3-4-5 triangle in it.
My feeling is you aim along a line then an arc of some kind to a point 6' from the path. While you do that, the other person has got beyond the half way point, so the answer isn't symetrical. Also as the other person will have done your distance, this is greater than 6' are also the sum of a line and the length of an arc.
I've been thinking about the second part for a couple hours now. It is going to be tricky.
Let's say the horizontal movement is straight ahead along the sidewalk, as if the other guy wasn't there.
I think you will start out walking in either direction 60 degrees away from straight ahead. After walking 6 feet, you'll be 6 feet away from the rude guy walking straight ahead.
Then it gets tricky. I think you'll take some kind of an altered cycloid path -- getting pushed back horizontally and up vertically. I think at some point you'll be 6 feet vertically from the straight walker. Then continue on this curved path a little until you can leave it along its tangent line and head straight to the point 12 feet directly ahead of where you started.
I think this is going to involve parametric equations and arc length. Here is where the air starts to get thin for me.
I tend to think I won't be the first to solve this one, knowing the brain power here. Whoever solves it first, please give a good solution.
p.s. Choice 8 in the poll should have read, "I hope the quarantine is over by April 8 2024.
But I think you should mentioned that both person walk with same speed ? Am I missing something ?
For part 2, Assuming both walk with same speed, it involve arc length, min distance = 18.1633 . . .should be very close but not 100% accurate. LOL
My initial ideas, not fully proved, get an upper bound of about 18.125 using the following logic.Quote: ssho88...For part 2, Assuming both walk with same speed, it involve arc length, min distance = 18.1633 . . .should be very close but not 100% accurate. LOL
The Walker goes from A to B along the blue path.
You follow the red dots and at some stage have to cross 6 feet apart (shown by the right hand gold line).

Part 1: PQ PQC is an equilateral triangle. If you go to point Q, then you will have walked 6 feet and then be 6 feet from the Walker.
Part 2 : QR If you continue on that path to R, then you're going outside what you have to (Note: I haven't proved this so am happy to be corrected, in which case it's likely to be similar to the 18.163 above.)
Part 3 : RS Once you're on the six foot path, go along it until you're at the same height as the Walker (D S).
In theory I think you follow an arc (the blue one is an elipse with radii 3 and 6). Also you should have aimed for a point to meet it at right angles, therefore Q might be further up.
Parts 4 and 5 are nearly symettric since you start out by following the same path as in part 3 and part 2. (In theory you follow the arc in identical manner until you're travelling at right angles to the walker...
Part 6 : UV ...then head straight home.
Each part has a number, typically involving square roots (e.g. UV = SQRT(75) ), but as this is all an approximation.
I think the puzzle involves somehow proving an elipse is the path needed and by weird magic working out where the perpendiculars meet the curve.
Quote: charliepatrickMy initial ideas, not fully proved, get an upper bound of about 18.125 using the following logic.
The Walker goes from A to B along the blue path.
You follow the red dots and at some stage have to cross 6 feet apart (shown by the right hand gold line).
Part 1: PQ PQC is an equilateral triangle. If you go to point Q, then you will have walked 6 feet and then be 6 feet from the Walker.
Part 2 : QR If you continue on that path to R, then you're going outside what you have to (Note: I haven't proved this so am happy to be corrected, in which case it's likely to be similar to the 18.163 above.)
Part 3 : RS Once you're on the six foot path, go along it until you're at the same height as the Walker (D S).
In theory I think you follow an arc (the blue one is an elipse with radii 3 and 6). Also you should have aimed for a point to meet it at right angles, therefore Q might be further up.
Parts 4 and 5 are nearly symettric since you start out by following the same path as in part 3 and part 2. (In theory you follow the arc in identical manner until you're travelling at right angles to the walker...
Part 6 : UV ...then head straight home.
Each part has a number, typically involving square roots (e.g. UV = SQRT(75) ), but as this is all an approximation.
I think the puzzle involves somehow proving an elipse is the path needed and by weird magic working out where the perpendiculars meet the curve.
Similar idea ! I use 3 known points to form quadratic equation . . .then use integration to calculate the arc length . . .BUT STILL AN ESTIMATION.
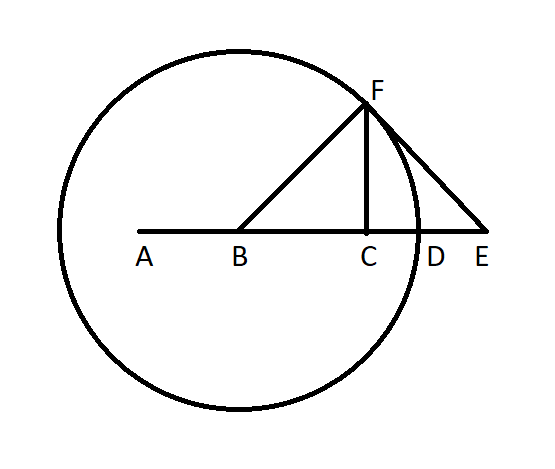
Suppose the selfish walker starts at pt A = (0,0) and walks right along the X axis. Thus, the unselfish walker starts at point E = (12,0).
The circle in this diagram is the 6-ft. radius of safety.
I submit that the unselfish walker should aim for a point to be soon on the tangent of this circle.
When the selfish walker reaches point B, the unselfish walker should reach the tangent of the circle. In other words, AB = EF
Here are some things we know:
- Angle BFE is 90 degrees, because the unselfish walker walked straight to the tangent point.
- BF = 6, because B is the center of the circle and F is along the circle's edge.
- BE = 12 - EF, because AE = 12, AB + BE = AE, and AB = EF
From the Pythagorean forumula:
BF^2 + EF^2 = BE^2
6^2 + EF^2 = (12 - EF)^2
36 + EF^2 = 144 - 24EF + EF^2
24EF = 108
EF = 9/2 = 4.5
There are two ways to measure the area of triangle BEF. One is half the square of sides length BF and EF. That would be (1/2) * 6 * 4.5 = 13.5
The other is (1/2) * base * height.
We have established that EF = 9/2, and AF = EF, so AB = 9/2. Thus BE = 12 - AB = 15/2.
The formula for the area that way is (1/2) * CF * 15/2 = (15/4) * CF.
Equating the two formulas for the area of triangle BEF:
13.5 = (15/4) * CF
CF = 13.5 * (4/15) = 18/5 = 3.6.
Using more simple applications of Pythagorean, we find:
AB = 4.5
BC = 4.8
CE = 2.7
So, when the unselfish walker reaches the circle of danger of the selfish walker, he will be at point (9.3,3.6).
Part 2, will be much harder. I assume the unselfish walker will walk along the circle as it moves right along the x axis. Here is where we'll need some calculus.
I think this square wheel video will come in handy.

Never budge! That's my rule. Never budge in the least!
Not an inch to the west! Not an inch to the east!
Quote: GialmereI actually came across this problem when I was a kid except both walkers were selfish. The solution was...
...to build civilization around them.
Never budge! That's my rule. Never budge in the least!
Not an inch to the west! Not an inch to the east!
I've seriously wondered what happens when this happens, no joking aside. It happens a lot that two men are headed straight towards each other and one will absolutely not veer out of the way, even a little. When this happens, I'll take the moral high ground and get out of the "selfish walker"'s way. However, I'd like to see what happens when two of them have a face off.
Quote: WizardSo, when the unselfish walker reaches the circle of danger of the selfish walker, he will be at point (9.3,3.6).
After some calculus, which I'll explain later, I show that when the selfish walker reaches his destination (12,0), the unselfish walker will have been pushed back 4.5 units, and risen sqrt(15.75)-3.6 = 0.3686 units to y = sqrt(15.75) =~ apx. 3.9686. In other words, he will be at point (13.8, sqrt(15.75)). This is 14.3593 directly away from the destination. Considering he must go up further to get around the danger circle, it will take much longer.
He could have just gone 6 units up the Y axis to start with and have been in better shape.
So, I think my whole strategy is flawed. As I think about it, he is mainly walking ahead to just get pushed back.
Sorry to have wasted your time.
Not sure I read these links correctly but, if a smoke particle is twice the size of a Covid 19 particle, would it be reasonable to assume that when in a room, if you can smell cigarette smoke [or see it] that were the smoker carrying the virus and you can smell the smoke, you have a good chance of inhaling the virus along with the secondhand smoke?
Anyway, that's how I see secondhand smoke, as carrying a plague.
https://smartairfilters.com/en/blog/coronavirus-pollution-masks-n95-surgical-mask/
https://www.ncbi.nlm.nih.gov/pubmed/2751166
I think these links indicate a Covid particle is about 1/2 the size of a smoke particle.
My reason for even posting this is, we all know how far smoke travels in a room, I consider that the virus travels at least half as far as smoke. I think that droplets of virus on the floor can re aerosol from being stomped on, so they get around further than 6 ft?
Ever come home from hours in a Vegas casino, or a few hours in a smoke filled bar, toss your clothes in a pile and shower, just to come out of the shower and smell the stinky pile? Think of the stink as virus, take off your outside clothes and put them in the washing machine.
First time I ever saw a laundry [washer and dryer] in a bathroom was at my girlfriends [wife] apartment. It made so much sense to me, to disrobe in the shower room, toss dirty clothes in the machine, instead of having a laundry basket and saving them up for laundry time. Step out of the shower and press, wash. Easy peesy.
Quote: Wizard...
Let's say the horizontal movement is straight ahead along the sidewalk, as if the other guy wasn't there.
I think you will start out walking in either direction 60 degrees away from straight ahead. After walking 6 feet, you'll be 6 feet away from the rude guy walking straight ahead.
Then it gets tricky. I think you'll take some kind of an altered cycloid path -- getting pushed back horizontally and up vertically. I think at some point you'll be 6 feet vertically from the straight walker. Then continue on this curved path a little until you can leave it along its tangent line and head straight to the point 12 feet directly ahead of where you started.
I think this is going to involve parametric equations and arc length. Here is where the air starts to get thin for me.
I tend to think I won't be the first to solve this one, knowing the brain power here. Whoever solves it first, please give a good solution.
Using your idea of walking in a direction 60 degrees from straight ahead for six feet, then keeping a constant 6 feet from the straight walker, and then leaving this curved path straight to the destination, I get a total distance of 17.4469 feet.
I used the following numerical method. I considered a moving 6-foot-radius circle centered on the straight walker, and a circle of radius 1/1000 foot about the curved-path walker. One of the intersections of the two circles gives the next approximate location of the curved-path walker. Finding the slope of the segment between two adjacent points and comparing it to the slope of the line from the path to the destination tells when to end the curved path.
The total path of this method gives 6 feet for the initial straight path + 2.7240 feet for the curved path + 8.7229 feet for the final tangent walk for a total of 17.4469 feet.
The above method assumes both people walk at the same speed as each other. (They can both speed up or slow down, but they must do it simultaneously.) However, if the 2nd walker is allowed to pause while the other continues walking, he can do the initial 60-degree walk but all the way to 6 feet from the center line and pause, letting the other guy pass. Then he can walk straight to the destination. This total walk would be only 17.3619 feet.
And if the 2nd guy is allowed to run, he can run to the point (6,6), let the 1st guy pass, and then walk to his destination for a total of 16.9706 feet.
I guess a calculus method can be derived from the numerical method, but I'm stuck.

1. Both walk 3.3981 feet. The unselfish walker will walk at such an angle he touches the danger circle after the 3.3981 seconds.
2. The unselfish walker will walk at an angle twice that of the tangent line to the direction of travel of the selfish walker. The reason for doubling the angle is to keep from entering the danger circle, as it is approaching you. The unselfish walker will do this until he reaches the top of that circle. Using the coordinate system I explained before, the unselfish walker will be at point (11.55007666,6) at this time.
3. The short walker will walk along the back side of the danger circle a very short time, until his direction would take him directly to point (0,0), at which point he will do that.
I have not fussed with the "very short time" part of the puzzle and had the unselfish walker walk straight back when he got to the top of the circle. Total time spent is 21.5344.
I hate to question Charlie, but the curved part of your graph doesn't seem to reflect that the selfish walker is moving towards you. I think the part from Q to S should be steeper and from S to U more flat.
Please do as my assumptions may be false.Quote: Wizard...I hate to question Charlie, but the curved part of your graph doesn't seem to reflect that the selfish walker is moving towards you. I think the part from Q to S should be steeper and from S to U more flat.
I started where you (the Walker) were on the six foot path opposite the selfish one (the Person) (DS) and then worked out how you could gradually move, getting nearer to the path but maintaining the six foot distance.
In the first case the Person continues Northbound (in my diagram upwards from D) while you head Southbound (down from S). As the Person moves a distance (say .001) North, the curve you take will have length of .001, ideally maintain six feet apart at all times (my estimate actually ensured you used a straight line at right angles to where the Person was, so it gradually got further away but then occasionally made a correction to back back closer), and move you towards the path.
If the curve thus drawn keeps you at six foot away (or as near as makes no difference) while the person walks North, then by reflected symmetry the same curve (reflected) will work as the person is still walking towards D and you are have yet to reach S.
The only difference is when you join/leave the curve as your distance from the start will be shorter than your distance to the finish. This is why you join the curve earlier, and leave it sooner, as the straight lines PQ is steeper (or makes less progress South) than the UV line.
A few interesting ideas might come from looking at a "tractix" ( https://en.wikipedia.org/wiki/Tractrix ), the problem I see is the distance covered by the puller is much greater than the end of the pole.
There's also a list of curves at https://www.matematica.pt/en/useful/list-curves.php and the concept of an involute. Cycloid looked interesting, take a point on a circle and roll the circle along a straight line, look at how the point moves. Then consider extending the diameter 2r. The problem is the cicrcle moves 2 Pi r whears the point moves 4r.
I think the trick is to try and find which curve it is!
Edit: Just found this - might this be an idea!

dy/dt = 1 - (y + t -12)2/18
(dx/dt)2 + (dy/dt)2 = 1
with dx/dt>0 before x reaches 6, and dx/dt < 0 afterwards.
x(6) = 3*sqrt(3)
y(6)=3
?
(Edit: I corrected the initial conditions' time.)
Even a numerical solution would be nice.
I believe the solution is the curved part of the path to avoid the selfish walker.
This solution assumes the two walkers must maintain the same constant speed. I set my unit of time to make the speed 1 foot / unit.
I couldn't solve the above differential equation, but typing y' = 1 - (y+t-12)^2/18; y(6)=3 into WolframAlpha gives a nice solution for y.
Then x = sqrt[36 - (y + t - 12)^2 ] to keep the distance to the selfish walker 6 feet.
x' = - sqrt( 1 - (y')^2 ) for after x becomes 6. Next, dy/dx = y' / x' which we set equal to the slope of the line to the destination, (12 - y) / (0 - x).
Trial and error gives t = 8.723448, x = 5.634036, and y = 5.339957.
The length of the straight line between (x, y) and (0, 12) is sqrt( (12-y)^2 + (0-x)^2 ) = 8.723448, which happens to equal the time for the sum of the initial straight path and the curved path!
So, the total distance is 17.446895 feet.
Answers to this puzzle are now posted. Along with new puzzles. ChesterDog appears to have the right solution (at least numerically, didn't check the formulae).
Quote: rsactuaryIt's surprising to me that the path isn't symmetric, along the lines of what was proposed in this thread. I never would have thought outside of that box.
May I know what is the exact angle between the INITIAL RED STRAIGHT PATH and the horizontal BLUE line ? Not exact 60 dgeree ?
Starting at coordinates (0,12), the selfish walker's path is described by x=0 and y=12 - t, assuming his speed is 1 foot/unit time.
A 6-foot circle around him would be x2+ (y - 12 + t)2 = 36 (Eqn. 1).
The other walker's trajectory is counterclockwise about this circle, with a speed of 1. His speed squared can be expressed as: xt2 + yt2 = 1 (Eqn. 2).
Differentiating the path with respect to t gives: 2xxt + 2(y-12+t)(yt+1) = 0. And solving for xt gives: xt = (12-y-t)(yt+1)/x (Eqn. 3).
Equations 1, 2, and 3 can be combined to eliminate x and xt to give:
18 yt2 + (y-12+t)2yt -18 + (y-12+t)2 = 0
This can be solved for yt using the quadratic formula (using the + instead of the -) to give:
yt = 1 - (y+t-12)2/18.
And the initial condition is y(6) = 3.
Quote: ssho88ChesterDog, is the angle between initial red straight path and horizontal blue line EXACT 60 degree ?
Yes--it's exactly 60 degrees.
A good way to prove that is this: If the selfish walker starts at B (0,12), then if he would walk for 6 feet, he would be at O (0,6). Imagine a 6-foot-radius circle centered at O (0,6).
If the other person started at A (0,0) walking 60 degrees from straight ahead, he would touch that circle at C, 6 feet from his starting point. And he would arrive at the circle at the same time the selfish walker reached (0,6).
In other words, both walkers went 6 feet to be 6 feet away from each other. Think of the circle O with an equilateral triangle AOC having the circle's radius AO as its base.
Edit: Now, I see that the above doesn't prove that the minimum total distance is achieved by starting at 60 degrees.


