Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted

If the true answer was 0%: that you couldn't guess correctly, then this would be untrue since there is a 1 in 4 chance of picking 0%.
If the true answer was 25%, then this would be untrue since there is a 2 in 4 chance of picking 25%.
If the true answer was 50%, then this woul;d be untrue since there is a 1 in 4 chance of picking 50%.
Thus you must pick the answers with different probabilities. So picking 25% with 25% chance and (say) 0% with 75% chance would give a correct answer. Similarly for 50% with 50% chance provided 0% can be picked with some probability. I suspect you can have two correct answers if (say) 50% was 50% and 25% was 25%, but I'm not sure!
Thus in Mathematics terms, we don't have enough information to state a definitive answer.
A warden approaches a prisoner, who also happens to be a logician, and says, "If the next statement out of your mouth is true, I will kill you by hanging. If the next statement out of your mouth is false, I will kill you by firing squad."
What should the prisoner say?
Quote: WizardA warden approaches a prisoner, who also happens to be a logician, and says, "If the next statement out of your mouth is true, I will kill you by hanging. If the next statement out of your mouth is false, I will kill you by firing squad."
link to original post
What should the prisoner say?
"You will kill me by firing squad."
If he is killed by firing squad, his last statement was true, so he should have been hanged.
If he is hanged, his last statement was false, so he should have been killed by firing squad.
The problem is, if he is freed, "the next statement out of his mouth" was false, so he should have been killed by firing squad. No matter what happens, the warden's statement is false.
The warden then killed the prisoner by electric chair.
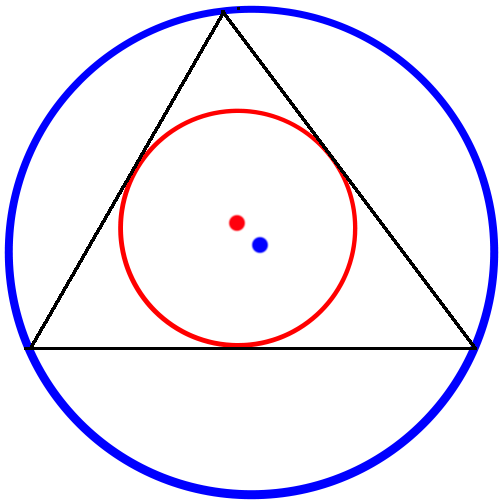
Quote: ThatDonGuyHere's a problem that's as easy or as hard as you want it to be
Triangle ABC has side lengths of 13, 14, and 15.
X is the center of the inscribed circle - that is, the circle that is tangent to all three sides. (In the image, it is in red.)
Y is the center of the circumscribed circle - that is, the circle that goes through A, B, and C. (In the image, it is in blue.)
What is the distance from X to Y?
If you want to make it easier, here are three hints:
The radius of the inscribed circle is 4
The radius of the circumscribed circle is 65/8link to original post
If AB has length 13 and BC has length 15, the distance from B to the point where the inscribed circle touches BC is 7.
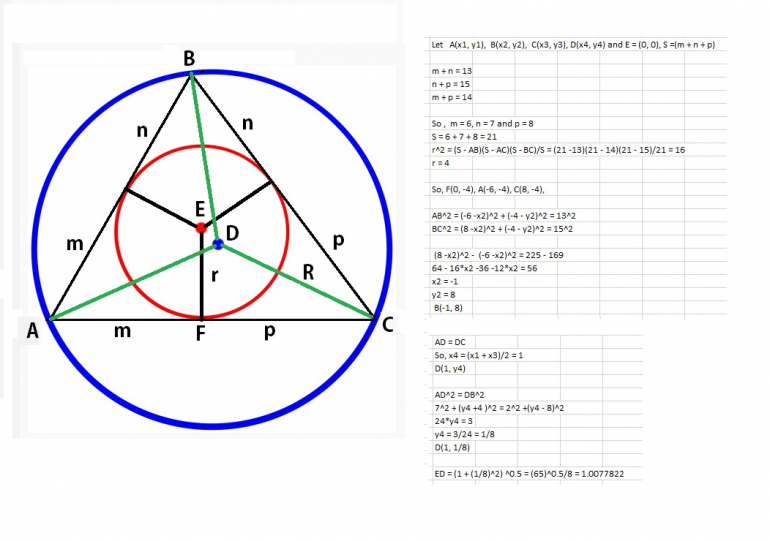
Let A(x1, y1), B(x2, y2), C(x3, y3), D(x4, y4) and E = (0, 0), S =(m + n + p)
m + n = 13
n + p = 15
m + p = 14
So , m = 6, n = 7 and p = 8
S = 6 + 7 + 8 = 21
r^2 = (S - AB)(S - AC)(S - BC)/S = (21 -13)(21 - 14)(21 - 15)/21 = 16
r = 4
So, F(0, -4), A(-6, -4), C(8, -4),
AB^2 = (-6 -x2)^2 + (-4 - y2)^2 = 13^2
BC^2 = (8 -x2)^2 + (-4 - y2)^2 = 15^2
(8 -x2)^2 - (-6 -x2)^2 = 225 - 169
64 - 16*x2 -36 -12*x2 = 56
x2 = -1
y2 = 8
B(-1, 8)
AD = DC
So, x4 = (x1 + x3)/2 = 1
D(1, y4)
AD^2 = DB^2
7^2 + (y4 +4 )^2 = 2^2 +(y4 - 8)^2
24*y4 = 3
y4 = 3/24 = 1/8
D(1, 1/8)
ED = (1 + (1/8)^2) ^0.5 = (65)^0.5/8 = 1.0077822
1. A total of seven is rolled.
2. A total of six is rolled twice.
3. A total of eight is rolled twice.
What is the probability the seven is rolled first?
((6 * 16 * 16) + (10 * 6 * 16) + (10 * 5 * 6)) / 16^3 = 699/1024
We can ignore all rolls besides 6, 7, and 8. Limited to these rolls, 7 comes up 3/8 of the time, and 6 and 8 each come up 5/16 of the time.
There are five sequences where 7 comes up before either 6 or 8 are rolled twice:
(a) 7 on the first roll - this has a probability of 3/8
(b) 6 followed by 7 - this has a probability of 5/16 x 3/8
(c) 8 followed by 7 - this has a probability of 5/16 x 3/8
(d) 6, then 8, then 7 - this has a probability of 5/16 x 5/16 x 3/8
(e) 8, then 6, then 7 - this has a probability of 5/16 x 5/16 x 3/8
The sum of these is 3/8 x (1 + 2 x 5/16 + 2 x 25/256) = 3/8 x (128 + 80 + 25) / 128 = 699 / 1024
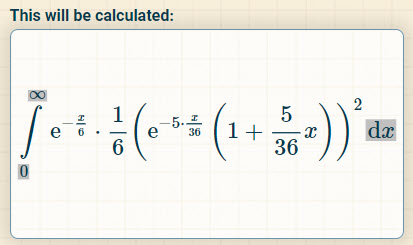
Quote: WizardI agree! I thought Ace would answer it as the solution to this integral.
link to original post
Since I have today off and I have nothing better to do, here's how to calculate it using calculus - as a bonus, there's a solution for a generic form used in equations like this:
The generic form:
What is the integral over x = 0 to positive infinity of x^n e^(-px) dx, where n is a positive integer and p > 0?
Integrate by parts:
u = x^n
du = n x^(n-1)
dv = e^(-px) dx
v = -1/p e^(-px)
The integral = -1/p x^n e^(-px) + n/p * the integral of (x^(n-1) e^(-px)) dx
= -1/p x^n e^(-px) + n/p * (-1/p x^(n-1) e^(-px) + (n-1)/p * the integral of (x^(n-2) e^(-px)) dx)
= ...
= -1/p x^n e^(-px) - n/p^2 x^(n-1) e^(-px) + n(n-1)/p^3 e^(-px) - ... - n!/p^(n+1) e^(-px)
= -1/p * e^(-px) * (x^n - n/p x^(n-1) + n(n-1)/p^2 - ... + (-1)^n n!/p^n)
Rewrite this as -1/p * (x^n - n/p x^(n-1) + n(n-1)/p^2 - ... + (-1)^n n!/p^n) / e^(px)
As x approaches positive infinity, the numerator and denominator both approach positive infinity
Apply L'Hôpital's Rule n times; the numerator is n! and the denominator approaches positive infinity, so the value approaches zero
This means the definite integral = 0 - (1/p * (-x^n + n/p x^(n-1) + n(n-1)/p^2 - ... + n!/p^n) / e^(px)) for x = 0
Since all of the x^k terms = 0, this is 1/p * n! / p^n
= n! / p^(n + 1)
As an example, using the 6/7/8 rolls problem:
Calculate the integral over x = 0 to positive infinity of {e^(-1/6 x) * 1/6 (e^(-5/36 x) * (1 + 5/36 x))^2 dx}
First, expand the problem:
1/6 e^(-1/6 x) * (e^(-5/36 x) * (1 + 5/36 x))^2
= 1/6 e^(-1/6 x) * e^(-5/18 x) * (1 + 5/18 x + 25/1296)
= 1/6 e^(-4/9 x) * (1 + 5/18 x + 25/1296)
= 1/6 e^(-4/9 x) + 1/6 * 5/18 x e^(-4/9 x) + 1/6 * 25/1296 x^2 e^(-4/9 x)
= 1/6 e^(-4/9 x) + 5/108 x e^(-4/9 x) + * 25/7776 x^2 e^(-4/9 x)
The integral is the sum of the integrals of the three separate parts of the sum
= 1/6 * 9/4 + 5/108 * (9/4)^2 + 2 * 25/7776 * (9/4)^3
= 3/8 + (5 * 9^2) / (9 * 12 * 16) + (2 * 25 * 3^6) / (3^5 * 2^5 * 2^6)
= 3/8 + 15/64 + 75/1024
= (384 + 240 + 75) / 1024
= 699 / 1024
d2y/dx2 = 1 / (1-y)
y= f(x) = ??
Quote: ssho88Can you help to solve this ? No solution ?
link to original post
d2y/dx2 = 1 / (1-y)
y= f(x) = ??
I can't help solve it, but WolframAlpha can.
A string is wound tightly around a rod, from one end to the other, making exactly five rotations around the rod. The rod is 40" long and has a circumference of 15." How long is the string?
Quote: WizardHere is an easy one while we work on sho88's more difficult problem.
link to original post
A string is wound tightly around a rod, from one end to the other, making exactly rotations around the rod. The rod is 40" long and has a circumference of 15." How long is the string?
Post missing number of rotations string makes.
Quote: unJonlink to original post
Post missing number of rotations string makes.
Nevermind that; how wide is the string?
Quote: unJonPost missing number of rotations string makes.
link to original post
Ooops. It makes five revolutions.
Quote: DieterNevermind that; how wide is the string?
link to original post
You may assume the width is negligible.
Quote: WizardHere is an easy one while we work on sho88's more difficult problem.
link to original post
A string is wound tightly around a rod, from one end to the other, making exactly five rotations around the rod. The rod is 40" long and has a circumference of 15." How long is the string?
It is similar to puzzle about the shortest travel distance from bottom of mountain to the peak of mountain.
Firstly, cut the rod/paper tube horizontally to form a rectangle shape, the height = circumference of 15", the length = 40', but there are 5 rotations, so the single length = 40/5 = 8,
The slant length = (15^2 + 8^2)^0.5 = 17", so total length of string = 5 x 17 = 85"
Quote: ssho88
It is similar to puzzle about the shortest travel distance from bottom of mountain to the peak of mountain.
Firstly, cut the rod/paper tube horizontally to form a rectangle shape, the height = circumference of 15", the length = 40', but there are 5 rotations, so the single length = 40/5 = 8,
The slant length = (15^2 + 8^2)^0.5 = 17", so total length of string = 5 x 17 = 85"
I agree!
Quote: ssho88Quote: WizardHere is an easy one while we work on sho88's more difficult problem.
link to original post
A string is wound tightly around a rod, from one end to the other, making exactly five rotations around the rod. The rod is 40" long and has a circumference of 15." How long is the string?link to original post
It is similar to puzzle about the shortest travel distance from bottom of mountain to the peak of mountain.
Firstly, cut the rod/paper tube horizontally to form a rectangle shape, the height = circumference of 15", the length = 40', but there are 5 rotations, so the single length = 40/5 = 8,
The slant length = (15^2 + 8^2)^0.5 = 17", so total length of string = 5 x 17 = 85"
That seems more complicated than necessary.
The string diagonally wound n times around the rod would be the hypotenuse of a triangle of height h and base n*circumference.
h=40; 5*circumference=75; apply pythagorean theorem.
Same answer, though.
Letís say youíre a $100 bettor that always takes 3/4/5 odds and you play a 2-point molly. What is your expected loss and standard deviation after 1,000 dice rolls?
Quote: ssho88Quote: ThatDonGuyHere's a problem that's as easy or as hard as you want it to be
Triangle ABC has side lengths of 13, 14, and 15.
X is the center of the inscribed circle - that is, the circle that is tangent to all three sides. (In the image, it is in red.)
Y is the center of the circumscribed circle - that is, the circle that goes through A, B, and C. (In the image, it is in blue.)
What is the distance from X to Y?
If you want to make it easier, here are three hints:
The radius of the inscribed circle is 4
The radius of the circumscribed circle is 65/8link to original post
If AB has length 13 and BC has length 15, the distance from B to the point where the inscribed circle touches BC is 7.link to original post
Let A(x1, y1), B(x2, y2), C(x3, y3), D(x4, y4) and E = (0, 0), S =(m + n + p)
m + n = 13
n + p = 15
m + p = 14
So , m = 6, n = 7 and p = 8
S = 6 + 7 + 8 = 21
r^2 = (S - AB)(S - AC)(S - BC)/S = (21 -13)(21 - 14)(21 - 15)/21 = 16
r = 4
So, F(0, -4), A(-6, -4), C(8, -4),
AB^2 = (-6 -x2)^2 + (-4 - y2)^2 = 13^2
BC^2 = (8 -x2)^2 + (-4 - y2)^2 = 15^2
(8 -x2)^2 - (-6 -x2)^2 = 225 - 169
64 - 16*x2 -36 -12*x2 = 56
x2 = -1
y2 = 8
B(-1, 8)
AD = DC
So, x4 = (x1 + x3)/2 = 1
D(1, y4)
AD^2 = DB^2
7^2 + (y4 +4 )^2 = 2^2 +(y4 - 8)^2
24*y4 = 3
y4 = 3/24 = 1/8
D(1, 1/8)
ED = (1 + (1/8)^2) ^0.5 = (65)^0.5/8 = 1.0077822
That is correct.
I solved it slightly differently:
Using your image, let A be on (0,0) and C on (14,0)
Let A be (0,0) and C be (14,0)
Law of Cosines: 225 = 169 + 196 - 364 cos A
cos A = 5/13
Let t be the measure of angle FAE: cos 2t = 5/13 = 2 cos^2 t - 1
cos^2 t = 9/13
sin^2 t = 1 - cos^2 t = 4/13
tan^2 t = (sin t / cos t)^2 = sin^2 / cos^2 t = 4/9
tan t = 2/3 = r/6, so r = 4, and E is at (6,4)
Let G be on AC such that DG is perpendicular to AC
DA = DC and DG = DG, so AGD and CGD are congruent (hypotenuse-leg)
AG = CG = AC / 2 = 7
AD = 65/8, so (DG)^2 = (AD)^2 - (AG)^2 = 65^2 / 64 - 49 * 64 / 64
DG = 33/8, so D is at (7, 33/8)
(DE)^2 = (7 - 6)^2 + (33/8 - 4)^2 = 1 + 1/64 = 65/64
DE = sqrt(65) / 8
Quote: Ace2A 2-point molly is when you make come bets until you have a total of two bets in play.
link to original post
Letís say youíre a $100 bettor that always takes 3/4/5 odds and you play a 2-point molly. What is your expected loss and standard deviation after 1,000 dice rolls?
My gut says to treat it as two different bets, so just calculate the EV and SD of one bet, then multiply the EV by 2 and the SD by sqrt(2). However, this doesn't take into account that the bets aren't necessarily independent; for example, if your first bet has a point of 4 and it is made on the next roll, you still have a bet with a point of 4 as a result of the second roll.
An "exact" EV, I can get, as there are only ten different "states" of bets (none; 4 or 10; 5 or 9; 6 or 8; 4 & 10; 5 & 9; 6 & 8; 4/10 & 5/9; 4/10 & 6/8; 5/9 & 6/8), and it is reduced to a set of equations. However, I don't know how to figure out the SD in this case, as I only know the "square root of the variance" (i.e. the square root of the sum of (probability of a particualr result x (value of the result - the mean result)^2)) method.
Itís easy to calculate how much the 2-point molly increases your total bets in a fixed period (80%). But I donít think you can just take the square root of 1.8 and say thatís how much the SD increases by. Many results will be correlated: for instance, if you have two points covered then a seven will cause both to lose at the same time. Or if you have one point covered and one bet on come, then a seven will make the point lose and the come bet win at the same timeQuote: ThatDonGuyQuote: Ace2A 2-point molly is when you make come bets until you have a total of two bets in play.
link to original post
Letís say youíre a $100 bettor that always takes 3/4/5 odds and you play a 2-point molly. What is your expected loss and standard deviation after 1,000 dice rolls?
My gut says to treat it as two different bets, so just calculate the EV and SD of one bet, then multiply the EV by 2 and the SD by sqrt(2). However, this doesn't take into account that the bets aren't necessarily independent; for example, if your first bet has a point of 4 and it is made on the next roll, you still have a bet with a point of 4 as a result of the second roll.
An "exact" EV, I can get, as there are only ten different "states" of bets (none; 4 or 10; 5 or 9; 6 or 8; 4 & 10; 5 & 9; 6 & 8; 4/10 & 5/9; 4/10 & 6/8; 5/9 & 6/8), and it is reduced to a set of equations. However, I don't know how to figure out the SD in this case, as I only know the "square root of the variance" (i.e. the square root of the sum of (probability of a particualr result x (value of the result - the mean result)^2)) method.link to original post
Covariance is a weak area for me. Hopefully the wizard will weigh in
Quote: Ace2A 2-point molly is when you make come bets until you have a total of two bets in play. ...
Forgive me as I'm still trying to work out other problem about five cottages, but was just wondering whether the original questioner continued to bet until two points were established at the same time. So you could have a row or points made or 7s meaning the first bet was being resolved and the second one went into the Come area (e.g. 4 4 4..., 4 7). Also do you make a Pass bet if the shooters point is immediately rerolled or they immediately 7-out, or do you wait until the next point is established - in the mean time the first bet could be resolved?Quote: ThatDonGuy...An "exact" EV, I can get, as there are only ten different "states" of bets (none; 4 or 10; 5 or 9; 6 or 8; 4 & 10; 5 & 9; 6 & 8; 4/10 & 5/9; 4/10 & 6/8; 5/9 & 6/8), and it is reduced to a set of equations...
I suspect mathematically the question is you make come bets (or pass bet) on the two rolls after the shooter establishes their first point. Where this results in two different points or a 7 somewhere, then there is some correlation. My feeling is, as per the above suggestion, you work out the different states and then just factor all the outcomes with their chances and their profit/loss (working out averages and SDs as appropriate).
You always bet if less than two bets are on the tableQuote: charliepatrickForgive me as I'm still trying to work out other problem about five cottages, but was just wondering whether the original questioner continued to bet until two points were established at the same time. So you could have a row or points made or 7s meaning the first bet was being resolved and the second one went into the Come area (e.g. 4 4 4..., 4 7). Also do you make a Pass bet if the shooters point is immediately rerolled or they immediately 7-out, or do you wait until the next point is established - in the mean time the first bet could be resolved?
link to original post
I suspect mathematically the question is you make come bets (or pass bet) on the two rolls after the shooter establishes their first point. Where this results in two different points or a 7 somewhere, then there is some correlation. My feeling is, as per the above suggestion, you work out the different states and then just factor all the outcomes with their chances and their profit/loss (working out averages and SDs as appropriate).
As an example, letís say thereís a new shooter and you bet $100 on pass, then a 4 is rolled. Then you put another $100 on come and a 4 is rolled again. Now you win $100, $100 travels from come to 4 and you put another $100 on pass. No more bets until you have less than two on the table
There are 3 basic states: 1) one bet on pass (no points established, happens only after a seven is rolled) ; 2) two total bets on pass/come (one point established) ; 3) two total bets on pass/come (two points established)
Incidentally, I like playing 2-Point molly since, assuming 100 rolls per hour, you get a bet resolved about once per minute instead of once per two minutes if only playing pass line. Though sometimes Iíll bet PL only for a larger amount. I want to know the 2 Point molly variance so I know how much to bet within my tolerance
Quote: Ace2A 2-point molly is when you make come bets until you have a total of two bets in play.
link to original post
Letís say youíre a $100 bettor that always takes 3/4/5 odds and you play a 2-point molly. What is your expected loss and standard deviation after 1,000 dice rolls?
A simulation of 3 million sets of 1000 rolls gives me a mean loss of about 725 and an SD of about 12,500.
If playing the passline only, we would expect 1000 * 165/557 =~ 296 bets resolved. That times 7/495 times $100 is an expected loss of ~ $419 with a SD of 296^.5 * 4.92 * $100 =~ $8,468Quote: ThatDonGuyQuote: Ace2A 2-point molly is when you make come bets until you have a total of two bets in play.
link to original post
Letís say youíre a $100 bettor that always takes 3/4/5 odds and you play a 2-point molly. What is your expected loss and standard deviation after 1,000 dice rolls?
A simulation of 3 million sets of 1000 rolls gives me a mean loss of about 725 and an SD of about 12,500.link to original post
We know that playing a 2-point molly increases our bets by a factor of 1.8. An average betting cycle lasts 7.5 rolls: 1.5 to establish a point plus 6 to roll a seven, There will be two bets in play except when no points have been established (6 / 7.5 = 80% of the time).
With a 2-point molly, the expected loss is $419 * 1.8 = $754. If the bets were independent, the SD would be $8,468 * 1.8^.5 = $11,361. But they are not independent, which is why Don's SD number came in higher at $12,500.
As we know, the expected edge on a passline bet with 3/4/5 odds is 1.41% with a SD of 4.92. On a per roll basis it's 0.419% with a SD of 2.68. The per-roll expected edge on a 2-point molly with 3/4/5 odds is 0.754% with a SD of 3.95
Thanks to ThatDonGuy for his simulation. However, I believe there is a straightforward way to calculate this formulaically. I'm still thinking of a way...the hard part is how to define the beginning/end of a "round" since new bets are being made often.
I just won a play money poker tournament, and my stats went from 33.5% tournaments won to 33.8% ó approximately how many tournaments have I played?
I appreciate your magical mathematical minds! (It's science, but it seems like magic!)
Quote: smoothgrhCan someone help me because I'm terrible at math?
link to original post
I just won a play money poker tournament, and my stats went from 33.5% tournaments won to 33.8% ó approximately how many tournaments have I played?
I appreciate your magical mathematical minds! (It's science, but it seems like magic!)
Let w = number of wins; N = number of tournaments.
Then:
w / N = 0.335
(w + 1) / (N + 1) = 0.338
Solution:
w = 73.9; N = 220.7
It looks like you had won about 74 out of 221 tournaments. And then you won another to make your record 75 out of 222.
(Check: 74 / 221 = 33.48%; 75 / 222 = 33.78%.)
Quote: Ace2Thanks to ThatDonGuy for his simulation. However, I believe there is a straightforward way to calculate this formulaically. I'm still thinking of a way...the hard part is how to define the beginning/end of a "round" since new bets are being made often.
link to original post
Is there a way of calculating the SD without being able to establish a finite set of profits, and a probability for each one, in any given round?
I am assuming a round begins when you have no outstanding points (i.e. either you rolled a 7, or you only had one point outstanding and you just made it).
If your first roll is a 5, then you roll any combination of 2s, 3s, 5s, 11s, and 12s, you remain in the "one point of 5" state, but the profit value can be pretty much anything. (For example, if the rolls are 5, 5, 12, then you made $700 on the first five and lost $100 on the 12, so your current profit is $600; if they are 5, 11, 3, 5, 11, you made $100 on the first 11, lost it back on the 3, made $700 on the second 5, and made another $100 on the 11, so your current profit is $800. In both cases, after every roll, you had one point of 5, but no second point.)
Arrange n^3 small cubes into one large cube. Then paint one or more of the large cube's faces. How many small cubes are there (or "What is n"), and which large faces were painted if we find:
a) Exactly 52% of the small cubes have paint on at least one face.
b) Exactly 36% of the small cubes have paint on at least one face.
c) Exactly 8% of the small cubes have paint on at least one face.

Quote: GialmereArrange n^3 small cubes into one large cube. Then paint one or more of the large cube's faces. How many small cubes are there (or "What is n"), and which large faces were painted if we find:
a) Exactly 52% of the small cubes have paint on at least one face.
b) Exactly 36% of the small cubes have paint on at least one face.
c) Exactly 8% of the small cubes have paint on at least one face.
If one face is painted, then n^2 of the cubes are painted
If two faces are painted, and
(a) they do not share an edge, then 2 n^2 of the cubes are painted;
(b) they share an edge, then 2 n^2 - n of the cubes are painted
If three faces are painted, and
(a) two of them are opposite, then the third shares separate edges with each of them, so 3 n^2 - 2 n of the cubes are painted;
(b) none of them are opposite, then they share a vertex, and 3 n^2 - 3 n + 1 of the cubes are painted
If four faces are painted, then either:
(a) they form a "ring", and 4 n^2 - 4 n cubes are painted, or
(b) one shares edges with each of the other three, so 4 n^2 - 5 n + 2 of the cubes are painted
If five faces are painted, then 6 n^2 - (n - 2)^2 = 5 n^2 + 4 n - 4 of the cubes are painted
If six faces are painted, then n^3 - (n - 2)^3 = 6 n^2 - 12 n + 8 of the cubes are painted
52% is 125 small cubes; three sides that do not share a vertex were painted
36% has two answers:
125 small cubes, with two sides that share an edge painted;
1000 small cubes, with four sides that form a "ring" (i.e. no three sides share a vertex) painted
8% is 625 with two opposite sides painted
Quote: ThatDonGuy
If one face is painted, then n^2 of the cubes are painted
If two faces are painted, and
(a) they do not share an edge, then 2 n^2 of the cubes are painted;
(b) they share an edge, then 2 n^2 - n of the cubes are painted
If three faces are painted, and
(a) two of them are opposite, then the third shares separate edges with each of them, so 3 n^2 - 2 n of the cubes are painted;
(b) none of them are opposite, then they share a vertex, and 3 n^2 - 3 n + 1 of the cubes are painted
If four faces are painted, then either:
(a) they form a "ring", and 4 n^2 - 4 n cubes are painted, or
(b) one shares edges with each of the other three, so 4 n^2 - 5 n + 2 of the cubes are painted
If five faces are painted, then 6 n^2 - (n - 2)^2 = 5 n^2 + 4 n - 4 of the cubes are painted
If six faces are painted, then n^3 - (n - 2)^3 = 6 n^2 - 12 n + 8 of the cubes are painted
52% is 125 small cubes; three sides that do not share a vertex were painted
36% has two answers:
125 small cubes, with two sides that share an edge painted;
1000 small cubes, with four sides that form a "ring" (i.e. no three sides share a vertex) painted
8% is 625 with two opposite sides painted
Correct!!!
Very good.
-------------------------------------------------------------

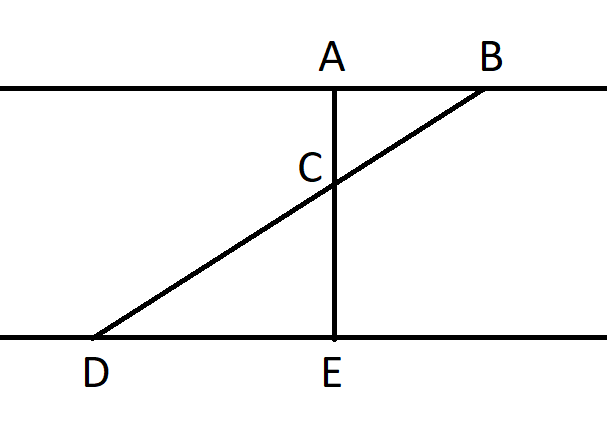
You are given:
AB is parallel to DE
AE is perpendicular to DE
DE = 315
AE = 336
BD = 636
What is AB?
Quote: WizardYou are given:
link to original post
AB is parallel to DE
AE is perpendicular to DE
DE = 315
AE = 336
BD = 636
What is AB?
Let F be the point on line DE such that BF is perpendicular to DF (and parallel to AE as a result); BF = AE = 336
Pythagorean Theorem: (DF)^2 = (BD)^2 - (AE)^2 = 636^2 - 336^2 = 540^2
AB = EF = DF - DE = 540 - 315 = 225
Quote: ThatDonGuyQuote: WizardYou are given:
link to original post
AB is parallel to DE
AE is perpendicular to DE
DE = 315
AE = 336
BD = 636
What is AB?link to original post
Let F be the point on line DE such that BF is perpendicular to DF (and parallel to AE as a result); BF = AE = 336
Pythagorean Theorem: (DF)^2 = (BD)^2 - (AE)^2 = 636^2 - 336^2 = 540^2
AB = EF = DF - DE = 540 - 315 = 225
I agree!
Quote: Wizard...What is AB?
link to original post
BD2=BF2+DF2. Dividing each side by 12 gives a 53/45/28 triangle. So DF=45*12=540.
So EF = 540-315=225. This is equal to AB (by construction).
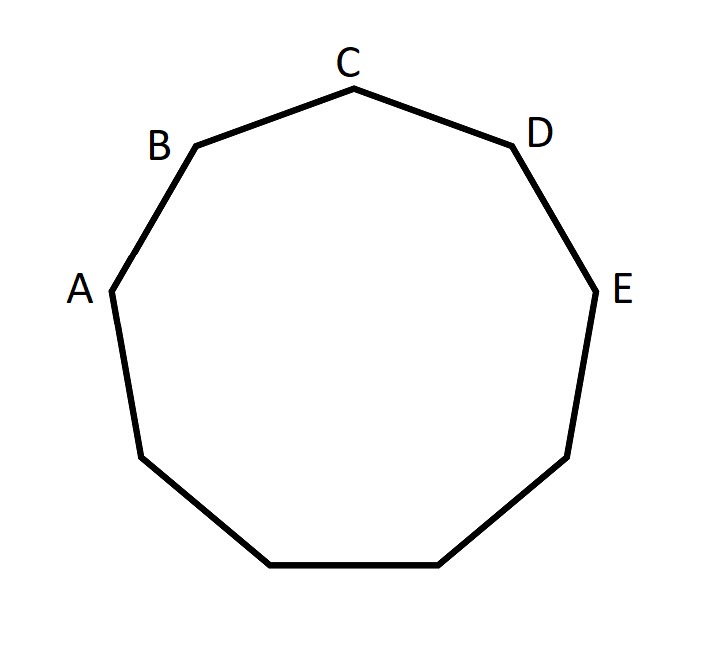
The figure above is a nonagon with side length one.
What is (AB+AC)/AE?
Call O = center.
Call R = distance from O to A
For any triangle section defined by AO(_). where (_) = B, C, or E
.5 * dist(A(_)) = R sin (.5 * angle (AO(_)) from trig.
Since 9 sections
angle(AOB) = 40 degrees
angle(AOC) = 80 degrees
angle(AOE) = 160 degrees
So
AB= 2R sin(20)
AC= 2R sin(40)
AE= 2R sin(80)
(AB + AC)/AE = {sin(20) + sin(40)} / sin(80) = 1 ***
***Calculator tells me it is 1....can't see the trig to get it...missing something....going to sleep on it to see if it comes to me in morning
Quote: chevylink to original post
Call O = center.
Call R = distance from O to A
For any triangle section defined by AO(_). where (_) = B, C, or E
.5 * dist(A(_)) = R sin (.5 * angle (AO(_)) from trig.
Since 9 sections
angle(AOB) = 40 degrees
angle(AOC) = 80 degrees
angle(AOE) = 160 degrees
So
AB= 2R sin(20)
AC= 2R sin(40)
AE= 2R sin(80)
(AB + AC)/AE = {sin(20) + sin(40)} / sin(80) = 1 ***
***Calculator tells me it is 1....can't see the trig to get it...missing something....going to sleep on it to see if it comes to me in morning
I agree with the answer of 1. Where I'm at now is trying to prove it.
Here is the way I express it:
AB+AC = AE
1+2cos(20) = 4*cos(40)cos(20)
I also know cos(2x)=cos^2(x)-sin^2(x), but so far it's not helping.
The question at hand, now, is why is his answer right. I have solved it (with some cheating). At this point, I'll wait to see what the forum comes up with. This is definitely a beer problem and shouldn't have been filed under "easy problems."
In fact, I should make a separate thread for "beer problems."
There is a formula for adding Sines sin(x)+sin(y)=2*sin((x+y)/2)*cos((x-y)/2).
So SIN(20)+SIN(40) = 2 * SIN(30) * COS(10) = 2 * 1/2 * COS(10) = COS(10).
But COS(x)=SIN(90-x), so COS(10) = SIN(80).
Quote: Wizard
link to original post
I agree with the answer of 1. Where I'm at now is trying to prove it.
Here is the way I express it:
AB+AC = AE
1+2cos(20) = 4*cos(40)cos(20)
I also know cos(2x)=cos^2(x)-sin^2(x), but so far it's not helping.
I got to your point as well using sin2x = 2 sinx cosx. a couple times. Got stuck At cos2x as well.
I can also change it to sin's using cos(x)=sin(90-x)
(1+2sin(70) )/(4 sin(50) sin(70))
which made me think of playing with sin(a+b) type things (70=50+20) etc. but still no luck
Quote: charliepatricklink to original postIt has already been shown that the proof relies on looking at SIN(20)+SIN(40) and whether it equals SIN(80).
There is a formula for adding Sines sin(x)+sin(y)=2*sin((x+y)/2)*cos((x-y)/2).
So SIN(20)+SIN(40) = 2 * SIN(30) * COS(10) = 2 * 1/2 * COS(10) = COS(10).
But COS(x)=SIN(90-x), so COS(10) = SIN(80).
Thanks charliepatrick.
That identity is way too far down the list for me to recall on my own at this point in life.
You may recall my last spoiler said:
1+2cos(20) = 4*cos(40)cos(20)
I was trying to prove that in general 1 + 2cos(x) = 4cos(2x)*cos(x)
It turns out, this is not generally true, but happens to be true for x=20. That is what messed me up.
I will say there is an elegant solution to this that does not involve obscure trigonometry formulas. I think the whole thing can be solved with just knowing the angles of a triangle sum to 180.
Warning -- There is an "a-ha" moment you need to get to.
If everybody gets stuck, I'll provide a hint.
Quote: Wizard...There is an "a-ha" moment you need to get to...
Consider centre of the diagram as O and consider the various triangles using radii and the edges OAB, OBC etc which are all 40-70-70 (as 360/9 = 40). Thus Angle AOE is 160 (4*40), so OAE=10, so EAB=AED=60.
Construct an equilateral triangle ABX (where X lies on AE). So AX=AB (by construction).
By symmetry BD is parallel to AE, and BX is parallel to DE, so XE=BD.
Thus AB+AC=AB+BD=AX+XE=AE.
Quote: charliepatricklink to original postThe side AC is the same length as BD, so just need to prove AB+BD=AE.
Consider centre of the diagram as O and consider the various triangles using radii and the edges OAB, OBC etc which are all 40-70-70 (as 360/9 = 40). Thus Angle AOE is 160 (4*40), so OAE=10, so EAB=AED=60.
Construct an equilateral triangle ABX (where X lies on AE). So AX=AB (by construction).
By symmetry BD is parallel to AE, and BX is parallel to DE, so XE=BD.
Thus AB+AC=AB+BD=AX+XE=AE.
Yes, that is the same realization I used to get to the answer too. I might phrase it a little differently, but the logic is the same.
Let c = Beers I owe Charlie.
c++;