Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Applying my conjecture that the probability of reaching a point at any time during a session is double the probability of ending the session at/beyond that point , we need the z-score corresponding to the probability of 1/3 * 1/2, which is 0.967. Then take 1200^.5 * 1.1547 * 0.967 to get the answer of 38.7 units * $500 = $19,350.Quote: Ace2You go to Vegas over a long weekend to play a single-deck blackjack game with a 0% edge ($500 minimum). You decide to play 1,200 hands but you will quit if you bust or double your initial bankroll before reaching 1200 hands.
What size bankroll should you bring to give yourself a 1/3 chance of busting, 1/3 chance of doubling and 1/3 chance of finishing the 1200 hands without busting or doubling?
Assume a standard deviation of 1.1547, flat betting $500 one hand at a time and perfect basic strategy to realize the 0% edge
link to original post
Verification: Knowing the standard deviation and edge, you can easily calculate that this game is statistically equivalent to a bet with a 3/7 probability of winning 7 for 3. Markoving 1200 bets shows that a bankroll of 38 units * $500 = $19,000 gives bust/double/finish probabilities of 33.4%/33.4%/33.2%. I believe this is the closest you can get to 1/3.
So I'd bring $20,000
Gin and Win
The object of trying to put as many cards as you can in sets, with the goal of minimizing dead wood, is also the goal of Gin and Win. It should be emphasized that pairs and flushes of at least three cards count as sets in Gin and Win. The rules start as follows:
1. Cards are ranked as in poker, except aces are low only.
2. To begin, each player must post an Ante bet.
3. The player and dealer are each dealt seven cards, face down, from a normal 52 card deck.
4. The player looks at his hand and removes any combinations of pairs, trips, and quads (rank melds), or any flushes of three cards or more cards (suit melds). One card cannot be part of more than one set.
5. The remaining cards are known as "Dead Wood" and are set apart from the cards that belong to a set.
Math puzzle:
With what probability will a player be dealt a hand with "no sets" and thus have seven Dead Wood cards?
With what probability will a player be dealt a hand with exactly five Dead Wood cards?
The second part is that to get no flushes the suits have to be divided 2-2-2-1. There are four ways to pick the singleton suit, so let's assume it's Clubs, thus the doubletons are Spades, Hearts and Diamonds. There are seven different ranks, so the ways to assign the Spades to them is 7*6/2=21. This leaves five non-Spades. The ways to assign Hearts is 5*4/2=10. Similarly Diamonds = 3*2/2=3. Leaving the Club assignment. The total number of ways for the suits is 4 * 21 * 10 * 3 * 1 = 2520.
Of the 1716 ways for seven different ranks, only 393 have no possible 3-card straights (I could only do that using a spreadsheet).
So there are 393*2520 hands = 990,360.
The total number of ways to have 7 cards from 52 is 133,784,560.
So the chances of such a hands = 990,360 / 133,784,560 which is about 0.7% (or one hand in 135).
13 * combin(12,5) * (12*10*3) / combin(52,7)
Quote: Ace25 deads
13 * combin(12,5) * 16 / combin(52,7)
link to original post
In order to have exactly 5 dead cards, two of your cards must be a pair, and the other 5 cards must have no pairs and your seven cards must have no more that 2 cards in any given suit.
Quote: Ace2^^^Thatís exactly what I calculated, though I did edit my answer
link to original post
Well you got the denominator right, lol. I am struggling with your numerator.
Try answering the question about 7 deads, which may illuminate the path to wisdom on 5 Deads.
Quote: gordonm888This easy math puzzle is based on the rules of Gin and Win.
Gin and Win
The object of trying to put as many cards as you can in sets, with the goal of minimizing dead wood, is also the goal of Gin and Win. It should be emphasized that pairs and flushes of at least three cards count as sets in Gin and Win. The rules start as follows:
1. Cards are ranked as in poker, except aces are low only.
2. To begin, each player must post an Ante bet.
3. The player and dealer are each dealt seven cards, face down, from a normal 52 card deck.
4. The player looks at his hand and removes any combinations of pairs, trips, and quads (rank melds), or any flushes of three cards or more cards (suit melds). One card cannot be part of more than one set.
5. The remaining cards are known as "Dead Wood" and are set apart from the cards that belong to a set.
Math puzzle:
With what probability will a player be dealt a hand with "no sets" and thus have seven Dead Wood cards?
With what probability will a player be dealt a hand with exactly five Dead Wood cards?
link to original post
gordonm888,
I see no mention of straights in item 4. Do they not count in Gin and Win?
Dog Hand
Quote: DogHandI see no mention of straights in item 4. Do they not count in Gin and Win?
link to original post
No, they do not. See part 5 of this Nevada Gaming Commission document about the game.
Quote: ThatDonGuyQuote: DogHandI see no mention of straights in item 4. Do they not count in Gin and Win?
link to original post
No, they do not. See part 5 of this Nevada Gaming Commission document about the game.
link to original post
That is correct.
Dog Hand
13 *6 * combin(12,5) * (4*3*10*3) / combin(52,7)
13 * 6 ways to choose the pair
C(12,5) ways to choose ranks of the five
4*3 ways to choose suits of the five (221)
10*3 ways to assign the suits to the five
Caveat: combinatorics arenít my strongest skill
Quote: charliepatrickThe first part is to get no pairs, all the ranks of the cards have to be different. At a later stage let's look at which of those could make a 3-card straight.
The second part is that to get no flushes the suits have to be divided 2-2-2-1. There are four ways to pick the singleton suit, so let's assume it's Clubs, thus the doubletons are Spades, Hearts and Diamonds. There are seven different ranks, so the ways to assign the Spades to them is 7*6/2=21. This leaves five non-Spades. The ways to assign Hearts is 5*4/2=10. Similarly Diamonds = 3*2/2=3. Leaving the Club assignment. The total number of ways for the suits is 4 * 21 * 10 * 3 * 1 = 2520.
Of the 1716 ways for seven different ranks, only 393 have no possible 3-card straights (I could only do that using a spreadsheet).
So there are 393*2520 hands = 990,360.
The total number of ways to have 7 cards from 52 is 133,784,560.
So the chances of such a hands = 990,360 / 133,784,560 which is about 0.7% (or one hand in 135).
link to original post
To confirm the comments of others, in this puzzle (and in Gin and Go) one cannot meld straights.
Quote: charliepatrick^ I erroneously had assumed it was like regular gin. It does make the maths easier as you donít have to check the unequal ranks.
So instead of 393*2520 itís 1716*2520 giving 4,324,320 or about 3.23%.
link to original post
I get a slightly higher answer. I am having difficulty critiquing your answer because you have used numbers rather than formulas such as c(n,m) for combinations.
The second number is how many ways the suits of seven different cards can happen so the suit distribution is 2-2-2-1.
The first part is that there can be four suits for the singleton, and once that has been determined then the other suits are fixed.
The next part is how those suits can be distributed onto the ranks.
The singleton can be put in one of 7 positions.
The highest of the other three suits can be put in 6*5/2 of the remaining 6 positions.
Similar the next suit can be put in 4*3/2 of the remaining positions.
The last suit is now set.
So you have 4 * 7 * 6*5/2 * 4*3/2 * 1 = 2520.
2520 * 1716 = 4324320.
7 | 4 | 6 864 | |||
6 | 1 | 84 | 144 144 | ||
5 | 2 | 252 | 432 432 | ||
5 | 1 | 1 | 504 | 864 864 | |
4 | 3 | 420 | 720 720 | ||
4 | 2 | 1 | 2 520 | 4 324 320 | |
4 | 1 | 1 | 1 | 840 | 1 441 440 |
3 | 3 | 1 | 1 680 | 2 882 880 | |
3 | 2 | 2 | 2 520 | 4 324 320 | |
3 | 2 | 1 | 1 | 5 040 | 8 648 640 |
2 | 2 | 2 | 1 | 2 520 | 4 324 320 |
Quote: Ace2One more revision for five deads
13 *6 * combin(12,5) * (4*3*10*3) / combin(52,7)
13 * 6 ways to choose the pair
C(12,5) ways to choose ranks of the five
4*3 ways to choose suits of the five (221)
10*3 ways to assign the suits to the five
Caveat: combinatorics arenít my strongest skill
link to original post
I also believe this is not correct.
Let me point out that if one of the paired cards can be used to make a three card flush in your hand, then you would meld the three card flush because it would give you 4 deadwood cards rather than the five deads that result from melding the pair.
Charlie's answer is correct. See my next post.
Quote: charliepatrickFirstly there are how many ways can you make 7 different ranks from 13, which is 13 12 11 10 9 8 7 / (7 6 5 4 3 2 1) = 1716.
The second number is how many ways the suits of seven different cards can happen so the suit distribution is 2-2-2-1.
The first part is that there can be four suits for the singleton, and once that has been determined then the other suits are fixed.
The next part is how those suits can be distributed onto the ranks.
The singleton can be put in one of 7 positions.
The highest of the other three suits can be put in 6*5/2 of the remaining 6 positions.
Similar the next suit can be put in 4*3/2 of the remaining positions.
The last suit is now set.
So you have 4 * 7 * 6*5/2 * 4*3/2 * 1 = 2520.
2520 * 1716 = 4324320.
link to original post
Charlie's answer is correct!
To have 7 dead wood in a 7 card hand there must be no flushes of 3 or more cards, and seven different ranks.
A 7 card hand with no flushes (3 or more cards) can have only one distribution of suites: 2-2-2-1 with four variations corresponding to which of the four suits has only on card.
First, ignoring pairing, let's write a formula for the number of combinations of seven card hands with no qualifying flushes, given that it must be a 2-2-2-1 distribution of cards in the four suits.
= 4* c(13,2)* c(13,2)* c(13,2)*c(13,1) = 24,676,704
This value includes hands with paired cards and less that 7 deadwood. It's simple to modify this formula to require that the 7-card hand with a 2-2-2-1 suit distribution has 7 distinct ranks; i.e., no pairing:
=4* c(13,2)*c(11,2)*c(9,2)*COMBIN(7,1) = 4,324,320
So, the frequency of a 7-deads hand = 4* c(13,2)*c(11,2)*c(9,2)*COMBIN(8,1) /c(52,7) = 0.032323012
The second part of the puzzle is for the probability of getting a hand with 5 deadwood cards. I used the first formula in this derivation as a starting point for the 5 deads calculation.
There are 10296 ways to have one rank that is the pair and five other ranks (13 * (12*11*10*9*8/5/4/3/2/1) ).
There are then 6144 (6*4*4*4*4*4) to have the suits arranged, six ways for the pair, and four for each singleton.
The same logic produces...11119680/133784560 = about 8.31%
7 | |||||
6 | 1 | 12 | 123 552 | ||
5 | 2 | 60 | 617 760 | ||
5 | 1 | 1 | 132 | 1 359 072 | |
4 | 3 | 120 | 1 235 520 | ||
4 | 2 | 1 | 840 | 8 648 640 | |
4 | 1 | 1 | 1 | 300 | 3 088 800 |
3 | 3 | 1 | 600 | 6 177 600 | |
3 | 2 | 2 | 960 | 9 884 160 | |
3 | 2 | 1 | 1 | 2 040 | 21 003 840 |
2 | 2 | 2 | 1 | 1 080 | 11 119 680 |
Btw 11119680 is exactly 1/2 of my answer
For the 1111111 rank distribution (i.e. no pairs) its essentially like creating numbers of base 4. So there are 47 lines.
For the 211111 rank distribution (i.e. one pair) the last five columns are as above, but the first two start with 12, then go 13, 14, 23, 24, 34. Thus there are 6*45 lines.
For each line I then count how many 1s, 2s, 3s and 4s there are, and create four digit numbers such as 7000, 6100, 5200, 5110 etc for the suit distribution. I then count how many of these there are.
For the pairs I looked at the simple cases e.g. 6100 is where the odd suit has to be one of the pairs, and all the other cards are in the same suit. So there are 4*3 of them.
Since the numbers added up to 6144, I didn't check the more complicated ones.
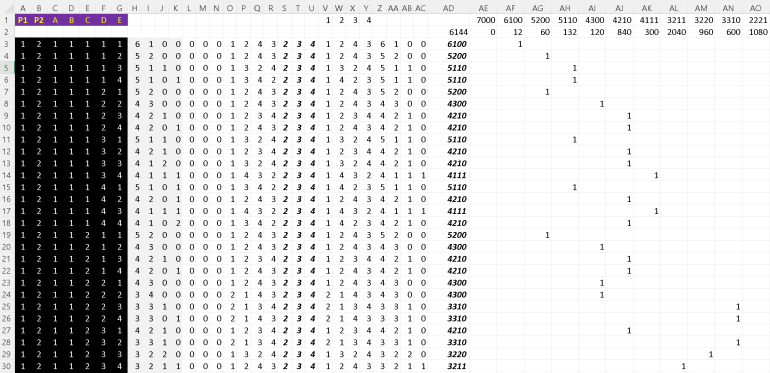
Quote: charliepatrick^ I've now developed a spreadsheet which essentially creates every combination of how the suits are given to the various ranks.
For the 1111111 rank distribution (i.e. no pairs) its essentially like creating numbers of base 4. So there are 47 lines.
For the 211111 rank distribution (i.e. one pair) the last five columns are as above, but the first two start with 12, then go 13, 14, 23, 24, 34. Thus there are 6*45 lines.
For each line I then count how many 1s, 2s, 3s and 4s there are, and create four digit numbers such as 7000, 6100, 5200, 5110 etc for the suit distribution. I then count how many of these there are.
For the pairs I looked at the simple cases e.g. 6100 is where the odd suit has to be one of the pairs, and all the other cards are in the same suit. So there are 4*3 of them.
Since the numbers added up to 6144, I didn't check the more complicated ones.
link to original post
I've read this through many many times and studied your table and I do now understand what you've done. Very impressive. You've figured out the probabilities of all the suit distributions for the "1 pair + 5 singletons" case. In the first seven columns the numerals 1-4 refer to suits of the seven cards P1,P2,A,B,C,D,E in a 'one pair+5 singletons' hand.
Again, very impressive. Your answer for 5 deads agrees with mine, but I took a simpler approach to get there.
My approach was to start with the idea that a 5 deadwood hand must have a 2221 suit distribution and then analyze how often such a suit distribution will consist of one pair and 5 singletons.
There are three possibilities to form the one pair in a 2221 suit distribution:
- the second suit has a card that pairs with one of the 2 cards in the first suit,or
- the third suit has a card that pairs with one of the 4 cards in the first two suits, or
- the only card in the fourth suit pairs with one of the 6 cards in the first three suits
Hence the combinatorial formula is:
=4*(COMBIN(13,2)* COMBIN(11,1)*2* COMBIN(10,2)* COMBIN(8,1)+ COMBIN(13,2)* COMBIN(11,2)* COMBIN(9,1)*4* COMBIN(8,1)+ COMBIN(13,2)* COMBIN(11,2)* COMBIN(9,2)*6)/ COMBIN(52,7)
= 0.083116318
And CharliePatrick's result agrees with this.
I felt the key insight was to understand that the suit distribution was 2221 for both the 7 deads and 5 deads case and then to modify that combinatorial formula for the case of no pairs and one pair.
Quote: Ace2Another truly easy math problem:
You flip a fair coin one million times. Whatís the probability of getting exactly 501,000 heads ?
link to original post
Sorry for the late arrival.
I was going to say COMBIN(1000000,501000)*(1/2)^1000000 (using Excel notation), but this is evidently outside of Microsoft's abilities.
Using the Normal approximation, which I know you won't accept, I get 1 in 9,261.
I'll be interested to see your approach.
I see my own WizCalc can handle this. Score a point for the much underappreciated JB. It gives an answer of 0.0001079819780189151621325412194348372338575688419910325533021609955515060572694514384816325574020949003535696616274753950196154216862415243735543855288530841354150737835401503902003382365657881979241065873081237507581076201738969307002842985156610741880773089.
I don't think it's going to get much better than that.
Quote: WizardReply #2 to coin flip problem.
I see my own WizCalc can handle this. Score a point for the much underappreciated JB. It gives an answer of 0.0001079819780189151621325412194348372338575688419910325533021609955515060572694514384816325574020949003535696616274753950196154216862415243735543855288530841354150737835401503902003382365657881979241065873081237507581076201738969307002842985156610741880773089.
I don't think it's going to get much better than that.
link to original post
This is to 1000 digits in the denominator; the actual result has 301,032 digits, but the forum software won't let me post something that large
2 61008 89729 60608 29636 91108 00206 68025 00342 52113
27656 05029 61456 90126 00865 12774 08879 00559 36453 99394
36060 77802 59145 81984 24930 86158 58481 28037 99635 49871
73474 26909 45688 44147 05790 01546 32778 41987 51029 43813
75502 31273 53846 79253 17551 42623 85920 81872 01893 80470
93232 60355 64881 65381 47080 37662 66709 34240 72787 00821
75948 23175 43323 10020 06426 30360 58671 43206 28981 12134
29574 17148 66487 76159 59908 21303 40360 14123 61867 75837
91069 77068 56803 86292 99141 24409 17447 97129 56832 99772
55757 95321 27753 75096 72536 33663 12365 03304 28574 15093
03575 50064 89265 99071 16274 38342 63318 12068 69530 92391
04209 17400 55340 60378 19882 09243 77371 18638 50814 66464
67514 31088 41579 08129 36973 61737 80061 28918 66268 07184
38913 78801 45818 42700 23976 89104 24572 70572 14859 89495
09172 13887 94658 11506 06406 99599 89903 65290 32334 35675
59159 09923 38404 16365 36153 19318 74646 74027 17393 75511
90242 61503 52658 64386 03131 38421 05444 99886 48764 40597
90240 60957 25985 81349 24470 91436 58989 99430 71164 17725
25916 39781 80127 45872 12686 29695 37168 95894 02600 02188
12105 53119 49803 08033 56147 48031 32558 30127 21425 95495
/
24171 52399 73044 39088 61797 75788 62068 48323 63873 09051
67805 87558 49888 99343 13557 36050 05628 56800 56725 21579
95176 55046 47115 16696 37477 19479 83796 75115 77774 66591
13538 50662 80990 65509 94085 81413 90781 83342 31587 96177
95316 09285 60576 63240 01557 43159 31642 51468 17067 77478
77698 69792 91946 37110 87871 53144 49041 31436 59746 79262
85581 80970 92682 58256 94051 45800 82506 08688 97875 85793
39624 78644 26694 19699 61315 75049 75202 43572 11378 88952
13705 01523 75882 37180 79259 35612 90552 51591 48601 45103
67007 85042 65938 19162 21795 96263 82791 40872 09946 87561
28079 45110 26672 23989 07049 73577 19917 25962 19813 36993
23379 47757 32383 79366 99527 19822 51061 48395 29907 23028
90437 50559 11196 02309 99094 32877 57564 02161 93031 51226
47626 67877 97715 01508 34886 90342 56169 06080 06663 74947
85643 97719 40410 85894 04127 56060 31090 10376 82121 07231
81736 26843 52850 53520 58182 79891 68565 62929 84990 65899
65831 60682 97268 76281 78493 13205 21480 80624 90016 87080
54315 24506 41398 76028 86021 02634 93660 78221 44485 43786
68220 50569 63599 50444 97978 87127 06877 51184 61516 83774
08554 66959 37447 69963 97488 94320 15192 82683 42189 05279

Quote: charliepatrickI spotted this lovely puzzle on facebook (sorry if you've already seen it).
link to original post
I think I can do that!
1. You will eliminate half the deck, and your guess will hit 1/26 times, 0.03846
2. 3/13 times you will have a 1/12 chance, and 10/13 times you will have a 1/40 chance. (3/13)(1/12)+(10/13)(1/40)=0.03846
3. 1/52 times you will have a 1 chance, and 51/52 times you will have a 1/51 chance. (1/52)+(51/52)(1/51)=0.03846
So the correct answer is 2.
Because there is more likely to be some confusion about "face card" if the card is a 10, assuming the friend has played blackjack or baccarat. So if he does a double take, hesitates, or seems like he is thinking about if a 10 counts as a face card I'm going to guess one of the Tens. Just a little mentalism. Worth something, not much.
Quote: charliepatrickI spotted this lovely puzzle on facebook (sorry if you've already seen it).
link to original post
#1 will reduce the chance to 1/26 regardless of the result
#2 has a 3/13 chance of giving you a 1/12 chance, and a 10/13 chance of giving you a 1/40 chance, so P = 3/13 x 1/12 + 10/13 x 1/40 = 1/26
#3 has a 1/52 chance of giving you a 100% chance and a 51/52 chance of giving you a 1/51 chance, so P = 1/52 + 51/52 x 1/51 = 1/26
Any of the three reduces the probability to 1/26
General case:
"Is the card in this set of N cards?"
There is an N/52 chance that it is, in which case there is a 1/N chance of guessing correctly
There is a (52 - N)/52 chance that it is not, in which case there is a 1/(52 - N) chance of guessing correctly
The probability is N/52 x 1/N + (52 - N)/52 x 1/(52 - N) = 1/26
You could make a similar argument picking number 3. If your friend hesitates /double takes before saying no, thereís a greater chance the card is an Ace of Clubs, 4 of spades or 4 of clubs, which are the cards that most resemble Ace of spadesQuote: AutomaticMonkeyQuote: charliepatrickI spotted this lovely puzzle on facebook (sorry if you've already seen it).
link to original post
I think I can do that!
1. You will eliminate half the deck, and your guess will hit 1/26 times, 0.03846
2. 3/13 times you will have a 1/12 chance, and 10/13 times you will have a 1/40 chance. (3/13)(1/12)+(10/13)(1/40)=0.03846
3. 1/52 times you will have a 1 chance, and 51/52 times you will have a 1/51 chance. (1/52)+(51/52)(1/51)=0.03846
So the correct answer is 2.
Because there is more likely to be some confusion about "face card" if the card is a 10, assuming the friend has played blackjack or baccarat. So if he does a double take, hesitates, or seems like he is thinking about if a 10 counts as a face card I'm going to guess one of the Tens. Just a little mentalism. Worth something, not much.
link to original post
I canít think of any way to gain an edge picking number 1. Hard to confuse red and black
Only closed-form solutions are beer-worthy
Quote: Ace2You roll a six-sided die thirty times. Whatís the probability you donít roll any consecutive fives?
Only closed-form solutions are beer-worthy
link to original post
I used a Markov chain to get 107,932,636,085,236,000,000,000 / 221,073,919,720,733,000,000,000 =~ 0.48821967. Note I was rebuffed my Excel's limit of 15 significant digits. I can explain the method in more detail upon request, but it was quite easy in Excel.
Hopefully I will get partial credit.
I agree with your answer but it needs to be closed-form for full credit. The answer is easy to obtain with a 2 column x 30 row Markov chainQuote: WizardQuote: Ace2You roll a six-sided die thirty times. Whatís the probability you donít roll any consecutive fives?
Only closed-form solutions are beer-worthy
link to original post
I used a Markov chain to get 107,932,636,085,236,000,000,000 / 221,073,919,720,733,000,000,000 =~ 0.48821967. Note I was rebuffed my Excel's limit of 15 significant digits. I can explain the method in more detail upon request, but it was quite easy in Excel.
Hopefully I will get partial credit.
link to original post
Quote: Ace2You roll a six-sided die thirty times. Whatís the probability you donít roll any consecutive fives?
Only closed-form solutions are beer-worthy
link to original post
If you look at the probabilities of no consecutive fives in 6^n permutations (6,35,205,1200, 7025Ö), itís easy to see that, starting with the third term, each term of the series is the sum of two previous terms times five (so 1200 = (35 + 205)5). So itís similar to Fibonacci and the 30th term of the series divided by 6^30 will give you the answer, though thatís not exactly closed-form
The spacing of the Fibonacci series trends towards the golden ratio Φ. Φ is obtained by applying the quadratic formula using a,b,c values of 1,-1,-1 to get (1+5^.5)/2. For large n, the nth term of the Fibonacci series can be calculated (simplified formula) by taking Φ^n / 5^.5
The Fibonacci series corresponds to the probabilities of no consecutive successes for a 50/50 event like a coin flip. Since we are rolling a die (1:5 event), we plug a,b,c values of 1, -5, -5 into the quadratic formula to get the spacing ratio s of (5 + 45^.5) / 2. With that we can directly calculate the answer of:
s^(30+2) / (5 * 45^.5 * 6^30) =~0.48821967 chance of no consecutive fives in thirty rolls
Footnote: 30 rolls is close to the exact median, which could be estimated by taking the average number of rolls to get consecutive fives (6 + 6^2 =42) times Ln(2) =~29.1
Quote: Ace2If you look at the probabilities of no consecutive fives in 6^n permutations (6,35,205,1200, 7025Ö), itís easy to see that, starting with the third term, each term of the series is the sum of two previous terms times five (so 1200 = (35 + 205)5). So itís similar to Fibonacci and the 30th term of the series divided by 6^30 will give you the answer, though thatís not exactly closed-form
link to original post
Actually, pretty much any Fibonacci sequence can be converted to closed-form, using matrix algebra; in this case:
[ f(n+1) ] [ 5 5 ] [ f(n) ]
[ ] = [ ] [ ]
[ f(n) ] [ 1 0 ] [ f(n-1) ]
where f(0) = 1 and f(1) = 6 (f(0) = 1 since 5 f(0) = f(2) - 5 f(1) = 35 - 5 x 6)
The closed form for the Nth term is (deep inhale):
2 sqrt(5) / 5 x ( ((5 + 3 sqrt(5)) / 2)^N - ((5 - 3 sqrt(5)) / 2)^N ) + sqrt(5) / 15 x ( (3 sqrt(5) - 5)/2 x ((5 + 3 sqrt(5)) / 2)^N + (3 sqrt(5) + 5)/2 x ((5 - 3 sqrt(5)) / 2)^N )
Let f(0) and f(1) be given, and f(n) = a f(n-1) + b f(n-2)
Note that if you are given f(1) and f(2), f(2) = a f(1) + b f(0), so f(0) = (f(2) - a f(1)) / b
Assume a and b are positive, so the Eigenvalues are real and distinct
| a b |
| | results in Eigenvalues (a / 2 +/- sqrt(a^2 + 4b) / 2)
| 1 0 |
[x]
In each case, given Eigenvalue x, the corresponding Eigenvector is [ ], since:
[1]
[a - x b] [x] [ax - x^2 + b] [-(x^2 - ax - b)] [0]
[ ] [ ] = [ ] = [ ] = [ ]
[1 -x] [1] [ 0 ] [ 0 ] [0]
[f(n+1)] [ a b ] [ f(n) ] [f(n+1)] [ a b ]^n [f(1)]
[ ] [ ] [ ] = [ ] [ ] [ ]
[ f(n) ] [ 1 0 ] [f(n-1)] [ f(n) ] [ 1 0 ] [f(0)]
Let p and q be the Eigenvalues:
[a b]^n [p q] [p^n 0 ] [p q]^(-1)
[ ] = [ ] [ ] [ ]
[1 0] [1 1] [ 0 q^n] [1 1]
[a b]^n [p q] [p^n 0 ] 1 [1 -q]
[ ] = [ ] [ ] x ----- [ ]
[1 0] [1 1] [ 0 q^n] p - q [-1 p]
We are only interested in the bottom row, since we are only interested in f(n):
1 [# #] [1 -q]
= ----- [ ] [ ]
p - q [p^n q^n] [-1 p]
1 [# #]
= ----- [ ]
p - q [p^n - q^n -q p^n + p q^n]
[f(n+1)] 1 [# #] [f(1)]
[ ] = ----- [ ] [ ]
[ f(n) ] p - q [p^n - q^n p q^n - q p^n] [f(0)]
f(n) = ((p^n - q^n) f(1) + (p q^n - q p^n) f(0)) / (p - q)
where p = a / 2 + sqrt(a^2 + 4b) / 2 and q = a / 2 - sqrt(a^2 + 4b) / 2
Direct: https://www.youtube.com/watch?v=ITSbuT9ojOw
By the way, this was hardly an Easy math puzzle.

What is the area of the yellow square?
I get
Dog Hand
To make the maths easier, let the rectangle have a width of 12x and height 24x. (These are picked so it's easier to work out 3/4 or 4/3 of them). Then the width of the lower trangle is 3/4 of its height, so is 24x*3/4 = 18x; and the height of the top triangle is 12x*4/3 = 16x.
One observes that the total height of 4 is equal to 24x+16x=40x. Also the width of the base is 18x+12x=30x.
Hence the actual height of the rectangle is 2.4.
Thus the square is 2.4 x 2.4; so it's area is 5.76.
(When I was working this out on paper, I did actually use 12x by 24x before I knew the result!)
It is an isosceles triangle, so construct the altitude to create two 3-4-5 right triangles.
If x is the side length of the square, the vertical leg is x and 4 - x, and the horizontal leg is x/2 and 3 - x/2.
The two smaller white triangles are also in 3-4-5 proportion, so the two hypotenuses are 5/3 (3 - x/2) and 4/3 (3 - x):
5/3 (3 - x/2) + 5/4 (3 - x) = 5
10 - (5/6 x + 5/4) x = 5
The side length of the square is 12/5, so its area is 144 / 25


