Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
April 25th, 2021 at 10:02:24 PM
permalink
Quote: WizardI want to phrase it in a way that there is only one reasonable answer. That is why I added wordage about it being a round trip.
Fair enough, then go back to your original wording with "cross" and "return trip". But even still, my recent comment applies, the question in last line needs to be the Names of the cities, not A and B.....(those are the ships).
April 26th, 2021 at 5:09:03 AM
permalink
I asked Ace about the two-dice case in my spoiler. To be specific, two players roll two dice each. What is the probability they roll the same thing?
For full praise and glory, what is the answer for the five dice case?
11/216
For full praise and glory, what is the answer for the five dice case?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
April 26th, 2021 at 7:44:41 AM
permalink
Revised answer : 384,156 / 6^10 =~ 1 in 157.
In my first answer I had divided by 6^12, so it was off by a factor of 6^2.
In my first answer I had divided by 6^12, so it was off by a factor of 6^2.
It’s all about making that GTA
April 26th, 2021 at 7:47:08 AM
permalink
Quote: WizardFive red dice and five blue dice are rolled. What is the probability the two rolls are the same, disregarding the order the dice are thrown?
Solved with brute force.
Of ther 7776 ways to roll the five red dice:
(a) 6 are five of a kind; there is 1 matching roll of the blue dice
(b) 150 are four of a kind (e.g. 11112); there are 5 matching rolls of the blue dice (each of the 5 dice can be the 2)
(c) 300 are a full house (e.g. 11122); there are 10 matching rolls of the blue dice (there are 10 possible pairs of dice for the 2s)
(d) 1200 are three of a kind (e.g. 11123); there are 20 matching rolls of the blue dice (5 for the lower single die; for each of these, 4 for the higher single die)
(e) 1800 are two pair (e.g. 11223); there are 30 matching rolls of the blue dice (5 for the unpaired die; for each of these, 6 pairs for the lower pair)
(f) 3600 are one pair (e.g. 11234); there are 60 matching rolls of the blue dice (5 for the lowest unpaired die; for each of these, 4 for the middle unpaired die; for each of these, 3 for the highest unpaired die)
(g) 720 are five different numbers (e.g. 12345); there are 120 matching rolls of the blue dice (5 for the lowest, 4 for the second-lowest, and so on)
Of the 7776 x 7776 ways to roll the 10 dice, there are (6 x 1) + (150 x 5) + (300 x 10) + (1200 x 20) + (1800 x 30) + (3600 x 60) + (720 x 120) rolls where the red dice match the blue dice.
This reduces to 3,557 / 559,872, or about 1 / 157.4.
Last edited by: ThatDonGuy on Apr 26, 2021
April 26th, 2021 at 2:48:23 PM
permalink
I agree with Ace and Don. Well done, gentlemen.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 3rd, 2021 at 10:56:18 AM
permalink
From Popular Mechanics...
Kenny, Abby, and Ned got together for a round-robin pickleball tournament, where, as usual, the winner stays on after each game to play the person who sat out that game. At the end of their pickleball afternoon, Abby is exhausted, having played the last seven straight games. Kenny, who is less winded, tallies up the games played:
Kenny played 8 games
Abby played 12 games
Ned played 14 games
Who won the fourth game against whom?
Kenny, Abby, and Ned got together for a round-robin pickleball tournament, where, as usual, the winner stays on after each game to play the person who sat out that game. At the end of their pickleball afternoon, Abby is exhausted, having played the last seven straight games. Kenny, who is less winded, tallies up the games played:
Kenny played 8 games
Abby played 12 games
Ned played 14 games
Who won the fourth game against whom?
Have you tried 22 tonight? I said 22.
May 3rd, 2021 at 11:27:09 AM
permalink
Quote: GialmereWho won the fourth game against whom?
Ned beat Kenny
I will explain my answer if I'm right.
p.s. Stay out of the kitchen!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 3rd, 2021 at 12:02:06 PM
permalink
Quote: WizardNed beat Kenny
I will explain my answer if I'm right.
p.s. Stay out of the kitchen!
Correct!
-----------------------------------
The sport is so new that there's little humor written about it. It's easier to find jokes about it's predecessor, Cucumber Ball.
Have you tried 22 tonight? I said 22.
May 3rd, 2021 at 1:18:35 PM
permalink
Quote: GialmereWho won the fourth game against whom?
Since each game consists of two players, a total of (14 + 12 + 8) / 2 = 17 games were played.
Abby won games 11 through 16, but did not win game 10, so she sat out game 10, as otherwise she would have lost game 10 and not played in game 11 as a result.
Since Abby sat out game 10, she lost game 9.
Kenny and Ned played game 10 and alternated the final seven games, so one played five of the last eight games (sitting out three) and the other played four (sitting out four).
Ned sat out a total of three games, so he played five of the last eight as well as all of the first nine. This means Abby and Ken alternated the first nine games, which were all won by Ned; since Abby played game 9, Ken played game 4.
Game 1: Ned beat Abby
Game 2: Ned beat Ken
Game 3: Ned beat Abby
Game 4: Ned beat Ken
Game 5: Ned beat Abby
Game 6: Ned beat Ken
Game 7: Ned beat Abby
Game 8: Ned beat Ken
Game 9: Ned beat Abby
Game 10: Ned beat Ken
Game 11: Abby beat Ned
Game 12: Abby beat Ken
Game 13: Abby beat Ned
Game 14: Abby beat Ken
Game 15: Abby beat Ned
Game 16: Abby beat Ken
Game 17: Abby played Ned (winner undetermined)
Why, yes, Ken did go 0-8, didn't he?
May 3rd, 2021 at 2:13:17 PM
permalink
The total number of games is 17 (14+12+8)/2.
I got it by then considering that if Abby played the last 7 then she only played 5 of the first 10, so one of the other two won at least 9 of them. This can't be Kenny. So Ned played the first 10, won 10th and played, and lost, the 11th 13th 15th and 17th. So Ned beat Kenny on the 10th. Hence Ned beat Kenny on the 2nd 4th 6th and 8th as well.
Another way to the solution is to realise that Kenny only played 8 games, so never won a match. A loser plays every alternate match, so must have played all the even numbered matches. The above logic suggests Ned won the early matches.
Both of these say Ned beat Kenny in 4th match.
I got it by then considering that if Abby played the last 7 then she only played 5 of the first 10, so one of the other two won at least 9 of them. This can't be Kenny. So Ned played the first 10, won 10th and played, and lost, the 11th 13th 15th and 17th. So Ned beat Kenny on the 10th. Hence Ned beat Kenny on the 2nd 4th 6th and 8th as well.
Another way to the solution is to realise that Kenny only played 8 games, so never won a match. A loser plays every alternate match, so must have played all the even numbered matches. The above logic suggests Ned won the early matches.
Both of these say Ned beat Kenny in 4th match.
May 3rd, 2021 at 2:50:31 PM
permalink
Late to this puzzle but:
There were 17 matches, because (14+12+8)/2 = 17
If Kenny only won 8 matches, then he must have lost every match, because a loser will play in alternate matches.
Kenny must have sat out match #1 and then played and lost in all even numbered matches, if he had played in odd number matches he would have played in 9 matches.
Thus Kenny lost the 4th match.
Abby won the last 7 matches but only played in 5 of the first ten, thus she lost her 5 matches (which were all odd numbered matches.)
Norman played in 14 matches, he can only have played in a maximum of 4 of the last seven matches, all of which Abby won. Thus he played in all 10 of the first 10 matches, winning them all.
So, in the 4th match, Norman beat Kenny.
There were 17 matches, because (14+12+8)/2 = 17
If Kenny only won 8 matches, then he must have lost every match, because a loser will play in alternate matches.
Kenny must have sat out match #1 and then played and lost in all even numbered matches, if he had played in odd number matches he would have played in 9 matches.
Thus Kenny lost the 4th match.
Abby won the last 7 matches but only played in 5 of the first ten, thus she lost her 5 matches (which were all odd numbered matches.)
Norman played in 14 matches, he can only have played in a maximum of 4 of the last seven matches, all of which Abby won. Thus he played in all 10 of the first 10 matches, winning them all.
So, in the 4th match, Norman beat Kenny.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
May 3rd, 2021 at 8:31:50 PM
permalink
I’m sure everyone is familiar with the St Petersburg paradox. If you get paid 2^x dollars the first time heads appears in a series of x coin flips, the EV is infinity.
I’ve noticed that the EV is finite for if you substitute any value less than e^.5 (about 1.65) for 2. Can someone explain why e^.5 is the upper limit for a finite EV?
I’ve noticed that the EV is finite for if you substitute any value less than e^.5 (about 1.65) for 2. Can someone explain why e^.5 is the upper limit for a finite EV?
It’s all about making that GTA
May 4th, 2021 at 8:26:32 AM
permalink
Quote: Ace2I’m sure everyone is familiar with the St Petersburg paradox. If you get paid 2^x dollars the first time heads appears in a series of x coin flips, the EV is infinity.
I’ve noticed that the EV is finite for if you substitute any value less than e^.5 (about 1.65) for 2. Can someone explain why e^.5 is the upper limit for a finite EV?
It's not. The EV for any positive value n < 2 is n / (2 - n).
Let a be the number in place of 2 - i.e. you get a^n dollars if the first head appears on the nth toss.
The value = 1/2 x a + 1/4 + a^2 + 1/8 x a^3 + 1/16 x a^4 + ...
= a/2 + (a/2)^2 + (a/2)^3 + (a/2)^4 + ...
= a/2 (1 + a/2 + (a/2)^2 + a/2)^3 + ...)
If a >= 2, then a/2 >= 1, and the sum diverges.
If a < 2, then a/2 < 1, and the sum is 1 / (1 - a/2), so the value = (a/2) / (1 - a/2) = a / (2 - a).
Last edited by: ThatDonGuy on May 4, 2021
May 4th, 2021 at 4:53:27 PM
permalink
I used the integral from zero to infinity of .5 * e^(-x/2) * a^x. For a values under 1.2, it comes out quite close to a / (2 - a). But apparently my answer is for the exponential distribution only and does not carry over to the binomial (it usually does). I thought this would work...maybe the Wizard can explain why it doesn’t?Quote: ThatDonGuyIt's not. The EV for any positive value n < 2 is n / (2 - n).
Let a be the number in place of 2 - i.e. you get a^n dollars if the first head appears on the nth toss.
The value = 1/2 x a + 1/4 + a^2 + 1/8 x a^3 + 1/16 x a^4 + ...
= a/2 + (a/2)^2 + (a/2)^3 + (a/2)^4 + ...
= a/2 (1 + a/2 + (a/2)^2 + a/2)^3 + ...)
If a >= 2, then a/2 >= 1, and the sum diverges.
If a < 2, then a/2 < 1, and the sum is 1 / (1 - a/2), so the value = (a/2) / (1 - a/2) = a / (2 - a).
It’s all about making that GTA
May 5th, 2021 at 5:39:44 PM
permalink
Here's an easy one similar to the pickleball puzzle...
Adam and Eve play rock-paper-scissors 10 times. You know that:
Adam uses rock three times, scissors six times, and paper once.
Eve uses rock twice, scissors four times, and paper four times.
There are no ties in all 10 games.
The order of games is unknown.
Who wins? By how much?
Adam and Eve play rock-paper-scissors 10 times. You know that:
Adam uses rock three times, scissors six times, and paper once.
Eve uses rock twice, scissors four times, and paper four times.
There are no ties in all 10 games.
The order of games is unknown.
Who wins? By how much?
Have you tried 22 tonight? I said 22.
May 5th, 2021 at 6:40:14 PM
permalink
Quote: GialmereHere's an easy one similar to the pickleball puzzle...
Adam and Eve play rock-paper-scissors 10 times. You know that:
Adam uses rock three times, scissors six times, and paper once.
Eve uses rock twice, scissors four times, and paper four times.
There are no ties in all 10 games.
The order of games is unknown.
Who wins? By how much?
Eve uses scissors four times. Since there are no ties, they have to be the four times Adam did not use scissors.
The breakdown is:
Adam uses scissors, Eve uses rock: 2 times (Eve wins)
Adam uses scissors, Eve uses paper: 4 times (Adam wins)
Adam uses rock, Eve uses scissors: 3 times (Adam wins)
Adam uses paper, Eve uses scissors: 1 time (Eve wins)
Adam wins 7 games; Eve wins 3
May 5th, 2021 at 9:27:15 PM
permalink
Quote: ThatDonGuy
Eve uses scissors four times. Since there are no ties, they have to be the four times Adam did not use scissors.
The breakdown is:
Adam uses scissors, Eve uses rock: 2 times (Eve wins)
Adam uses scissors, Eve uses paper: 4 times (Adam wins)
Adam uses rock, Eve uses scissors: 3 times (Adam wins)
Adam uses paper, Eve uses scissors: 1 time (Eve wins)
Adam wins 7 games; Eve wins 3
Correct!
-----------------------------------------
"Mom, how did humans come to exist?"
"Well, you see, God created Adam and Eve..."
"But dad said we came from apes."
"He was talking about his side of the family, I'm telling you about mine."
Have you tried 22 tonight? I said 22.
May 6th, 2021 at 9:43:08 AM
permalink
Speaking of Adam and Eve... why does Eve have a navel?
Dog Hand
May 8th, 2021 at 6:45:57 AM
permalink
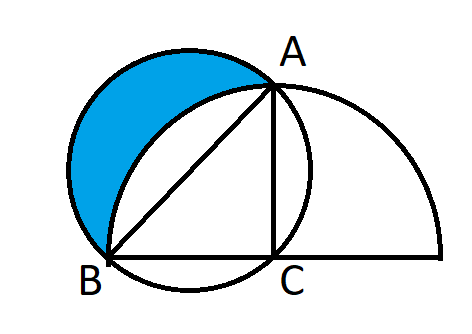
BC = AC = 1
ACB is a right angle.
What is the area of the blue region?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 8th, 2021 at 7:08:00 AM
permalink
Quote: Wizard
BC = AC = 1
ACB is a right angle.
What is the area of the blue region?
The area of the blue region = (1/2 the area of the circle with diameter AB) + (the area of triangle ACB) - (1/4 the area of the circle with radius AB)
= 1/2 x PI x (sqrt(2) / 2)^2 + 1/2 x 1 x 1 - 1/4 x PI x 1^2
= PI / 4 + 1/2 - PI / 4 = 1/2
May 8th, 2021 at 8:00:24 AM
permalink
Quote: Wizard
BC = AC = 1
ACB is a right angle.
What is the area of the blue region?
I get
Area = 1/2
Right triangle ACB has area 1/2*base*height = 1/2, and the length of AB is sqrt(2).
Since AC and BC are both chords of the circle ACB (I mean the circle with points A, C, and B on its circumference), their perpendicular bisectors meet at the center of circle ACB, which is the midpoint of AB. Thus, AB is the diameter of circle ACB. This means the area of circle ACB is pi*(length AB)^2/4 = pi/2. This means
Area of the half-circle ACB is pi/4.
A and B are also points on a big half-circle with C at its center and, thus, a radius of 1, so
Area of the quarter-big-circle is 1/4*pi*radius^2 = pi/4.
Let's let E be the unknown area, and D be the area between E and the line AB. The area of D is then the difference between the area of the quarter-big-circle ACB and the area of the right triangle ACB:
Area of D = pi/4 - 1/2
Finally, the area of E is the difference between the area of the half-circle ACB and the area of D:
Area of E = pi/4 - (pi/4 - 1/2) = 1/2.
Right triangle ACB has area 1/2*base*height = 1/2, and the length of AB is sqrt(2).
Since AC and BC are both chords of the circle ACB (I mean the circle with points A, C, and B on its circumference), their perpendicular bisectors meet at the center of circle ACB, which is the midpoint of AB. Thus, AB is the diameter of circle ACB. This means the area of circle ACB is pi*(length AB)^2/4 = pi/2. This means
Area of the half-circle ACB is pi/4.
A and B are also points on a big half-circle with C at its center and, thus, a radius of 1, so
Area of the quarter-big-circle is 1/4*pi*radius^2 = pi/4.
Let's let E be the unknown area, and D be the area between E and the line AB. The area of D is then the difference between the area of the quarter-big-circle ACB and the area of the right triangle ACB:
Area of D = pi/4 - 1/2
Finally, the area of E is the difference between the area of the half-circle ACB and the area of D:
Area of E = pi/4 - (pi/4 - 1/2) = 1/2.
Dog Hand
May 8th, 2021 at 8:29:13 AM
permalink
Imagine a point D on the outer semi-circle, so that there is a circle ACBD. The diameter, AB = SQRT(AC2+AB2) = SQRT(1+1) = SQRT(2). Thus the area of all the circle is Pi r2=Pi/2. So the semi circle ABD is Pi/4.
The area of the quarter circle ACB is also Pi/4 (as r=1, AC=CB=1).
Consider the area of the shape = triangle(ACB)+semicircle(ABD) = 1/2 + Pi/4 (the former is half the unit square).
But the shape is also the unknown area + quartercircle(ACB) = x + Pi/4.
So the unknown area x = 1/2.
The area of the quarter circle ACB is also Pi/4 (as r=1, AC=CB=1).
Consider the area of the shape = triangle(ACB)+semicircle(ABD) = 1/2 + Pi/4 (the former is half the unit square).
But the shape is also the unknown area + quartercircle(ACB) = x + Pi/4.
So the unknown area x = 1/2.
May 8th, 2021 at 2:14:57 PM
permalink
Congratulations to Charlie, Dog, and Don -- I agree.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 10th, 2021 at 8:01:24 AM
permalink
It's easy Monday. Let's play chess...
In a chess tournament, each contestant plays a match against every other contestant. Each contestant gets 1 point for every match he wins, 0.5 points for every tied match, and 0 for every game he loses.
At the end of the tournament, it is seen that all competitors got a different number of points and the last competitor in the score ranking defeated each of the top three competitors.
Accordingly, what is the minimum number of competitors participating in the tournament?
In a chess tournament, each contestant plays a match against every other contestant. Each contestant gets 1 point for every match he wins, 0.5 points for every tied match, and 0 for every game he loses.
At the end of the tournament, it is seen that all competitors got a different number of points and the last competitor in the score ranking defeated each of the top three competitors.
Accordingly, what is the minimum number of competitors participating in the tournament?
Have you tried 22 tonight? I said 22.
May 10th, 2021 at 8:32:57 AM
permalink
I'm guessing 13 players...
The lowest placed person scored three wins so got 3 points. Next place up could have got 3 1/2 points and it continues.
So the scores, from the bottom, are at a minimum 3 3.5 4 4.5 5 etc. Thus the winning total is at least (3+(N-1)/2), and the average is 3+(N-1)/4, so the minimum total of all scores is 3N+(N-1)N/4.
Also each match creates a score of 1, so the total of all scores is N(N-1)/2.
For these to be equal N(N-1)/2 = 3N + (N-1)N/4 or N(N-1)/4 = 3N or (N-1)/4 = 3 or N=13.
So the scores are 9 8.5 8 7.5 7 6.5 6 5.5 5 4.5 4 3.5 3 and this equals the total number of matches.
The lowest placed person scored three wins so got 3 points. Next place up could have got 3 1/2 points and it continues.
So the scores, from the bottom, are at a minimum 3 3.5 4 4.5 5 etc. Thus the winning total is at least (3+(N-1)/2), and the average is 3+(N-1)/4, so the minimum total of all scores is 3N+(N-1)N/4.
Also each match creates a score of 1, so the total of all scores is N(N-1)/2.
For these to be equal N(N-1)/2 = 3N + (N-1)N/4 or N(N-1)/4 = 3N or (N-1)/4 = 3 or N=13.
So the scores are 9 8.5 8 7.5 7 6.5 6 5.5 5 4.5 4 3.5 3 and this equals the total number of matches.
May 10th, 2021 at 11:21:53 AM
permalink
I get 13 as well.
Let's call the number of players n.
I figure the last place player has only three wins, against the top 3 players, and lost every other game. That gives him 3 points.
I then figure every subsequent player in order of points as 0.5 more points than the previous one, in rank. That would give the highest ranking player 3+(n-1)/2 points.
Taking the sum of 3 to 3+(n-1)/2, by a 1/2 point per step gives us (((n+5)*(n+6)/2)-15)/2
The total games played with n players is n*(n-1)/2, where everybody players everybody else, once. Each game results in one total point, to that is also the total points earned among all players.
Then solve for n:
(((n+5)*(n+6)/2)-15)/2 = n*(n-1)/2
((n+5)*(n+6)/2)-15 = n*(n-1)
(n+5)*(n+6)/2 = n*(n-1) + 15
(n+5)*(n+6) = 2*n*(n-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
n^2 + 11n = 2n^2 - 2n
n + 11 = 2n-2
n=13
There should be a way to arrange the wins and losses to achieve the desired goal.
In fact, here a way! The body of the player shows the winning player number. T=tie. I'm pretty sure there are other solutions.
Last edited by: Wizard on May 10, 2021
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 10th, 2021 at 5:12:00 PM
permalink
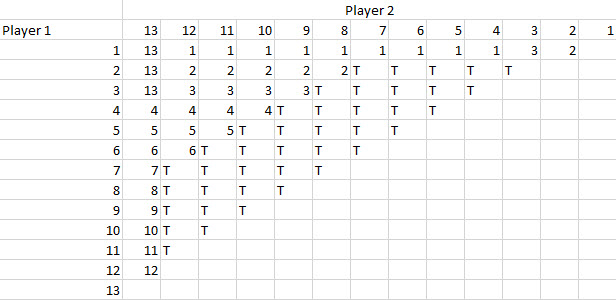
Quote: charliepatrickI'm guessing 13 players...
The lowest placed person scored three wins so got 3 points. Next place up could have got 3 1/2 points and it continues.
So the scores, from the bottom, are at a minimum 3 3.5 4 4.5 5 etc. Thus the winning total is at least (3+(N-1)/2), and the average is 3+(N-1)/4, so the minimum total of all scores is 3N+(N-1)N/4.
Also each match creates a score of 1, so the total of all scores is N(N-1)/2.
For these to be equal N(N-1)/2 = 3N + (N-1)N/4 or N(N-1)/4 = 3N or (N-1)/4 = 3 or N=13.
So the scores are 9 8.5 8 7.5 7 6.5 6 5.5 5 4.5 4 3.5 3 and this equals the total number of matches.
Quote: Wizard
I get 13 as well.
[Note: The Wizard's full response cannot be quoted. An inadvertent scripting bug created by all the parentheses perhaps?]
Correct!
Very good.
-----------------------------------------
Have you tried 22 tonight? I said 22.
May 11th, 2021 at 6:18:19 AM
permalink
This is not a math puzzle per say, but more of a logic/programming question.
Let's say I have an array of a bunch of numbers. I want to print out every possible order of said numbers. What is an algorithm for a way to arrange said list in all n! possible way, where n is the size of the array? I'm looking to both minimize computer code and computer operations.
Thank you!
Let's say I have an array of a bunch of numbers. I want to print out every possible order of said numbers. What is an algorithm for a way to arrange said list in all n! possible way, where n is the size of the array? I'm looking to both minimize computer code and computer operations.
Thank you!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 11th, 2021 at 9:46:01 AM
permalink
Do you care whether two of the numbers in the array are identical, such that some of the permutations are not unique?
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
May 11th, 2021 at 9:46:04 AM
permalink
Do you care whether two of the numbers in the array are identical, such that some of the permutations are not unique?
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
May 11th, 2021 at 9:46:07 AM
permalink
Do you care whether two of the numbers in the array are identical, such that some of the permutations are not unique?
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
May 11th, 2021 at 9:54:45 AM
permalink
Note: When I paste in the source code below as text, and then click the PREVIEW button, the server gives me the following error:
Forbidden
You don't have permission to access this resource.
Thus, to get around that, I'll make a screenshot of my code.
Note that is isn't just an algorithm, but actual Excel VBA code. I suspect I could turn it into a general algorithm for all languages if need be. Also note that instead of an array of numbers, for convenience I used a string of numbers.
It seems to be producing the correct results for all size strings. It did take about ten seconds or so on my slow system, with a string length of 9. String lengths of 7 or less are produced instantly.
Change the aa$ = "12345" to test your own string.
Forbidden
You don't have permission to access this resource.
Thus, to get around that, I'll make a screenshot of my code.
Note that is isn't just an algorithm, but actual Excel VBA code. I suspect I could turn it into a general algorithm for all languages if need be. Also note that instead of an array of numbers, for convenience I used a string of numbers.
It seems to be producing the correct results for all size strings. It did take about ten seconds or so on my slow system, with a string length of 9. String lengths of 7 or less are produced instantly.
Change the aa$ = "12345" to test your own string.
May 11th, 2021 at 10:30:11 AM
permalink
Quote: EdCollinsNote: When I paste in the source code below as text, and then click the PREVIEW button, the server gives me the following error:
Forbidden
You don't have permission to access this resource.
That's the same message I got when simply trying to quote the Wizard's answer to the previous question. I also note that the forum posts won't come up on the main page.
Something is buggy. Either they're working on the site or it's under attack.
Have you tried 22 tonight? I said 22.
May 11th, 2021 at 11:24:37 AM
permalink
Here’s my unconventional puzzle of the day.
Let’s say you and your buddy want to shoot some dice at home at $100 per bet. Your friend plays the pass line and you have the other side of the bet.
Can you think of a simple way, without modifying the game much, to adjust the house edge to exactly zero?
For instance, if you made a rule that when a 2 is rolled on a come out roll (craps) the pass line loses only half the money wagered, that would bring the house edge down to just 2.5 basis points. Very close to zero but not zero
Let’s say you and your buddy want to shoot some dice at home at $100 per bet. Your friend plays the pass line and you have the other side of the bet.
Can you think of a simple way, without modifying the game much, to adjust the house edge to exactly zero?
For instance, if you made a rule that when a 2 is rolled on a come out roll (craps) the pass line loses only half the money wagered, that would bring the house edge down to just 2.5 basis points. Very close to zero but not zero
It’s all about making that GTA
May 11th, 2021 at 5:18:42 PM
permalink
I'm working on an easier solution, but I think I have one for the pass - well, sort of; it only works with bets that are even numbers
A missed point of 6, 8, or 10 pushes
A 6-1 on the comeout pushes
A missed point of 5 loses half
A missed point of 9 where the comeout was 6-3 (instead of 5-4) loses half
A missed point of 6, 8, or 10 pushes
A 6-1 on the comeout pushes
A missed point of 5 loses half
A missed point of 9 where the comeout was 6-3 (instead of 5-4) loses half
May 11th, 2021 at 6:02:34 PM
permalink
Quote: ThatDonGuyI'm working on an easier solution, but I think I have one for the pass - well, sort of; it only works with bets that are even numbers
A missed point of 6, 8, or 10 pushes
A 6-1 on the comeout pushes
A missed point of 5 loses half
A missed point of 9 where the comeout was 6-3 (instead of 5-4) loses half
That’s complicated. I found a simple but unsatisfying one:
Making a point with a hard 6 or hard 8 pays an extra 56%
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
May 11th, 2021 at 6:31:05 PM
permalink
Getting back to my sort question, what I was looking for is called Heap's Algorithm. It's rather hard to explain without using computer code. Here is my best effort to put it in simple English to see every permutation and get back to the starting one.
With two items: switch them twice
With three items: alternate switching (1) first and second and (2) first and third -- three times
With n items, where n is even and >=4:
1. Do procedure for n-1 items, leaving 4th alone.
2. Switch 1st and nth item.
3. Repeat step 1
4. Switch 2nd and nth item:
5. Repeat step 1
4. Switch 3rd and nth item:
5. Repeat step 1
6. Keep repeating this process until you switch (n-1)th and nth item.
7. Repeat step 1
With n items, where n is odd and >=5:
1. Do procedure for n-1 items, leaving 5th alone.
2. Switch 1st and nth item.
3. Repeat step 1
4. Repeat steps 1 and 2 n-1 more times.
With two items: switch them twice
With three items: alternate switching (1) first and second and (2) first and third -- three times
With n items, where n is even and >=4:
1. Do procedure for n-1 items, leaving 4th alone.
2. Switch 1st and nth item.
3. Repeat step 1
4. Switch 2nd and nth item:
5. Repeat step 1
4. Switch 3rd and nth item:
5. Repeat step 1
6. Keep repeating this process until you switch (n-1)th and nth item.
7. Repeat step 1
With n items, where n is odd and >=5:
1. Do procedure for n-1 items, leaving 5th alone.
2. Switch 1st and nth item.
3. Repeat step 1
4. Repeat steps 1 and 2 n-1 more times.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 11th, 2021 at 7:23:03 PM
permalink
56% is not a feasible payout. Okay, it would be on $100 but it needs to be an easy ratio. Let’s say the min/max bet is $10 / $100Quote: unJonQuote: ThatDonGuyI'm working on an easier solution, but I think I have one for the pass - well, sort of; it only works with bets that are even numbers
A missed point of 6, 8, or 10 pushes
A 6-1 on the comeout pushes
A missed point of 5 loses half
A missed point of 9 where the comeout was 6-3 (instead of 5-4) loses half
That’s complicated. I found a simple but unsatisfying one:Making a point with a hard 6 or hard 8 pays an extra 56%
If any payout ratio is allowed, you could just pay a winning bet at 251 to 244 without changing any rules.
It’s all about making that GTA
May 11th, 2021 at 7:42:01 PM
permalink
Quote: gordonm888Do you care whether two of the numbers in the array are identical, such that some of the permutations are not unique?
Quote: gordonm888Do you care whether two of the numbers in the array are identical, such that some of the permutations are not unique?
Quote: gordonm888Do you care whether two of the numbers in the array are identical, such that some of the permutations are not unique?
gordonm888,
That's a unique way to demonstrate your question ;-)
Dog Hand
May 11th, 2021 at 8:13:12 PM
permalink
Quote: Ace256% is not a feasible payout. Okay, it would be on $100 but it needs to be an easy ratio. Let’s say the min/max bet is $10 / $100Quote: unJonQuote: ThatDonGuyI'm working on an easier solution, but I think I have one for the pass - well, sort of; it only works with bets that are even numbers
A missed point of 6, 8, or 10 pushes
A 6-1 on the comeout pushes
A missed point of 5 loses half
A missed point of 9 where the comeout was 6-3 (instead of 5-4) loses half
That’s complicated. I found a simple but unsatisfying one:Making a point with a hard 6 or hard 8 pays an extra 56%
If any payout ratio is allowed, you could just pay a winning bet at 251 to 244 without changing any rules.
I said it was unsatisfying.
Here’s another way;
pay true odds on the point so 4/10 pays 2:1, 5/9 pays 3:2 and 6/8 pays 6:5. But a come out seven pushes if it’s a 6/1 or 2/5.
So that’s an edge less come out and an edge less point.
So that’s an edge less come out and an edge less point.
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
May 11th, 2021 at 8:39:52 PM
permalink
Quote: DogHandgordonm888,
That's a unique way to demonstrate your question ;-)
Dog Hand
LOL, I had no idea it triple-posted. Maybe we can all catch up to EvenBob if the site remains buggy.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
May 12th, 2021 at 8:06:40 AM
permalink
Quote: Ace256% is not a feasible payout. Okay, it would be on $100 but it needs to be an easy ratio. Let’s say the min/max bet is $10 / $100Quote: unJonQuote: ThatDonGuyI'm working on an easier solution, but I think I have one for the pass - well, sort of; it only works with bets that are even numbers
A missed point of 6, 8, or 10 pushes
A 6-1 on the comeout pushes
A missed point of 5 loses half
A missed point of 9 where the comeout was 6-3 (instead of 5-4) loses half
That’s complicated. I found a simple but unsatisfying one:Making a point with a hard 6 or hard 8 pays an extra 56%
If any payout ratio is allowed, you could just pay a winning bet at 251 to 244 without changing any rules.
I don't think a solution is possible (at least, not on the pass side) without any sort of fractional bet payout.
Here is a table of probabilities of results broken down by comeout roll and resolution roll; the numbers are the probabilities multiplied by (36 x 495); the losing results for pass are negative numbers.
For example, the probability that the comeout is 3,1 and the result is a 7 is 660/(36 x 495), and the probability that the comeout is 4,4 and the point is also made the hard way is 45/(36 x 495).
"N/A" means that the result is not applicable as it was resolved on the comeout.
The sum is -252, so in order to make the house advantage zero, one or more of the results needs to be modified to increase their values by a total of 252. This is not easy to do when you notice that each number is a multiple of 55, 90, or 198. If you allow half-losses, these become 55, 45, and 99.
For Don't Pass, change all of the signs and replace the -495 in the last row with zero; the sum becomes -243. (To make it easier, leave the values as they are, except for the last row; the sum now needs to be reduced by 243.)
| Comeout | Point 1 | Point 2 | Point 3 | 7 | ||||
|---|---|---|---|---|---|---|---|---|
| 1,1 | N/A | -495 | ||||||
| 2,1 | N/A | -990 | ||||||
| 3,1 | 3,1 | 220 | 2,2 | 110 | 7 | -660 | ||
| 2,2 | 3,1 | 110 | 2,2 | 55 | 7 | -330 | ||
| 4,1 | 4,1 | 198 | 3,2 | 198 | 7 | -594 | ||
| 3,2 | 4,1 | 198 | 3,2 | 198 | 7 | -594 | ||
| 5,1 | 5,1 | 180 | 4,2 | 180 | 3,3 | 90 | 7 | -540 |
| 4,2 | 5,1 | 180 | 4,2 | 180 | 3,3 | 90 | 7 | -540 |
| 3,3 | 5,1 | 90 | 4,2 | 90 | 3,3 | 45 | 7 | -270 |
| 6,1 | N/A | 990 | ||||||
| 5,2 | N/A | 990 | ||||||
| 4,3 | N/A | 990 | ||||||
| 6,2 | 6,2 | 180 | 5,3 | 180 | 4,4 | 90 | 7 | -540 |
| 5,3 | 6,2 | 180 | 5,3 | 180 | 4,4 | 90 | 7 | -540 |
| 4,4 | 6,2 | 90 | 5,3 | 90 | 4,4 | 45 | 7 | -270 |
| 6,3 | 6,3 | 198 | 5,4 | 198 | 7 | -594 | ||
| 5,4 | 6,3 | 198 | 5,4 | 198 | 7 | -594 | ||
| 6,4 | 6,4 | 220 | 5,5 | 110 | 7 | -660 | ||
| 5,5 | 6,4 | 110 | 5,5 | 55 | 7 | -330 | ||
| 6,5 | N/A | 990 | ||||||
| 6,6 | N/A | -495 |
May 12th, 2021 at 8:53:37 AM
permalink
Here’s an idea
If the shooter wins with a point of 5 (must be with a 1,4 combination), then he rolls for a bonus as follows:.
If he rolls a 4, then he gets paid a bonus of seven times his original wager and the round is over. If he rolls a 10, then he rolls again. If he rolls any other number then he gets no bonus and the round is over.
1/9 chance of establishing a point of 5 times 1/5 of winning it (with 1,4) times 1/11 chance of winning the bonus is 1/495. Paid at 7x will eliminate the edge of 7/495
Adding a bonus round isn’t ideal but...it only lasts an average of 1.09 rolls, it only occurs once every 45 resolutions and the original game/payout isn’t changed at all
After running through numbers in my head I tend to agree with Don that there probably isn’t a way to eliminate the edge exactly using just the original game and “reasonable” fractional payout adjustments like 1/2. In a real world scenario I think my original proposal of the craps-2 losing only half is probably the best solution. Easy to understand, no material effect on variance and and edge of 2.5 basis points is essentially zero...that’s less than the edge difference between pass and DP
If the shooter wins with a point of 5 (must be with a 1,4 combination), then he rolls for a bonus as follows:.
If he rolls a 4, then he gets paid a bonus of seven times his original wager and the round is over. If he rolls a 10, then he rolls again. If he rolls any other number then he gets no bonus and the round is over.
1/9 chance of establishing a point of 5 times 1/5 of winning it (with 1,4) times 1/11 chance of winning the bonus is 1/495. Paid at 7x will eliminate the edge of 7/495
Adding a bonus round isn’t ideal but...it only lasts an average of 1.09 rolls, it only occurs once every 45 resolutions and the original game/payout isn’t changed at all
After running through numbers in my head I tend to agree with Don that there probably isn’t a way to eliminate the edge exactly using just the original game and “reasonable” fractional payout adjustments like 1/2. In a real world scenario I think my original proposal of the craps-2 losing only half is probably the best solution. Easy to understand, no material effect on variance and and edge of 2.5 basis points is essentially zero...that’s less than the edge difference between pass and DP
Last edited by: Ace2 on May 12, 2021
It’s all about making that GTA
May 12th, 2021 at 9:26:24 AM
permalink
Quote: Ace2Here’s an idea
If the shooter wins with a point of 5 (must be with a 1,4 combination), then he rolls for a bonus as follows:.
If he rolls a 4, then he gets paid a bonus of seven times his original wager and the round is over. If he rolls a 10, then he rolls again. If he rolls any other number then he gets no bonus and the round is over.
1/9 chance of establishing a point of 5 times 1/5 of winning it (with 1,4) times 1/11 chance of winning the bonus is 1/495. Paid at 7x will eliminate the edge of 7/495
Adding a bonus round isn’t ideal but...it only lasts an average of 1.09 rolls, it only occurs once every 45 resolutions and the original game/payout isn’t changed at all
After running through numbers in my head I tend to agree with Don that there probably isn’t a way to eliminate the edge exactly using just the original game and “reasonable” fractional payout adjustments like 1/2. In a real world scenario I think my original proposal of the craps-2 losing only half is probably the best solution. Easy to understand, no material effect on variance and and edge of 2.5 basis points is effectively zero...less than the edge difference between pass and DP
Ran out of time but you can cut off the 11 and a 36 by saying the come out is a hard 8 and it gets made with a hard 8. If that paid 5.6 times bonus we would be edgeless without a bonus roll. Though it’s not an ideal round bonus. If you can work in the 5 to that same roll (so it’s 1/5 as likely) then the bonus could pay a round 28 times.
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
May 12th, 2021 at 9:30:05 AM
permalink
Quote: ThatDonGuy
I don't think a solution is possible (at least, not on the pass side) without any sort of fractional bet payout.
I stand corrected - I found one:
Comeout 12 is a push for both sides (+495)
Point of hardway 8 made hardway is a push (-45)
Point of 6,3 made with 6,3 is a push (-198)
Total adjustment to house edge: +252
Since Pass is now house edge zero, making the rules the same for Don't Pass makes that bet zero HE as well.
May 12th, 2021 at 9:54:30 AM
permalink
Assuming you're only considering the Pass Line Bet. I think one way to do it is when you throw what would be a standoff for Don't Come (say 1-1) then rather than losing you enter a new game to resolve the bet. As per above this happens 495 times and you want to ensure the player only loses 243 units rather than 495. This means that you need a game with one of 55 outcomes, 28 of them the player doesn't lose, 27 of them the player does lose.
It should be fairly easy to use two rolls to create such a game, e.g. Odd followed by not (2,7,12) Even followed by not (2,3,7). Anything else replay the game.
It should be fairly easy to use two rolls to create such a game, e.g. Odd followed by not (2,7,12) Even followed by not (2,3,7). Anything else replay the game.
May 12th, 2021 at 8:42:29 PM
permalink
Passline win is paid at 8:1 instead of 1:1 if:
1) Point is established with easy 6
2) 4 is rolled before winning point and before rolling a 2
3) Point is won with hard 6
1) Point is established with easy 6
2) 4 is rolled before winning point and before rolling a 2
3) Point is won with hard 6
It’s all about making that GTA
May 17th, 2021 at 7:09:15 AM
permalink
It's easy Monday. Let's make a deal...
You're a contestant on "Let's Make A Deal" and confront the famous Monty Hall Problem. You're shown 3 doors and are told that behind one of the doors is a (giant novelty) check worth $10,000. Behind each of the other 2 doors is a goat.
You select door #1.
Monty (who knows which door hides the check and which doors contain zonks) opens door #2 to reveal a goat. He then asks if you want to stay with door #1 or switch to door #3. Should you switch?
Fortunately, you're familiar with game theory and know what to do but, before you can respond, a bell rings. DING! DING! DING! Monty tells you this is now a special zonk redemption round. If you lose the game, you get to play second round except that the check will then be written for $20,000!
Eh? Should you now try to lose round 1 to go for twenty grand in round 2?
As this thought crosses your mind Monty casually adds that if you also lose the second round, you'll play a third round for a check worth $30,000!
You weren't expecting this. Probabilities begin shooting through your head...
What are your best decisions to maximize your potential winnings?
You're a contestant on "Let's Make A Deal" and confront the famous Monty Hall Problem. You're shown 3 doors and are told that behind one of the doors is a (giant novelty) check worth $10,000. Behind each of the other 2 doors is a goat.
You select door #1.
Monty (who knows which door hides the check and which doors contain zonks) opens door #2 to reveal a goat. He then asks if you want to stay with door #1 or switch to door #3. Should you switch?
Fortunately, you're familiar with game theory and know what to do but, before you can respond, a bell rings. DING! DING! DING! Monty tells you this is now a special zonk redemption round. If you lose the game, you get to play second round except that the check will then be written for $20,000!
Eh? Should you now try to lose round 1 to go for twenty grand in round 2?
As this thought crosses your mind Monty casually adds that if you also lose the second round, you'll play a third round for a check worth $30,000!
You weren't expecting this. Probabilities begin shooting through your head...
What are your best decisions to maximize your potential winnings?
Have you tried 22 tonight? I said 22.
May 17th, 2021 at 11:47:54 AM
permalink
If I was on stage, and had to make a decision right then and there, I would NOT switch initially, and hope I did not pick the right door, hoping to win in Round 2 or Round 3.Quote: GialmereWhat are your best decisions to maximize your potential winnings?
And given the opportunity, assuming if I did indeed not pick the right door in Round 1, and thus now advanced to the special zonk Second Round, at that point I think I would switch doors.
If I did not guess right here either, and thus advanced to the 3rd round, I'd definitely switch of course, hoping for the best shot at that final prize of $30,000.
I suspect it's right not to switch in Round 1 and of course you always switch in Round 3. The one round I'm least confident in is the Second Round, but yea, let's switch here too, for the best chance at the $20,000.
