Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Quote: teliotOkay, which leads me to a cute little theorem-ette that is on the slightly non-trivial side (but not that non-trivial), related to the 153 question.
Let N > 0 be any integer. Let S be the sum of the cubes of its digits. Show that the difference (N-S) is always divisible by 3.
For example, N = 1263. S = 1^3 + 2^3 + 6^3 + 3^3 = 1 + 8 + 216 + 27 = 252. N - S = 1011= 3*337.
This is definitely true for every number through 9,999, which I just did in Excel. And late to party but also agree with Charlie results.
Hmmm .... not sure I like the "similar logic will apply" part. Can you formalize that?Quote: charliepatrickWe can split any number into its constituent digits and consider each one in turn. So a number such as 543 look at the difference between 500 and 53, 40 and 43, 3 and 33. If each of these is divisible by 3, then the total will.
So the approach is to show it for one digit numbers, then two digit numbers, etc.
Consider 0<N<10. N3-N = N * (N2-1) = N * (N-1) * (N+1). One these must be a multiple of 3.
Now consider a number <100 which is 10M+N. Then we would like M3-10M to be a multiple of 3. This is the same as (M3-M)-9*M. The former (M3-M) is divisible by 3 (as per above) and 9*M is also divisible by 3. Hence the difference is divisible by 3. This proves the case for two digit numbers.
Similar logic will apply to any other digit in the number since it will split into (L3-L)-999....999*L.
Hence it applies to all integers.
Quote: unJonDid it quick in my head but looks like:
153
Quote: teliot153 -- which, coincidentally, is the smallest integer > 1 that is the sum of the cubes of its digits. 153 = 1^3 + 5^3 + 3^3. There are three more positive integers > 1 with this property. Bonus easy Monday question -- What are they?
Bonus bonus question -- how many fish did Simon Peter catch (New Testament)?
Quote: ThatDonGuy
By 891, one of 1, 8, 9 is in the code, but by 849, neither 8 nor 9 are in the code, so 1 is in the code, but not the third digit
By 317, 1 is not the second digit; therefore, 1 is the first digit
By 793, either 9 is the second digit or 3 is the third digit, but by 849, 9 is not in the code, so 3 is the third digit
By 725, either 7 or 5 is the second digit, but by 793, since 3 is in the code, 7 is not, so 5 is the second digit
The code is 153
Correct!
------------------------------

Quote: unJonDid it quick in my head but looks like:
153
P.S. This 89 second solve shatters the old speed record!
Quote: teliot...Hmmm .... not sure I like the "similar logic will apply" part. Can you formalize that?
Every integer (ABC....Z) can be considered A*10n+B*10(n-1)...Z. The sum of the integer cubes is A3+B3+...+Z3.
Consider the A part. The difference = A*10n-A3 = A*(10n-1)+A-A3. The first part, being 999....999 is divisible by 3. The second part, by previous proof, is divisible by 3.
Hence A*10n-A3 is divisible by 3.
Since this would apply to all the other digits in any number (B,C, .... Z); the condition is true for all integers.
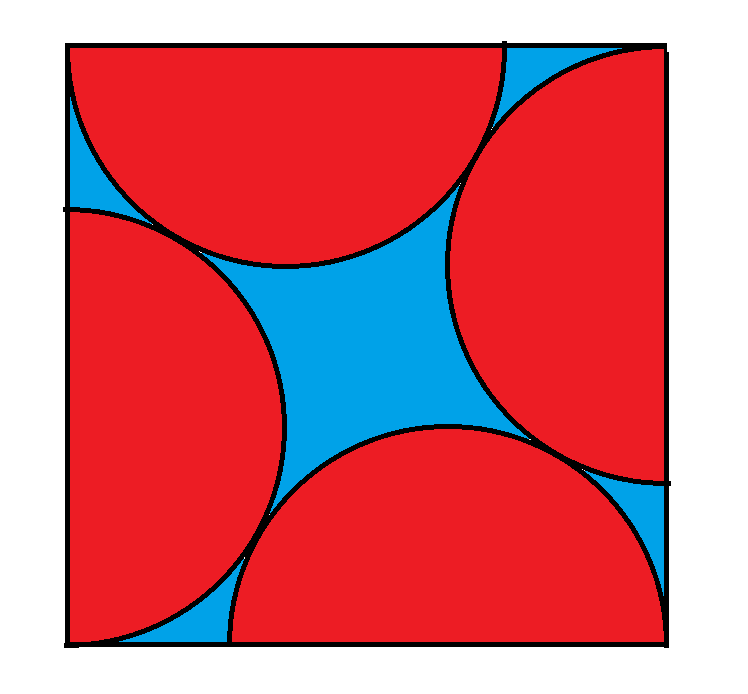
Four congruent semicircles are arranged in a square. The radius of each circle is 1, what is the length of a side of the square?
Quote: Wizard
Four congruent semicircles are arranged in a square. The radius of each circle is 1, what is the length of a side of the square?
Call the centers of the topmost and rightmost circles O and P, respectively. And let point A be the upper right corner of the square.
Line segment OP is the hypotenuse of triangle OAP. OP = 2 and AP = 1. Therefore, OA = (22-12)1/2 = 31/2.
Add 1 to the above length to get the side of the square: 31/2 + 1
Quote: ChesterDog
Call the centers of the topmost and rightmost circles O and P, respectively. And let point A be the upper right corner of the square.
Line segment OP is the hypotenuse of triangle OAP. OP = 2 and AP = 1. Therefore, OA = (22-12)1/2 = 31/2.
Add 1 to the above length to get the side of the square: 31/2 + 1
Winner, winner, chicken dinner!
Quote: charliepatrickEarlier the proof was given for (X-X3) would be a multiple of 3. Now to show it applies to all larger integers.
Every integer (ABC....Z) can be considered A*10n+B*10(n-1)...Z. The sum of the integer cubes is A3+B3+...+Z3.
Consider the A part. The difference = A*10n-A3 = A*(10n-1)+A-A3. The first part, being 999....999 is divisible by 3. The second part, by previous proof, is divisible by 3.
Hence A*10n-A3 is divisible by 3.
Since this would apply to all the other digits in any number (B,C, .... Z); the condition is true for all integers.
This appears to be an induction proof on the number of digits in the number. I'm still shaky on its logic, maybe just getting too old to make sense of things.
Here is my proof:

Quote: teliotOkay, which leads me to a cute little theorem-ette that is on the slightly non-trivial side (but not that non-trivial), related to the 153 question.
Let N > 0 be any integer. Let S be the sum of the cubes of its digits. Show that the difference (N-S) is always divisible by 3.
For example, N = 1263. S = 1^3 + 2^3 + 6^3 + 3^3 = 1 + 8 + 216 + 27 = 252. N - S = 1011= 3*337.
I have a feeling I am repeating at least one earlier answer...
Let {a0, a1, a2, ...} be a set of integers in {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} such that N = a0 + 10 a1 + 100 a2 + ... + 10k ak + ...
Since 10k - 1 = 9 (1 + 10 + 100 + ... + 10k-1), N = 3 (3 + 30 + ... +3 x 10k-1) + a0 + a1 + a2 + ..., this means that the difference between N and the sum of the cubes of its digits = a multiple of 3 + the sum of (each digit and the cube of that digit).
As has been pointed out earlier in the thread, for any digit K, K3 - K = K (K2 - 1) = (K-1) K (K+1);
since one of those must be a multiple of 3, K3 - K is always a multiple of 3, so the difference between N and the sum of the cubes of its digits is the sum of multiples of 3.
:strip_icc()/pic6014576.png)
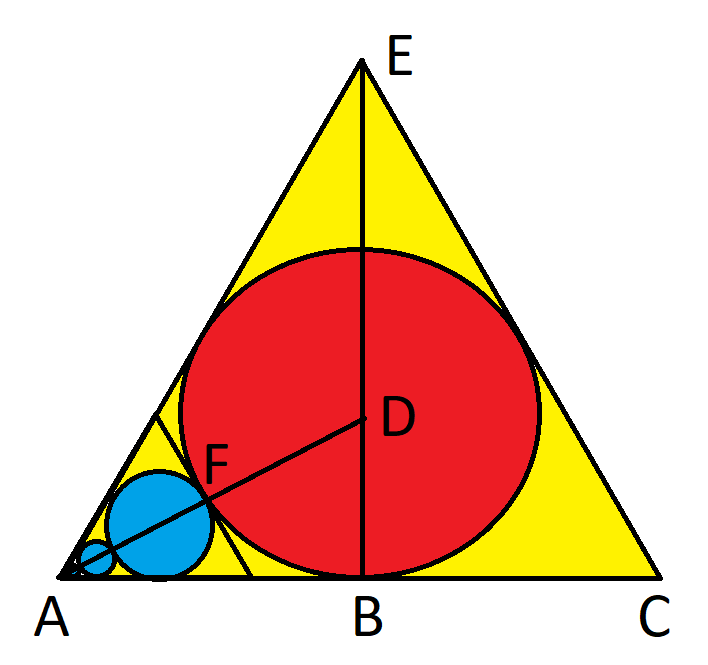
A circle is inscribed inside an equilateral triangle and an infinite set of circles are nested inside such that each circle touches the previous circle and the edges of the triangle act as tangents.
What fraction of the large red circle do the infinite set of smaller circles represent?
1) Let red circle have radius R, thus area (pi*R^2)
2) Name some points
A = top of triangle, C = center of red circle, D = center of bottom side of triangle. ACD is a line and bisects the 60 degree angle of the triangle.
B = intersection of ACD with red circle (nearest A)
D= center of left side of triangle.
3) ACD is right triangle and
CD/(AB+BC) = R/(AB+R) = sin30=.5
So AB=R
4)Height of triangle = AB+BC+CD=R+R+R=3R
5) So for a triangle of height 3R, we can fit a circle of size R
6) Draw horizontal tangent to red circle at B (top tip of the triangle). That forms a triangle with height AB=R, so the first inscribed circle must have radius R/3. Then the next triangular tip has height R/3, and inscribed circle has height R/9........
So the set of smaller circles on the top have area
pi*(R/3)^2 + pi*(R/9)^2+....geometric series = pi*(R/3)^2 / (1-1/9) = (pi*R^2)/8
So the three sets of circles have area (3/8) (pi*R^2) = 3/8 Area of red circle
Let ABC be the triangle, and O the center of the inscribed circle. Assume the radius of the big circle is 1.
Let D and E be the points on AB and BC tangent to the circle. ODB and OEB are congruent (hypotenuse-leg); since ABC = 60 degrees, ODB is a 30-60-90 triangle with OBD = 30 degrees.
Since OD = 1, this means OB = 2.
Let F be the point where the big circle is tangent to the largest of the smaller circles near B. OB = 2 and OF = 1, so FB = 1.
Draw the tangent to the two circles that touch at F, and let G and H be the points where this tangent intersects AB and BC.
BFG is a 30-60-90 triangle with BF = 1 and FBG = 30 degrees, so BG = 2 sqrt(3) / 3.
BGH and BHG are both 60 degrees, so triangles GBH and ABC are similar, with a length ratio of (2 sqrt(3) / 3) / 4 = sqrt(3) / 6.
The area ratio = the square of the length ratio = 1/12.
This process can be continued with each of the other small circles, so in terms of the area of the largest circle, the area of all of the small circles = 3 x (1/12 + (1/12)^2 + (1/12)^3 + ...)
= 3 x 1/12 x (1 + 1/12 + (1/12)^2 + ...)
= 1/4 x (1 / (1 - 1/12))
= 1/4 x 12/11 = 3/11
I see I agree with Chevy. If we're both right, please give him credit for being first.
Good problem.
Quote: ThatDonGuy
BFG is a 30-60-90 triangle with BF = 1 and FBG = 30 degrees, so BG = 2 sqrt(3) / 3.
BGH and BHG are both 60 degrees, so triangles GBH and ABC are similar, with a length ratio of (2 sqrt(3) / 3) / 4 = sqrt(3) / 6.
The area ratio = the square of the length ratio = 1/12.
If I am following your argument, it seems you are saying ABC has a side of 4?
You have FB=1 (I agree) and the diameter of the circle is 2. So doesn't ABC has HEIGHT of 3, then side of 2sqrt(3) from 30-60-90 triangle???
If so, then your length ratio is (2sqrt(3)/3) / (2sqrt(3)) = 1/3.
Area scales as 1/9.
If so, then it agrees with me and Wiz, if not, I am missing something in your construction.
A circle is inscribed in an equilateral triangle. What is the ratio of the area of the circle to the triangle?
Also, here is a diagram that may help in discussion.
Yes, sub question as part of the work done in last question.
ADB is 30-60-90 with DB = R.
As in previous problem
DB/AD=sin(30)=1/2
So AD = 2R = ED
And EB = ED+DB=2R + R = 3R
Also
DB/AB=tan30 = 1/sqrt(3)
So AB = sqrt(3)*R
Area of triangle = .5 * EB * AC = .5*EB *(2AB) = 3sqrt(3) R^2
So If you mean a single (red) circle)
Circle/Triangle = pi/(3sqrt(3))
If you meant area of all the circles (red +blue)
All circles area = piR^2 + (3/8) piR^2 =11/8 pi*R^2 ....from previous problem
circle/triangle = 11 pi / (24 sqrt(3))
Quote: chevy
If I am following your argument, it seems you are saying ABC has a side of 4?
You have FB=1 (I agree) and the diameter of the circle is 2. So doesn't ABC has HEIGHT of 3, then side of 2sqrt(3) from 30-60-90 triangle???
If so, then your length ratio is (2sqrt(3)/3) / (2sqrt(3)) = 1/3.
Area scales as 1/9.
If so, then it agrees with me and Wiz, if not, I am missing something in your construction.
No, you're right. I did have that distance as 4 by mistake.
Quote: chevy
1) Let red circle have radius R, thus area (pi*R^2)
2) Name some points
A = top of triangle, C = center of red circle, D = center of bottom side of triangle. ACD is a line and bisects the 60 degree angle of the triangle.
B = intersection of ACD with red circle (nearest A)
D= center of left side of triangle.
3) ACD is right triangle and
CD/(AB+BC) = R/(AB+R) = sin30=.5
So AB=R
4)Height of triangle = AB+BC+CD=R+R+R=3R
5) So for a triangle of height 3R, we can fit a circle of size R
6) Draw horizontal tangent to red circle at B (top tip of the triangle). That forms a triangle with height AB=R, so the first inscribed circle must have radius R/3. Then the next triangular tip has height R/3, and inscribed circle has height R/9........
So the set of smaller circles on the top have area
pi*(R/3)^2 + pi*(R/9)^2+....geometric series = pi*(R/3)^2 / (1-1/9) = (pi*R^2)/8
So the three sets of circles have area (3/8) (pi*R^2) = 3/8 Area of red circle
Quote: Wizard3/8.
I see I agree with Chevy. If we're both right, please give him credit for being first.
Good problem.
Correct!!
Well done.
:strip_icc()/pic6021770.png)
-------------------------------
I was going to tell this joke about infinity...
...but I don't know how it ends.
I have a follow-up question to my follow-up question. And I don't know the answer to this.Quote: teliotOk, here is a really easy follow-up question. The list in the spoiler gives all six solutions to "sum of the cubes of the digits equals the number."
My follow-up question is to find all integers that minimize the difference when it is greater than 0, that is:
minimize |(sum of cube of digits of number) - number| > 0
There are six solutions when this difference is equal to 0. I found 12 solutions to the next smallest difference.
We proved above that if N > 0 is an integer and S is the sum of the cubes of its digits, then the difference |N - S| is always divisible by 3. In my computer investigations, I've noticed that every multiple of 3 appears as the difference, at least as far up as I checked. I don't know if the following is true or false:
True or False? Let D >= 0 be divisible by 3. Then there is a positive integer N such that |N -S| = D.
Any takers?
Quote: teliotI have a follow-up question to my follow-up question. And I don't know the answer to this.
We proved above that if N > 0 is an integer and S is the sum of the cubes of its digits, then the difference |N - S| is always divisible by 3. In my computer investigations, I've noticed that every multiple of 3 appears as the difference, at least as far up as I checked. I don't know if the following is true or false:
True or False? Let D >= 0 be divisible by 3. Then there is a positive integer N such that |N -S| = D.
Any takers?
The simplest method is to consider that any six-digit numbers can have a maximum sum of cubes of 6*93=4374, so the difference must exceed 95626. For longer numbers the difference just keeps getting bigger.
Thus if you haven't found all the four digit numbers by then, you never will.
Brute force shows there are several values that haven't been found (assuming my coding is correct!)
Agree ... I just came up with the following list of counterexamples up to D=3000:Quote: charliepatrickFalse - try finding 651, 681, 909 etc.
The simplest method is to consider that any six-digit numbers can have a maximum sum of cubes of 6*93=4374, so the difference must exceed 95626. For longer numbers the difference just keeps getting bigger.
Thus if you haven't found all the four digit numbers by then, you never will.
Brute force shows there are several values that haven't been found (assuming my coding is correct!)
651
681
909
930
933
966
1398
1410
1422
1434
1437
1458
1461
1494
1515
1530
1578
1593
1644
1674
1743
1923
1926
1959
2202
2226
2391
2403
2415
2418
2439
2442
2475
2496
2511
2559
2574
2595
2625
2655
2724
2904
2907
2940
There's a new game that consists of a keno blower with 100 balls, each numbered 1 through 100. Ten balls are drawn at random, and you win $1 multiplied by the lowest of the ten numbers. For example, if the balls 2, 8, 14, 15, 27, 45, 54, 62, 89, and 99 were drawn, you would win $2, as 2 is the lowest number.
What is the expected return (i.e. the mean value) of the game?
Hang on, let me just iterate through the combin(100,10) (approximately 17,310,300,000,000) outcomes.Quote: ThatDonGuyHere's one:
There's a new game that consists of a keno blower with 100 balls, each numbered 1 through 100. Ten balls are drawn at random, and you win $1 multiplied by the lowest of the ten numbers. For example, if the balls 2, 8, 14, 15, 27, 45, 54, 62, 89, and 99 were drawn, you would win $2, as 2 is the lowest number.
What is the expected return (i.e. the mean value) of the game?
Quote: ThatDonGuyThere's a new game that consists of a keno blower with 100 balls, each numbered 1 through 100. Ten balls are drawn at random, and you win $1 multiplied by the lowest of the ten numbers. For example, if the balls 2, 8, 14, 15, 27, 45, 54, 62, 89, and 99 were drawn, you would win $2, as 2 is the lowest number.
What is the expected return (i.e. the mean value) of the game?
In case anyone is wondering, for the 80/20 case, as in keno, the answer is 3.857143
So, here is a slightly harder version --Quote: ThatDonGuyHere's one:
There's a new game that consists of a keno blower with 100 balls, each numbered 1 through 100. Ten balls are drawn at random, and you win $1 multiplied by the lowest of the ten numbers. For example, if the balls 2, 8, 14, 15, 27, 45, 54, 62, 89, and 99 were drawn, you would win $2, as 2 is the lowest number.
What is the expected return (i.e. the mean value) of the game?
A a keno blower has 100 balls, each numbered 1 through 100. Ten balls are drawn at random and recorded. After the ten balls are drawn, the lowest number recorded out of the 10 balls is then discarded and another ball is drawn from the blower to replace it. You then win $1 multiplied by the lowest of the ten numbers.
What is the expected win, to the nearest cent?
Here is a casino game version, with a strategic decision. After observing the first ten balls drawn, you are allowed to hit or stand. Hitting means that you discard the lowest and re-draw, with the lowest of that new group of 10 being your payout. Standing means you keep the original10 balls and make the lowest of those your payout. What is optimal strategy and what is the expected win in this game?
If you stand you win will X.
If you discard X then there are three possibilities for the next ball B
(i) is less than X, you will win that value and have lost X-B.
(ii) is between X and Y, you will win that value and have won B-X
(iii) is greater than Y, you win will Y and have won Y-X.
As an example 40 50 61 62 63 64 65 66 67 68. (i) 1-39 lose between 1 and 39 (ii) 41-49 gain 1 thru 9 (iii) 51+ gain 10 (note there are 50-8 of these regardless of Z's) So on average you lose 3.5 by drawing.
In theory this is a function of X and Y.
I'm guessing you could work out the chances of the lowest number being 1,2,3 etc. using permutations. I'm quite so sure how you do the second lowest.
Edit: Changed average as had typo in my quick spreadsheet. See my later answer which looks at this example again.
This is pretty much how I envisioned the closed solution being computed as well. But, it's definitely a lot of work and I would want to simulate my answer to verify. So I just ran some quick and dirty C code instead. :)Quote: charliepatrickLet the ten first numbers be, from lowest, X Y Z1 Z2...Z8. It transpires you don't care what the Z's actually are. You only need to know 8 numbers between Y and 100 have already been picked.
If you stand you win will X.
If you discard X then there are three possibilities for the next ball B
(i) is less than X, you will win that value and have lost X-B.
(ii) is between X and Y, you will win that value and have won B-X
(iii) is greater than Y, you win will Y and have won Y-X.
As an example 40 50 61 62 63 64 65 66 67 68. (i) 1-39 lose between 1 and 39 (ii) 41-49 gain 1 thru 9 (iii) 51+ gain 10 (note there are 50-8 of these regardless of Z's) So on average you lose 3.61111 by drawing.
In theory this is a function of X and Y.
I'm guessing you could work out the chances of the lowest number being 1,2,3 etc. using permutations. I'm quite so sure how you do the second lowest.
Quote: teliotHang on, let me just iterate through the combin(100,10) (approximately 17,310,300,000,000) outcomes.
No, really, there's an easy Excel solution. I get 101/11 = $9.18181818 ... as the expected payout. Charge $10 to play the game and you'll make a tidy profit.
Quote: Wizard9.181818182
In case anyone is wondering, for the 80/20 case, as in keno, the answer is 3.857143
Both answers are correct.
This involves something called the Hockey Stick Identity:
C(n,n) + C(n+1,1) + C(n+2,n) + ... + C(n+k,n) = C(n+k+1,n+1)
It gets its name from the fact that, if you iterate the values over Pascal's triangle, the path resembles a hockey stick.
Anyway, there are C(100,10) sets of numbers.
If the smallest number is N, the other numbers must be in the 100-N numbers > N, so there are C(100-N,9) sets of numbers where the smallest number is N.
The sum of the smallest numbers of all C(100,10) sets is:
1 x C(99,9) + 2 x C(98,9) + 3 x C(97,9) + ... + 90 x C(10,9) + 91 x C(9,9)
= (C(99,9) + C(98,9) + ... + C(9,9)) + (C(98,9) + C(97,9) + ... + C(9,9)) + (C(97,9) + C(96,9) + ... + C(9,9)) + ... + (C(10,9) + C(9,9)) + C(9,9)
Use the hockey stick identity on each group and the fact that C(9,9) = 1 = C(10,10) to get C(100,10) + C(99,10) + ... C(10,10)
Use the hockey stick identity to get C(101,11) for the sum
The expected value = C(101,11) / C(100,10)
= (101! / (11! 90!)) / (100! / (10! 90!)) = 101! / 11! x 10! / 100! = (101 x 100!) / (11 x 10!) x 10! / 100! = 101/11.
Quote: teliotThis is pretty much how I envisioned the closed solution being computed as well. But, it's definitely a lot of work and I would want to simulate my answer to verify. So I just ran some quick and dirty C code instead. :)
I: 1 J: 2 Perms: 157366449604 Profit: 1 Win: 2
I: 1 J: 3 Perms: 144520208820 Profit: 1.988888888888889 Win: 2.988888888888889
I: 1 J: 4 Perms: 132601016340 Profit: 2.966666666666667 Win: 3.966666666666667
I: 1 J: 5 Perms: 121550931645 Profit: 3.933333333333333 Win: 4.933333333333334
I: 1 J: 6 Perms: 111315063717 Profit: 4.888888888888889 Win: 5.888888888888889
I: 1 J: 7 Perms: 101841441273 Profit: 5.833333333333333 Win: 6.833333333333333
I: 1 J: 8 Perms: 93080887185 Profit: 6.766666666666667 Win: 7.766666666666667
I: 1 J: 9 Perms: 84986896995 Profit: 7.688888888888889 Win: 8.68888888888889
I: 1 J: 10 Perms: 77515521435 Profit: 8.6 Win: 9.6
I: 1 J: 11 Perms: 70625252863 Profit: 9.5 Win: 10.5
....
I: 88 J: 89 Perms: 165 Profit: -42.5 Win: 88
I: 88 J: 90 Perms: 45 Profit: -42.477777777777774 Win: 88
I: 88 J: 91 Perms: 9 Profit: -42.46666666666667 Win: 88
I: 88 J: 92 Perms: 1 Profit: -42.46666666666667 Win: 88
I: 89 J: 90 Perms: 45 Profit: -43.48888888888889 Win: 89
I: 89 J: 91 Perms: 9 Profit: -43.477777777777774 Win: 89
I: 89 J: 92 Perms: 1 Profit: -43.477777777777774 Win: 89
I: 90 J: 91 Perms: 9 Profit: -44.48888888888889 Win: 90
I: 90 J: 92 Perms: 1 Profit: -44.48888888888889 Win: 90
I: 91 J: 92 Perms: 1 Profit: -45.5 Win: 91
AvWin: 16.22254798150687
totalprofit=0;
totalperms=0;
for (i=1; i<=91; i++) {
for (j=i+1; j<=92; j++) {
perms=(100-j)*(99-j)*(98-j)*(97-j)*(96-j)*(95-j)*(94-j)*(93-j)/8/7/6/5/4/3/2;
profit=0;
if (i>1) { for (k=1; k<i; k++) {profit+=k-i;};};
if (j>i+1) { for (k=i+1; k<j; k++) {profit+=k-i;};};
if (j<92) { for (k=j+9; k<=100; k++) {profit+=j-i;};};
profit=profit/90;
outline=" ";
outline+="I: "+i+" ";
outline+="J: "+j+" ";
outline+="Perms: "+perms+" ";
outline+="Profit: "+profit+" ";
win=i; if (profit>0) {win=i+profit;};
outline+="Win: "+win+" ";
outline+="<BR>";
document.write(outline);
totalprofit+=win*perms;
totalperms+=perms;
}; };
average=totalprofit/totalperms;
outline+="AvWin: "+average+" ";
outline+="<BR>";
document.write(outline);
Quote: charliepatrickI haven't checked the answers yet, but this is what it produced.I: 1 J: 2 Perms: 157366449604 Profit: 1 Win: 2
I: 1 J: 3 Perms: 144520208820 Profit: 1.988888888888889 Win: 2.988888888888889
I: 1 J: 4 Perms: 132601016340 Profit: 2.966666666666667 Win: 3.966666666666667
I: 1 J: 5 Perms: 121550931645 Profit: 3.933333333333333 Win: 4.933333333333334
I: 1 J: 6 Perms: 111315063717 Profit: 4.888888888888889 Win: 5.888888888888889
I: 1 J: 7 Perms: 101841441273 Profit: 5.833333333333333 Win: 6.833333333333333
I: 1 J: 8 Perms: 93080887185 Profit: 6.766666666666667 Win: 7.766666666666667
I: 1 J: 9 Perms: 84986896995 Profit: 7.688888888888889 Win: 8.68888888888889
I: 1 J: 10 Perms: 77515521435 Profit: 8.6 Win: 9.6
I: 1 J: 11 Perms: 70625252863 Profit: 9.5 Win: 10.5
....
I: 88 J: 89 Perms: 165 Profit: -42.5 Win: 88
I: 88 J: 90 Perms: 45 Profit: -42.477777777777774 Win: 88
I: 88 J: 91 Perms: 9 Profit: -42.46666666666667 Win: 88
I: 88 J: 92 Perms: 1 Profit: -42.46666666666667 Win: 88
I: 89 J: 90 Perms: 45 Profit: -43.48888888888889 Win: 89
I: 89 J: 91 Perms: 9 Profit: -43.477777777777774 Win: 89
I: 89 J: 92 Perms: 1 Profit: -43.477777777777774 Win: 89
I: 90 J: 91 Perms: 9 Profit: -44.48888888888889 Win: 90
I: 90 J: 92 Perms: 1 Profit: -44.48888888888889 Win: 90
I: 91 J: 92 Perms: 1 Profit: -45.5 Win: 91
AvWin: 16.22254798150687totalprofit=0;
totalperms=0;
for (i=1; i<=91; i++) {
for (j=i+1; j<=92; j++) {
perms=(100-j)*(99-j)*(98-j)*(97-j)*(96-j)*(95-j)*(94-j)*(93-j)/8/7/6/5/4/3/2;
profit=0;
if (i>1) { for (k=1; k<i; k++) {profit+=k-i;};};
if (j>i+1) { for (k=i+1; k<j; k++) {profit+=k-i;};};
if (j<92) { for (k=j+9; k<=100; k++) {profit+=j-i;};};
profit=profit/90;
outline=" ";
outline+="I: "+i+" ";
outline+="J: "+j+" ";
outline+="Perms: "+perms+" ";
outline+="Profit: "+profit+" ";
win=i; if (profit>0) {win=i+profit;};
outline+="Win: "+win+" ";
outline+="<BR>";
document.write(outline);
totalprofit+=win*perms;
totalperms+=perms;
}; };
average=totalprofit/totalperms;
outline+="AvWin: "+average+" ";
outline+="<BR>";
document.write(outline);
Can you double check these lines?
if (i>1) { for (k=1; k<i; k++) {profit+=k-i;};};
if (j>i+1) { for (k=i+1; k<j; k++) {profit+=k-i;};};
if (j<92) { for (k=j+9; k<=100; k++) {profit+=j-i;};};
Thanks!
I've checked a few examples and they look good.Quote: teliot...double check these lines...
I: 2 J: 3 Perms: 144520208820 Profit: 0.9777777777777777 Win: 2.977777777777778
If the drawn ball is higher than 3 you win 3; only if the new ball drawn in 1 will you not receive 3. The chances of this are 1 in 90 and it loses you 2. So the average is 3 less 2/90. Check.
I: 40 J: 50 Perms: 536878650 Profit: -3.5 Win: 40 T1: -780 T: 39 T1: -735 T: 48 T1: -315 T: 90
From 1 thru 39 you lose 39 thru 1 = -780 (average of -1 and -39 = -20, number of items = 39, total = -780).
From 41 thru 49 you gain 1 thru 9 = +45 (average of 1 and 9 = 5, number of items = 9, total +45.
The remaining 51 to 100 except for the 8 balls already drawn each gain 10. There are 42 os these so total = +420.
420+45-780 = -315. -315/90 = -3.5. Check.
OK, I see where we differ and what my problem was.Quote: charliepatrickThere are 90 possible values for the redrawn ball (I'm assuming it can't be ones you've already got or the one you discarded).
I: 2 J: 3 Perms: 144520208820 Profit: 0.9777777777777777 Win: 2.977777777777778
If the drawn ball is higher than 3 you win 3; only if the new ball drawn in 1 will you not receive 3. The chances of this are 1 in 90 and it loses you 2. So the average is 3 less 2/90. Check.
I: 40 J: 50 Perms: 536878650 Profit: -3.5 Win: 40 T1: -780 T: 39 T1: -735 T: 48 T1: -315 T: 90
From 1 thru 39 you lose 39 thru 1 = -780 (average of -1 and -39 = -20, number of items = 39, total = -780).
From 41 thru 49 you gain 1 thru 9 = +45 (average of 1 and 9 = 5, number of items = 9, total +45.
The remaining 51 to 100 except for the 8 balls already drawn each gain 10. There are 42 os these so total = +420.
420+45-780 = -315. -315/90 = -3.5. Check.
You are only recording the profit if profit > 0. Essentially, you solved the second problem, optimal play, not the first. I re-wrote your code without the line "if profit > 0" in it and we came up with the same answer.
Oh, I see you added a NB above.
Very nice!!!
#include <stdio.h>
int main() {
int i, j, k;
double totalprofit = 0;
double totalperms = 0;
double profit, perms, win, num;
for (i=1; i<=91; i++) {
for (j=i+1; j<=92; j++) {
perms=(100.0-j)*(99-j)*(98-j)*(97-j)*(96-j)*(95-j)*(94-j)*(93-j)/(2.0*3*4*5*6*7*8);
profit=0;
num = 0;
if (i>1) {
for (k=1; k<i; k++) {
profit+=(k-i);
num++;
}
}
if (j>i+1) {
for (k=i+1; k<j; k++) {
profit+=(k-i);
num++;
}
}
if (j<92) {
for (k=j+9; k<=100; k++) {
profit+=(j-i);
num++;
}
}
profit = profit/num;
win = i+profit;
totalprofit += (win*perms);
totalperms += perms;
}
}
printf("%1.6f\n", totalprofit/totalperms);
return 0;
}
$ ./a.exe
16.068182
Optimal strategy -- thanks to charliepatrick for the code.
Minimum pair (i,j) with i < j to draw a second ball to replace i.
1, 2
2, 3
3, 4
4, 5
5, 6
6, 7
7, 8
8, 9
9, 10
10, 11
11, 12
12, 13
13, 15
14, 16
15, 17
16, 18
17, 19
18, 21
19, 22
20, 23
21, 25
22, 26
23, 27
24, 29
25, 30
26, 32
27, 33
28, 35
29, 36
30, 38
31, 40
32, 42
33, 43
34, 45
35, 47
36, 49
37, 52
38, 54
39, 56
40, 59
41, 62
42, 65
43, 69
44, 73
45, 79
Return = 16.222548
Quote: teliot
Optimal strategy -- thanks to charliepatrick for the code.
Got the same thing in Excel. The key to the problem was calculating the average draw value given the two lowest numbers, a and b:
(b*(b-1)/2-a+b*(100-b-8))/90
Quote: teliotSo, here is a slightly harder version --
A a keno blower has 100 balls, each numbered 1 through 100. Ten balls are drawn at random and recorded. After the ten balls are drawn, the lowest number recorded out of the 10 balls is then discarded and another ball is drawn from the blower to replace it. You then win $1 multiplied by the lowest of the ten numbers.
What is the expected win, to the nearest cent?
Suppose the lowest number in the 10 drawn is N.
Let K be the second-lowest number drawn.
The expected value of the lowest number after the draw is (probability that the 11th number < K) x (expected value of the 11th number) + (probability that the 11th number > K) x K.
Of the C(100 - N, 9) sets of 9 numbers > N, the lowest number (i.e. the second-lowest number in the original 10) is:
N + 1, with probability C(99 - N, 8) / C(100 - N, 9)
N + 2, with probability C(98 - N, 8) / C(100 - N, 9)
...
91, with probability C(9, 8) / C(100 - N, 9)
92, with probability C(8, 8) / C(100 - N, 9)
The expected value of the lowest number after the redraw is (K - 1) / 99 x (K + 1) / 2 + (100 - K) / 99 x K
= (K (200 - K) - 1) / 198
where K is the second-lowest number in the original 10
If the original lowest number is 10, the expected value is:
C(89, 8) / C(90, 9) x (11 x 189 - 1) / 198
+ C(88, 8) / C(90, 9) x (12 x 188 - 1) / 198
+ C(87, 8) / C(90, 9) x (13 x 187 - 1) / 198
+ ...
+ C(8, 8) / C(90, 9) x (92 x 8 - 1) / 198
This has to be calculated for each possible lowest number from 1 to 91, then multiply by the probability that it is the original lowest number, and sum the values.
Yes. If you look at some of the spoilers above, you will see an implementation of a slight simplification of this idea to solve the problem. Even more, the strategy problem has also been solved. Great work by charliepatrick.Quote: ThatDonGuy
Suppose the lowest number in the 10 drawn is N.
Let K be the second-lowest number drawn.
The expected value of the lowest number after the draw is (probability that the 11th number < K) x (expected value of the 11th number) + (probability that the 11th number > K) x K.
Of the C(100 - N, 9) sets of 9 numbers > N, the lowest number (i.e. the second-lowest number in the original 10) is:
N + 1, with probability C(99 - N, 8) / C(100 - N, 9)
N + 2, with probability C(98 - N, 8) / C(100 - N, 9)
...
91, with probability C(9, 8) / C(100 - N, 9)
92, with probability C(8, 8) / C(100 - N, 9)
The expected value of the lowest number after the redraw is (K - 1) / 99 x (K + 1) / 2 + (100 - K) / 99 x K
= (K (200 - K) - 1) / 198
where K is the second-lowest number in the original 10
If the original lowest number is 10, the expected value is:
C(89, 8) / C(90, 9) x (11 x 189 - 1) / 198
+ C(88, 8) / C(90, 9) x (12 x 188 - 1) / 198
+ C(87, 8) / C(90, 9) x (13 x 187 - 1) / 198
+ ...
+ C(8, 8) / C(90, 9) x (92 x 8 - 1) / 198
This has to be calculated for each possible lowest number from 1 to 91, then multiply by the probability that it is the original lowest number, and sum the values.
First, some explanation of my notation:
C(A,B) is the number of combinations of A things taken B at a time
SUM[B=2..92] {...} is the sum of the value within { } for all B from 2 to 92 inclusive; imagine a capital sigma with "B=2" at the bottom and "92" at the top.
Let A and B be the smallest and second-smallest numbers drawn; note that 1 <= A < B <= 92
There are C(100-B, 8) combinations of the C(100, 10) where this is true
If the 11th number < B, it is the lowest number after A is removed; there are B-2 numbers < B excluding A,
so the expected value of the lowest number in this case is (1 + 2 + ... + (B-1) - A) / (B-2) = ((B-1) B - 2A) / (2 (B-2)).
If the 11th number < B, then B is the lowest number after A is removed.
P(11th number < B) = (B - 2) / 90
P(11th number > B) = (92 - B) / 90
The expected value of the lowest number is
1 / C(100, 10) x SUM[B=2..92] {SUM[A=1..B-1] {C(100-B, 8) x (((B - 2) / 90)((B - 1) B - 2A) / (2 (B - 2)) + B (92 - B) / 90)}}
= 1 / C(100, 10) x SUM[B=2..92] {C(100-B, 8) x SUM[A=1..B-1] {((B - 1) B - 2A) / 180 + 2B (92 - B) / 180}}
= 1 / C(100, 10) x SUM[B=2..92] {C(100-B, 8) x SUM[A=1..B-1] {(183 B - B^2 - 2A) / 180}}
= 1 / (180 C(100, 10)) x SUM[B=2..92] {C(100-B, 8) x (SUM[A=1..B-1] {183 B - B^2} - SUM[A=1..B-1] {2A})}
= 1 / (180 C(100, 10)) x SUM[B=2..92] {C(100-B, 8) x ((B - 1)(183 B - B^2) - 2 (B - 1) B / 2)}
= SUM[B=2..92] {(183 B^2 - B^3 - 182 B) C(100-B, 8)} / (180 C(100, 10))
Okay, I needed a computer to calculate the sum, but it turns out to be 707 / 44.
What I love most about this is that you reduced the fraction ... the rest of us just got the decimal expansion. :) Nice!Quote: ThatDonGuyHere is a math solution (well, sort of) to the "slightly harder" problem with the 100 balls:
First, some explanation of my notation:
C(A,B) is the number of combinations of A things taken B at a time
SUM[B=2..92] {...} is the sum of the value within { } for all B from 2 to 92 inclusive; imagine a capital sigma with "B=2" at the bottom and "92" at the top.
Let A and B be the smallest and second-smallest numbers drawn; note that 1 <= A < B <= 92
There are C(100-B, 8) combinations of the C(100, 10) where this is true
If the 11th number < B, it is the lowest number after A is removed; there are B-2 numbers < B excluding A,
so the expected value of the lowest number in this case is (1 + 2 + ... + (B-1) - A) / (B-2) = ((B-1) B - 2A) / (2 (B-2)).
If the 11th number < B, then B is the lowest number after A is removed.
P(11th number < B) = (B - 2) / 90
P(11th number > B) = (92 - B) / 90
The expected value of the lowest number is
1 / C(100, 10) x SUM[B=2..92] {SUM[A=1..B-1] {C(100-B, 8) x (((B - 2) / 90)((B - 1) B - 2A) / (2 (B - 2)) + B (92 - B) / 90)}}
= 1 / C(100, 10) x SUM[B=2..92] {C(100-B, 8) x SUM[A=1..B-1] {((B - 1) B - 2A) / 180 + 2B (92 - B) / 180}}
= 1 / C(100, 10) x SUM[B=2..92] {C(100-B, 8) x SUM[A=1..B-1] {(183 B - B^2 - 2A) / 180}}
= 1 / (180 C(100, 10)) x SUM[B=2..92] {C(100-B, 8) x (SUM[A=1..B-1] {183 B - B^2} - SUM[A=1..B-1] {2A})}
= 1 / (180 C(100, 10)) x SUM[B=2..92] {C(100-B, 8) x ((B - 1)(183 B - B^2) - 2 (B - 1) B / 2)}
= SUM[B=2..92] {(183 B^2 - B^3 - 182 B) C(100-B, 8)} / (180 C(100, 10))
Okay, I needed a computer to calculate the sum, but it turns out to be 707 / 44.
Quote: teliot
Optimal strategy -- thanks to charliepatrick for the code.
Minimum pair (i,j) with i < j to draw a second ball to replace i.
1, 2
2, 3
3, 4
4, 5
5, 6
6, 7
7, 8
8, 9
9, 10
10, 11
11, 12
12, 13
13, 15
14, 16
15, 17
16, 18
17, 19
18, 21
19, 22
20, 23
21, 25
22, 26
23, 27
24, 29
25, 30
26, 32
27, 33
28, 35
29, 36
30, 38
31, 40
32, 42
33, 43
34, 45
35, 47
36, 49
37, 52
38, 54
39, 56
40, 59
41, 62
42, 65
43, 69
44, 73
45, 79
Return = 16.222548
I get 45,293,117,053,521 / 2,791,985,396,200, which is 16.222547981507
The strategy is to draw when A < (183 B - B^2) / 182, where A and B are the smallest and second-smallest numbers.
This is equivalent to B > 183/2 - sqrt(183^2 / 4 - 182 A) for B < 183/2.
It appears to match the above list of pairs.
Fabulous! It is surprising to me that using perfect strategy adds so little value.Quote: ThatDonGuyQuote: teliot
Optimal strategy -- thanks to charliepatrick for the code.
Minimum pair (i,j) with i < j to draw a second ball to replace i.
1, 2
2, 3
3, 4
4, 5
5, 6
6, 7
7, 8
8, 9
9, 10
10, 11
11, 12
12, 13
13, 15
14, 16
15, 17
16, 18
17, 19
18, 21
19, 22
20, 23
21, 25
22, 26
23, 27
24, 29
25, 30
26, 32
27, 33
28, 35
29, 36
30, 38
31, 40
32, 42
33, 43
34, 45
35, 47
36, 49
37, 52
38, 54
39, 56
40, 59
41, 62
42, 65
43, 69
44, 73
45, 79
Return = 16.222548
I get 45,293,117,053,521 / 2,791,985,396,200, which is 16.222547981507
The strategy is to draw when A < (183 B - B^2) / 182, where A and B are the smallest and second-smallest numbers.
This is equivalent to B > 183/2 - sqrt(183^2 / 4 - 182 A) for B < 183/2.
It appears to match the above list of pairs.
Here is another math problem.
Last night on the phone my grandson who just turned six asked me the question what is the number that comes just before a googolplex. I am interested to see what responses we get here.
ABC is an isosceles triangle, with sides AB and AC the same length.
A line going through one of the three points and intersecting the opposite side of the triangle divides the triangle into two non-congruent isosceles triangles.
For what values of angle BAC is this possible?
Quote: ThatDonGuyHere's another problem - this is one I was given when I was a freshman in high school (1977), although the original problem said there was only one solution, and I surprised the author when I came up with multiple solutions.
ABC is an isosceles triangle, with sides AB and AC the same length.
A line going through one of the three points and intersecting the opposite side of the triangle divides the triangle into two non-congruent isosceles triangles.
For what values of angle BAC is this possible?
First consider a line from B intersecting AC at a point D such that BC=BD and BD=AD. From {BAC} being isosceles if <BAC=x then <DCB=(180-x)/2. From {DBC} being isosceles this means <CDB=<DCB so <DBC=x. Since {BDA} is isosceles <ABD=x. So <CBA=2x=<DCB=(180-x)/2. So x=36 degrees. Note that BDC and ABC are similar.
Another solution is a relatively flatter triangle using a line from A to D. Using similar logic the angles are 36 36 108 for ABC and ADC, with ABD being 36 72 72.
Interestingly having created a triangle from the original ABC, you can now recreate the effect in both the new triangles .ADB and BDC.
Quote: teliot...Here is another math problem.
Last night on the phone my grandson who just turned six asked me the question what is the number that comes just before a googolplex. I am interested to see what responses we get here.
In the mathematical sense it depends on whether you're looking at just integers, in which case if you ordered them by value, N-1 comes just before N. I'm not sure how you order Real numbers since if you said N-x came just before N, then where does N-(x/2) come. I suppose given you've asked the question assuming there is an order to numbers, then you would mean the former; so it would be (googol-1).
References
https://www.wsj.com/articles/SB108575924921724042
Quote: https://en.wikipedia.org/wiki/GoogolplexIn 1920, Edward Kasner's nine-year-old nephew, Milton Sirotta, coined the term googol, which is 10100, and then proposed the further term googolplex to be "one, followed by writing zeroes until you get tired".[1] Kasner decided to adopt a more formal definition because "different people get tired at different times and it would never do to have Carnera a better mathematician than Dr. Einstein, simply because he had more endurance and could write for longer".[2] It thus became standardized to 10(10100).
I can only get one???
Let a line through B hit AC at point D
x=angle BAC=BAC (for short)
y=ABC=BCA
So for triangle ABC
x+2y=180
BDC=BCA=y Since smaller triangle BCD is isosceles
So BDA=180-y
DAB=DBA=x Since smaller triangle BAD is isosceles
So for triangle BAD
2x+(180-y)=180
y=2x
Back to triangle ABC
x+2y=180
x+2(2x)=180
x=36. (angle BAC)
Since line through B or line through C is same....this is only one I get.
For line through A, I would get BAC = 90, but that would divide the triangle into two identical (i.e congruent) smaller triangles.
So I am missing the other option you found.
EDIT: I see charliepatrick found other answer
Quote: charliepatrick36 or 108 degrees.
First consider a line from B intersecting AC at a point D such that BC=BD and BD=AD. From {BAC} being isosceles if <BAC=x then <DCB=(180-x)/2. From {DBC} being isosceles this means <CDB=<DCB so <DBC=x. Since {BDA} is isosceles <ABD=x. So <CBA=2x=<DCB=(180-x)/2. So x=36 degrees. Note that BDC and ABC are similar.
Another solution is a relatively flatter triangle using a line from A to D. Using similar logic the angles are 36 36 108 for ABC and ADC, with ABD being 36 72 72.
Interestingly having created a triangle from the original ABC, you can now recreate the effect in both the new triangles .ADB and BDC.
Keep going; you're getting there...
Quote: teliotLast night on the phone my grandson who just turned six asked me the question what is the number that comes just before a googolplex. I am interested to see what responses we get here.
I've answered this one before...
It's also nine times the googol'th repunit. The nth repunit is the n-digit positive integer all of whose digits are 1s. (The second repunit is 11, the third is 111, and so on.)
Quote: ThatDonGuyKeep going; you're getting there...
Rather than start with the triangle to be cut into half, I started with a resultant isosceles triangle and worked backwards trying to extend one of its sides to create another isosceles triangle. I looked at the ratio of angles and started with the base angles at 2x and top angle nx; using n=3 led to another answer that was <BAC=180/7.
Quote: charliepatrickQuote: ThatDonGuyHere's another problem - this is one I was given when I was a freshman in high school (1977), although the original problem said there was only one solution, and I surprised the author when I came up with multiple solutions.
ABC is an isosceles triangle, with sides AB and AC the same length.
A line going through one of the three points and intersecting the opposite side of the triangle divides the triangle into two non-congruent isosceles triangles.
For what values of angle BAC is this possible?36 or 108 degrees.
First consider a line from B intersecting AC at a point D such that BC=BD and BD=AD. From {BAC} being isosceles if <BAC=x then <DCB=(180-x)/2. From {DBC} being isosceles this means <CDB=<DCB so <DBC=x. Since {BDA} is isosceles <ABD=x. So <CBA=2x=<DCB=(180-x)/2. So x=36 degrees. Note that BDC and ABC are similar.
Another solution is a relatively flatter triangle using a line from A to D. Using similar logic the angles are 36 36 108 for ABC and ADC, with ABD being 36 72 72.
Interestingly having created a triangle from the original ABC, you can now recreate the effect in both the new triangles .ADB and BDC.Obviously you can cut a right angle triangle in half, but then the two triangles formed are congruent, assumed this wasn't a solution.
Rather than start with the triangle to be cut into half, I started with a resultant isosceles triangle and worked backwards trying to extend one of its sides to create another isosceles triangle. I looked at the ratio of angles and started with the base angles at 2x and top angle nx; using n=3 led to another answer that was <BAC=180/7.
That's all of them
Let ABC be an isosceles triangle with AB = AC
Let t be the measure of ABC (as well as ACB)
Case 1: D is on BC, forming triangles ABD and ACD
(a) If ABD = ADB, then ADB = t -> ADC = 180 - t -> CAD = 180 - (t + (180 - t)) = 0
(b) If ABD = BAD, then ADB = 180 - 2t -> ADC = 2t -> CAD = 180 - 3t
(b1) ADC = ACD -> 2t = t -> t = 0
(b2) ADC = CAD -> 2t = 180 - 3t -> t = 36 -> BAC = 108
108 is a solution: {108, 36, 36} -> {36, 36, 108} {72, 72, 36}
(b3) ACD = CAD -> t = 180 - 3t -> t = 45 -> ADB = ADC = 90 and BAD = CAD = 45 -> BAD and CAD are ASA-congruent
(c) If ADB = BAD, then ADB = 90 - t/2 -> ADC = 180 - (90 - t/2) = 90 + t/2 -> CAD = 180 - t - (90 + t/2) = 90 - 3/2 t
(c1) ADC = ACD -> 90 + t/2 = t -> t = 180
(c2) ADC = CAD -> 90 + t/2 = 90 - 3/2 t -> t = 0
(c3) ACD = CAD -> t = 90 - 3/2 t -> t = 36; this is the same as (b2)
Case 2: D is on AC, forming triangles ABD and CBD
Let p be the measure of ABD; CBD = t - p
Since BAC = 180 - 2t, ADB = 180 - p - (180 - 2t) = 2t - p
Since BCA = t, BDC = 180 - t - (t - p) = 180 - 2t + p
(a) If CBD = BCD, then t = t - p -> p = 0
(b) If CBD = CDB, then t - p = 180 + p - 2t -> p = 3/2 t - 90
BDA = 2t - (3/2 t - 90) = t/2 + 90; ABD = 3/2 t - 90
(b1) If BAD = ABD, then 180 - 2t = 3/2 t - 90 -> t = 540/7 -> p = 180/7
180/7 is a solution: {180/7, 540/7, 540/7} -> {180/7, 180/7, 900/7}, {360/7, 360/7, 540/7}
(b2) If BAD = BDA, then 180 - 2t = t/2 + 90 -> 90 = 5/2 t -> t = 36 -> p < 0
(b3) If ABD = BDA, then 3/2 t - 90 = t/2 + 90 -> t = 180
(c) If BCD = CDB, then t = 180 + p - 2t -> p = 3t - 180
BDA = 2t - (3t - 180) = 180 - t; ABD = 3t - 180
(c1) If BAD = ABD, then 180 - 2t = 3t - 180 -> t = 72 -> p = 36
36 is a solution: {36, 72, 72} -> {36, 108, 36} {36, 72, 72}
(c2) If BAD = BDA, then 180 - 2t = 180 - t -> t = 0
(c3) If ABD = BDA, then 3t - 180 = 180 - t -> t = 90 -> BAC = 180 - 2t = 0
Here is a nice algebra problem to chew on.
Solve the following system of equations for a, b, c, d, e, and f in real numbers other than the trivial solution of a = b = c = d = e = f = 0.
a + b + c + d + e = f^2
a + b + c + d + f = e^2
a + b + c + e + f = d^2
a + b + d + e + f = c^2
a + c + d + e + f = b^2
b + c + d + e + f = a^2


