Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
I think youíre saying you are familiar with normal distributions but not geometric ones. The former is for calculating variance from average given a set number of trials, the latter is for calculating the variance from average of the number trials required for an event to happen. The geometric distribution applies to this problem.Quote: davethebuilderQuote: Ace2Good approach and thatís a decent estimate, but thatís the standard deviation of exactly 14.7 rolls.Quote: davethebuilderQuote: Ace2Most of us know that the average number of rolls to hit all six numbers of a standard die at least once is 14.7
What's the standard deviation?
link to original postMean total of a single die roll is 3.5
Mean square of a single roll is (1+4+9+16+25) = 91/6
Variance: 91/6 - (3.5)² = 35/12
Sample size is 14.7 rolls
Variance: 35/12*14.7 = 42.875
Standard Deviation is the square root of the Variance
Standard Deviation = 6.548
link to original post
It takes an *average* of 14.7 rolls to hit all six numbers, not *exactly* 14.7 rolls. The number of rolls can be anywhere between six and infinity
After 15 rolls, there is an ~36% chance you have not hit all six numbers
link to original post
Noted, however, I'm not sure how to calculate an answer without using defined limits, that is, real numbers, so I'll wait for an answer.
link to original post
Not sure what you mean by ďreal numbersĒ. Itís like saying you canít calculate the variance of 100 coin flips without knowing first how many were heads
Quote: charliepatrickI suspect you chop every pill in half, eat half and leave half. That way you can take one half of the total pills today and leave the remainder for the other day.
link to original post
That is correct.
Quote: Ace2Most of us know that the average number of rolls to hit all six numbers of a standard die at least once is 14.7
What's the standard deviation?
link to original post
sqrt((72/25 - (6/5)^2) + (9/2 - (3/2)^2) + (8-2^2) + (18-3^2) + (72-6^2) ) =~ 7.26
I will show my method if this is at least correct to three significant digits.
Quote: Ace2Most of us know that the average number of rolls to hit all six numbers of a standard die at least once is 14.7
What's the standard deviation?
link to original post
I found the mistake in my earlier attempt - I had switched p and 1-p in one of the calculations.
I don't think this is a "Markov chain"; the mean and variance are the sums of the six independent events of rolling a unique number after having already rolled {0, 1, 2, 3, 4, 5} of them.
First, note that 1 + 4 p + 9 p^2 + 16 p^3 + ... = (p + 1) / (1 - p)^3
Let p(n) be the probability of rolling a unique number after n of them have been rolled: p(n) = (6-n) / 6
Let m(n) be the mean number of rolls needed to roll the nth unique number after n-1 have been rolled: m(n) = 1 / p
Let q(n) = 1 - p(n)
V(n) = (1 - q) ((1-m)^2 + q (2-m)^2 + q^2 (3-m)^2 + ...)
= (1 - q) ((1 + 4 q + 9 q^2 + 16 q^3 + ...) - 2m (1 + 2 q + 3 q^2 + 4 q^3 + ...) + m^2 (1 + q + q^2 + q^3 + ...))
= (1 - q) ((q + 1) / (1 - q)^3 - 2m / (1 - q)^2 + m^2 / (1 - q))
= (q + 1) / (1 - q)^2 - 2m / (1 - q) + m^2
= (2 - p) / p^2 - 2m / p + m^2
= (2 - p) / p^2 - 2 / p^2 + 1 / p^2
= (2 - p) / p^2 - 2 / p^2 + 1 / p^2
= (1 - p) / p^2
For n = 1, p = 5/6, and V = (1/6) / (25/36) = 6/25
For n = 2, p = 2/3, and V = (1/3) / (4/9) = 3/4
For n = 3, p = 1/2, and V = (1/2) / (1/4) = 2
For n = 4, p = 1/3, and V = (2/3) / (1/9) = 6
For n = 5, p = 1/6, and V = (5/6) / (1/36) = 30
SD = sqrt(the sum of the variances) = sqrt(3899) / 10, or about 6.2242
A customer has a requested a black Russian. You need to measure one ounce of vodka and 1/2 ounce of Kahlua to pour over ice in a glass. If you approximate the measurement of 1/2 ounce Kahlua (or 1 ounce vodka, which is dumb since you have a jigger with 1 ounce measurement), you are fired.
How do you prepare this drink with your equipment?
I agree with that answer (sqrt(3899) / 10) though you might have transposed digits in your decimal answer. There is a much easier approach which I'll post in a minute. Good job TDG 🍺Quote: ThatDonGuyQuote: Ace2Most of us know that the average number of rolls to hit all six numbers of a standard die at least once is 14.7
What's the standard deviation?
link to original post
I found the mistake in my earlier attempt - I had switched p and 1-p in one of the calculations.
I don't think this is a "Markov chain"; the mean and variance are the sums of the six independent events of rolling a unique number after having already rolled {0, 1, 2, 3, 4, 5} of them.
First, note that 1 + 4 p + 9 p^2 + 16 p^3 + ... = (p + 1) / (1 - p)^3
Let p(n) be the probability of rolling a unique number after n of them have been rolled: p(n) = (6-n) / 6
Let m(n) be the mean number of rolls needed to roll the nth unique number after n-1 have been rolled: m(n) = 1 / p
Let q(n) = 1 - p(n)
V(n) = (1 - q) ((1-m)^2 + q (2-m)^2 + q^2 (3-m)^2 + ...)
= (1 - q) ((1 + 4 q + 9 q^2 + 16 q^3 + ...) - 2m (1 + 2 q + 3 q^2 + 4 q^3 + ...) + m^2 (1 + q + q^2 + q^3 + ...))
= (1 - q) ((q + 1) / (1 - q)^3 - 2m / (1 - q)^2 + m^2 / (1 - q))
= (q + 1) / (1 - q)^2 - 2m / (1 - q) + m^2
= (2 - p) / p^2 - 2m / p + m^2
= (2 - p) / p^2 - 2 / p^2 + 1 / p^2
= (2 - p) / p^2 - 2 / p^2 + 1 / p^2
= (1 - p) / p^2
For n = 1, p = 5/6, and V = (1/6) / (25/36) = 6/25
For n = 2, p = 2/3, and V = (1/3) / (4/9) = 3/4
For n = 3, p = 1/2, and V = (1/2) / (1/4) = 2
For n = 4, p = 1/3, and V = (2/3) / (1/9) = 6
For n = 5, p = 1/6, and V = (5/6) / (1/36) = 30
SD = sqrt(the sum of the variances) = sqrt(3899) / 10, or about 6.2242
link to original post
Three concepts to solving this:Quote: Ace2Most of us know that the average number of rolls to hit all six numbers of a standard die at least once is 14.7
What's the standard deviation?
link to original post
1) The time it takes to roll any number is an independent event. For instance, the time needed to roll the third number has no effect on the time needed to roll the fourth number
2) The variances can be calculated separately for each number then summed to get the total variance for all six numbers
3) For a discrete random event with probability p, the expected waiting time for p to occur is 1/p with variance (1/p)^2 - 1/p
Therefore the variance of, for instance, rolling the second number is (6/5)^2 - 6/5 = 0.24. Applying this to all numbers gives us a total variance of:
(6/6)^2 + (6/5)^2 + (6/4)^2 + (6/3)^2 + (6/2)^2 + (6/1)^2 - 14.7 = 38.99
The final answer (SD) being (38.99)^.5
The variance of (1/p)^2 - 1/p can be expressed as (1/p)(1/p - 1), so the variance can also be calculated as:
1.2*0.2 + 1.5*0.5 + 2 + 3*2 + 6*5 = 38.99
The answer can be easily obtained via Markov chain with only six states. I'm quite surprised TDG and Wizard didn't do this first to at least verify the answer
The variance can also be obtained by integrating the following from zero to infinity:
(1 - 1/e^(x/6))^5 * 1/e^(x/6) * (x - 14.7)^2 dx
Note, the variance of a continuous random variable is (1/p)^2 vs (1/p)^2 - 1/p for the discrete variable so it must be reduced by the expected value of 14.7 to get to 38.99. I believe the difference exists because the sixth number can be rolled at any time >0 for the continuous variable but only for whole values >5 for the discrete variable
Quote: KevinAAYou work at a bar with limited equipment. The bottles do not have speed pourers (to measure volume dispensed by time). You have one jigger. The jigger has one ounce on one side and 1.5 ounces on the other side. You have one empty glass.
A customer has a requested a black Russian. You need to measure one ounce of vodka and 1/2 ounce of Kahlua to pour over ice in a glass. If you approximate the measurement of 1/2 ounce Kahlua (or 1 ounce vodka, which is dumb since you have a jigger with 1 ounce measurement), you are fired.
How do you prepare this drink with your equipment?
link to original post
Am I missing something?
Dog Hand
Quote: KevinAAYou work at a bar with limited equipment. The bottles do not have speed pourers (to measure volume dispensed by time). You have one jigger. The jigger has one ounce on one side and 1.5 ounces on the other side. You have one empty glass.
A customer has a requested a black Russian. You need to measure one ounce of vodka and 1/2 ounce of Kahlua to pour over ice in a glass. If you approximate the measurement of 1/2 ounce Kahlua (or 1 ounce vodka, which is dumb since you have a jigger with 1 ounce measurement), you are fired.
How do you prepare this drink with your equipment?
link to original post
Assuming you can't mix the vodka and Kahlua together in the jigger:
Pour 1.5 ounces of Kahlua into the jigger
Empty the jigger into the glass
Pour 1 ounce of the Kahlua in the glass into the jigger; this leaves 1/2 ounce of Kahlua in the glass
Dispose of the Kahlua in the jigger (e.g. drink it)
Pour the 1/2 ounce of Kahlua in the glass into the jigger
Put ice in the glass, then pour the Kahlua in the jigger into the glass, over the ice
Pour 1 ounce of vodka into the jigger, then pour that into the glass
Quote: DogHandAm I missing something?
Pour one ounce of vodka into the one ounce side of the jigger, pour the vodka into the glass, flip the jigger over to the 1.5 ounce side, pour the vodka into it, then add Kailua to the 1.5 ounce mark.
Dog Hand
correct
Quote: ThatDonGuyAssuming you can't just mix the vodka and Kahlua together in the jigger (i.e. pour 1 ounce Vodka into it, then pour Kahlua into it until it reaches 1.5 ounces)
Pour 1.5 ounces of Kahlua into the jigger
Empty the jigger into the glass
Pour 1 ounce of the Kahlua in the glass into the jigger; this leaves 1/2 ounce of Kahlua in the glass
Dispose of the Kahlua in the jigger (e.g. drink it)
Pour the 1/2 ounce of Kahlua in the glass into the jigger
Put ice in the glass, then pour the Kahlua in the jigger into the glass, over the ice
Pour 1 ounce of vodka into the jigger, then pour that into the glass
I didn't say you can't mix Kahlua and vodka together in the jigger. Why not? They get mixed together in the drink.
If you are not allowed to approximate 1/2 ounce (I say this because you can get 1/2 ounce measurement with reasonable accuracy in a 1 ounce jigger if you do some geometry assuming the jigger is a cone), you would certainly not be allowed to drink or throw away precisely 1 ounce Kahlua. That's a "you're fired" solution.
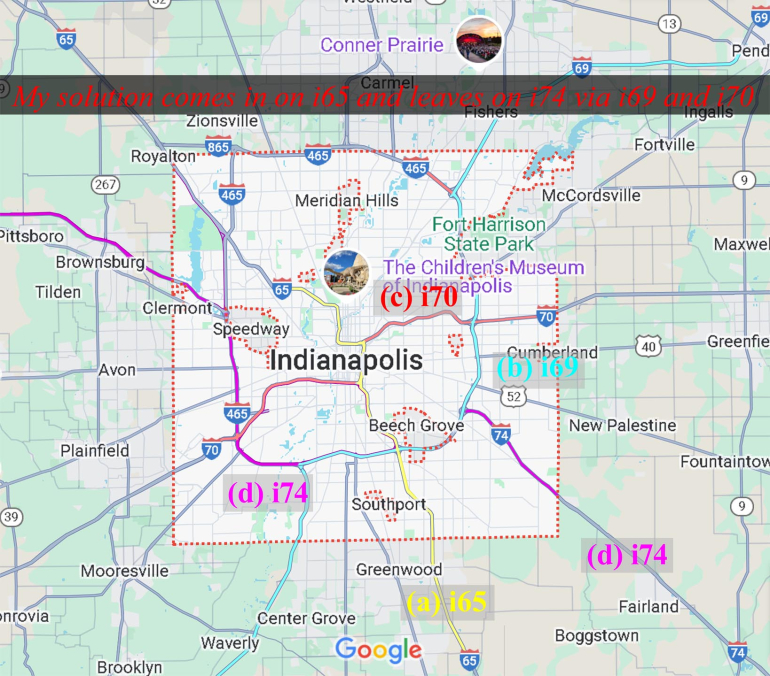
The objective is to travel only on one or two digit Interstate routes, making ones way from one side of the US to the other. Thus you start on I-5 and end up on I-95. Also when you change from one interstate to another you can only move onto a higher numbered one; the "cost" of making this move is the square of the difference. The objective is to find the "minimal cost" route.
As an example, obviously not the best route, you could go 5 - 10 - 15 - 90 - 95 the cost would be 25+25+5625+25 = 5700. A route such as 5 - 8 -10 - 55 - 90 - 95 would be better (9+4+2025+1225+25=3288).
btw I've only just heard about the problem so don't know the answer and here it's Bank Holiday weekend, so will look at it later! Personally I'll be assuming the wiki entries for interstates is correct.
https://en.wikipedia.org/wiki/Interstate_55 (you can enter the various numbers)
https://gisgeography.com/wp-content/uploads/2020/07/US-Road-Map.pdf (I don't know how accurate this is, but it is useful to see the direction of roads and which ones will never get near somewhere interesting, such as 19, 27 etc.)
https://www.visualcapitalist.com/wp-content/uploads/2017/10/us-interstates-as-a-subway-map.jpg
(i) The I35W and I35E can each be considered as part of I35 as it splits near Dallas.
(ii) Various Interstates near Indianapolis are continuous and either go through the city centre or, failing that, use the Ring Road (as google suggests) to connect them two parts. At times some if these routes could be using the same stretch of road, you can pick which route number you are using at that time.
Quote: charliepatrick^ Further to above I've had to make various assumptions about how Interstates meet each other in various cities and whether they can count. If someone knows definitely then please feel free to correct me, however I've assumed where an Interstate is on both sides of a major city, then somehow it has a continuous route across the city..
There's another discrepancy between "from one side of the country to the other" and "from I-5 to I-95." I-80 goes way to the west of I-5 and I-40 goes way to the east of I-95. So those are two different goals and there will be very different results.
Quote: charliepatrickThis is not "easy" as it's not a true maths problem, which I found on facebook earlier today. It's a kind of find the minimal route problem.
The objective is to travel only on one or two digit Interstate routes, making ones way from one side of the US to the other. Thus you start on I-5 and end up on I-95. Also when you change from one interstate to another you can only move onto a higher numbered one; the "cost" of making this move is the square of the difference. The objective is to find the "minimal cost" route.
As an example, obviously not the best route, you could go 5 - 10 - 15 - 90 - 95 the cost would be 25+25+5625+25 = 5700. A route such as 5 - 8 -10 - 55 - 90 - 95 would be better (9+4+2025+1225+25=3288).
btw I've only just heard about the problem so don't know the answer and here it's Bank Holiday weekend, so will look at it later! Personally I'll be assuming the wiki entries for interstates is correct.
https://en.wikipedia.org/wiki/Interstate_55 (you can enter the various numbers)
https://gisgeography.com/wp-content/uploads/2020/07/US-Road-Map.pdf (I don't know how accurate this is, but it is useful to see the direction of roads and which ones will never get near somewhere interesting, such as 19, 27 etc.)
https://www.visualcapitalist.com/wp-content/uploads/2017/10/us-interstates-as-a-subway-map.jpg
link to original post
Assuming we are traveling from the Atlantic to the Pacific, or vice versa, then I-5 and I-95 wonít work, as most odd-numbered highways travel north-south, and most even-numbered highways travel east-west. Going strictly by memory, I believe 1-80 goes from San Francisco (West Coast) to New Jersey (East Coast). Possibly better still is I-10, which starts about as close as you can drive to the water (aside from non-highway parking lots) in Santa Monica, CA. Unfortunately, I am unfamiliar with the other endÖ
As has been said, there are many E-W routes that can make that trip immediately, but the puzzle is to minimise the "cost" (square of the difference) using increasingly numbered interstate roads. That's why from i5 to i10, it's better to use i5 i8 i10. Similarly, at the end, there's also a better (mathematical) route than just i90 to i95.
Edit: I went down on one for geographical purposes, so I guess that's no good. So I tried it again and got 2072.
Good try, interesting as I can see the route you probably usedQuote: AutomaticMonkey...got 2072...
5
8
10
20
30
40
55
57
64
65
70
77
80
84
90
95
Sum of differences squared is 762
Quote: charliepatrickGood try, interesting as I can see the route you probably used [...but you need to add more routes in the middle. I've got less than a half of your figure.Quote: AutomaticMonkey...got 2072...
link to original post
Maybe I'll get a slime mold to help me. Experiments have shown them to be good at routing.
Edit: I'm also doing what most people would intuitively do, thinking of it first as a travel problem and not a math problem. The actual lowest number would surely be nothing like a route anyone would practically take.
| Interstate | from Start | |
|---|---|---|
5 | 0 | |
8 | 9 | 5 |
10 | 13 | 5 8 |
20 | 113 | 5 8 10 20 |
30 | 213 | 5 8 10 20 30 |
35 | 238 | 5 8 10 20 30 35 |
40 | 263 | 5 8 10 20 30 35 40 |
44 | 279 | 5 8 10 20 30 35 44 |
55 | 400 | 5 Ö 20 55 |
64 | 481 | Ö. 44 64 |
65 | 482 | Ö. 64 65 |
69 | 498 | Ö. 65 69 |
70 | 499 | Ö. 65 69 70 |
74 | 515 | Ö. 70 74 |
75 | 516 | Ö. 70 74 75 |
80 | 541 | Ö. 70 74 75 80 |
81 | 542 | ,,,, 80 81 |
84 | 551 | Ö. 81 84 |
87 | 560 | Ö 84 87 |
90 | 569 | Ö. 87 90 |
91 | 570 | Ö. 90 91 |
93 | 574 | Ö. 90 91 93 |
95 | 578 |
Note: I'm not sure whether it's allowed to use the Indianapolis ring road twice for different interstates, if not then it would be reasonable to miss 74 and go 65, 69-ring road, 70, 75.
A rough estimate is 2.5 * 1.35^(log2(n) - 1) for an n-sided die. Log2 meaning base 2 logQuote: WizardQuote: ThatDonGuy
For N-sided dice from 2 to 20, I get these fractions:
2: 5 / 2
3: 26 / 9
4: 103 / 32
5: 2,194 / 625
6: 1,223 / 324
7: 472,730 / 117,649
8: 556,403 / 131,072
9: 21,323,986 / 4,782,969
10: 7,281,587 / 1,562,500
11: 125,858,034,202 / 25,937,424,601
12: 180,451,625 / 35,831,808
13: 121,437,725,363,954 / 23,298,085,122,481
14: 595,953,719,897 / 110,730,297,608
15: 26,649,932,810,926 / 4,805,419,921,875
16: 3,211,211,914,492,699 / 562,949,953,421,312
17: 285,050,975,993,898,158,530 / 48,661,191,875,666,868,481
18: 549,689,343,118,061 / 91,507,169,819,844
19: 640,611,888,918,574,971,191,834 / 104,127,350,297,911,241,532,841
20: 4,027,894,135,040,576,041 / 640,000,000,000,000,000
I am trying to find a formula, but so far it has eluded me
link to original post
I agree with your values for 6- and 20-sided dice, the only ones I worked out that you did. For a 100-sided die, I get 13.20996063.
I too have failed at finding a simple formula for even an estimate. It came to me later this is similar to the common birthday problem. As far as I know, nobody has come up with a handy formula for the probability of a common birthday among n people.
link to original post
Wikipedia claims Srinivasa Ramanujan has solved this for the birthday problems (n=365) via asymptotic expansion. I should edit the Wikipedia article and add my exact solution via integral of (((x/365)+ 1) / e^(x/365))^365 dx
Birthday problems are normally formatted as the chance of at least one match in a given sample size. Thatís a much easier problem than average number of people needed for first match
Quote: Ace2A rough estimate is 2.5 * 1.35^(log2(n) - 1) for an n-sided die. Log2 meaning base 2 logQuote: WizardQuote: ThatDonGuy
For N-sided dice from 2 to 20, I get these fractions:
2: 5 / 2
3: 26 / 9
4: 103 / 32
5: 2,194 / 625
6: 1,223 / 324
7: 472,730 / 117,649
8: 556,403 / 131,072
9: 21,323,986 / 4,782,969
10: 7,281,587 / 1,562,500
11: 125,858,034,202 / 25,937,424,601
12: 180,451,625 / 35,831,808
13: 121,437,725,363,954 / 23,298,085,122,481
14: 595,953,719,897 / 110,730,297,608
15: 26,649,932,810,926 / 4,805,419,921,875
16: 3,211,211,914,492,699 / 562,949,953,421,312
17: 285,050,975,993,898,158,530 / 48,661,191,875,666,868,481
18: 549,689,343,118,061 / 91,507,169,819,844
19: 640,611,888,918,574,971,191,834 / 104,127,350,297,911,241,532,841
20: 4,027,894,135,040,576,041 / 640,000,000,000,000,000
I am trying to find a formula, but so far it has eluded me
link to original post
I agree with your values for 6- and 20-sided dice, the only ones I worked out that you did. For a 100-sided die, I get 13.20996063.
I too have failed at finding a simple formula for even an estimate. It came to me later this is similar to the common birthday problem. As far as I know, nobody has come up with a handy formula for the probability of a common birthday among n people.
link to original post
Wikipedia claims Srinivasa Ramanujan has solved this for the birthday problems (n=365) via asymptotic expansion. I should edit the Wikipedia article and add my exact solution via integral of (((x/365)+ 1) / e^(x/365))^365 dx
Birthday problems are normally formatted as the chance of at least one match in a given sample size. Thatís a much easier problem than average number of people needed for first match
link to original post
Well, I get this:
The value is:
2
+ (N-1) / N
+ (N-1) / N x (N-2) / N
+ (N-1) / N x (N-2) / N x (N-3) / N
+ ...
+ (N-1) / N x (N-2) / N x (N-3) / N x ... x 2 / N
+ (N-1) / N x (N-2) / N x (N-3) / N x ... x 2 / N x 1 / N
This is the sum of:
2
(N-1)! / (0! N^((N-1)-0)
(N-1)! / (1! N^((N-1)-1)
(N-1)! / (2! N^((N-1)-2)
...
(N-1)! / ((N-3)! N^((N-1)-(N-3)))
(N-1)! / ((N-2)! N^((N-1)-(N-2)))
which is the sum of:
2
N (N-1)! / (0! N^(N-1))
N^2 (N-1)! / (1! N^(N-1))
N^3 (N-1)! / (2! N^(N-1))
...
N^(N-2) (N-1)! / ((N-3)! N^(N-1))
N^(N-1) (N-1)! / ((N-2)! N^(N-1))
which is 2 + N (N-1)! / N^(N-1) times the sum of:
1 / 0!
N / 1!
N^2 / 2!
...
N^(N-2) / (N-2)!
This is the first N-1 terms of the Taylor expansion for e^N, so the sum approximates to 2 + (N-1)! e^N / N^(N-2)
How is that estimate related to the answer? For N=20 your formula gives 227.14 vs the answer of 6.29Quote: ThatDonGuyQuote: Ace2A rough estimate is 2.5 * 1.35^(log2(n) - 1) for an n-sided die. Log2 meaning base 2 logQuote: WizardQuote: ThatDonGuy
For N-sided dice from 2 to 20, I get these fractions:
2: 5 / 2
3: 26 / 9
4: 103 / 32
5: 2,194 / 625
6: 1,223 / 324
7: 472,730 / 117,649
8: 556,403 / 131,072
9: 21,323,986 / 4,782,969
10: 7,281,587 / 1,562,500
11: 125,858,034,202 / 25,937,424,601
12: 180,451,625 / 35,831,808
13: 121,437,725,363,954 / 23,298,085,122,481
14: 595,953,719,897 / 110,730,297,608
15: 26,649,932,810,926 / 4,805,419,921,875
16: 3,211,211,914,492,699 / 562,949,953,421,312
17: 285,050,975,993,898,158,530 / 48,661,191,875,666,868,481
18: 549,689,343,118,061 / 91,507,169,819,844
19: 640,611,888,918,574,971,191,834 / 104,127,350,297,911,241,532,841
20: 4,027,894,135,040,576,041 / 640,000,000,000,000,000
I am trying to find a formula, but so far it has eluded me
link to original post
I agree with your values for 6- and 20-sided dice, the only ones I worked out that you did. For a 100-sided die, I get 13.20996063.
I too have failed at finding a simple formula for even an estimate. It came to me later this is similar to the common birthday problem. As far as I know, nobody has come up with a handy formula for the probability of a common birthday among n people.
link to original post
Wikipedia claims Srinivasa Ramanujan has solved this for the birthday problems (n=365) via asymptotic expansion. I should edit the Wikipedia article and add my exact solution via integral of (((x/365)+ 1) / e^(x/365))^365 dx
Birthday problems are normally formatted as the chance of at least one match in a given sample size. Thatís a much easier problem than average number of people needed for first match
link to original post
Well, I get this:
The value is:
2
+ (N-1) / N
+ (N-1) / N x (N-2) / N
+ (N-1) / N x (N-2) / N x (N-3) / N
+ ...
+ (N-1) / N x (N-2) / N x (N-3) / N x ... x 2 / N
+ (N-1) / N x (N-2) / N x (N-3) / N x ... x 2 / N x 1 / N
This is the sum of:
2
(N-1)! / (0! N^((N-1)-0)
(N-1)! / (1! N^((N-1)-1)
(N-1)! / (2! N^((N-1)-2)
...
(N-1)! / ((N-3)! N^((N-1)-(N-3)))
(N-1)! / ((N-2)! N^((N-1)-(N-2)))
which is the sum of:
2
N (N-1)! / (0! N^(N-1))
N^2 (N-1)! / (1! N^(N-1))
N^3 (N-1)! / (2! N^(N-1))
...
N^(N-2) (N-1)! / ((N-3)! N^(N-1))
N^(N-1) (N-1)! / ((N-2)! N^(N-1))
which is 2 + N (N-1)! / N^(N-1) times the sum of:
1 / 0!
N / 1!
N^2 / 2!
...
N^(N-2) / (N-2)!
This is the first N-1 terms of the Taylor expansion for e^N, so the sum approximates to 2 + (N-1)! e^N / N^(N-2)
link to original post
Quote: Ace2How is that estimate related to the answer? For N=20 your formula gives 227.14 vs the answer of 6.29Quote: ThatDonGuyQuote: Ace2A rough estimate is 2.5 * 1.35^(log2(n) - 1) for an n-sided die. Log2 meaning base 2 logQuote: WizardQuote: ThatDonGuy
For N-sided dice from 2 to 20, I get these fractions:
2: 5 / 2
3: 26 / 9
4: 103 / 32
5: 2,194 / 625
6: 1,223 / 324
7: 472,730 / 117,649
8: 556,403 / 131,072
9: 21,323,986 / 4,782,969
10: 7,281,587 / 1,562,500
11: 125,858,034,202 / 25,937,424,601
12: 180,451,625 / 35,831,808
13: 121,437,725,363,954 / 23,298,085,122,481
14: 595,953,719,897 / 110,730,297,608
15: 26,649,932,810,926 / 4,805,419,921,875
16: 3,211,211,914,492,699 / 562,949,953,421,312
17: 285,050,975,993,898,158,530 / 48,661,191,875,666,868,481
18: 549,689,343,118,061 / 91,507,169,819,844
19: 640,611,888,918,574,971,191,834 / 104,127,350,297,911,241,532,841
20: 4,027,894,135,040,576,041 / 640,000,000,000,000,000
I am trying to find a formula, but so far it has eluded me
link to original post
I agree with your values for 6- and 20-sided dice, the only ones I worked out that you did. For a 100-sided die, I get 13.20996063.
I too have failed at finding a simple formula for even an estimate. It came to me later this is similar to the common birthday problem. As far as I know, nobody has come up with a handy formula for the probability of a common birthday among n people.
link to original post
Wikipedia claims Srinivasa Ramanujan has solved this for the birthday problems (n=365) via asymptotic expansion. I should edit the Wikipedia article and add my exact solution via integral of (((x/365)+ 1) / e^(x/365))^365 dx
Birthday problems are normally formatted as the chance of at least one match in a given sample size. Thatís a much easier problem than average number of people needed for first match
link to original post
Well, I get this:
The value is:
2
+ (N-1) / N
+ (N-1) / N x (N-2) / N
+ (N-1) / N x (N-2) / N x (N-3) / N
+ ...
+ (N-1) / N x (N-2) / N x (N-3) / N x ... x 2 / N
+ (N-1) / N x (N-2) / N x (N-3) / N x ... x 2 / N x 1 / N
This is the sum of:
2
(N-1)! / (0! N^((N-1)-0)
(N-1)! / (1! N^((N-1)-1)
(N-1)! / (2! N^((N-1)-2)
...
(N-1)! / ((N-3)! N^((N-1)-(N-3)))
(N-1)! / ((N-2)! N^((N-1)-(N-2)))
which is the sum of:
2
N (N-1)! / (0! N^(N-1))
N^2 (N-1)! / (1! N^(N-1))
N^3 (N-1)! / (2! N^(N-1))
...
N^(N-2) (N-1)! / ((N-3)! N^(N-1))
N^(N-1) (N-1)! / ((N-2)! N^(N-1))
which is 2 + N (N-1)! / N^(N-1) times the sum of:
1 / 0!
N / 1!
N^2 / 2!
...
N^(N-2) / (N-2)!
This is the first N-1 terms of the Taylor expansion for e^N, so the sum approximates to 2 + (N-1)! e^N / N^(N-2)
link to original post
link to original post
That's a good question...
Those terms where it says "This is the sum of..." the first time look wrong.
The answer is 2 + (N-1)! / N times the sum of:
1 / (N-2)!
1 / (N (N-3)!)
1 / (N^2 (N-4)!)
...
1 / (N^(N-3) (N-(N-1))!)
1 / (N^(N-2) (N-N)!)
I am trying to work out an approximation for this
A fair die is rolled until it lands on a 6. A player will win the square in dollars of the number of rolls required. What is the expected win?
Quote: charliepatrickObviously I knocked up a spreadsheet but sense someone knows the best route to how integrals can be created for these types of things (I've never quite worked them out).
Spreadsheet gives 66.
link to original post
I agree with your answer.
Quote: WizardThe following problem is a variant of this one. Unless you pull a formula out of your pocket or use a spreadsheet, I think you'll find it pretty challenging to prove your answer.
A fair die is rolled until it lands on a 6. A player will win the square in dollars of the number of rolls required. What is the expected win?
link to original post
This is the sum of:
1/6 x 1^2
1/6 x 5/6 x 2^2
1/6 x (5/6)^2 x 3^2
...
which is
1/6 x (1^2 + 5/6 x 2^2 + (5/6)^2 x 3^2 + ...)
= 1/6 (5/6 + 1) / (1 - 5/6)^3
= 216 x 11/36 = 66
Click Here for the proof that 1^2 + p 2^2 + p^2 3^2 + p^3 4^2 + ... = (p + 1) / (1 - p)^3; click on the "Click Here for Math" button on that post
Quote: ThatDonGuy
This is the sum of:
1/6 x 1^2
1/6 x 5/6 x 2^2
1/6 x (5/6)^2 x 3^2
...
which is
1/6 x (1^2 + 5/6 x 2^2 + (5/6)^2 x 3^2 + ...)
= 1/6 (5/6 + 1) / (1 - 5/6)^3
= 216 x 11/36 = 66
Click Here for the proof that 1^2 + p 2^2 + p^2 3^2 + p^3 4^2 + ... = (p + 1) / (1 - p)^3; click on the "Click Here for Math" button on that post
link to original post
I, of course, agree.
I got at the answer a bit differently. Here is how (PDF).
As stated in my earlier post, the calculation is the same for the discrete case with probability 1/p though you must reduce it by p. Therefore the answer to this problem is 6^2 * 2! - 6 which can also be obtained by integrating 1/e^(x/6)*1/6*x^2 dx from zero to infinity and then subtracting 6 for the answer of 66
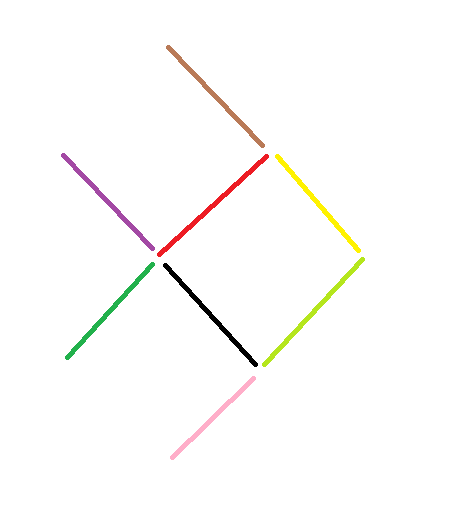
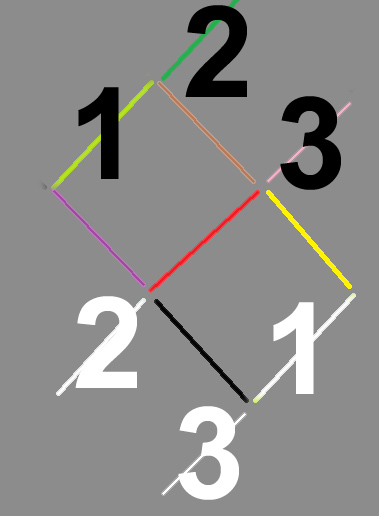
Make the fish point the opposite direction by moving three toothpicks only.
Quote: charliepatrick
link to original post
I agree!


