Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
June 16th, 2025 at 11:15:17 AM
permalink
Quote: ThatDonGuy
To 100 places, I get:
0.14015 01597 77671 70675 03301 99764 58363 24852 96210 37282 37474 09380 11959 51720 40943 79197 71682 53488 94282 64038
link to original post
I agree.
June 26th, 2025 at 6:48:47 PM
permalink
I've done a quick spreadsheet which looks at all the permutaions of 6-13 (i.e. 8*8*8*8) and assumes there are only 4 of each rank. However a trick I've used (see 6 6 7 6 where there's a tie) is to divide the 96 ways to get it, so each of the winners have 48 wins each. This is why the total includes 2/3 as there can be 3-way ties.
I haven't checked anything but it shouldn't take long to knock up a similar spreadsheet.
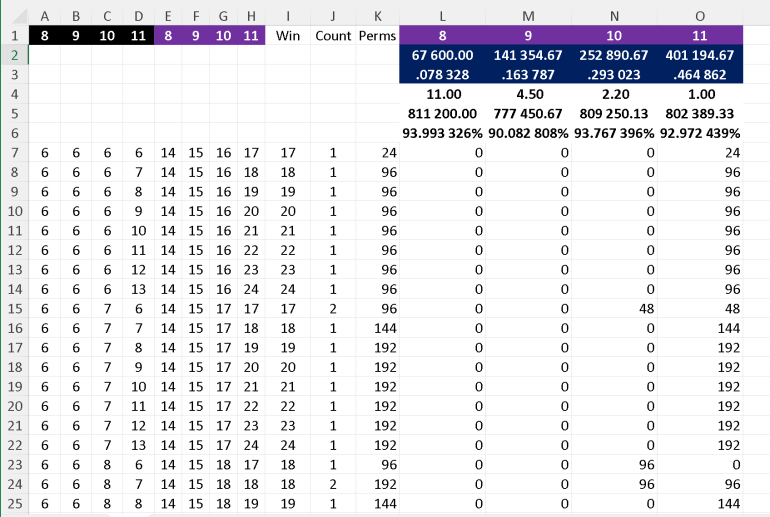
I haven't checked anything but it shouldn't take long to knock up a similar spreadsheet.

June 26th, 2025 at 8:43:55 PM
permalink
Quote: charliepatrickI've done a quick spreadsheet
link to original post
We're pretty close, but not quite in agreement. Probably something to do with the ties. My figures are the page I linked to.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 27th, 2025 at 4:52:23 AM
permalink
I'm pretty sure the error is on my end, but I can't find it.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 27th, 2025 at 5:56:58 AM
permalink
I found it. Stupid mistake, as usual. I definitely owe you a beer for this one.
Updated table.
Updated table.
| Winner | Pays | Probability | Return |
|---|---|---|---|
| 8 | 11 | 0.078328 | -0.060067 |
| 9 | 4.5 | 0.163787 | -0.099172 |
| 10 | 2.2 | 0.293023 | -0.062326 |
| 11 | 1 | 0.464862 | -0.070276 |
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 28th, 2025 at 4:39:24 PM
permalink
No mention of ties? e. g., deck composition KQKQKKQQJJJJTTTT9999888877776666. I think there might be over two trillion deck permutations resulting in a tie. I was working on a finite proof with Python programming that was easy peasy for the initial deal, but bogged down as I worked to resolve ties. On reasoning how far must be gone and how often, I see why my laptop does not have the horsepower for that type of solution. (Edit: revised estimate from one to two trillion.)
“You don’t bring a bone saw to a negotiation.” - Robert Jordan, former U.S. ambassador to Saudi Arabia
June 29th, 2025 at 2:45:51 AM
permalink
Quote: BleedingChipsSlowlyNo mention of ties?
link to original post
Once the game gets to a tie, it becomes a coin flip.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 29th, 2025 at 3:17:18 AM
permalink
The number of different orders of 32 cards ignoring the suits is 32!/(4!)8, about 2.4*1024. Even if a few trillion of them result in a tie, the probability is tiny.
June 30th, 2025 at 11:06:28 AM
permalink
Here are some belated Easy Monday puzzles...

The U.S. debt is measured in trillions of dollars.
Could a New York Times reporter have written about this story one trillion seconds ago?

As seen from the surface of earth, the sun and the moon appear to be the same size. The sun is actually 400 times larger than the moon.
How far away from earth is the sun compared to how far away the moon is?
%2Fpic148345.jpg&f=1&ipt=c26ce95d0258ba6b7cadd6064529d544cc40f79af89e03c90b11d0cf575dcf24)
The board game Magic Realm has an unusual dice mechanic. Two standard six-sided dice are rolled, but only the higher of the two numbers acts as the result.
For example:
A 1-6 would = 6
A 3-4 would = 4
A 2-2 would = 2
What is the probability of getting a result of 5?

The U.S. debt is measured in trillions of dollars.
Could a New York Times reporter have written about this story one trillion seconds ago?
As seen from the surface of earth, the sun and the moon appear to be the same size. The sun is actually 400 times larger than the moon.
How far away from earth is the sun compared to how far away the moon is?
%2Fpic148345.jpg&f=1&ipt=c26ce95d0258ba6b7cadd6064529d544cc40f79af89e03c90b11d0cf575dcf24)
The board game Magic Realm has an unusual dice mechanic. Two standard six-sided dice are rolled, but only the higher of the two numbers acts as the result.
For example:
A 1-6 would = 6
A 3-4 would = 4
A 2-2 would = 2
What is the probability of getting a result of 5?
Have you tried 22 tonight? I said 22.
June 30th, 2025 at 11:19:15 AM
permalink
1. No. That comes to 31,710 years. I doubt there was a concept or term for numbers that big back then. Interesting thought.
2. If "size" is measured as volume, then I get 40^(1/3) =~ 7.368 times as far away.
3. 9/36 = 1/4.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 30th, 2025 at 11:51:30 AM
permalink
Quote: Wizard
1. No. That comes to 31,710 years. I doubt there was a concept or term for numbers that big back then. Interesting thought.
2. If "size" is measured as volume, then I get 40^(1/3) =~ 7.368 times as far away.
3. 9/36 = 1/4.
link to original post
2. Not volume but diameter. (Think solar eclipse.)
It's very easy Monday.
Have you tried 22 tonight? I said 22.
June 30th, 2025 at 3:38:57 PM
permalink
Quote: GialmereHere are some belated Easy Monday puzzles...
link to original post
Time: there are 86,400 < 100,000 seconds per day, and 365.25 or so < 400 days per year, so there are < 40 million seconds per year, which means there are < 40 million x 25,000, or < 1 trillion, seconds in 25,000 years. Since the NYT was not around 25,000 years ago, it could not have reported on anything 1 trillion seconds ago.
Space: assuming the diameter of the sun is 400 times the diameter of the moon, it must be 400 times as far from Earth as the moon in order for the two to appear to be the same size. Think of the diameter of each as the far end of an isosceles triangle; you have two similar triangles.
Dice: of the 36 possible rolls of 2 dice, 11 of them (1-5 through 4-5, and 5-1 through 5-5) have the highest number 5, so the probability is 11/36.
Side note: you would think that, given how many games printed by the old Avalon Hill Game Company have been reprinted by other companies since its demise around 25 years ago, this one would have been reprinted at least once, but it has not.


