Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
July 30th, 2020 at 4:30:46 PM
permalink
Hint: it's not by spamming 10 different threads with the same question.
July 30th, 2020 at 4:40:57 PM
permalink
Quote: charliepatrickLet's assume the candles were originally 12" tall. So the large one (L) burns at 3" per hour, and the small one (S) at 4" per hour.
After 2 hours L has lost 6" so has 6" left; S has lost 8" so has 4" left. After 3 hours L has lost 9" so has 3" left, S has now just burnt out.
So let t be the time before 3 hours. The height of the large one is L=3+3t, the height of the small one is S=4t.
At the time of the solution L=2S.
So 8t=3+3t; 5t=3, t=3/5.
So after 2 2/5 hour...
...the large candle is 12-(2.4*3) = 12-7.2 = 4.8" tall
...the small candle is 12-(2.4*4) = 12-9.6 = 2.4" tall.
So the time is 2 hours 24 minutes.
Quote: Wizard
I see I agree with Charlie, but I want to get credit anyway...
Let:
a = Time remaining on thick candle
b = Time remaining on thin candle
t = Time candle burned.
a = 4-t
b = 3-t
The height of each candle will be proportional to it's remaining time to it's beginning time.
Ratio of height left of a = (4-t)/4
Ratio of height left of b = (3-t)/3
Let's say each candle starts at 12". At some time x, the thick one will be twice as tall. In other words,
12*((4-t)/4) = 2*12*((3-t)/3)
3 * (4-t) = 8 * (3-t)
12 - 3t = 24 - 8t
5t = 12
t = 2.4
So, the candles have burned for 2.4 hours.
Good puzzle.
Correct!
----------------------------
My wife said if I bought her one more stupid gift she would burn it.
So I bought her a candle.
Have you tried 22 tonight? I said 22.
July 30th, 2020 at 5:26:31 PM
permalink
Speaking of candles.
You have a box of matches and six 64-minute candles. Candles may burn from either or both ends. Each candle burns exactly 64 minutes but the rate of burning is inconsistent. A half a candle would not necessarily burn in 32 minutes. The candles are also not equally inconsistent. Two cut candles of the same length would not necessarily burn in the same time. Without the use of a clock, scissors, or anything other than the matches and the candles how can you create a 60-minute candle?
You have a box of matches and six 64-minute candles. Candles may burn from either or both ends. Each candle burns exactly 64 minutes but the rate of burning is inconsistent. A half a candle would not necessarily burn in 32 minutes. The candles are also not equally inconsistent. Two cut candles of the same length would not necessarily burn in the same time. Without the use of a clock, scissors, or anything other than the matches and the candles how can you create a 60-minute candle?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 30th, 2020 at 5:50:41 PM
permalink
Deleted
It’s all about making that GTA
July 30th, 2020 at 5:52:23 PM
permalink
Do you need 6? I can do it with 5
Label five of the candles A, B, C, D, and E
Light both ends of candle A, and one end of candles B, C, and D
32 minutes later, candle A is extinguished, and B, C, and D have 32 minutes left; light the other end of candle B
16 minutes later, candle B is extinguished, and C and D have 16 minutes left; light the other end of candle C
8 minutes later, candle C is extinguished, and D has 8 minutes left; light the other end of candle D, and one end of candle E
4 minutes later, candle D is extinguished; extinguish candle E, which is now a 60-minute candle
July 31st, 2020 at 1:58:18 AM
permalink
Don, you seem to be right, you do need only five. Well done.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
August 1st, 2020 at 8:26:29 PM
permalink
Starting with a new shooter’s first roll, what the expected number of rolls to resolve the fire bet (all six points)?
It’s all about making that GTA
August 1st, 2020 at 8:56:30 PM
permalink
Quote: Ace2Starting with a new shooter’s first roll, what the expected number of rolls to resolve the fire bet (all six points)?
Do you mean to win the Fire Bet?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
August 1st, 2020 at 10:17:35 PM
permalink
To resolve it. To win or lose it. Must be all six points to winQuote: WizardDo you mean to win the Fire Bet?
A recent thread basically asked what’s the lowest edge (per roll) wager on the table. Though technically the fire bet probably doesn’t qualify, it got me thinking what the edge per roll might be.
It’s all about making that GTA
August 2nd, 2020 at 1:57:08 AM
permalink
On your rotating dice image, I am never seeing the number 3. Am I missing something lol?
August 2nd, 2020 at 8:22:59 AM
permalink
Quote: Ace2To resolve it. To win or lose it. Must be all six points to win
I'll see if I can work up a computed solution later today. It's not quite as easy as it sounds, as you have to take into account the re-rolling of earlier points.
For example, if, e.g., E{6,8} means the expected number once you have already made the 6 and 8, then E{4,5,6} is the sum of:
1 -- the next roll
1/3 x E{4,5,6} -- rolling a natural or craps
1/12 x 2/3 x (the expected number of rolls to miss a point of 4)
1/12 x 1/3 x (the expected number of rolls to make a point of 4) x E{4,5,6}
1/9 x 3/4 x (the expected number of rolls to miss a point of 5)
1/9 x 1/4 x (the expected number of rolls to make a point of 5) x E{4,5,6}
5/36 x 6/11 x (the expected number of rolls to miss a point of 6)
5/36 x 5/11 x (the expected number of rolls to make a point of 6) x E{4,5,6}
5/36 x 6/11 x (the expected number of rolls to miss a point of 8)
5/36 x 5/11 x (the expected number of rolls to make a point of 8) x E{4,5,6,8}
1/9 x 3/4 x (the expected number of rolls to miss a point of 9)
1/9 x 1/4 x (the expected number of rolls to make a point of 9) x E{4,5,6.9}
1/12 x 2/3 x (the expected number of rolls to miss a point of 10)
1/12 x 1/3 x (the expected number of rolls to make a point of 10) x E{4,5,6,10}
August 2nd, 2020 at 9:50:03 AM
permalink
Quote: Ace2Starting with a new shooter’s first roll, what the expected number of rolls to resolve the fire bet (all six points)?
I think this not an "easy" problem. That said, here is my ...
8.52412536496924
As a reality check, the expected rolls per shooter is 8.52551020408163, which should be a little more, as the player will still keep shooting after winning the Fire bet.
The difference is 0.00138483911240.
It can be found on my site the probability of winning the Fire Bet is 0.000162435.
0.00138483911240/0.000162435 = 8.52551020408163.
This makes sense as if the player wins the Fire Bet, he can expect to roll the same number of times from that point as a fresh shooter.
I probably should have done it that way to begin with, but I did it from scratch with a Markov Chain. Yes, next I'll do it with an integral, as soon as I figure out how to set it up properly.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
August 2nd, 2020 at 10:32:04 AM
permalink
As a rational number, I get 1,812,411,430,047,906,383,008,275,074,367,503,120,787,919,877 / 212,621,395,445,003,244,039,537,720,489,806,989,098,501,552
This is about 8.524, which is in line with simulation.
August 2nd, 2020 at 2:31:56 PM
permalink
Quote: ThatDonGuy
As a rational number, I get 1,812,411,430,047,906,383,008,275,074,367,503,120,787,919,877 / 212,621,395,445,003,244,039,537,720,489,806,989,098,501,552
This is about 8.524, which is in line with simulation.
You can use my Calculator to solve that fraction to about 200 decimal places.
It gives and answer of ...
8.524125364969235306716226354263265894844054830893892380461387183547919960879226601357329869160257663444176437649024965837412598384033096488651707166597741954157645984860065445620151460834281272750147688402872739349839291833042135572671058657848177493067744
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
August 2nd, 2020 at 3:17:31 PM
permalink
What surprised me the most about this was, the expected number of rolls needed to resolve a point of 4 (or 10), the expected number needed to make a point of 4, and the expected number to miss a point of 4, are all the same (4), and that the same applies for points of 5/9 (3.6) and 6/8 (36/11).
August 2nd, 2020 at 3:21:07 PM
permalink
Congratulations Wizard. That’s the correct answer
Since we already know the average roll length L of a shooters turn and the probability P of winning the fire bet, we can say that R + PL = L, where R is avg rolls to resolve the fire bet. Solve for R to get 8.524125 rolls. I think that qualifies as an easy puzzle.
Or take the integral over all time of this to get the same answer
e^(-196x/1671)*(1-((1-e^(-125x/6684))*(1-e^(-22x/1671))*(1-e^(-55x/6684)))^2) dx
1671/196 is average rolls for a seven out
6664/125 is average rolls for winning an 8
1671/22 is average rolls for winning a 9
6684/55 is average rolls for winning a 10
Exact answer
1812411430047906383008275074367503120787919877
/212621395445003244039537720489806989098501552
Since we already know the average roll length L of a shooters turn and the probability P of winning the fire bet, we can say that R + PL = L, where R is avg rolls to resolve the fire bet. Solve for R to get 8.524125 rolls. I think that qualifies as an easy puzzle.
Or take the integral over all time of this to get the same answer
e^(-196x/1671)*(1-((1-e^(-125x/6684))*(1-e^(-22x/1671))*(1-e^(-55x/6684)))^2) dx
1671/196 is average rolls for a seven out
6664/125 is average rolls for winning an 8
1671/22 is average rolls for winning a 9
6684/55 is average rolls for winning a 10
Exact answer
1812411430047906383008275074367503120787919877
/212621395445003244039537720489806989098501552
It’s all about making that GTA
August 2nd, 2020 at 4:05:02 PM
permalink
Quote: Ace2Since we already know the average roll length L of a shooters turn and the probability P of winning the fire bet, we can say that R + PL = L, where R is avg rolls to resolve the fire bet. Solve for R to get 8.524125 rolls. I think that qualifies as an easy puzzle.
So "the expected length of a shooter's run = the expected length of a fire bet + (the probability of winning a fire bet x the expected length of a shooter's run)."
That does not seem intuitive. Could you explain the reasoning?
It can also be expressed as "the expected length of a fire bet = the expected length of a shooter's run x the probability of losing a fire bet" (R = L - PL = L (1 - P)).
August 2nd, 2020 at 5:13:49 PM
permalink
Thinking in terms of average total rolls per shooter L:
New shooter rolls R times until there’s a resolution of the fire bet (sixth point won or seven-out, whichever comes first). There’s a 1-P chance that the resolution was a seven-out and his turn is over...so no more rolls. There’s a P chance that the resolution was a fire bet win. In that case the shooter starts another come out roll with L rolls.
So R + PL = L
That’s not intuitive?
New shooter rolls R times until there’s a resolution of the fire bet (sixth point won or seven-out, whichever comes first). There’s a 1-P chance that the resolution was a seven-out and his turn is over...so no more rolls. There’s a P chance that the resolution was a fire bet win. In that case the shooter starts another come out roll with L rolls.
So R + PL = L
That’s not intuitive?
It’s all about making that GTA
August 2nd, 2020 at 5:32:20 PM
permalink
Thinking out loud.
Probability fire bet wins
Integral: 1-(1-exp(-x/24))^2*(1-exp(-x/15))^2*(1-exp(-25*x/264))^2
Integral calculator
Expected rolls to achieve every point at least once = integral of 1-(1-exp(-x/36))^2*(1-exp(-2*x/45))^2*(1-exp(-25*x/396))^2 = 64.91860341630701 rolls. I'm not sure if that is right. Next step is to introduce the 7-out as a stopping event.
Probability fire bet wins
Integral: 1-(1-exp(-x/24))^2*(1-exp(-x/15))^2*(1-exp(-25*x/264))^2
Integral calculator
Expected rolls to achieve every point at least once = integral of 1-(1-exp(-x/36))^2*(1-exp(-2*x/45))^2*(1-exp(-25*x/396))^2 = 64.91860341630701 rolls. I'm not sure if that is right. Next step is to introduce the 7-out as a stopping event.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
August 2nd, 2020 at 5:58:53 PM
permalink
Quote: Ace2Thinking in terms of average total rolls per shooter L:
New shooter rolls R times until there’s a resolution of the fire bet (sixth point won or seven-out, whichever comes first). There’s a 1-P chance that the resolution was a seven-out and his turn is over...so no more rolls. There’s a P chance that the resolution was a fire bet win. In that case the shooter starts another come out roll with L rolls.
So R + PL = L
That’s not intuitive?
Well, when you put it that way...
August 3rd, 2020 at 8:35:53 AM
permalink
Quote: Ace2Congratulations Wizard. That’s the correct answer
Thank you.
Quote:Since we already know the average roll length L of a shooters turn and the probability P of winning the fire bet, we can say that R + PL = L, where R is avg rolls to resolve the fire bet. Solve for R to get 8.524125 rolls. I think that qualifies as an easy puzzle.
Or take the integral over all time of this to get the same answer
e^(-196x/1671)*(1-((1-e^(-125x/6684))*(1-e^(-22x/1671))*(1-e^(-55x/6684)))^2) dx
1671/196 is average rolls for a seven out
6664/125 is average rolls for winning an 8
1671/22 is average rolls for winning a 9
6684/55 is average rolls for winning a 10
Exact answer
1812411430047906383008275074367503120787919877
/212621395445003244039537720489806989098501552
I just finished my calculus solution and agree with the above. Definitely not an "easy" problem. I prefer to express the integral as e^(-196x/1671)*(1-(1-e^(-125x/6684))^2*(1-e^(-22x/1671))^2*(1-e^(-55x/6684))^2).
Last edited by: Wizard on Aug 3, 2020
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
August 3rd, 2020 at 10:00:07 AM
permalink
Here’s an easy one.
Starting with a new shooter, what’s the expected number of rolls to win the fire bet ? The winner doesn’t have to be that shooter
Starting with a new shooter, what’s the expected number of rolls to win the fire bet ? The winner doesn’t have to be that shooter
It’s all about making that GTA
August 3rd, 2020 at 10:20:28 AM
permalink
Integral from 0 to infinity of (1-(1-e^(-125x/6684))^2*(1-e^(-22x/1671))^2*(1-e^(-55x/6684))^2) = apx. 219.1494672902
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
August 3rd, 2020 at 10:34:25 AM
permalink
Quote: Wizard
Integral from 0 to infinity of (1-(1-e^(-125x/6684))^2*(1-e^(-22x/1671))^2*(1-e^(-55x/6684))^2) = apx. 219.1494672902
219 rolls for a bet that has about a 1 in 6,000 chance of winning ?
It’s all about making that GTA
August 3rd, 2020 at 10:52:22 AM
permalink
Quote: Ace2Here’s an easy one.
Starting with a new shooter, what’s the expected number of rolls to win the fire bet ? The winner doesn’t have to be that shooter
Somewhere around 52,477; it's the expected number of rolls to resolve a fire bet divided by the probability of winning
Let E be the number needed for the current shooter to win or lose the Fire Bet, and P the probability of a shooter winning the Fire Bet
First shooter wins: EP
Second shooter wins: (1-P) P x 2E
Third shooter wins: (1-P)^2 P x 3E
...
Sum = EP (1 + 2 (1-P) + 3 (1-P)^2 + ...)
= EP (1 + (1-P) + (1-P)^2 + ...)^2
= EP / P^2
= E / P
August 3rd, 2020 at 10:55:55 AM
permalink
Quote: Ace2219 rolls for a bet that has about a 1 in 6,000 chance of winning ?
Never mind, I misunderstood the question. My answer would be appropriate for this question:
Assuming the shooter could never seven-out, how many rolls on average would it take to achieve the Fire Bet?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
August 3rd, 2020 at 12:26:49 PM
permalink
CorrectQuote: ThatDonGuy
Somewhere around 52,477; it's the expected number of rolls to resolve a fire bet divided by the probability of winning
Let E be the number needed for the current shooter to win or lose the Fire Bet, and P the probability of a shooter winning the Fire Bet
First shooter wins: EP
Second shooter wins: (1-P) P x 2E
Third shooter wins: (1-P)^2 P x 3E
...
Sum = EP (1 + 2 (1-P) + 3 (1-P)^2 + ...)
= EP (1 + (1-P) + (1-P)^2 + ...)^2
= EP / P^2
= E / P
It will take an average of 1/P trials to win and each trial will average E rolls. So E/P
Can also be expressed as (1/P - 1)L where L is average rolls per shooter
It’s all about making that GTA
August 3rd, 2020 at 7:43:18 PM
permalink
Anyone here can help to solve d2y/dx2 = 1/(1-y) ?
Can I solve it this way ?
(1-y) d2y = dx2
(y - y^2/2 + c1)dy = (x + c2)dx
y^2/2 - y^3/6 + c1(y) + c3 = (x^2/2) + c2(x) + c4
Correct ?
Can I solve it this way ?
(1-y) d2y = dx2
(y - y^2/2 + c1)dy = (x + c2)dx
y^2/2 - y^3/6 + c1(y) + c3 = (x^2/2) + c2(x) + c4
Correct ?
Last edited by: ssho88 on Aug 3, 2020
August 3rd, 2020 at 8:09:05 PM
permalink
Quote: ssho88Anyone here can help to solve d2y/dx2 = 1/(1-y) ?
I cannot solve it, but at www.WolframAlpha.com, you can type in y''=1/(1-y) to get the general solution.
August 3rd, 2020 at 8:10:06 PM
permalink
Quote: ChesterDogI cannot solve it, but at www.WolframAlpha.com, you can type in y''=1/(1-y) to get the general solution.
Can I solve it this way ?
(1-y) d2y = dx2
(y - y^2/2 + c1)dy = (x + c2)dx
y^2/2 - y^3/6 + c1(y) + c3 = (x^2/2) + c2(x) + c4
Correct ?
August 3rd, 2020 at 8:35:51 PM
permalink
Quote: ssho88Quote: ChesterDogI cannot solve it, but at www.WolframAlpha.com, you can type in y''=1/(1-y) to get the general solution.
Can I solve it this way ?
(1-y) d2y = dx2
(y - y^2/2 + c1)dy = (x + c2)dx
y^2/2 - y^3/6 + c1(y) + c3 = (x^2/2) + c2(x) + c4
Correct ?
I have seen separation of variables for first degree differential equations but I haven't seen that trick for second degree equations.
Your original equation is: d2y/dx2 = 1 / (1-y).
The meaning of this is: d[dy/dx] / dx = 1 / (1-y), which can be rearranged to: (1-y)d[dy/dx] = dx. I can integrate the right to get x + c1, but I can't integrate the left because I don't know an expression for y in terms of dy/dx.
August 3rd, 2020 at 8:44:07 PM
permalink
Quote: ChesterDogQuote: ssho88Quote: ChesterDogI cannot solve it, but at www.WolframAlpha.com, you can type in y''=1/(1-y) to get the general solution.
Can I solve it this way ?
(1-y) d2y = dx2
(y - y^2/2 + c1)dy = (x + c2)dx
y^2/2 - y^3/6 + c1(y) + c3 = (x^2/2) + c2(x) + c4
Correct ?
I have seen separation of variables for first degree differential equations but I haven't seen that trick for second degree equations.
Your original equation is: d2y/dx2 = 1 / (1-y).
The meaning of this is: d[dy/dx] / dx = 1 / (1-y), which can be rearranged to: (1-y)d[dy/dx] = dx. I can integrate the right to get x + c1, but I can't integrate the left because I don't know an expression for y in terms of dy/dx.
Agree, I don't think it can be solved that way. Thanks
August 4th, 2020 at 8:00:24 AM
permalink
The Babylonians used a base 60 number system.
What shape inspired them to decide that a circle has 360 degrees?
Have you tried 22 tonight? I said 22.
August 4th, 2020 at 8:35:31 AM
permalink
Yikes, that means I would not only need to take my shoes off, but also to find 2 other barefoot friends just to count to 10! ;)Quote: Gialmere
The Babylonians used a base 60 number system.
Quote:What shape inspired them to decide that a circle has 360 degrees?
A hexagon, perhaps?
"Dealer has 'rock'... Pay 'paper!'"
August 4th, 2020 at 1:42:41 PM
permalink
Quote: JoemanA hexagon, perhaps?
Correct!
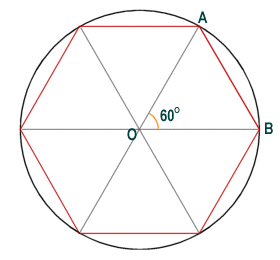
Since the perimeter of a hexagon is exactly equal to six times the radius of the circumscribed circle, they chose to divide the circle into 6 x 60 = 360 degrees.
I should note there are other reasons for the 360 degrees. What they are and why the number 360 is special makes for some interesting reading if you're bored sometime.
------------------------------------
Things I learned in organic chemistry...
1. How to draw hexagons.
Have you tried 22 tonight? I said 22.
August 4th, 2020 at 1:46:24 PM
permalink
Quote: ssho88Quote: ChesterDogI cannot solve it, but at www.WolframAlpha.com, you can type in y''=1/(1-y) to get the general solution.
Can I solve it this way ?
(1-y) d2y = dx2
(y - y^2/2 + c1)dy = (x + c2)dx
y^2/2 - y^3/6 + c1(y) + c3 = (x^2/2) + c2(x) + c4
Correct ?
edit: Chesterdog appears to have beat me to this.
I am rusty on my calculus. But I question whether you can integrate one side of an equation over x and integrate the other side of the equation over y and still have an equality. Does anyone know for sure?
Basically this is y(x) such that d2y(x)/dx2 = 1/(1-y(x)). Can you expand 1/(1-y(x)) into an infinite series and then integrate it with respect to x?
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
August 5th, 2020 at 6:05:42 PM
permalink
Two craps players make a side bet on a side bet.
Player A always plays "All Small" and "All Tall". Player B always plays "Make em All".
Starting with a new shooter, A tells B he will win both of his wagers at least twice before B wins his once. In this casino, All Small, All Tall, and Make em All bets can only be made before a new shooter's first roll.
This is an even money bet. They will play until their wager is resolved. What is A's edge (or disadvantage)?
Player A always plays "All Small" and "All Tall". Player B always plays "Make em All".
Starting with a new shooter, A tells B he will win both of his wagers at least twice before B wins his once. In this casino, All Small, All Tall, and Make em All bets can only be made before a new shooter's first roll.
This is an even money bet. They will play until their wager is resolved. What is A's edge (or disadvantage)?
It’s all about making that GTA
August 9th, 2020 at 7:30:41 AM
permalink
Quote: Ace2Two craps players make a side bet on a side bet.
Player A always plays "All Small" and "All Tall". Player B always plays "Make em All".
Starting with a new shooter, A tells B he will win both of his wagers at least twice before B wins his once. In this casino, All Small, All Tall, and Make em All bets can only be made before a new shooter's first roll.
This is an even money bet. They will play until their wager is resolved. What is A's edge (or disadvantage)?
Is there an "easy" solution to this?
I can see this as a Markov chain, but the number of states makes it really hard to solve.
The way I see it, each state consists of a Small Bet state, a Tall state, and an All state.
There are 63 Small states, ranging from 0 to 62: (31 x the number of Small bets won, up to 2) + (16 if 2 has been rolled in the current Small bet) + (8 if 3 has been rolled) + (4 if 4 has been rolled) + (2 if 5 has been rolled) + (1 if 6 has been rolled)
There are also 63 Tall states, replacing 2-6 with 8-12
There are 1024 All states: (512 if 2 has been rolled) + (256 if 3 has been rolled) + ... + (2 if 11 has been rolled) + (1 if 12 has been rolled)
This is over 4 million states, although some are not possible (for example, if there have not been any Small or Tall bets won yet, then each All state has exactly one Small/Tall state pair.)
There is the further complication that, when the Small or Tall bet is won for the first time, it does not "reset" until there is a new shooter.
August 9th, 2020 at 10:07:01 AM
permalink
There are just three relevant possibilities for every shooter: wins small, tall or all. Then there are only four states in terms of small and tall: 1 win, 2 distinct wins, 2 similar wins and 3 wins. You should be able to solve with linear equations
I solved it using calculus which, in my opinion, is much easier than linear equations.
Or my logic/math is wrong.
I solved it using calculus which, in my opinion, is much easier than linear equations.
Or my logic/math is wrong.
Last edited by: Ace2 on Aug 9, 2020
It’s all about making that GTA
August 9th, 2020 at 3:42:58 PM
permalink
/pic5539872.png)
A surveyor wants to approximate the width of a lake. He places 5 markers near the lake and measures the distances shown in the diagram above.
What is the width of the lake in meters from point P to point Q?
Have you tried 22 tonight? I said 22.
August 9th, 2020 at 4:11:21 PM
permalink
200 m
It’s all about making that GTA
August 9th, 2020 at 4:36:56 PM
permalink
My answer is 200 m ***
***: I got 200.00000000002351265624999861789 on the calculator
Note: I used variations of "a2 + b2 = c2" and the "Cosine Rule" to work this out (I forgot how to do it, so had to look up when to use cos and cos-1 on the calculator).
***: I got 200.00000000002351265624999861789 on the calculator
Note: I used variations of "a2 + b2 = c2" and the "Cosine Rule" to work this out (I forgot how to do it, so had to look up when to use cos and cos-1 on the calculator).
August 9th, 2020 at 5:58:07 PM
permalink
I tried to use similar triangles theorem to compare the bases of the smaller triangle and the larger triangle to the area. I thought they should be in the same proportion? I got 150m, but I'm guessing I've done something wrong. Can anyone enlighten me?
ETA: I figured it out.. the areas aren't proportional. But the sides are so I essentially did x/(100+x) = 100/150. Giving x=200
ETA: I figured it out.. the areas aren't proportional. But the sides are so I essentially did x/(100+x) = 100/150. Giving x=200
August 9th, 2020 at 6:13:13 PM
permalink
Similar triangles does work (I'm assuming the line across the lake is NS and the others EW).
The base of the big triangle is 150m, and the base of the smaller triangle is 100m.
If the height of the smaller triangle is x (i.e. the distance across the lake), then the height of the larger triangle is 150/100*x = 1.5x.
We're told the difference in heights is 100m;so (1.5x - x)=100m; so x=200m.
If the height of the smaller triangle is x (i.e. the distance across the lake), then the height of the larger triangle is 150/100*x = 1.5x.
We're told the difference in heights is 100m;so (1.5x - x)=100m; so x=200m.
August 9th, 2020 at 8:30:03 PM
permalink
Deleted
It’s all about making that GTA
August 9th, 2020 at 11:27:05 PM
permalink
Quote: Ace2200 m
Quote: ksdjdjMy answer is 200 m ***
***: I got 200.00000000002351265624999861789 on the calculator
Note: I used variations of "a2 + b2 = c2" and the "Cosine Rule" to work this out (I forgot how to do it, so had to look up when to use cos and cos-1 on the calculator).
Quote: rsactuaryI tried to use similar triangles theorem to compare the bases of the smaller triangle and the larger triangle to the area. I thought they should be in the same proportion? I got 150m, but I'm guessing I've done something wrong. Can anyone enlighten me?
ETA: I figured it out.. the areas aren't proportional. But the sides are so I essentially did x/(100+x) = 100/150. Giving x=200
Quote: charliepatrickSimilar triangles does work (I'm assuming the line across the lake is NS and the others EW).
The base of the big triangle is 150m, and the base of the smaller triangle is 100m.
If the height of the smaller triangle is x (i.e. the distance across the lake), then the height of the larger triangle is 150/100*x = 1.5x.
We're told the difference in heights is 100m;so (1.5x - x)=100m; so x=200m.
Correct!
---------------------------
My dad taught me how to swim by throwing me into a lake.
The swimming part was easy but getting out of the burlap sack took some work.
Have you tried 22 tonight? I said 22.
August 10th, 2020 at 9:14:48 AM
permalink
If anyone cares:Quote: Ace2Two craps players make a side bet on a side bet.
Player A always plays "All Small" and "All Tall". Player B always plays "Make em All".
Starting with a new shooter, A tells B he will win both of his wagers at least twice before B wins his once. In this casino, All Small, All Tall, and Make em All bets can only be made before a new shooter's first roll.
This is an even money bet. They will play until their wager is resolved. What is A's edge (or disadvantage)?
The overall probability x of winning the Small bet is 0.026354 and the overall probability y of winning the All bet is 0.005258. However, if the only three relevant outcomes are winning Small, Tall or All then the probability s of winning only the Small bet is (x-y)/(2x-y) = 0.44459. If we consider only two outcomes of winning Small or All then the probability m of winning Small (only) is (x-y)/x = 0.80049
Using linear equations where state a is 1 small or tall win, state b is 2 similar wins, state c is 2 distinct wins and state d is 3 wins we can say:
x = 2sa
a = s(b + c)
b = md
c = 2sd
d = m
Solve for x and the probability of player A winning is 0.5347 for a 6.94% advantage
However, it’s easier to solve this by integrating the following equation from zero to infinity:
(e^(sx) - sx - 1) * sx/e^x * 2s
It’s all about making that GTA
August 10th, 2020 at 9:32:37 AM
permalink
Quote: Ace2If anyone cares:
The overall probability x of winning the Small bet is 0.026354 and the overall probability y of winning the All bet is 0.005258. However, if the only three relevant outcomes are winning Small, Tall or All then the probability s of winning only the Small bet is (x-y)/(2x-y) = 0.44459. If we consider only two outcomes of winning Small or All then the probability m of winning Small (only) is (x-y)/x = 0.80049
Using linear equations where state a is 1 small or tall win, state b is 2 similar wins, state c is 2 distinct wins and state d is 3 wins we can say:
x = 2sa
a = s(b + c)
b = md
c = 2sd
d = m
Solve for x and the probability of player A winning is 0.5347 for a 6.94% advantage
However, it’s easier to solve this by integrating the following equation from zero to infinity:
(e^(sx) - sx - 1) * sx/e^x * 2s
I’m not quite following. How did you derive the conditional probability of hitting the All given that the Small has just been hit?
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
August 10th, 2020 at 10:14:44 AM
permalink
I didn’t. There are only 3 relevant outcomes:Quote: unJonI’m not quite following. How did you derive the conditional probability of hitting the All given that the Small has just been hit?
Shooter wins small (only)
Shooter wins tall (only)
Shooter wins all
It’s all about making that GTA
August 10th, 2020 at 10:32:24 AM
permalink
Quote: Ace2I didn’t. There are only 3 relevant outcomes:
Shooter wins small (only)
Shooter wins tall (only)
Shooter wins all
Oh I see. You actually implicitly have it: 1 - (x - y) / x.
How about this one: what’s the expected number of rolls for this bet between A and B to resolve?
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
