Poll
| No votes (0%) | |||
| No votes (0%) | |||
 | 2 votes (66.66%) | ||
| No votes (0%) | |||
 | 1 vote (33.33%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
 | 1 vote (33.33%) | ||
 | 3 votes (100%) | ||
| No votes (0%) |
3 members have voted
March 16th, 2020 at 6:48:42 AM
permalink
I know this one is very similar to the Cone Mountain puzzle, but that one was difficult to word. Hopefully this one will be more clear.
There is a teepee with radius 3 meters and height 5 meters. You wish to stake a rope to anywhere on the base of the teepee, wrap it entirely around the teepee once somehow, and tie the other end to the stake where you started.
1. What is the minimum length of rope needed?
2. Assuming the minimum length is used, what is the closest the rope gets to the tip of the teepee?

Photo credit: Wikipedia
There is a teepee with radius 3 meters and height 5 meters. You wish to stake a rope to anywhere on the base of the teepee, wrap it entirely around the teepee once somehow, and tie the other end to the stake where you started.
1. What is the minimum length of rope needed?
2. Assuming the minimum length is used, what is the closest the rope gets to the tip of the teepee?

Photo credit: Wikipedia
- Please don't just plop a URL to a solution elsewhere until a winner here has been declared.
- All those who have won a beer previously are asked to not post answers or solutions for 24 after this posting. Past winners who must chime in early, may PM me.
- Beer to the first satisfactory answer and solution, subject to rule 2.
- Please put answers and solutions in spoiler tags.
Last edited by: Wizard on Mar 17, 2020
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 16th, 2020 at 8:46:47 AM
permalink
If slant height = 5m, minimum length of rope needed= (50*(1- cos(216 degree)))^0.5 = 9.5106m, minimum distance between rope and the tip = 0.5 * (100-50*(1- cos(216 degree))^0.5 = 1.5451m
Last edited by: ssho88 on Mar 16, 2020
March 16th, 2020 at 10:17:44 AM
permalink
I have been hoarding teepees.
Sorry, wrong thread
Sorry, wrong thread
March 16th, 2020 at 10:32:49 AM
permalink
Five meters is NOT the slant height, it's the height from the center of the base to the tip.
I redid the numbers to not need to mention the slant height, fearing many people may not know what that is.
I redid the numbers to not need to mention the slant height, fearing many people may not know what that is.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 16th, 2020 at 11:08:57 AM
permalink
Either the answer is 6pi or you mean the rope wraps up the teepee, reaching the peak, then drops to the starting point.
In that case, wouldn't we need to know the thickness of the rope?
In that case, wouldn't we need to know the thickness of the rope?
I invented a few casino games. Info:
http://www.DaveMillerGaming.com/ —————————————————————————————————————
Superstitions are silly, irrational, childish rituals, born out of fear of the unknown. But how much does it cost to knock on wood? 😁
March 16th, 2020 at 12:22:56 PM
permalink
Quote: DJTeddyBearEither the answer is 6pi or you mean the rope wraps up the teepee, reaching the peak, then drops to the starting point.
There is a better answer in between those two extremes.
Quote:In that case, wouldn't we need to know the thickness of the rope?
Just assume it's string. We don't need to muddy the water with rope thickness.
Last edited by: Wizard on Mar 31, 2020
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 16th, 2020 at 4:06:36 PM
permalink
Minimum length of rope = 11.6498m and it is 0.26545m away from the tip. I think DJTeddyBear should be the winner !
By the way, I think the teepee is stable and can withstand strong wind.
By the way, I think the teepee is stable and can withstand strong wind.
Last edited by: ssho88 on Mar 16, 2020
March 16th, 2020 at 4:50:03 PM
permalink
Whoa....Quote: WizardJust assuming it's string. We don't need to muddy the water with rope thickness.
I just did a quick Google search for ‘rope’. The first two links were images of rope for sale. It came in size from 1/4” to 1”.
A similar Google search for ‘string’ and also had links to purchase it, but only one of them had a size. 1/8“.
Obviously a 1/8” string is gonna take 8 times the length to get the same lateral height as a 1” rope.
So my answer remains that there’s insufficient information.
I invented a few casino games. Info:
http://www.DaveMillerGaming.com/ —————————————————————————————————————
Superstitions are silly, irrational, childish rituals, born out of fear of the unknown. But how much does it cost to knock on wood? 😁
March 16th, 2020 at 7:48:49 PM
permalink
Quote: ssho88Minimum length of rope = 11.6498m and it is 0.26545m away from the tip. I think DJTeddyBear should be the winner !
By the way, I think the teepee is stable and can withstand strong wind.
Congratulations! This is the correct answer. I put the dimensions of the teepee incorrectly, but your answer is right for what I asked.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 16th, 2020 at 8:13:26 PM
permalink
I hate to belabor this problem, but what would the answers be if the radius of the teepee were 5 meters and the slant height (distance from edge of base to tip) was 20 meters?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 17th, 2020 at 7:02:11 AM
permalink
OH! Now that I see other replies, I realize what this question is really asking:
With a cone of this size, what's the smallest circumference an ellipse can have where one edge is at the base of the cone?
For the record, I believe that would be an ellipse where it's angle of inclination is at right angles to the opposite side from where it touches the base.
That in mind, I have no idea how to calculate such an ellipse, I'm just happy I figured out what is really being asked — and how to properly phrase it. 😁
And for the record, I REALLY thought that the rope was supposed to continuously wrap up the outside of the teepee, so that viewed from above it looks like a spiral. Viewed from the side, I thought it kinda looks like this:
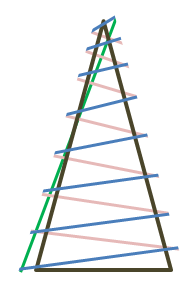
Now I hope you realize why I thought that the size of the rope was important. 🤪
With a cone of this size, what's the smallest circumference an ellipse can have where one edge is at the base of the cone?
For the record, I believe that would be an ellipse where it's angle of inclination is at right angles to the opposite side from where it touches the base.
That in mind, I have no idea how to calculate such an ellipse, I'm just happy I figured out what is really being asked — and how to properly phrase it. 😁
And for the record, I REALLY thought that the rope was supposed to continuously wrap up the outside of the teepee, so that viewed from above it looks like a spiral. Viewed from the side, I thought it kinda looks like this:

Now I hope you realize why I thought that the size of the rope was important. 🤪
I invented a few casino games. Info:
http://www.DaveMillerGaming.com/ —————————————————————————————————————
Superstitions are silly, irrational, childish rituals, born out of fear of the unknown. But how much does it cost to knock on wood? 😁
March 17th, 2020 at 7:28:51 AM
permalink
Quote: DJTeddyBearWith a cone of this size, what's the smallest circumference an ellipse can have where one edge is at the base of the cone?
Yes, the rope wraps around just ONCE. You are correct that it will form an ellipse.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 17th, 2020 at 8:16:23 AM
permalink
Quote: WizardI hate to belabor this problem, but what would the answers be if the radius of the teepee were 5 meters and the slant height (distance from edge of base to tip) was 20 meters?
I think this forms a right angle triangle as the radius is 20 and the arc length 10 Pi (2 Pi R) so the angle is Pi/2 = 90 degrees. Thus the answer would be 20 SQRT(2).
btw I didn't understand the other puzzle as I got R = SQRT(34) = 5.8309 and the arc as 6 Pi. So the angle exceeded 180o which meant the shortest was a virtual route rather than one which would lie on the surface. Perhaps I've misunderstood something...
btw I didn't understand the other puzzle as I got R = SQRT(34) = 5.8309 and the arc as 6 Pi. So the angle exceeded 180o which meant the shortest was a virtual route rather than one which would lie on the surface. Perhaps I've misunderstood something...
March 17th, 2020 at 7:49:16 PM
permalink
Quote: charliepatrickI think this forms a right angle triangle as the radius is 20 and the arc length 10 Pi (2 Pi R) so the angle is Pi/2 = 90 degrees. Thus the answer would be 20 SQRT(2).
Thanks, I agree. I'll reply by PM to your second point.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)


