Poll
| No votes (0%) | |||
| No votes (0%) | |||
 | 2 votes (50%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
 | 1 vote (25%) | ||
 | 3 votes (75%) | ||
 | 2 votes (50%) | ||
 | 3 votes (75%) | ||
 | 1 vote (25%) |
4 members have voted
Cone Mountain is in the shape of a cone. The radius is 2 kilometers and the slant height is 6 kilometers. There is a road that ends at an observation point half way up the mountain. The observation point is directly half way between the start of the road and the summit. The road takes the shortest possible route while also making a complete revolution around the mountain.
Question 1: What is the full length of the road?
Question 2: What length of the road goes downhill (if going to the observation point)?
Beer to the first satisfactory answer and solution to question 2, subject to the usual rules:
- Please don't just plop a URL to a solution elsewhere until a winner here has been declared.
- All those who have won a beer previously are asked to not post answers or solutions for 24 after this posting. Past winners who must chime in early, may PM me.
- Beer to the first satisfactory answer and solution, subject to rule 2.
- Please put answers and solutions in spoiler tags.
Edit: and what’s the difference between the road and the trail?
Quote: unJonDoes the road make one revolution between the bottom of the mountain and (x) the observation point or (y) the summit?
The observation point. The road ends there.
Quote:Edit: and what’s the difference between the road and the trail?
Sorry, where I said "trail" I should have said "road."
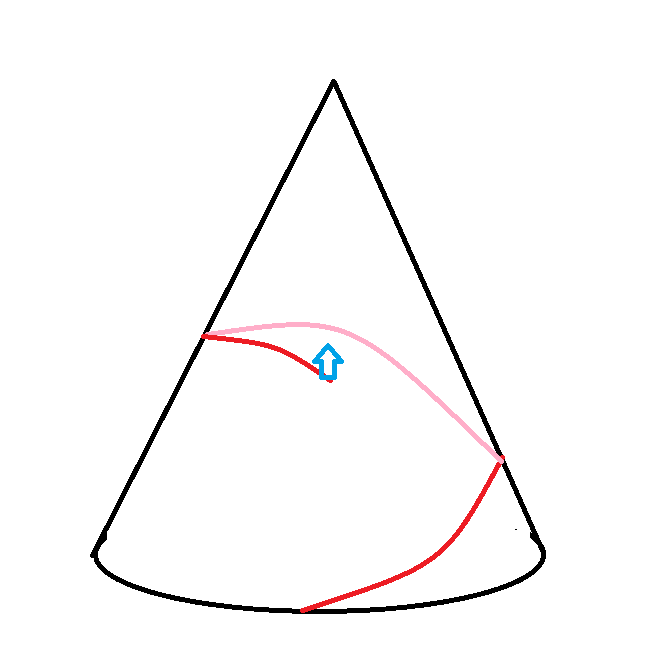
The blue arrow represents the bathroom at the observation platform. The pink part of the road is behind the mountain.
Forgive the awful graphic, but I hope it represents the goal is the observation platform. The road does not go to the summit on the way and it makes one revolution only around the mountain.
I also realize that saying the path is "straight" may lead to some confusion, as the math is clearly on a curved cone. How shall I put it? I think this would be correct -- the path can be any shape that gets to the observation point and makes a complete revolution around the mountain.
Quote: WizardI got a response from a "beer club" member that makes me think I haven't stated the question clearly.
The blue arrow represents the bathroom at the observation platform. The pink part of the road is behind the mountain.
Forgive the awful graphic, but I hope it represents the goal is the observation platform. The road does not go to the summit on the way and it makes one revolution only around the mountain.
I also realize that saying the path is "straight" may lead to some confusion, as the math is clearly on a curved cone. How shall I put it? I think this would be correct -- the path can be any shape that gets to the observation point and makes a complete revolution around the mountain.
Quite hard, is it necessary/possible to define the path into an math equations ? I guess it is about distance in 3 dimensional.
Quote: ssho88Quite hard, is it necessary/possible to define the path into an math equations ? I guess it is about distance in 3 dimensional.
I'd like to not give hints until after the the 24-hour Beer Club waiting period is over. I will say I was able to do the problem. The way I did it is not that complicated, but it may not be obvious to solve it the way I did.
I guess the shortest path should be :-
a) Go straight to the observation point, Distance A = 3, slant height !
b) Then turn one round horizontally, Distance B = 2*PI, Edited should be 2 * PI !
Total shortest distance = 2*PI + 3 = 9.2832km
Is it correct ? LOL
I'm not sure I agree with your figures...Quote: ssho88
I guess the shortest path should be :-
a) Go straight to the observation point, Distance A = 10^0.5
b) Then turn one round horizontally, Distance B = PI
Total shortest distance = PI + 10^0.5
Is it correct ? LOL
Then walking horizontally around the circle, it now has a radius of 1, so is 2 Pi. This gives a total of about 9.14 Km.
Surely as you approach the observation point, say 50m before you get there it is better to head off to one side to join the horizontal path - i.e go along one side of the triangle rather than two.
Quote: ssho88
I guess the shortest path should be :-
a) Go straight to the observation point, Distance A = 10^0.5
b) Then turn one round horizontally, Distance B = PI
Total shortest distance = PI + 10^0.5
Is it correct ? LOL
I don't think so - instead of a cone, use a cylinder with radius 1 where the point is distance D from the start:
The "straight up and then around" method would be D + 2 PI = sqrt(D2 + (2 PI)2 + 4 PI D)
However, if you roll the surface out to a rectangle, the shortest distance is sqrt(D2 + (2 PI)2)
Then again, I assumed the cone solution would be similar, and the "downhill distance" would be zero.
Quote: rdw4potusAny answer >9km is wrong, else you could walk to the summit, twirl around the peak, and walk back to the observation post.
This is a good insight.
Quote: unJonThis is a good insight.
deleted
Quote: charliepatrickI'm not sure I agree with your figures...Quote: ssho88
I guess the shortest path should be :-
a) Go straight to the observation point, Distance A = 10^0.5
b) Then turn one round horizontally, Distance B = PI
Total shortest distance = PI + 10^0.5
Is it correct ? LOLWalking directly up to the observation point is surely along half the side, so is 6/2 = 3Km.
Then walking horizontally around the circle, it now has a radius of 1, so is 2 Pi. This gives a total of about 9.14 Km.
Surely as you approach the observation point, say 50m before you get there it is better to head off to one side to join the horizontal path - i.e go along one side of the triangle rather than two.
You are correct, 6km is slant height ! I assumed it is vertical height in early reply.
Quote: rdw4potusAny answer >9km is wrong, else you could walk to the summit, twirl around the peak, and walk back to the observation post.
...that this is the correct answer - the road goes up to the summit, then around it, then back down, so it would be a total of 9 km, of which 3 km is downhill?
Flatten the mountain onto a plane; it is a circle. There is a starting point, a point representing the summit, and a point representing the ending point, which is the midpoint of the line segment from the start to the summit. The path must go around the summit. It seems that the shortest distance is to go straight to the summit, go around it with a small a radius as possible, then return by a straight line to the end of the road.
The reason I question this is, it would be the same regardless of the radius of the cone's base, which doesn't seem intuitive.
Quote: ThatDonGuy
...that this is the correct answer - the road goes up to the summit, then around it, then back down, so it would be a total of 9 km, of which 3 km is downhill?
Flatten the mountain onto a plane; it is a circle. There is a starting point, a point representing the summit, and a point representing the ending point, which is the midpoint of the line segment from the start to the summit. The path must go around the summit. It seems that the shortest distance is to go straight to the summit, go around it with a small a radius as possible, then return by a straight line to the end of the road.
The reason I question this is, it would be the same regardless of the radius of the cone's base, which doesn't seem intuitive.
Well:
My solution is less than 8 km.
Quote: Wizard...My solution is less than 8 km.
 The trick is to consider the cone as a slice of pie, the sides/radius are 6Km (TR and TP) and the arc (PQR) is 4 Pi (this comes from the circumference of the original cone as 2 Pi R where R = 2Km).
The trick is to consider the cone as a slice of pie, the sides/radius are 6Km (TR and TP) and the arc (PQR) is 4 Pi (this comes from the circumference of the original cone as 2 Pi R where R = 2Km).As the arc is 4 Pi and the radius is 6, the angle is 2/3 Pi which is the same as 120o. Thus you could consider two equilateral triangles.
The path starts at the bottom of the hill (R) and goes to a point half way up by which time you've gone all the way round the cone. (With other values for the radius, where the angle exceeds 180 it would be correct to go via the top, but not in this case.)
Considering the triangle TRH, you could construct (red HST) half an equilateral triangle, so SH = SQRT ( 9 - 2.25 ).
Thus RH is SQRT ( RS^2 + HS^2 ) = SQRT ( 56.25 + 9 - 2.25 ) = SQRT (63).
For Part II, the line RH is nearest the top (and hence then starts to go back downhill) where it meets a radius at 90o. By similar triangles (share angle SRH) the path length is 6 * (7.5 / SQRT (63) ) = SQRT (2025/63) = 5.669.
Quote: charliepatrickSo is mine at SQRT(63).The trick is to consider the cone as a slice of pie, the sides/radius are 6Km (TR and TP) and the arc (PQR) is 4 Pi (this comes from the circumference of the original cone as 2 Pi R where R = 2Km).
As the arc is 4 Pi and the radius is 6, the angle is 2/3 Pi which is the same as 120o. Thus you could consider two equilateral triangles.
The path starts at the bottom of the hill (R) and goes to a point half way up by which time you've gone all the way round the cone. (With other values for the radius, where the angle exceeds 180 it would be correct to go via the top, but not in this case.)
Considering the triangle TRH, you could construct (red HST) half an equilateral triangle, so SH = SQRT ( 9 - 2.25 ).
Thus RH is SQRT ( RS^2 + HS^2 ) = SQRT ( 56.25 + 9 - 2.25 ) = SQRT (63).
For Part II, the line RH is nearest the top (and hence then starts to go back downhill) where it meets a radius at 90o. By similar triangles (share angle SRH) the path length is 6 * (7.5 / SQRT (63) ) = SQRT (2025/63) = 5.669.
I agree! Very nice solution too. I appreciate the graphic. Add one to the tally of beers I owe you. I will double the total if enjoyed in the wee little village of Shackleford.
It's not that far from where I live (about 1 hour) and it does have a nice sounding pub.Quote: Wizard... beers...in the wee little village of Shackleford.
Quote: charliepatrickIt's not that far from where I live (about 1 hour) and it does have a nice sounding pub.Quote: Wizard... beers...in the wee little village of Shackleford.
The food looks delicious on their Facebook page. They celebrate Mother's Day way too early, though.


