Poll
| No votes (0%) | |||
| No votes (0%) | |||
 | 2 votes (100%) | ||
| No votes (0%) | |||
 | 2 votes (100%) | ||
 | 1 vote (50%) | ||
 | 1 vote (50%) | ||
 | 2 votes (100%) | ||
| No votes (0%) | |||
 | 1 vote (50%) |
2 members have voted
March 10th, 2020 at 3:48:07 PM
permalink
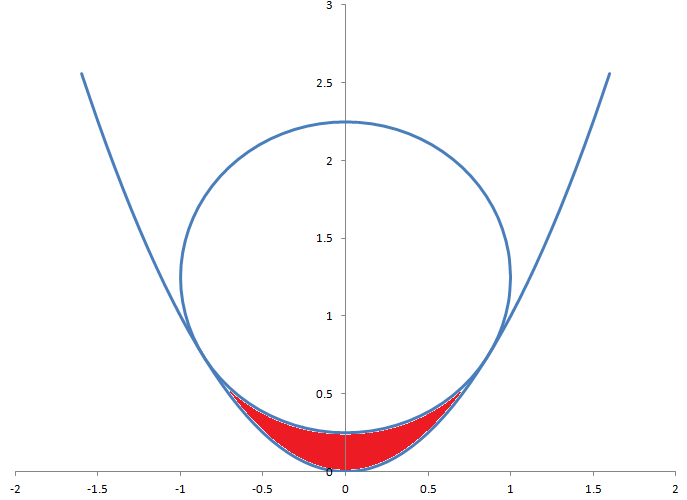
A circle of radius 1 is tangent to a parabola of equation y=x2. What is the area of the region in red, between the circle and parabola?
Usual rules:
- Please don't just plop a URL to a solution elsewhere until a winner here has been declared.
- All those who have won a beer previously are asked to not post answers or solutions for 24 after this posting. Past winners who must chime in early, may PM me.
- Beer to the first satisfactory answer and solution, subject to rule 2.
- Please put answers and solutions in spoiler tags.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 10th, 2020 at 5:27:21 PM
permalink
Area = 3*(3)^0.5/4 - PI/3 = 0.25184, I will post the calculations if the answer is correct
https://ibb.co/1GKFM66
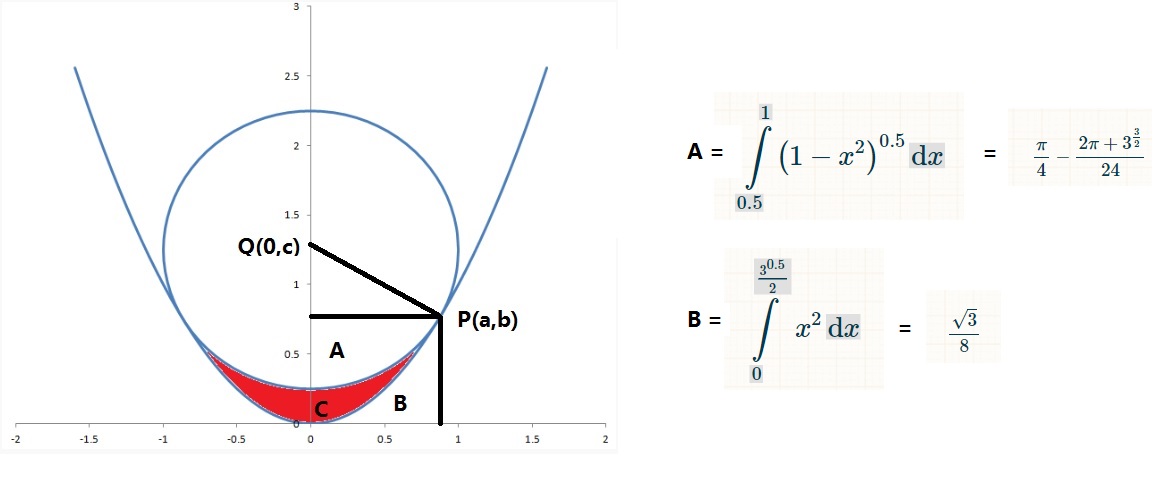
Q(0,c) is center of the circle, P(a,b) is the intersection point.
Gradient of Line PQ = m1 = (b-c)/a
Gradient of tangent to the parabolic at P(a, b) = m2 = dy/dx = 2x = 2a
So, m1 * m2 = -1
(b-c)/a * 2a = -1
c= 0.5 + b ------------- Eq1
Parabolic EQuation,
y = x^2, So, b = a^2 ---------------Eq2
Circle Equation,
x^2 + (y-c)^2 = 1
So, a^2 (b-c)^2 = 1 ---------------Eq3
From Eq1, Eq2 and Eq3,
b + (b- 0.5 - b)^2 = 1
b = 0.75 = 3/4
c = 1.25 = 5/4
a = (0.75)^0.5 = (3)^0.5/2
AREA A = PI/4 -(2*PI + 3(3)^0.5)/24
AREA B = 3(3)^0.5)/24
AREA A + AREA B = PI/4 -2*PI/24 = PI/6
RED Area = 2 * [a*b - (AREA A + AREA B)]
= 2 * [(3)^2/2 * 3/4 - PI/6]
= (3)^0.5 * 3/4 - PI/3
= 0.25184
https://ibb.co/1GKFM66
Q(0,c) is center of the circle, P(a,b) is the intersection point.
Gradient of Line PQ = m1 = (b-c)/a
Gradient of tangent to the parabolic at P(a, b) = m2 = dy/dx = 2x = 2a
So, m1 * m2 = -1
(b-c)/a * 2a = -1
c= 0.5 + b ------------- Eq1
Parabolic EQuation,
y = x^2, So, b = a^2 ---------------Eq2
Circle Equation,
x^2 + (y-c)^2 = 1
So, a^2 (b-c)^2 = 1 ---------------Eq3
From Eq1, Eq2 and Eq3,
b + (b- 0.5 - b)^2 = 1
b = 0.75 = 3/4
c = 1.25 = 5/4
a = (0.75)^0.5 = (3)^0.5/2
AREA A = PI/4 -(2*PI + 3(3)^0.5)/24
AREA B = 3(3)^0.5)/24
AREA A + AREA B = PI/4 -2*PI/24 = PI/6
RED Area = 2 * [a*b - (AREA A + AREA B)]
= 2 * [(3)^2/2 * 3/4 - PI/6]
= (3)^0.5 * 3/4 - PI/3
= 0.25184
EDITED
Last edited by: ssho88 on Mar 10, 2020
March 10th, 2020 at 6:08:19 PM
permalink
Quote: ssho88Area = 3*(3)^0.5/4 - PI/3 = 0.25184, I will post the calculations if the answer is correct
I agree this is the correct answer. For the beer, you must show your work. There is still opportunity for anyone else to swoop in before to claim it, except those already on the "beer list."
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 10th, 2020 at 7:25:55 PM
permalink
Quote: WizardQuote: ssho88Area = 3*(3)^0.5/4 - PI/3 = 0.25184, I will post the calculations if the answer is correct
I agree this is the correct answer. For the beer, you must show your work. There is still opportunity for anyone else to swoop in before to claim it, except those already on the "beer list."
https://ibb.co/1GKFM66
Q(0,c) is center of the circle, P(a,b) is the intersection point.
Gradient of Line PQ = m1 = (b-c)/a
Gradient of tangent to the parabolic at P(a, b) = m2 = dy/dx = 2x = 2a
So, m1 * m2 = -1
(b-c)/a * 2a = -1
c= 0.5 + b ------------- Eq1
Parabolic EQuation,
y = x^2, So, b = a^2 ---------------Eq2
Circle Equation,
x^2 + (y-c)^2 = 1
So, a^2 (b-c)^2 = 1 ---------------Eq3
From Eq1, Eq2 and Eq3,
b + (b- 0.5 - b)^2 = 1
b = 0.75 = 3/4
c = 1.25 = 5/4
a = (0.75)^0.5 = (3)^0.5/2
See attached image,
AREA A = PI/4 -(2*PI + 3(3)^0.5)/24
AREA B = 3(3)^0.5)/24
AREA A + AREA B = PI/4 -2*PI/24 = PI/6
RED Area = 2 * [a*b - (AREA A + AREA B)]
= 2 * [(3)^2/2 * 3/4 - PI/6]
= (3)^0.5 * 3/4 - PI/3
= 0.25184
March 10th, 2020 at 7:37:56 PM
permalink
Quote: ssho88
A bit cryptic, but I'll accept that. Well done -- I owe you a beer. Please consider yourself on the "beer list" from now on, which means you're on a 24-hour delay for future problems.
Here is your image, for all to enjoy without linking.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 11th, 2020 at 12:31:18 PM
permalink
I was thinking about solving this in a different way. Please let me know how wrong I am.
given the formula for the circle that you can find from ssho88's work, what I was thinking of would be to calculate the area under the curve of the circle between 0 and b,
subtract the area under the curve of the parabola between a and b,
and double it.
given the formula for the circle that you can find from ssho88's work, what I was thinking of would be to calculate the area under the curve of the circle between 0 and b,
subtract the area under the curve of the parabola between a and b,
and double it.
March 11th, 2020 at 2:01:50 PM
permalink
Quote: Dalex64I was thinking about solving this in a different way. Please let me know how wrong I am.
given the formula for the circle that you can find from ssho88's work, what I was thinking of would be to calculate the area under the curve of the circle between 0 and b,
subtract the area under the curve of the parabola between a and b,
and double it.
That would work. It still leaves the hard part of the problem, finding the point where the circle and parabola are tangent and finding the area under the circle for that portion.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 11th, 2020 at 4:37:24 PM
permalink
I get the same answer, but in a slightly different method from everybody else, although the first part appears to be the same as ssho88's method (and, to be honest, I had to look up one of the integrals, so even had I entered on time, it would have been with an asterisk):
Let (0,c) be the center of the circle, and (t, t2) the point of tangency with x > 0
At (t, t2), the tangent to the parabola has slope 2t, so the perpendicular to the tangent has slope -1/(2t)
This means the line containing the center of the circle and the tangent point is y = -1/2t x + c
Since (t, t2) is on this line, t2 = -1/(2t) * t + c = c - 1/2 -> c = t2 + 1/2
Since the circle has radius 1, (t - 0)2 + (t2 - c)2 = 12 = 1
Substitute t2 + 1/2 for c: t2 + (t2 - (t2 + 1/2))2 = 1
t2 + (1/2)2 = 1 -> t2 = 3/4 -> c = 5/4 and t = sqrt(3)/2
The red area = the area underneath the circle between the tangent points - the area underneath the parabola between the tangent points
Since the graphs are symmetrical with respect to the y-axis, this = 2 * (the area underneath the circle - the area underneath the parabola) for 0 <= x <= sqrt(3)/2
The graph of the bottom semicircle of the circle is y = 5/4 - sqrt(1 - x2)
This = 2 INTEGRAL(0, sqrt(3) / 2) {5/4 - sqrt(1 - x2) - x2) dx}
= 2 (INTEGRAL(0, sqrt(3) / 2) {5/4 dx} - INTEGRAL(0, sqrt(3) / 2) {sqrt(1 - x2) dx} - INTEGRAL(0, sqrt(3) / 2) {x2 dx})
The one in the middle is the one I had to look up; go down to #8
Area = 2 (5/4 * sqrt(3) / 2 - sqrt(3)/4 sqrt(1 - 3/4) + 1/2 arcsin (sqrt(3)/2) - (sqrt(3)/2)3 / 3)
= 2 (5/8 sqrt(3) - 1/8 sqrt(3) - 1/2 * PI/3 - 1/8 sqrt(3))
= 2 (3/8 sqrt(3) - PI/6)
= 3/4 sqrt(3) - PI/3
Let (0,c) be the center of the circle, and (t, t2) the point of tangency with x > 0
At (t, t2), the tangent to the parabola has slope 2t, so the perpendicular to the tangent has slope -1/(2t)
This means the line containing the center of the circle and the tangent point is y = -1/2t x + c
Since (t, t2) is on this line, t2 = -1/(2t) * t + c = c - 1/2 -> c = t2 + 1/2
Since the circle has radius 1, (t - 0)2 + (t2 - c)2 = 12 = 1
Substitute t2 + 1/2 for c: t2 + (t2 - (t2 + 1/2))2 = 1
t2 + (1/2)2 = 1 -> t2 = 3/4 -> c = 5/4 and t = sqrt(3)/2
The red area = the area underneath the circle between the tangent points - the area underneath the parabola between the tangent points
Since the graphs are symmetrical with respect to the y-axis, this = 2 * (the area underneath the circle - the area underneath the parabola) for 0 <= x <= sqrt(3)/2
The graph of the bottom semicircle of the circle is y = 5/4 - sqrt(1 - x2)
This = 2 INTEGRAL(0, sqrt(3) / 2) {5/4 - sqrt(1 - x2) - x2) dx}
= 2 (INTEGRAL(0, sqrt(3) / 2) {5/4 dx} - INTEGRAL(0, sqrt(3) / 2) {sqrt(1 - x2) dx} - INTEGRAL(0, sqrt(3) / 2) {x2 dx})
The one in the middle is the one I had to look up; go down to #8
Area = 2 (5/4 * sqrt(3) / 2 - sqrt(3)/4 sqrt(1 - 3/4) + 1/2 arcsin (sqrt(3)/2) - (sqrt(3)/2)3 / 3)
= 2 (5/8 sqrt(3) - 1/8 sqrt(3) - 1/2 * PI/3 - 1/8 sqrt(3))
= 2 (3/8 sqrt(3) - PI/6)
= 3/4 sqrt(3) - PI/3
March 12th, 2020 at 7:34:48 PM
permalink
Here is my solution in PDF form.
Yay math! (version 2)
Yay math! (version 2)
Last edited by: Wizard on Mar 13, 2020
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 13th, 2020 at 11:56:33 AM
permalink
Just curious -- why do you have the coordinates of some points in your figures shown as (x,y) (as for the point of tangency) and others shown as (y,x) (as for the center of the circle and for the point on the y axis even with the point of tangency)?Quote: WizardHere is my solution in PDF form.
March 13th, 2020 at 2:36:32 PM
permalink
Quote: DocJust curious -- why do you have the coordinates of some points in your figures shown as (x,y) (as for the point of tangency) and others shown as (y,x) (as for the center of the circle and for the point on the y axis even with the point of tangency)?
You're absolutely right. I just fixed it. Please check the previous link again.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 13th, 2020 at 6:20:10 PM
permalink
Mike, I know I am just being petty/nerdy here ....Quote: WizardI just fixed it.
In the text between the two figures that you edited, there are two lines referring to (a,0) and (b2,0). You are generally quite precise, so I didn't think you would want it to stand that way.


