Poll
 | 1 vote (14.28%) | ||
 | 1 vote (14.28%) | ||
 | 2 votes (28.57%) | ||
| No votes (0%) | |||
| No votes (0%) | |||
 | 3 votes (42.85%) | ||
 | 3 votes (42.85%) | ||
 | 2 votes (28.57%) | ||
 | 1 vote (14.28%) | ||
 | 4 votes (57.14%) |
7 members have voted
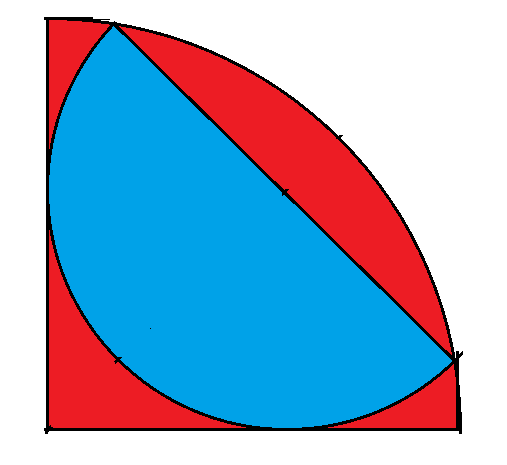
What is the ratio of the area of the semi-circle to the quarter-circle?
As usual, no searching and put answers/solutions in spoiler tags.
My thanks to Dalex64 for this problem.
p.s. Looks like I'll be spending New Years Eve at home, as usual. If you have any good math problems to help me kill the time until midnight, please PM me.
Quote: Wizardp.s. Looks like I'll be spending New Years Eve at home, as usual. If you have any good math problems to help me kill the time until midnight, please PM me.
One of my favorites ... without using a calculator, which is larger, pi^e or e^pi ?
Quote: teliotOne of my favorites ... without using a calculator, which is larger, pi^e or e^pi ?
I was messing around with Taylor expansions, which lead nowhere. Eventually, I cheated and looked up the answer. What is my punishment?
As punishment, you must do the dance in this video:Quote: WizardI was messing around with Taylor expansions, which lead nowhere. Eventually, I cheated and looked up the answer. What is my punishment?
Quote: teliotAs punishment, you must do the dance in this video:
Can I take door #2? Even compared to most white males, I'm an awful dancer.
BTW, I'm still waiting on an answer to the original problem.
Door #2. Take out your phone and ask Google Assistant (or Siri) to count backwards from 100.Quote: WizardCan I take door #2? Even compared to most white males, I'm an awful dancer.
BTW, I'm still waiting on an answer to the original problem.
I've seen many puzzles like this one over the years ... they were never that interesting to me.
If you want to pass some quality time with some truly fascinating math, there is a brilliant YouTube series on big numbers I'd suggest.
Quote: WizardA semi-circle is inscribed in a quarter-circle as follows:
What is the ratio of the area of the semi-circle to the quarter-circle?
As usual, no searching and put answers/solutions in spoiler tags.
My thanks to Dalex64 for this problem.
p.s. Looks like I'll be spending New Years Eve at home, as usual. If you have any good math problems to help me kill the time until midnight, please PM me.
Wizard,
My solution:
R = (pi/2)*r²/(pi/4) = 2*r²
Now we need to calculate r.
Since the diameter (of length 2*r) of the quarter-circle is also a chord of the semi-circle, we know from geometry that
2 = r²/x + x
where x is the distance along the quarter-circle's radius from the edge of the quarter-circle to the chord. A bit of geometry tells us that
x = 1 - r*sqrt(2)
Inserting this into the previous equation and solving for r² gives
r² = 1/3
Finally, plugging this into the R equation gives the result
R = 2/3
Fun puzzle... and Happy New Year!
Dog Hand
Let the radius of the red area be 1.
The point where the lower right of the semi circle intersects with the quarter circle is (1+sqrt(2)/2)rblue, (1-sqrt(2)/2)rblue.
Plugging this point into the equation for the red circle (x2 + y2 = 1), we get 3rblue2 = 1.
Ablue = pi/6
Ared = pi/4
Ablue/Ared = 2/3
Quote: teliotAs punishment, you must do the dance in this video:
This would be sooo much better in cargo shorts.
Quote: teliotOne of my favorites ... without using a calculator, which is larger, pi^e or e^pi ?
To be fair, I've seen this one before (it's in Litton's Problematical Recreations).
For all non-negative real numbers x <> e, ex > xe
Proof:
Let f(x) = ln x / x
The first derivative, f'(x) = (x * (1/x) - ln x * 1) / x2 = (1 - ln x) / x2; this is 0 when x = e
The second derivative, f''(x), is negative when x = e, so x = e is a maximum for f(x)
ln e / e > ln x / x for 0 <= x <> e
Since ex is strictly increasing, eln e / e > eln x / x
(eln e)1/e > (eln x)1/x
e1/e > x1/x
(e1/e)ex > (x1/x)ex
ex > xe
Quote: WizardA semi-circle is inscribed in a quarter-circle as follows...
What is the ratio of the area of the semi-circle to the quarter-circle?
My answer appears to be similar to Teliot's:
Without loss of generality, let the quarter-circle have radius 1, and the semi-circle have radius R
Let A and B be the endpoints of the chord of the large circle that is also the diameter of the small circle
M the midpoint of AB (which is also the center of the semicircle)
O the center of the quarter-circle
The line segments from M to the two tangent points have length R and are perpendicular to the sides of the quarter-circle, so OM = R sqrt(2) / 2
OA = OB = 1, and MA = MB = R/2, so OMA and OMB are (side-side-side) congruent, which means angle OMA is a right angle
Pythagorean Theorem: MA = sqrt(1 - 2 R2)
MA is also a radius of the semi-circle, so R = sqrt(1 - 2 R2)
R2 = 1 - 2 R2
R2 = 1/3
The area of the quarter-circle = 1/4 PI
The area of the semi-circle = (PI x 1/3) / 2 = 1/6 PI = 1/4 PI x 2/3 = 2/3 the area of the quarter-circle


