Thread Rating:
Poll
 | 3 votes (13.04%) | ||
 | 4 votes (17.39%) | ||
 | 7 votes (30.43%) | ||
 | 2 votes (8.69%) | ||
 | 2 votes (8.69%) | ||
 | 5 votes (21.73%) | ||
 | 1 vote (4.34%) | ||
 | 4 votes (17.39%) | ||
 | 7 votes (30.43%) | ||
 | 6 votes (26.08%) |
23 members have voted
Let's have an example. You have $25. You play a game where you have a 49% chance to win $1 and a 51% chance to lose $1. What is the probability you can survive 100 bets without going broke?
I know it would be easy to simulate this but is there any approximation formula I can use based on:
- Initial bankroll
- Probability of winning
- Number of bets required
Thank you.
Quote: RSWhy not simulate X different scenarios, graph the results, then look at graph or whatever to approximate a formula with one variable (i.e.: starting BR). Then do the same for other variables like # of spins etc.
That's easier said than done. I don't want to waste too much time on this, especially if some esoteric web site out there already has a formula.
There is a formula for figuring out the probability of reaching some target bankroll before going broke, but we're looking for one that has a limit on how many bets there are.
Looking at the Wizard's original example, but with win probability p (and loss probability q = 1-p):
Up through 25 bets, the probability of a bankroll change of (n-25) is the nth term (starting with 0) of the binomial expansion of (p+q)25.
In each subsequent bet, the probability of a bankroll change of n is p times the previous row's (n-1) + q times the previous row's (n-1), except that a term for -25 is ignored as once that is reached, the betting ends.
As usual with me, (n)C(k) is the number of combinations of n things taken c at a time; also known as combin(a,b).
The sum of the probabilities for the bankrupt point (bankroll = -25) is:
q25
25 p q26
((25)C(1) + (26)C(2)) p2 q27
(2 (25)C(1) + 2 (26)C(2) + (27)C(2)) p3 q28
(5 (25)C(1) + 5 (26)C(2) + 3 (27)C(2) + (28)C(3)) p4 q29
(14 (25)C(1) + 14 (26)C(2) + 9 (27)C(2) + 4 (28)C(3) + (29)C(4)) p5 q30
and so on, up to p37 q62, as anything larger would be more than 100 bets.
The terms correspond to something called Catalan's Triangle, but right-to-left
(i.e. normally in Catalan's triangle, row 5 is 1, 5, 9, 14, 14, but here is it 14, 14, 9, 5, 1).
However, I am not aware of a simple formula that would calculate the sum, even if you go by column (i.e. add up the (25)C(1) terms and multiply by 25, then add up the (25)C(2) terms and multiply by (25)C(2), and so on).
OK, you're serious. Got it. I can't wriggle out by saying, "You're not drunk as long as you can hold on to the floor."
But, seems to me, after 100 iterations, casino should have won 51 and player should have won 49, for a 2-unit loss for the player. Straight-line extension shows when player goes broke.
Of course, this is straight probability and a simulation could fluctuate significantly. But, OK. Let's look at some simulation results that are pretty close to your parameters. I've spent a LOT of time slicing and dicing your Baccarat simulation data (250,000 8-deck shoes). On the 20,219,242 hands you simulate, Banker wins 32,111 more hands than the player. Per 100 hands, that works out to the Banker winning 1.75 more units per 100 units bet (assuming 1 unit wagered per bet). Pretty close to my seat-of-the-pants suggestion of 2 units, right?
So, if you know the expected player loss per hand and the player bankroll, one can estimate the player's bankroll at any "finite step" one selects.
Seems so simple, I MUST be overlooking something. But, it's hard to "overlook" anything when you're holding on to the floor. However, I'm not as drunk as most tinkle peep I am, and I've got all day sober to Sunday up.
Quote: ThatDonGuyNow with Math!
That is further than I got, thank you. However, for the purposes at hand, I need a simple formula that doesn't involve a summation symbol. Approximations are perfectly fine. For example there is a formula given here: Risk of Ruin and Drawdown Calculation Tool, however it is for the case of infinite bets and a player advantage. I can't find anything based on a finite number of bets.
Quote: mipletThere are a bunch listed here. Probability of reaching a goal before going bankrupt given a time constraint is probably close to what you want.
Those are some amazing calculators but they seem to be simulation based.
using a simple transition matrix in ExcelQuote: WizardYou have $25. You play a game where you have a 49% chance to win $1 and a 51% chance to lose $1. What is the probability you can survive 100 bets without going broke?
I gets 0.019520497 for ruin (in agreement with a sim I also ran)
so 1 - (I gets) = the survival probability

also shows the complete ending distribution too
starting with many different bankrolls
for $25
like ending at 23 = 0.079604491
ending at 21 = 0.078072581
and so on (kids love that feature these days. I am not a kid anymore))
the Don Schlesinger formula is a good one to use too. I have not looked at it in some time
there is a paper that shows that method
and the Binomial Ruin Distribution
named
"The Impact of a Finite Bankroll on an Even-Money Game"
Kelvin Morin – Manitoba Lotteries Corporation
even mentions the late Alan Krigman
should come up in Google
<<<<< >>>>>
I thinks BruceZ has tackled that B4 2 (maybe even with some R code)
maybe knots
BruceZ still rocks around Chicago I thinks
Sally pretty
added:
my online folder (link in my blog) has the Alan Krigman Excel sheet for
I) Survival criterion -- 100 rounds
Risk of ruin = 2.0124%
Prob of survival = 97.9876%
so a small error is there
the Excel sheet is RoR-AlanK.xls
free to download
have fun!
Quote: LuckyPhowBut, seems to me, after 100 iterations, casino should have won 51 and player should have won 49, for a 2-unit loss for the player. Straight-line extension shows when player goes broke.
However, that includes, for example, the bank winning 40 of the first 55 hands, and then the player winning 34 of the last 45. You never get to those last 45 hands because, after the first 55, you won 15 and lost 40, so you have lost your entire bankroll.
That is the entire point of this problem - how often do you reach the "25 more losses than wins" point in 100 hands?
Bankroll = $25
AvgBet = 1
OriginalSD = 1*1 = 1
EV(100 trails) = (100*1)*(-.02) = -2
SD(100 trials) = Sqrt(100) * 1 = 10 * 1 = 10 ... 2SD = 20
So in 100 trials one would expect to lose $2 +/- $20... Therefor with 95% confidence one would not bust on a $25 bankroll.
From this we know there's a chance to go broke between 2 and 3 Standard Deviations. So between 95% and 99% confidence intervals. Plot the point and you should be able to find your confidence?
Yeah didn't exactly answer the question, but maybe something more to think about or something? Yeah or something... I'm gonna go with that =P.
I get that, too! But being me I had to do it my way. Here's my result:Quote: mustangsally... I gets 0.019520497 for ruin ...
Calculating for initial bankroll of 25 wager of 1 for 100 bets with 0.49 probability of winning 1 for each bet, else losing.
Probability of bust: 0.019520496908388644
LIke mustangsally's work, mine also has a compete breakdown of possible results if you care to examine the result array.
<!doctype html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Free Play Resolved</title>
</head>
<body>
<script>
const b = 25; //bankroll
const wp = 0.49; //probabilty of winning
const lp = 1 - wp; //probability of losing
const n = 100; //number of bets to process
var bp = []; //bankroll amount probability
//Initialize the bankroll probability array
for (let i=0;i<=b+n;i++) {bp=0;}
bp = 1;
document.write("<p>Calculating for initial bankroll of "+b+" wager of 1 for "+n+" bets with "+wp+" probability of winning 1 for each bet, else losing.</p>");
for (let bet=1;bet<=n;bet++){ //For each bet
let br = bp.slice(0); //create a copy to process the bet
for (let i=Math.max(b-bet+1,1);i<b+bet;i++) { //for each possibility where bankroll > 0
if (bp > 0 ) { //act if possibility > 0
//Allocate the current possibiliy to win and loss
br[i-1] += bp * lp;
br[i+1] += bp * wp;
br -= bp;
}
}
bp = br; //Make the working copy the current data
}
document.write("<p>Probability of bust: "+bp[0]+"</p>");
</script>
</body>
</html>
Coding got munched by the spoiler tag. Oh well, still valid.
Quote: mustangsally
using a simple transition matrix in Excel
I gets 0.019520497 for ruin (in agreement with a sim I also ran)
there is a paper that shows that method and the Binomial Ruin Distribution named
"The Impact of a Finite Bankroll on an Even-Money Game"
Kelvin Morin – Manitoba Lotteries Corporation
I get the same number, which is not surprising as my code is pretty much the same as her spreadsheet.
Morin's paper is here (makes sense that UNLV would have it).
However, the formula requires calculating two integrals:
P(ruin) = F( (r + 1/2 - np) / sqrt(npq) ) + F( (r - 1/2 - nq) / sqrt(npq) ) exp( 2b(q-p) / (1-(p-q)2 )
where b = the bankroll (in our case, 25)
n = the maximum number of bets (in our case, 100)
p = the win probability (in our case, 0.49)
q = the loss probability = 1 - p (in our case, 0.51)
r = the "ruin point" = (n - b) / 2 (in our case, 37.5. although I think it's supposed to be an integer)
and F(x) = the area underneath the normal distribution curve for values < x;
this is 1 / sqrt(2 PI) * the integral for u from (-infinity) to x of exp(-u2 / 2) du
Using a straightforward approximation for the integrals (starting at the maximum value, calculating the value at intervals of 0.1 until the sum didn't appear to get any larger (in this case, 200), adding them up, and multiplying by the interval width), I got a ruin of 0.018091637 for r = 37 and 0.023785798 for r = 37.5 (which is (100 - 25) / 2). The correct value appears at about r = 37.13783.
Since calculating the integrals is going to require approximation, you might as well calculate the values using a matrix; note that the size of the matrix varies approximately in proportion to the square of the maximum number of bets.
Or, as BleedingChipsSlowly points out, since we're not interested in the intermediate step values, you only really need a one-dimensional matrix (not two, as the numbers in the odd positions are calculated from the numbers in the adjacent even positions, and then the numbers in the even positions are calculated from the numbers in the adjacent odd positions, going back and forth).
Quote: ThatDonGuyHowever, that includes, for example, the bank winning 40 of the first 55 hands, and then the player winning 34 of the last 45. You never get to those last 45 hands because, after the first 55, you won 15 and lost 40, so you have lost your entire bankroll.
That is the entire point of this problem - how often do you reach the "25 more losses than wins" point in 100 hands?
I agree. As several of the other replies seem to mutually confirm, the answer is one seldom (95% probability) encounters such an extreme example as the one you posit. But, it can happen.
Now, back to the Wiz's original issue: a formula for Internet casino bonuses that shows the probability of ruin in a finite number of steps. Is this like the, "Get $$$ welcome bonus" (but it's only available after the player deposits $$$ and plays no fewer than ### hands)? Ideally, the Internet casino (I'm guessing here) would like the player to lose most -- but not all (avoiding "ruin") -- of her buy-in, but then gets the bonus, continues to play, and -- hopefully -- stays as a "regular" at the site. Hey, Wiz! Am I even close to how Internet casinos want to use your formula?
But, as the player gets closer to "ruin" before qualifying for the (anticipated) bonus, the casino gets closer to losing a (new?) player who leaves feeling cheated. Seems to me the Internet casino would most of all want to avoid that. Keeping risk of ruin low for the player also keeps low the Internet casino's risk of losing the player as a customer.
Quote: mustangsallyadded:
for a very nice approximation formula
my online folder (link in my blog) has the Alan Krigman Excel sheet
(uses Don Schlesinger's trip risk of ruin formula that is very accurate as the number of trials increases)
I) Survival criterion -- 100 rounds
Risk of ruin = 2.0124%
Prob of survival = 97.9876%
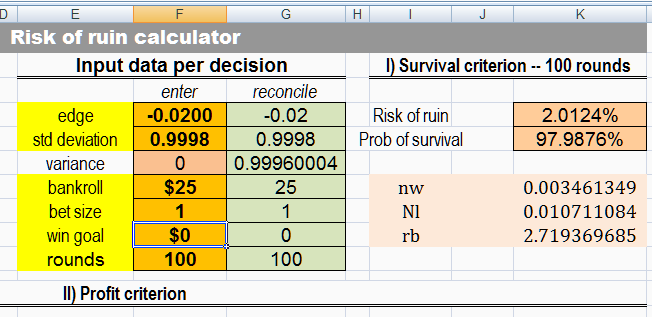
so a small error is there
the Excel sheet is RoR-AlanK.xls
Quote: RomesCouldn't you try to simplify it further? What's the house edge of the game? 2%? Variance = 1 (given you can only win or lose $1). Why not just run the EV +/- SD to find the ruin probability?
The question you seem to be answering is what is the probability of being below zero after 100 hands, assuming you could play on credit if you feel below before.
However, I'm asking what are the chances of ruin at any point. It could happen the player is ruined on hand #90, plays on credit and wins, and finishes 5 units up. He would show a success based on just the result after 100 hands, but if he couldn't get a marker, then he would have busted out.
Quote: LuckyPhowNow, back to the Wiz's original issue: a formula for Internet casino bonuses that shows the probability of ruin in a finite number of steps. Is this like the, "Get $$$ welcome bonus" (but it's only available after the player deposits $$$ and plays no fewer than ### hands)? Ideally, the Internet casino (I'm guessing here) would like the player to lose most -- but not all (avoiding "ruin") -- of her buy-in, but then gets the bonus, continues to play, and -- hopefully -- stays as a "regular" at the site. Hey, Wiz! Am I even close to how Internet casinos want to use your formula?
Actually, the way Internet casino bonuses usually work is they give it to you after you make a deposit. However, to make a withdrawal you have to play through the combined deposit and bonus x number of times. Then, if you survive all the play, they will deduct the bonus from your account and you can withdraw the rest.
Quote: mustangsallythe Don Schlesinger formula is a good one to use too.
Thanks. I must have brushed over that too quickly when I read his book. I just posted it to my private Facebook account.
I'm very impressed at the formula but is probably too advanced to implement in a simple JavaScript calculator.
Quote: WizardActually, the way Internet casino bonuses usually work is they give it to you after you make a deposit. However, to make a withdrawal you have to play through the combined deposit and bonus x number of times. Then, if you survive all the play, they will deduct the bonus from your account and you can withdraw the rest.
It's not whether you win or lose; it's whether or not you had a good bet.
Based on what you said how internet casino bonuses work, wouldn't you agree that the free money is not free at all and in fact would reduce you actual odds of winning? Are people expected to be so foolish and believe that the casinos like the ads say are willing to give you $1,100.00 free dollars so you could beat their asses?
If whether or not you had a good bet is what actually matters, (your own words) this bonus stuff sounds more like a dumb sucker bet. Being who you claim to be shouldn't the AP advice be to stay clear of these bonuses?
Quote: WizardActually, the way Internet casino bonuses usually work is they give it to you after you make a deposit. However, to make a withdrawal you have to play through the combined deposit and bonus x number of times. Then, if you survive all the play, they will deduct the bonus from your account and you can withdraw the rest.
Well, that's disappointing. I had thought you were playing for the entire amount, sort of "earning" the bonus amount with the playthrough. At the end they take back the bonus amount? Wow.
So if I deposit 500, they match 500, I play through 30x the total amount, and end up with, say, a balance of $550 (already an incredibly lucky situation). If what you're saying is true, I didn't win $50, I lost $450, once they take their bogus award back.
I'm appalled I ever even tried this, which I did with Bova da a couple times last year. Never again.
Are they all like this? What a scam.
Quote: WizardI'm very impressed at the formula but is probably too advanced to implement in a simple JavaScript calculator.
Not really. Here's some pseudocode:
// P - probability of winning
// B - initial bankroll
// N - max number of bets
Q = 1 - P // Q - probability of losing
V = 4 * Q * P // V - variance of the random variable
E = P - Q // E - player edge
X0 = (-B - N * E) / SQRT(N*V) - 0.005
X1 = (-B + N * E) / SQRT(N*V) - 0.005
F0 = EXP(-(X0*X0)/2) / SQRT(2*PI) * 0.01
F1 = EXP(-(X1*X1)/2) / SQRT(2*PI) * 0.01
for (Step = 1; Step <= 500; Step++)
{
X0 = X0 - 0.01
F0 = F0 + EXP(-(X0*X0)/2) / SQRT(2*PI) * 0.01
X1 = X1 - 0.01
F1 = F1 + EXP(-(X1*X1)/2) / SQRT(2*PI) * 0.01
}
Ruin = F0 + F1 * EXP(-2 * B * E / V)
It took me a while to get this to work with any degree of accuracy - until I realized that I was trying to calculate the variance using a loss value of 0 rather than -1.
The loop approximates the area underneath the normal distribution curve to the left of the given X value, using strips of width 0.01; the smaller the width, the more accurate you can get, but the more steps you need to reach a stable value.
Quote: JoeshlabotnikIsn't the EV of a series of plays the same whether the RoR is 0% or 99%? Or are you saying that your finite number of steps is a mandated minimum?
At least if you're ruined you don't have to give the bonus back.
Quote: WizardThanks. I must have brushed over that too quickly when I read his book. I just posted it to my private Facebook account.
I'm very impressed at the formula but is probably too advanced to implement in a simple JavaScript calculator.
Do we have to be friends with you to see it?
I think I can take a crack at writing a calc for something like that.
Quote: beachbumbabsWell, that's disappointing. I had thought you were playing for the entire amount, sort of "earning" the bonus amount with the playthrough. At the end they take back the bonus amount? Wow.
Sometimes they let you keep it, sometimes they don't. The calculation for the value of the bonus is a lot easier if it is cashable. It gets complicated if it isn't.
Quote:So if I deposit 500, they match 500, I play through 30x the total amount, and end up with, say, a balance of $550 (already an incredibly lucky situation). If what you're saying is true, I didn't win $50, I lost $450, once they take their bogus award back.
That is correct. However, they would argue that the extra $500 allowed you to play longer. Without it, you would have busted out earlier and wouldn't have the $50.
Quote:I'm appalled I ever even tried this, which I did with Bova da a couple times last year. Never again.
Are they all like this? What a scam.
Again, not all bonuses are like this. I hate to throw out percentages, but you so both kinds frequently. You have to parse the terms pretty carefully to see if the bonus is cashable or not, which I don't care for.
However, the non-cashable bonuses are not as bad as you think. Let's look at your example. After you complete your play you plop down your $550 on a single number in single-zero roulette. If you win, great, cash out. If not, c'est la vie. The value of your situation before the spin is =
(1/37)*(36*550 - 500) + (36/37)*0 = $521.62. That is a lot better than $50.
Quote: ThatDonGuyNot really. Here's some pseudocode:
// P - probability of winning
// B - initial bankroll
// N - max number of bets
Q = 1 - P // Q - probability of losing
V = 4 * Q * P // V - variance of the random variable
E = P - Q // E - player edge
X0 = (-B - N * E) / SQRT(N*V) - 0.005
X1 = (-B + N * E) / SQRT(N*V) - 0.005
F0 = EXP(-(X0*X0)/2) / SQRT(2*PI) * 0.01
F1 = EXP(-(X1*X1)/2) / SQRT(2*PI) * 0.01
for (Step = 1; Step <= 500; Step++)
{
X0 = X0 - 0.01
F0 = F0 + EXP(-(X0*X0)/2) / SQRT(2*PI) * 0.01
X1 = X1 - 0.01
F1 = F1 + EXP(-(X1*X1)/2) / SQRT(2*PI) * 0.01
}
Ruin = F0 + F1 * EXP(-2 * B * E / V)
It took me a while to get this to work with any degree of accuracy - until I realized that I was trying to calculate the variance using a loss value of 0 rather than -1.
The loop approximates the area underneath the normal distribution curve to the left of the given X value, using strips of width 0.01; the smaller the width, the more accurate you can get, but the more steps you need to reach a stable value.
You, sir, are a gentleman and a scholar. Very clever! It is too advanced for the simple JavaScript application this is for but I'm very impressed. If you're ever in Vegas, I owe you a beer. You'll have to remind me, though. I will forget the promise in about 72 hours.
Quote: Wizard
You, sir, are a gentleman and a scholar. Very clever! It is too advanced for the simple JavaScript application this is for but I'm very impressed. If you're ever in Vegas, I owe you a beer. You'll have to remind me, though. I will forget the promise in about 72 hours.
Actually, that's two now, and I was just in Vegas a month ago.
But never mind about the beers (they pretty much all taste the same to me anyway) - what I would like is, could somebody tell me where the Double Blackjack table is located at GVR?
IMO you have a closed mind about AP. One of the best and most lucrative promotions at any casino was online and everyone (that I know of) got paied estimated over 1 million in a few hours with very little risk. Look up the....007 roulette promotion @ casino-on-net.Quote: blackholeIt's not whether you win or lose; it's whether or not you had a good bet.
Based on what you said how internet casino bonuses work, wouldn't you agree that the free money is not free at all and in fact would reduce you actual odds of winning? Are people expected to be so foolish and believe that the casinos like the ads say are willing to give you $1,100.00 free dollars so you could beat their asses?
If whether or not you had a good bet is what actually matters, (your own words) this bonus stuff sounds more like a dumb sucker bet. Being who you claim to be shouldn't the AP advice be to stay clear of these bonuses?
Also research online casino bonuses. There's money to be made and people are doing ^^^it.
Not all casinos are trustworthy but if you do your research there's less risk of them no paying.
If you only play bonuses and promotions that have a significant advantage you can afford to not getbpaied. I don't suggest depositing large amounts. Keep your cash out amounts low at first, Do.
Quote: beachbumbabsWell, that's disappointing. I had thought you were playing for the entire amount, sort of "earning" the bonus amount with the playthrough. At the end they take back the bonus amount? Wow.
So if I deposit 500, they match 500, I play through 30x the total amount, and end up with, say, a balance of $550 (already an incredibly lucky situation). If what you're saying is true, I didn't win $50, I lost $450, once they take their bogus award back.
I'm appalled I ever even tried this, which I did with Bova da a couple times last year. Never again.
Are they all like this? What a scam.
Not a scam. Very beatable, "phantom bonus". When I first started, it was all cashable bonuses. The first guys I remember doing phantom was some of the Playtech guys started going that way. Some guys started "sticky" bonuses, and then phantoms. I just don't mess with it anymore. Knocking out us Americans screwed up the whole deal.
When I first discovered the online gravy train in about 2001, I never left my bedroom. It was great. I could lose $100 before I brushed my teeth. I shoulda got rich. Some people did.
function pRuin(bankroll,bets,pWin) {
const pLoss = 1 - pWin;
var bp =[];
for (let i=0; i<=bankroll+bets; i++) {bp[i]=0;}
bp[bankroll] = 1;
for (let bet=1; bet<=bets; bet++) {
let br = bp.slice(0);
for (let i=Math.max(bankroll-bet+1,1); i<bankroll+bet; i++ ) {
if (bp[i] > 0) {
br[i-1] += bp[i] * pLoss;
br[i+1] += bp[i] * pWin;
br[i] -= bp[i];
}
}
bp = br;
}
return bp[0];
}
The solution quickly provides an exact answer, not an estimate. Is it too simple to be acceptable? Not math-heavy enough for this forum?
<!doctype html>
<html><head><script>
function pRuin(bankroll,bets,pWin) {
const pLoss = 1 - pWin;
var bp =[];
for (let i=0; i<=bankroll+bets; i++) {bp[i]=0;}
bp[bankroll] = 1;
for (let bet=1; bet<=bets; bet++) {
let br = bp.slice(0);
for (let i=Math.max(bankroll-bet+1,1); i<bankroll+bet; i++ ) {
if (bp[i] > 0) {
br[i-1] += bp[i] * pLoss;
br[i+1] += bp[i] * pWin;
br[i] -= bp[i];
}
}
bp = br;
}
return bp[0];
}
</script></head><body><script>
document.write(pRuin(25,100,0.49));
</script></body></html>
Quote: BleedingChipsSlowlyThis is the Javascript solution algorithm I posted, reworked as a function and with character escapes added so that the site posting reflects the text as intended.
The solution quickly provides an exact answer, not an estimate. Is it too simple to be acceptable? Not math-heavy enough for this forum?
Too simple? Not math-heavy enough? Not at all - plus, bp[1] through bp[bankroll + bets] end up with the probabilities of ending with each possible ending value, if you're interested in that.
The only "problem," if you can call it that, is, you have to build an array for each bet, and it increases in size from one bet to the next. For low numbers of bets, that's not going to be a problem, but what happens when you have a large number of bets? (I think it comes down to, just when does the Java VM garbage collect the br array created in each iteration of the bet for loop.)
Then again, you can get around that by having a single array of size (bankroll + bets + 1), and alternating between calculating the odd-index values and the even-index values (remembering to add elements 0 and 1 to get the new value for element 0). In this case, you have to remember that, at the end, half of the values in the array (the ones not calculated in the final bet step) are invalid.
Thanks for your thoughtful commentary, your points are well taken. Actually, the array size is initialized for all bets, it doesn't expand. I thought of expanding the array for each bet but decided against that for simplicity. Likewise, the code design assumes the VM garbage collection works well. I tend not to code solutions for problems unless they present themselves. As to a practical limitation on the number of bets I had no problem processing 10000 in less than a second. That represents more than 15 hours of rabid gambling by my reconing, which I think covers the problem domain. A million bets does not precess well, but that would represent a more than a week of nonstop gambling. I hardly think free play offers are made with the intention of providing patrons with more than a brief time of play.Quote: ThatDonGuyQuote: BleedingChipsSlowlyThis is the Javascript solution algorithm I posted, reworked as a function and with character escapes added so that the site posting reflects the text as intended.
The solution quickly provides an exact answer, not an estimate. Is it too simple to be acceptable? Not math-heavy enough for this forum?
Too simple? Not math-heavy enough? Not at all - plus, bp[1] through bp[bankroll + bets] end up with the probabilities of ending with each possible ending value, if you're interested in that.
The only "problem," if you can call it that, is, you have to build an array for each bet, and it increases in size from one bet to the next. For low numbers of bets, that's not going to be a problem, but what happens when you have a large number of bets? (I think it comes down to, just when does the Java VM garbage collect the br array created in each iteration of the bet for loop.)
Then again, you can get around that by having a single array of size (bankroll + bets + 1), and alternating between calculating the odd-index values and the even-index values (remembering to add elements 0 and 1 to get the new value for element 0). In this case, you have to remember that, at the end, half of the values in the array (the ones not calculated in the final bet step) are invalid.
Quote: WizardI've been tasked with assessing the general value of Internet casino bonuses given certain parameters. I find it is necessary to have a general formula for the probability of ruin. I've seen such formulas before but they all seem to be based on infinite steps until a given goal is met or ruin.
Wow! For me, this has been a fascinating, interesting, educational thread, and I wanted to take a minute to thank the many Stat Wizards for sharing. Thanx for all the detailed back-up calculations that helped explain what you were saying. And, the external references. (My first read of the Morin article says it needs more careful examination, but thanx MustangSally. Haven't yet done justice to miplet's web reference, but what I saw says, "Come back when you can visit longer.") You know who you are, but thanx to ThatDonGuy who tried to steer me on a better tack, and BleedingChips and Romes, and anyone else I missed. I feel like I just happened to step into the faculty lounge where everyone was discussing a problem posed by last week's guest lecturer, and, what a discussion it is!
As for the Wiz, I sorta feel like I'm the dog riding in the back of the pick-up truck. I'm not quite sure where he's going or why. But, I'm sure enjoying the ride. And, once we get there, it'll probably be even more fun, don'cher know?


