Seven people are each given a hat that is either red or blue. (Not every hat is necessarily the same color.) Each person can see only the other six hats; there is no way for anyone to communicate with anyone else. At a given signal, each person will hold up one of three cards - red, white, or blue. The group "wins" if (a) at least one person's card matches his hat, and (b) no one holds up a non-white card that does not match his hat. Note that nobody can see anyone else's card choice, or even when the choice was made; each person receives no information other than what color hat each other person is wearing, although they do know which person has which hat.
What is the best strategy?
When I first heard the problem, my answer was:
Persons 1-4 are told, "If the other three people in 1-4 are wearing the same color hat, choose the other color; otherwise, choose white."
Persons 5-7 are told, "If the colors of the hats on 1-4 are a 3-1 split, choose white; otherwise, use the same strategy - if the other two people in 5-7 are wearing the same color hat, choose the other color; otherwise, choose white."
The 1-4 group can be split into 4-0 2 ways, 3-1 8 ways, and 2-2 6 ways.
If it is 4-0 (let's say red), each of them will see a red hat and choose blue, and lose.
If it is 3-1, the ones with red hats will see 2 red and 1 blue, and choose white; the one with the blue hat will see 3 red hats and choose blue; 5-7 will see 3 red hats and 1 blue hat on 1-4 and choose white; this is a win.
If it is 2-2, each one will see hats of both colors and choose white; 5-7 can be a 3-0 split 2 ways (where each of them will see two hats of the same color, choose the other color, and lose) and a 2-1 split 6 ways (where the two with the matching color will see one of each and choose white, the other will see two of the same color and choose the other one, and they win).
The probability of a win is 8/16 + 6/16 x 6/8 = 25/32, or slightly better than 3/4.
This takes up 16 perms and so leaves 112. Co-incidentally this is 7*16!
I am guessing in most cases only one person votes (and by definition can only be 50:50) but if they get it wrong then so does everyone else. The trick is to find a method of assigning the remaining perms so this happens.
Note: Answer and solution updated at 5:33 PM PST.
Firstly you need to have heard of Hamming Codes (e.g. see https://en.wikipedia.org/wiki/Hamming%287,4%29 ) they have a property that starting with 4 original bits but transmitting 7, if one bit goes wrong then you can work out which one it is. Thus there are 16 Hamming Codes and if we change one bit can calculate which one we started from. For each code there is the correct one and seven associated numbers (i.e. flip one bit).
Thus if we only change one bit, all 128 possibilities are covered.
Number each player 1 thru 7. The rule for each player is that if, given the six they can see, find out whether it might be one of the sixteen Hamming codes. The simplest case is if they see six all the same colour.
Then they guess the opposite of what forms the code - i.e. seeing six Red guess Blue.
In this way if the result is one of the codes, everyone will guess wrong. However if it is (say) 6-1 then six people will keep quiet and only one will guess correctly. The column where you find the corresponding value 1-128 will indicate which player calls and which code was thought possible.
Since sixteen times everyone gets it wrong, and all other times only one votes and gets it right, so chance = 7/8.
| 0000000 | 0 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1111111 | 127 | 63 | 95 | 111 | 119 | 123 | 125 | 126 |
| 1110000 | 112 | 48 | 80 | 96 | 120 | 116 | 114 | 113 |
| 1001100 | 76 | 12 | 108 | 92 | 84 | 80 | 78 | 77 |
| 0111100 | 60 | 124 | 92 | 76 | 68 | 64 | 62 | 61 |
| 0101010 | 42 | 106 | 74 | 58 | 50 | 46 | 44 | 43 |
| 1011010 | 90 | 26 | 122 | 106 | 98 | 94 | 92 | 91 |
| 1100110 | 102 | 38 | 70 | 118 | 110 | 106 | 104 | 103 |
| 0010110 | 22 | 86 | 54 | 38 | 30 | 26 | 24 | 23 |
| 1101001 | 105 | 41 | 73 | 121 | 113 | 109 | 107 | 106 |
| 0011001 | 25 | 89 | 57 | 41 | 33 | 29 | 27 | 26 |
| 0100101 | 37 | 101 | 69 | 53 | 45 | 41 | 39 | 38 |
| 1010101 | 85 | 21 | 117 | 101 | 93 | 89 | 87 | 86 |
| 1000011 | 67 | 3 | 99 | 83 | 75 | 71 | 69 | 68 |
| 0110011 | 51 | 115 | 83 | 67 | 59 | 55 | 53 | 52 |
| 0001111 | 15 | 79 | 47 | 31 | 23 | 19 | 17 | 16 |
Quote: WizardDesignate three particular people. The other four can be ignored. Of those three, if they see two of the same color hat, then pick the opposite color, otherwise pick white. This will work unless those three hats are all the same color.
If the distribution is exactly a Code then everyone will guess wrong, otherwise just one person can be one away from the Code and will get it correct. Remember the definition of the code is that given there is only one bit wrong, you can work out which was the original code. Therefore if the distribution is one away only one person can see a possible valid code. Each Code covers (n+1) combinations and n of these can be detected correctly whereas 1 can't. Thus the chance of being correct is n/(n+1).
There is a useful description in https://en.wikipedia.org/wiki/Hamming_code .
My 3/4 answer does not allow for redraws -- because there will always be at least one responder. In trying to follow the Hamm codes solution I get situations where multiple bits are wrong and I'm not sure how to treat such situations.
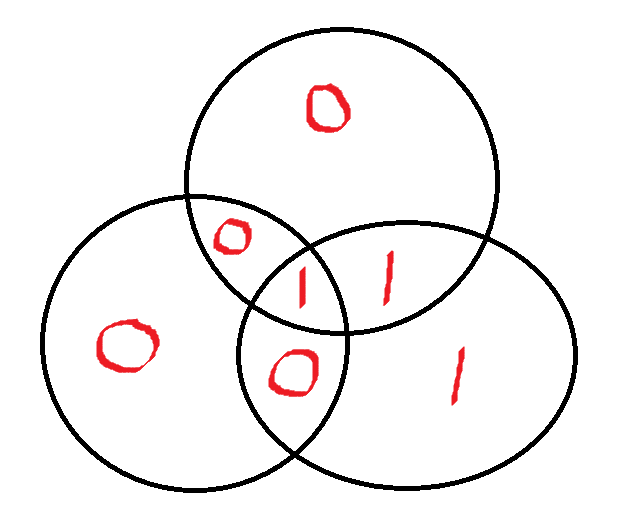
To ask it another way, what should happen if the hats were as such, using zeros and ones instead of red and blue.
Quote: ThatDonGuyHere is a variation on the 100 Hats puzzle:
Seven people are each given a hat that is either red or blue. (Not every hat is necessarily the same color.) Each person can see only the other six hats; there is no way for anyone to communicate with anyone else. At a given signal, each person will hold up one of three cards - red, white, or blue. The group "wins" if (a) at least one person's card matches his hat, and (b) no one holds up a non-white card that does not match his hat. Note that nobody can see anyone else's card choice, or even when the choice was made; each person receives no information other than what color hat each other person is wearing, although they do know which person has which hat.
What is the best strategy?
Without an opportunity to discuss strategy ("There is no way for anyone to communicate with anyone else."),
In order to get to the 7/8ths answer:Quote: Wizard...if everybody chooses white....what about 0 0 1 1 0 0 1
(i) There are 128 possible (2^7) ways the hats can be distributed., as you suggested let's use a binary notation.
(ii) The best solution is if you can come up with 16 distributions where they lose while leaving 112 where they win.
This fact is no secret, it's the only way to achieve the 7/8ths answer - it's the method of achieving this that is the puzzle.
The first scenario is fairly obvious, as it is similar to the 3-hat problem. Thus instruct anyone that sees six hats the same colour to vote the other, and if you see 5-1 keep quiet. This means that they win with any 6-1 distribution but lose with any 7-0. This creates 14 winners (0111111,1011111...1111110; 1000000..0000001) and 2 losers (1111111 0000000).
The challenge is to find sixteen numbers such that they and their seven surrounding numbers (with one bit flipped i.e. 1st thru 7th bit) cover all the permutations 0-127. They will then have the property that if the distribution is exactly a code then everyone calls it wrong, while the seven surrounding numbers with one bit flipped are winning combinations. If sixteen numbers cover all 128 combinations, then each number must either be a code or a surrounding number of one, and only one, of the codes. Thus it must be a 1-to-1 mapping from any combination to the associated code, and if you are a surrounding number only one person can be one-bit out.
In your example 0011001 you have an exact code, so everyone will see that they might be part of a code ?011001...001100? and they will all call it wrong. Everyone knows that if the actual distribution is a code then they cannot win, thus they have to assume it isn't. For instance the first person, seeing ?011001 will have to assume it's 1011001 rather than 0011001 - the logic is that if it was 0011001 he knows the 2nd person would be seeing 0?11001 and be calling it wrong.
The table I gave in the earlier answer gives all the combinations and their associated codes - but an intellectual challenge is to derive the codes for yourself!

Image 2
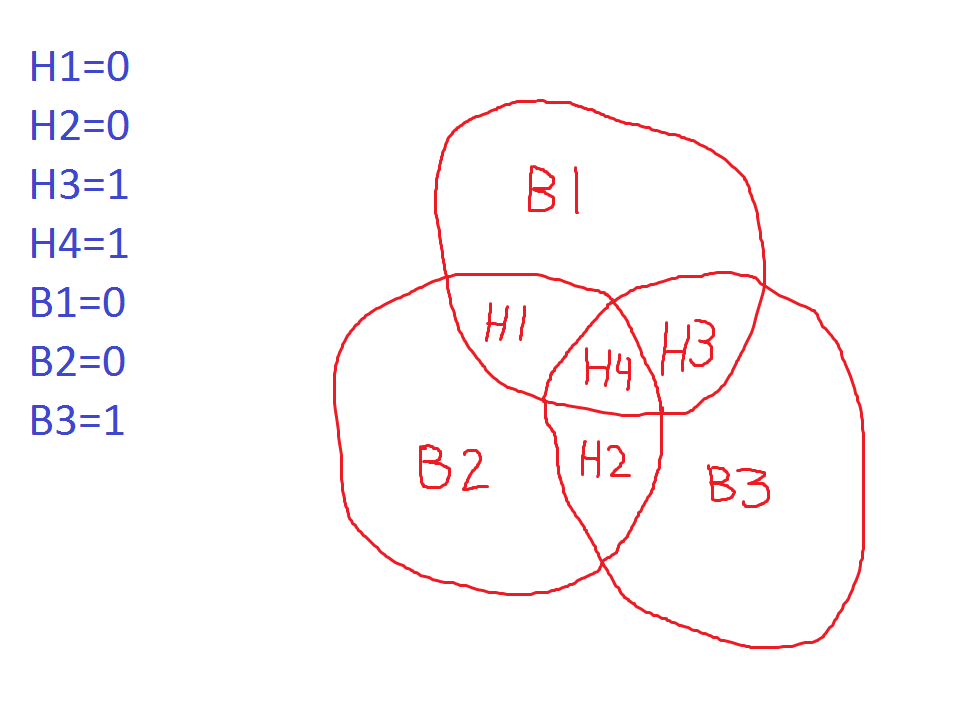
Player 1 would would think that H2 was the bit in error, which would be true if he were a zero.
Player 2 would think the same thing as player 1.
Player 3 would also think H2 was in error, which would be true if he were a one.
So, player 1 would say "zero", player 2 "zero", and player 3 "one." They would all be right and be freed.
Did I think this through correctly or was I just lucky?
Actually you were unlucky and picked a losing combination!Quote: WizardDid I think this through correctly or was I just lucky?
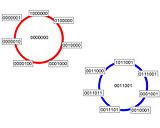
You can see two circles, one centered on 0000000 and another on 0011001 (which is one of the sixteen codes). There are 14 other similar circles, such that every combination (of the 128 possibilities) only appears once.
The logic runs as follows and is easiest to understand for 0000000 or 1111111. Essentially using the six you can see, there will be two possible combinations. If one of these is one of the code numbers (i.e. in the centre of one of the circles) then pick the other.
Assume you were 1st player, then if all the other six are 0, you could form 0000000. You know the actual distribution is either 0000000 or 1000000; however you must pick 1000000. The rationale is that if it is 1000000 then you are correct and, as it happens, none of the other players (seeing something like 1?00000) are one away from a code number so they will all keep quiet. However if it is 0000000 then everyone else will see six 0's, everyone will pick 1, thus you are destined to lose.
The similar logic applies to the code number 0011001. If this is the actual distribution then everyone will get it wrong. If you change any one of the bits, then only one person will speak up and that person will get it correct.
The sixteen circles cover all 128 possibilities. Being in the middle means everyone speaks and they all get it wrong. Being on the circle means only one person can see the code and will always call it right (by taking the code and flipping their bit). There are 7 points on the outside for each central point; this gives the 7/8 possibility answer.
Thus you were unlucky to have chosen one of the code numbers where, using correct strategy, they lose.
Given my values of P1=0, P2=0, and P3=1, the correct Hamm codes would be H1=0, H2=1, H3=1, and H4=1. I changed only H2 to zero. So, if this is supposed to work if you change just one of the Hamm codes, why was my example one of the the 12.5% of losing cases?
If H2 were flipped to 1 then my diagram 2 would sense. However, H2 wouldn't know what he is. Would he think, "This would all make sense of I were a 1, so I'll say the opposite of 0."
The simplest one is if your message was one bit (i.e. 0 or 1), then send three bits. If the message is "0" then send "000" and if "1" then send "111". You can then see that if you receive 000 001 010 or 100 then you work out the original message was 0, and 011 101 110 and 111 correspond to 1.
Skip this next paragraph if you like
As an aside think of a problem where you're asked how many unit spheres are needed to cover al the points of a unit cube. The cube has 8-points from (x=0,y=0,z=0)...(1,1,1), corresponding to the sent message. The points nearest (0,0,0) correspond to the original message 0 and can be thought off as covered by a three-dimensional sphere at the origin. Similarly there is a sphere at (1,1,1) covering the message 1. As it happens the two spheres manage to cover all eight of the points with no duplications. Also every point on the cube is only associated with one sphere. Thus given any point on the cube we know it is either in or on Sphere 0 or Sphere 1.
Going back to the hats, with three hats it is intuitive to create a rule that if you see two hats of the same colour then pick the other colour. This wins when they're 2-1 and loses when 3-0. What isn't so obvious is this corresponds to saying that if you're on the edge of a sphere (0) 001,010,100 (1) 011,101,110 then only one player will see two-hats, call it correctly and the team wins, while if you're in the centre (000 111) everyone will call it wrong.
Obviously player 1, on seeing two identical hats, doesn't know for certain whether it's 000 or 100, but knows the best strategy is to assume it's 100. This is mathematically similar to saying that if the player could make one of the Hamming Codes (000 or 111 in this case) then flip his bit and call that. Thus Player 1, seeing ?00, knows it could be 000, flips his bit to 100 and calls "1". If it is 100 then Player 2 sees 1?0 and keeps quiet, and Player 3 sees 10? and also keeps quiet, and the team can win. While accepting if it is 000 then the team is destined to lose as everyone will have seen two 0's and called 1.
Note there are two Hamming Codes (000 and 111) and for each code this is the one combination where everyone calls, while flipping each bit in turn creates three combinations where only one person calls and the team wins.
Now moving to seven players, you use a similar idea except you need 16 Hamming Codes. (These codes use 7-bits to send 4-bit messages.) This creates 16 spheres that cover the entire 128 combinations. Similar logic applies: for each code this is the combination where everyone calls, while flipping each bit in turn creates seven combinations where only one person calls and the team wins.
I posted a table with all 128 possible settings and showed which player called and the associated Hamming Codes. The first line was 0 (all lose) 64 32 16 8 4 2 1 (one calls, team wins). So with 0100000=32, only player 2 can see a possible code and calls. Thus you can see which (112 in total) combinations enable the players to win and the 16 Hamming Codes where they can't.
If you saw my previous picture this is what the red circle showed - the combinations that won and the centre of the circle where they lost. The blue circle was a different Hamming Code showing the same idea.
The answer is to provide the players with a list of the 16 Hamming Codes and give them the instructions if the player's colour/bit/hat could complete one of the Hamming Codes then flip his colour/bit and call that. Your example, bad luck P=1/8, was one of the codes; so the players, using optimal strategy, were destined to lose for that combination.
Quote: WizardLet me ask something about the original question. What happens if everybody chooses white?
The group "wins" if (a) at least one person's card matches his hat, and (b) no one holds up a non-white card that does not match his hat.
If everybody chooses white, they lose.
| 0000000 | 0 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1111111 | 127 | 63 | 95 | 111 | 119 | 123 | 125 | 126 |
| 1110000 | 112 | 48 | 80 | 96 | 120 | 116 | 114 | 113 |
| 1001100 | 76 | 12 | 108 | 92 | 84 | 80 | 78 | 77 |
| 0111100 | 60 | 124 | 92 | 76 | 68 | 64 | 62 | 61 |
| 0101010 | 42 | 106 | 74 | 58 | 50 | 46 | 44 | 43 |
| 1011010 | 90 | 26 | 122 | 106 | 98 | 94 | 92 | 91 |
| 1100110 | 102 | 38 | 70 | 118 | 110 | 106 | 104 | 103 |
| 0010110 | 22 | 86 | 54 | 38 | 30 | 26 | 24 | 23 |
| 1101001 | 105 | 41 | 73 | 121 | 113 | 109 | 107 | 106 |
| 0011001 | 25 | 89 | 57 | 41 | 33 | 29 | 27 | 26 |
| 0100101 | 37 | 101 | 69 | 53 | 45 | 41 | 39 | 38 |
| 1010101 | 85 | 21 | 117 | 101 | 93 | 89 | 87 | 86 |
| 1000011 | 67 | 3 | 99 | 83 | 75 | 71 | 69 | 68 |
| 0110011 | 51 | 115 | 83 | 67 | 59 | 55 | 53 | 52 |
| 0001111 | 15 | 79 | 47 | 31 | 23 | 19 | 17 | 16 |
As I asked before, how did you arrive at that table? Also would this table work:
00000000
11000000
00110000
00001100
00000011
10101000
00101010
10001010
and then the eight mirror opposites of the above.
Remember if you pick the right codes, they provide 16 losers and should leave 112 winners. Thus the optimal solution only needs 16 codes. Each code has 7 (i.e. each bit flipped) one-away winners; 16 Codes with 7 "radii" provides 112 end-points. To provide full coverage the end point of each radii has to be unique, since you need 112 winners. Thus you can't have a situation where any combination can be one-away from two different codes.
The problem with your solution is that you can't have a code with two 1's. Assuming that 0000000 is one code, then if 1100000 was a code 0100000 would be one away from two codes. In this case both 1st (?100000~1100000) and 2nd (0?00000~0000000) players would call their colour correctly. Thus some combination, somewhere else, hasn't got an end-point.
Firstly any one-aways cannot be a Code; we know all other Codes have 3 or 4 1's so the only ones to worry about are 111+1000,0100,0010,0001. So you can't have a code which is exactly one-bit different from an existing code.
Secondly looking at one-aways of 0110000,1010000 and 1100000 this prevents us choosing another code of 011+1000,0100,0010,0001 etc. In other words you cannot have a code which is exactly two-bits different from an existing code (essentially this means two radii would land up having common end points).
This knocks out 1111000 1110100 1110010 1110001, 0111000 0110100 0110010, 1011000 1010100 1010010, 1101000 1100100 1100010 and all opposites.