Math Question

Would anyone know the odds to the following problem?

There are 26 rocks labeled A through Z. What are the odds one would pick rocks A through I, before one would pick a rock labeled X, Y or Z? You pick one rock at a time and you put the rock you picked back in the mix. A rock can be picked more than once, and it doesn't matter if you pick a rock J through W. Thanks

this is almost like the very last math question i answered way back in the school days, and i got that one wrong
i was such a math dunce back then

i see this as 26 Keno balls
we are trying to draw, in any order, the numbers 1 thru 9 (each at least 1 time)
B4 the numbers 24,25 or 26 is drawn 1 time

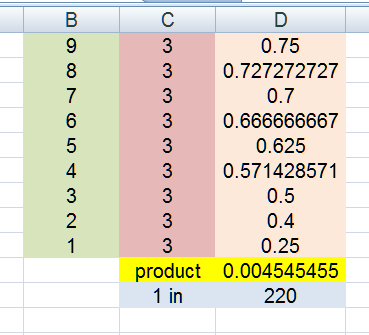
the odds against (i get now) are 219 to 1
that makes the probability of success 1 in 220 or 1/220

i made a simple 11x11 transition matrix in Excel just to check

and... check


i would think it would take some time to complete the set
as the expected number of draws to either win or lose
looks to b 8.627272727 (easily calculated)

augustBE later on that
(73.5531746)

now to get ready for the baseball game tonite at the Big A
Sally

We can ignore the rocks J through W in this case.
The problem becomes:
What is the probability of drawing one of the nine rocks A through I before any of X,Y,Z, then drawing one of the eight rocks in A through I other than the one already drawn before any of X,Y,Z, then drawing one of the seven rocks in A through I other than the two already drawn before X,Y,Z, and so on.

This is (9 / (9 + 3)) x (8 / (8 + 3)) + (7 / (7 + 3)) + ... + (2 / (2 + 3)) + (1 / (1 + 3))
= (9 x 8 x 7 x ... x 2 x 1) / (12 x 11 x 10 x ... x 5 x 4)
= (3 x 2 x 1) / (12 x 11 x 10) = 1 / 220.

Imagine that we keep drawing letters until we have drawn each of the 12 letters A-I and X-Z at least once. We record the order that these letters make their first appearance. Since each of those 12 letters have the same probability, all 12! possible sequences are equally probable. We win if we get a sequence of all the letters A-I in any order followed by a sequence of the letters X-Z in any order . Since there are 9! arrangements of A-I and 3! arrangements of X-Z, there are 9!3! winning sequences, so the probability is 9!3!/12! = 1/220.

Thank you everyone for the results, but I think I relayed question wrong. Going with Bruce's example, I would like to know what the odds of drawing those letters A through I before either of the letters X, Y or Z are drawn, not all three X, Y and Z drawn. 1 in 220 seems about right, maybe I'm missing what Bruce is saying. Thanks again.

I get mustang's explanation. And all arrived same answer thank you.

Quote: allinriverking

Thank you everyone for the results, but I think I relayed question wrong. Going with Bruce's example, I would like to know what the odds of drawing those letters A through I before either of the letters X, Y or Z are drawn, not all three X, Y and Z drawn. 1 in 220 seems about right, maybe I'm missing what Bruce is saying. Thanks again.

It's the same answer. Even though you stop once you draw X, Y, or Z, you could keep drawing until you get all 12 as that won't change the result. Then you consider it a win if you get all of A-I before any of the X-Z. That way you can consider all 12! = 12*11*10*...*1 possible sequences which are equally likely. Note that gives the same answer as sallymustang and ThatDonGuy, but they don't have to consider drawing all 12. They are saying that the probability is 9/12 that you get one of A-I before any X-Z. Then once you do that, it's 8/11 that you get a second different A-I before any X-Z, then 7/10 for the 3rd, etc. So

9/12 * 8/11 * 7/10 * ... * 1/4 = (9*8*7*...*1)/(12*11*10*...*4)

= 9!/(12!/3!) = 9!3!/12!

= 1/220.

Understand now thanks