Thread Rating:
I am working currently on side bets for the game 30 and 40 (known mainly in Europe) explained on this page :
I was wondering how can I calculate the probability of number of cards dealt with a 6 decks shoe for whether the black or red hand .
Example : what are the chances that the black hand got 6 cards dealt to land between 30 and 40 (30 is excluded by the way).
Your help will be really priceless
Thank you in advance
In your case if you only want to know how many cards are used, then you only need to deal one hand, since by symmetry the result applies to either. This can be achieved by looking at all ways to get 31-40 where the last card takes you over 30. (Note obviously the two results are correlated, so this only gives the chances of one hand, not both.)
If you want to analyse the "insurance" part, then you need to run both hands and see how often each outcome occurs. This would be slightly harder (or just longer to run) than the first.
btw I've only ever seen the game in Monte Carlo (for chip collectors it was the only way to get a One Euro Chip) so I'm slightly surprised you're worrying about it.
As has been said, you're marginally better off taking insurance - this can be worked out intuitively by saying that the chances of 31 is the highest (p21*p(10)+p22*p(9)....+p30*p(A), while the chances of 40 is p30*p(10)), perhaps using an infinite deck to make a quick approximation.
You are exactly right, there are 2 different ways to calculate it.
First which is the easiest one is with a simulator but unfortunately I don't have it in my possession and that was the method use by Wizard of odds.
The second one is with mathematic. But manually they are too many different combinations that are possible and it will be mainly impossible. I am sure that they are formula that can help and that I am not aware of.
The goal is to predict how many cards will be dealt only for the black hand or red hand but not for both in the same round.
The idea is to offer a side bet where the player can bet on boxes on the exact number of cards dealt on the black hand.
This game is present in Europe in Monte-carlo and Italy as well and is similar to Baccara.
In order to be qualified the hand has to be between 31 and 40 included. By the way Ace value is one, and faces value is 10.
With a 6 decks shoe, there is at least 4 cards that have to be drawn to be qualified (3 cards with a 10 value and any card) and maximum 28 cards can be drawn (24 aces and 4 cards of "2")
The question if I try to clear-up my previous posts will be : what are the probabilities of getting a hand qualified with 4 cards drawn ? with 5 cards drawn ? etc. up to 28 cards drawn. The total result of all probabilities have to be 1 obviously.
Or perhaps someone have a preset simulator of a 6 decks shoe that I can use in Excel for instance ?
Thanks in advance
Technically it's quite an easy puzzle to solve, just work through all the combinations of cards, and add up the permutations/probabilities. You will need to do some programming of sorts - whether it's an excel spreadsheet or an actual program. (An excel spreadsheet for s17 blackjack has 54k lines, so more would be needed for this because Aces=1.)Quote: floomc...But manually they are too many different combinations that are possible and it will be mainly impossible. I am sure that they are formula that can help and that I am not aware of....
fwiw the best way is to use infinite deck to get an approximation and then see how the results change for the number of decks needed (as this is harder to iron out the errors).
I suspect a few people on this forum have a tested simulator, but like me, they've probably taken quite a while to build it and aren't really going to give it away for free.
I have personally played the game in Monte Carlo, so do understand how it works. As you say the key factor to remember is that Aces=1.
cards = 4 prob = 0.260817
cards = 5 prob = 0.36705
cards = 6 prob = 0.239624
cards = 7 prob = 0.0968788
cards = 8 prob = 0.0280436
cards = 9 prob = 0.00626816
cards = 10 prob = 0.00112778
cards = 11 prob = 0.000167254
cards = 12 prob = 2.07288e-05
cards = 13 prob = 2.16219e-06
cards = 14 prob = 1.90061e-07
cards = 15 prob = 1.40235e-08
R is a free download which you can have working in a few minutes. Computing these 15 takes a few minutes. Doing all 28 could take 18 hours depending on the speed of your machine, but as you can see, the probabilities become very small, so you probably don't care about all of those. EDIT: You might run out of RAM before you can do all 28. I could only go up to 20, but I only have 2 GB of RAM on XP and made no attempt to increase the memory allocation for R. 28 should require about 14 GB, so your mileage may vary. Let me know if you manage to do all 28. EDIT2: You will also run out of precision before you get to 28. At 17 I've observed fewer than 6 significant digits due to finite precision roundoff error, and beyond 20 was not useable as it just produces 0. At 20 there should be almost 3 significant digits of precision.
EDIT3: See much better program later in thread which can do all 28 in 10 seconds with no roundoff problems.
### Exact P(31-40 in k cards drawn from 6 deck shoe)
require(compiler)
enableJIT(3)
max.cards = 28
p = rep(0,28)
for (k in 4:max.cards) {
m = combn(10+k-1,k) # hands with k cards -> columns of m in * and | form
hands.tot = 0
hands.gt.30 = 0
for (j in 1:choose(10+k-1,k) ) { # for each hand
cards = rle(cumsum(c(m[1,j],diff(m[,j]) - 1))) # convert cards to run length form
total = sum(cards$values * cards$lengths) # sum of cards
hands = 1
if ( any(cards$values < 10) )
hands = hands*prod(choose(24,cards$lengths[cards$values < 10]))
if ( any(cards$values == 10) )
hands = hands*choose(96,cards$lengths[cards$values == 10])
if (total > 30) hands.gt.30 = hands.gt.30 + hands
hands.tot = hands.tot + hands
}
p[k] = hands.gt.30/hands.tot - sum(p[3:(k-1)])
cat('\ncards =',k, ' prob =',p[k])
flush.console()
remove(m)
}
Doing this calculation in a way that would not require an excessive amount of time, storage, or complicated code made for an interesting programming exercise.
The exact calculation proceeds by first enumerating every possible combination of ranks for a number of cards k where k goes from 4 to 28. This is done by considering the number of distinguishable ways to place k indistinguishable balls into 10 numbered cups which is C(k+10-1,k) by Bose-Einstein. This result can be seen by representing the balls by stars (*) and the cups by bars (|) which form the partitions. For example, the hand 1,2,2,2,5,10,10 would be represented by
|* |*** | | |*| | | | |** |
There are k stars and 11 bars, but since the first and last are always bars, we want to order k + 9 stars and bars, so there are C(k+9,k) ways to place the stars. In general, there are C(k+c-1,k) distinguishable ways to place k indistinguishable balls into c numbered cups.
The program initially represents each hand type in a form that records the position of each star. This is done for every possible combination of k cards regardless of whether the total is < 30, 31-40, or > 40. Each of these is then converted to a form that records the rank and number of each rank with the rle function (run length encoding). From this we can compute the number of combinations of each hand since there are C(24,r) ways to have r ranks of a number from 0-9, and C(96,r) ways to have r ranks of 10. We then count the number which have a total > 30, and also the total number, and we use these to compute the probability that the total is > 30. Note that this probability includes totals > 40 at this point, but we want the probability of 31-40.
Now notice that certain combinations are only possible in certain orders. For example, with the above hand 1,2,2,2,5,10,10 the 1 cannot come last or we would already have 31. In order to avoid worrying about permutations, we simply subtract from the probability of > 30 the sum of the probabilities that we have computed previously for 31-40. Of course when k=4 this will just be 0 since the probabilities are 0 for k=1 to 3. This will then give the new probability for a total of 31-40 since we have the probability of being greater than 30 minus the probability that we already had >30 with fewer cards. All the totals over 40 must have been over 30 with one fewer card, so those will all be subtracted.
That gives the exact probabilities taking into account card removal. Here is the simulation which verifies it.
### Simulation of P(31-40 in k cards drawn from 6 deck shoe)
require(compiler)
enableJIT(3)
shoe = c(rep(1:9,24), rep(10,96))
count = rep(0,28)
sims = 0
while(1) {
cards = sample(shoe,28,replace=FALSE)
num = which(cumsum(cards) > 30)[1]
count[num] = count[num] + 1
sims = sims + 1
}
p = count/sims
error = 3.29*sqrt(p*(1-p)/sims)
p
error
sims
> p
[1] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[4] 2.60791501030337e-01 3.67049132155802e-01 2.39654983345883e-01
[7] 9.68804993899163e-02 2.80389918291986e-02 6.26976778258475e-03
[10] 1.12444660437660e-03 1.67739909231004e-04 2.07170207833965e-05
[13] 2.03527038808816e-06 1.85661498397027e-07 3.50304713956654e-09
[16] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[19] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[22] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[25] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[28] 0.00000000000000e+00
> error
[1] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[4] 8.54966467112050e-05 9.38568532201649e-05 8.31222848852157e-05
[7] 5.75983023271459e-05 3.21458198978056e-05 1.53701769701255e-05
[10] 6.52595386914477e-06 2.52174206677936e-06 8.86294472748508e-07
[13] 2.77798248833397e-07 8.39034413370807e-08 1.15250250689876e-08
[16] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[19] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[22] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[25] 0.00000000000000e+00 0.00000000000000e+00 0.00000000000000e+00
[28] 0.00000000000000e+00
> sims
[1] 285465756
This runs until user breaks. The error shown gives approximately the 99.9% confidence interval, but this won't be accurate the larger numbers of cards since they happen too few times. Here 15 only happened 1 time in over 285 million games, and > 15 cards never happened. The user can restart the sim from the main while loop to continue where it left off to get more accurate numbers.
I also did an an infinite deck approximation which makes the draws independent by performing repeated convolutions of the probability mass function for a card with itself to get the probability mass function for the sum. This is accurate to about 0.1% up to 8 cards, and then the relative error increases as the probabilities get smaller for more cards. Here is that code and results which you can compare.
### Infinite deck approximation of P(31-40 in k cards drawn from 6 deck shoe)
conv = function(f,g) convolve(f,rev(g),type="o")
p = rep(0,28)
shoe = c(rep(24/312,9), 96/312)
pmf = conv(shoe,shoe)
pmf = conv(pmf,shoe)
for (k in 4:28) {
pmf = conv(pmf,shoe)
p[k] = sum(pmf[(31-k+1):length(pmf)]) - sum(p[3:(k-1)])
cat('\ncards =',k, ' prob =',p[k])
flush.console()
}
cards = 4 prob = 0.262105668569028
cards = 5 prob = 0.365194065064518
cards = 6 prob = 0.238220737551455
cards = 7 prob = 0.0973343003468911
cards = 8 prob = 0.0288831085963238
cards = 9 prob = 0.00673199389136303
cards = 10 prob = 0.00128892339250763
cards = 11 prob = 0.000208347655846985
cards = 12 prob = 2.89477981323394e-05
cards = 13 prob = 3.4988305867012e-06
cards = 14 prob = 3.70680356964748e-07
cards = 15 prob = 3.45629842524176e-08
cards = 16 prob = 2.84046064447097e-09
cards = 17 prob = 2.05674921538446e-10
cards = 18 prob = 1.31012978243916e-11
cards = 19 prob = 7.32192084740291e-13
cards = 20 prob = 3.56381590904675e-14
cards = 21 prob = 1.33226762955019e-15
cards = 22 prob = 1.55431223447522e-15
cards = 23 prob = -2.22044604925031e-16
cards = 24 prob = -2.22044604925031e-16
cards = 25 prob = -6.66133814775094e-16
cards = 26 prob = 0
cards = 27 prob = 0
cards = 28 prob = -1.11022302462516e-16
Note the small negative numbers are an artifact of the fast Fourier transform used to compute the convolution.
Quote: BruceZI wrote an R script to compute the exact probabilities for 4-28 cards for the 6 deck shoe. This takes into account card removal.
cards = 4 prob = 0.260817415415043
cards = 5 prob = 0.367049883058072
cards = 6 prob = 0.239624080265083
cards = 7 prob = 0.096878765177041
cards = 8 prob = 0.0280435733038619
cards = 9 prob = 0.0062681554164814
cards = 10 prob = 0.00112777788734808
cards = 11 prob = 0.000167253516744736
cards = 12 prob = 2.07287824863789e-05
cards = 13 prob = 2.16218639215171e-06
cards = 14 prob = 1.90061416938114e-07
cards = 15 prob = 1.40234509560244e-08
nice of course
thank you
lots to go over
just had to see what SN Ethier showed in his book
page 627
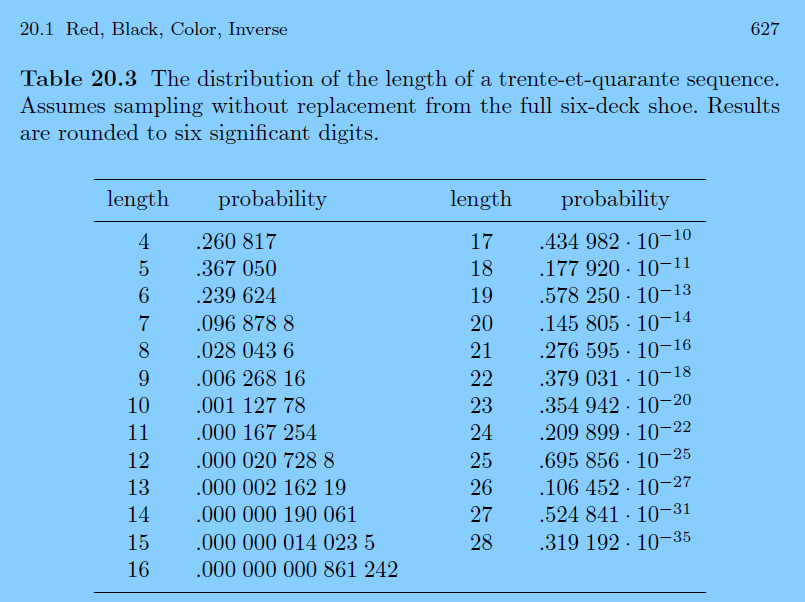
looks sweet as always
never played the game (love dice games more)
Quote: mustangsally
just had to see what SN Either showed in his book
page 627
looks sweet as always
never played the game (love dice games more)
We start to differ at 17. The digits are close, but his exponent looks off by 1. Note that from 16 to 17 his value changes by only about half which is less than the surrounding values.
cards = 16 prob = 8.6124174458746e-10
cards = 17 prob = 4.34983160602087e-11
cards = 18 prob = 1.77913239696181e-12
cards = 19 prob = 5.79536418854332e-14
cards = 20 prob = 1.4432899320127e-15
Does he say what method he uses? Perhaps it's a simulation with too many digits reported.
EDIT: This is due to finite precision roundoff error in my calculation.
Thank you so much for your help that is priceless.
Like I said, I was working on developing side bets on this game and I was stuck with these probabilities.
Your work is awesome with your clear explanation and demonstration (even though I don't grasp everything but that is due to my poor lvl in math and coding) !!
I won't manage to do the calculation for drawing >20 cards. Like you said, probabilities of occurrences are infinitely small and don't deserve to be calculated.
yesQuote: BruceZDoes he say what method he uses? Perhaps it's a simulation with too many digits reported.
a sim... that is not at all Stewart's style if you have looked thru his book
it is available
is this it? i have more to do today

Stewart N. Ethier
The Doctrine of Chances
Probabilistic Aspects of Gambling
there is lots of math in his chapter(s) too and i see not one simulation in this chapter 20
not that he did not do any, just not in the book
i fired up R in me win10 64bit i7 dell laptop 6GB RamQuote: BruceZWe start to differ at 17. The digits are close, but his exponent looks off by 1. Note that from 16 to 17 his value changes by only about half which is less than the surrounding values.
cards = 14 prob = 1.90061416938114e-07
cards = 15 prob = 1.40234509560244e-08
cards = 16 prob = 8.6124174458746e-10
cards = 17 prob = 4.34983160602087e-11
for a test drive
the first 11 went fast then the slow down
here is what i gots (just to 17)
cards = 4 prob = 0.260817415415043
cards = 5 prob = 0.367049883058072
cards = 6 prob = 0.239624080265083
cards = 7 prob = 0.096878765177041
cards = 8 prob = 0.0280435733038619
cards = 9 prob = 0.0062681554164814
cards = 10 prob = 0.00112777788734808
cards = 11 prob = 0.000167253516744736
cards = 12 prob = 2.07287824863789e-05
cards = 13 prob = 2.16218639215171e-06
cards = 14 prob = 1.90061416938114e-07
cards = 15 prob = 1.40234508450021e-08
cards = 16 prob = 8.61241855609762e-10
cards = 17 prob = 4.34983160602087e-11
looks like we start to differ at 15 and 16 only
you use XP... well
i wore out 2 of them machines...
there have been reports of typos in that DOC book
and i would bet $1
Prof. Ethier would like to know if any more are found
he seems real nice
but now breakfast and chores
So I'm the guy who showed too many digits, not your author. I still believe your author's exponents are too high by 1 starting at 17.
Quote: mustangsally
Stewart N. Ethier
The Doctrine of Chances
Probabilistic Aspects of Gambling.
I implemented this in R and optimized it so that you can now compute all 28 in under 10 seconds! This method doesn't have the roundoff problems that the previous one had since there are no subtractions. I changed the order of summation so that the part of the calculation that depends only on k1...k10 could be factored out of the sum over i and computed only once. I also used combinations instead of permutations so the multinomial factor isn't necessary. Each valid vector k1...k10 is used in the computation as soon as it is found for all values of i, so these never need to be stored as in a previous version of this code. So I'm computing:
As in the original, k is the sum of the first K-1 cards, n1..n9 = 24, and n10 = 96.
Note that the ni - ki is the number of ways to choose the last card, and we divide by K for the total number of ways to choose the last card. So we are computing combinations of the first K-1 cards times the ways to choose the last card in both numerator and denominator.
### Exact P(31-40 in k cards drawn from 6 deck shoe) after Either
require(compiler)
enableJIT(3)
n = c(rep(24,9),96) # number of each card
Q = rep(0,28) # holds final probabilities
for (K in 4:28) { # for each possible number of cards K
for (k in 21:30) { # for each sum of first K-1 cards k
for (k10 in 0:3) {
k.v = k10
for (k9 in 0:max(0,min((k-10*k10)%/%9,K-1-k10))) {
k.v = c(k9,k.v)
for (k8 in 0:max(0,min((k-sum((9:10)*k.v))%/%8, K-1-sum(k.v)))) {
k.v = c(k8,k.v)
for (k7 in 0:max(0,min((k-sum((8:10)*k.v))%/%7, K-1-sum(k.v)))) {
k.v = c(k7,k.v)
for (k6 in 0:max(0,min((k-sum((7:10)*k.v))%/%6, K-1-sum(k.v)))) {
k.v = c(k6,k.v)
for (k5 in 0:max(0,min((k-sum((6:10)*k.v))%/%5, K-1-sum(k.v)))) {
k.v = c(k5,k.v)
for (k4 in 0:max(0,min((k-sum((5:10)*k.v))%/%4, K-1-sum(k.v)))) {
k.v = c(k4,k.v)
for (k3 in 0:max(0,min((k-sum((4:10)*k.v))%/%3, K-1-sum(k.v)))) {
k.v = c(k3,k.v)
for (k2 in 0:max(0,min((k-sum((3:10)*k.v))%/%2, K-1-sum(k.v)))) {
k.v = c(k2,k.v)
k1 = K-1-sum(k.v)
k.v = c(k1,k.v)
if ( sum(k.v) + 1 == K & sum(k.v*(1:10)) == k ) {
Q[K] = Q[K] + prod(choose(24,k.v[1:9]))*choose(96,k.v[10])*
sum(n[(31-k):10]-k.v[(31-k):10]) / (choose(312,K)*K)
}
k.v = k.v[-(1:2)] # Removes k1 and k2
}
k.v = k.v[-1] # Removes k3
}
k.v = k.v[-1] # Removes k4
}
k.v = k.v[-1] # Removes k5
}
k.v = k.v[-1] # Removes k6
}
k.v = k.v[-1] # Removes k7
}
k.v = k.v[-1] # Removes k8
}
k.v = k.v[-1] # Removes k9
}
k.v = k.v[-1] # Removes k10
}
}
cat('\ncards =',K,' prob =',Q[K])
flush.console()
}
Output:
cards = 4 prob = 0.260817
cards = 5 prob = 0.36705
cards = 6 prob = 0.239624
cards = 7 prob = 0.0968788
cards = 8 prob = 0.0280436
cards = 9 prob = 0.00626816
cards = 10 prob = 0.00112778
cards = 11 prob = 0.000167254
cards = 12 prob = 2.07288e-05
cards = 13 prob = 2.16219e-06
cards = 14 prob = 1.90061e-07
cards = 15 prob = 1.40235e-08
cards = 16 prob = 8.61242e-10
cards = 17 prob = 4.34982e-11
cards = 18 prob = 1.7792e-12
cards = 19 prob = 5.7825e-14
cards = 20 prob = 1.45805e-15
cards = 21 prob = 2.76595e-17
cards = 22 prob = 3.79031e-19
cards = 23 prob = 3.54942e-21
cards = 24 prob = 2.09899e-23
cards = 25 prob = 6.95856e-26
cards = 26 prob = 1.06452e-28
cards = 27 prob = 5.24841e-32
cards = 28 prob = 3.19192e-36
Quote: BruceZ[,,,I got the same numbers as he did except it verified that his powers of 10 for 17 and above are indeed all too large by one...
cards = 21 prob = 2.76595e-17
The reason the numbers are different is because of the terminology, you've put a significant digit before the decimal point (normalized) and Ethier hasn't (normal mantissa). Thus .276E-16 is the same as 2.76E-17.Quote: mustangsally
btw when I was brought up mainframe computers floating point numbers used this method keeping some bits for the exponent (and it's sign) and the rest for the fractional part (and it's sign), thus (unless all zeroes) the leading bit was always one and the value deemed to be between 1/2 and 1.
Quote: charliepatrickThe reason the numbers are different is because of the terminology, you've put a significant digit before the decimal point (normalized) and Ethier hasn't (normal mantissa). Thus .276E-16 is the same as 2.76E-17.
DOH! Didn't notice that. OK, so no problem.
Yahoo!Quote: BruceZI implemented this in R and optimized it so that you can now compute all 28 in under 10 seconds!
thank you
i wonder why OP wants just black (just red)
and not the total between black and red
that could be a side bet too
that is in "the book" 2
Hot HOT HOT in SoCal this weekend
not as hot as those Cubs!
Go Angels!
score more runs! (last nite was good)
Sally


