please remember that I am no a math or formula expert and therfore I am back with a question. thanks
please look here Example
this game is played with one die and after each throw the checker with the thrown number is moved one panel ahead. here the first throw was the number 1 and the checker was moved one panel ahead. the winner is the first who will end in the finish panel.
at start the chances to win is 5:1 and winner will end with 6
if you see this starting pic. what are now the chances for 1 or the others to cross the finish line first? actually chances will change after every move. what formula do I need to use to get always the right odds after each move till finish?
and what is the chance that until the end of the game the winner ended in finish and one of the other 5 checkers didn't move at all and is still sitting on the starting panel? that means that the number of the die was not thrown even once during the game.
Quote: sevenHi all
please remember that I am no a math or formula expert and therfore I am back with a question. thanks
please look here Example
this game is played with one die and after each throw the checker with the thrown number is moved one panel ahead. here the first throw was the number 1 and the checker was moved one panel ahead. the winner is the first who will end in the finish panel.
at start the chances to win is 5:1 and winner will end with 6
if you see this starting pic. what are now the chances for 1 or the others to cross the finish line first? actually chances will change after every move. what formula do I need to use to get always the right odds after each move till finish?
and what is the chance that until the end of the game the winner ended in finish and one of the other 5 checkers didn't move at all and is still sitting on the starting panel? that means that the number of the die was not thrown even once during the game.
This would be a fairly difficult homework problem�unless I�m overlooking a really simple way to do this (which I have a habit of doing).
I�ll keep the explanation at a minimal for now. I basically just used the negative binomial distribution to derive the following solution:
Let,
x = the number of spaces needed to win for the �checker� that you want to win
p,q,r,s,t = the number of spaces needed to win for each of the other checkers
Then, the probability for the checker you want to win is:

In your picture, the 1 checker needs 5 spaces while the rest each needs 6. So, plug in x=5 and plug in 6 for the rest of the variables. Compute to get 0.28298. So, the 1 checker now has a 28.3% chance to win. Therefore, the rest of the field has a 71.7% chance to win or 14.3% each.
Edit: Added an image of the expression and change the variables
Quote: PeeMcGeeQuote: sevenHi all
please remember that I am no a math or formula expert and therfore I am back with a question. thanks
please look here Example
this game is played with one die and after each throw the checker with the thrown number is moved one panel ahead. here the first throw was the number 1 and the checker was moved one panel ahead. the winner is the first who will end in the finish panel.
at start the chances to win is 5:1 and winner will end with 6
if you see this starting pic. what are now the chances for 1 or the others to cross the finish line first? actually chances will change after every move. what formula do I need to use to get always the right odds after each move till finish?
and what is the chance that until the end of the game the winner ended in finish and one of the other 5 checkers didn't move at all and is still sitting on the starting panel? that means that the number of the die was not thrown even once during the game.
This would be a fairly difficult homework problem�unless I�m overlooking a really simple way to do this (which I have a habit of doing).
I�ll keep the explanation at a minimal for now. I basically just used the negative binomial distribution to derive the following solution:
Let,
x = the number of spaces needed to win for the �checker� that you want to win
a,b,c,d,e = the number of spaces needed to win for each of the other checkers
Then, the probability for the checker you want to win is:
Summation {from a=0 to x=(a-1)}
Summation {from b=0 to x=(b-1)}
Summation {from c=0 to x=(c-1)}
Summation {from d=0 to x=(d-1)}
Summation {from e=0 to x=(e-1)}
((a+b+c+d+e+x-1)! / (a!b!c!d!e!(x-1)!)) * (1/6)a+b+c+d+e+x
In your picture, the 1 checker needs 5 spaces while the rest each needs 6. So, plug in x=5 and plug in 6 for the rest of the variables. Compute to get 0.28298. So, the 1 checker now has a 28.3% chance to win. Therefore, the rest of the field has a 71.7% chance to win or 14.3% each.
I don't know about the math, but I think these questions are germane:
Do you have to hit the goal exactly, or can you go over?
Do the players go in the same order each round? Does the game end when one checker reaches the goal, or do the others still have an opportunity?
Quote:
I don't know about the math, but I think these questions are germane:
Do you have to hit the goal exactly, or can you go over?
Do the players go in the same order each round? Does the game end when one checker reaches the goal, or do the others still have an opportunity?
My understanding of the game is there are no "players". You simply roll a six sided die and move the corresponding number one space towards the finish. As soon as one of the checkers reaches the final space the game is over.
Quote: AyecarumbaQuote: PeeMcGeeQuote: sevenHi all
please remember that I am no a math or formula expert and therfore I am back with a question. thanks
please look here Example
this game is played with one die and after each throw the checker with the thrown number is moved one panel ahead. here the first throw was the number 1 and the checker was moved one panel ahead. the winner is the first who will end in the finish panel.
at start the chances to win is 5:1 and winner will end with 6
if you see this starting pic. what are now the chances for 1 or the others to cross the finish line first? actually chances will change after every move. what formula do I need to use to get always the right odds after each move till finish?
and what is the chance that until the end of the game the winner ended in finish and one of the other 5 checkers didn't move at all and is still sitting on the starting panel? that means that the number of the die was not thrown even once during the game.
This would be a fairly difficult homework problem�unless I�m overlooking a really simple way to do this (which I have a habit of doing).
I�ll keep the explanation at a minimal for now. I basically just used the negative binomial distribution to derive the following solution:
Let,
x = the number of spaces needed to win for the �checker� that you want to win
a,b,c,d,e = the number of spaces needed to win for each of the other checkers
Then, the probability for the checker you want to win is:
Summation {from a=0 to x=(a-1)}
Summation {from b=0 to x=(b-1)}
Summation {from c=0 to x=(c-1)}
Summation {from d=0 to x=(d-1)}
Summation {from e=0 to x=(e-1)}
((a+b+c+d+e+x-1)! / (a!b!c!d!e!(x-1)!)) * (1/6)a+b+c+d+e+x
In your picture, the 1 checker needs 5 spaces while the rest each needs 6. So, plug in x=5 and plug in 6 for the rest of the variables. Compute to get 0.28298. So, the 1 checker now has a 28.3% chance to win. Therefore, the rest of the field has a 71.7% chance to win or 14.3% each.
I don't know about the math, but I think these questions are germane:
Do you have to hit the goal exactly, or can you go over?
Do the players go in the same order each round? Does the game end when one checker reaches the goal, or do the others still have an opportunity?
thank you for the question.
one can't go over because each one can only go one panel after each die throw. the die outcome tells the one with the number that came out to move
one panel ahead.
for example the die shows a 3 that means that number 3 will go one panel ahead. next throw is a six so number six goes one panel ahead.
game ends after one checker reaches the goal.
Quote: PeeMcGeeQuote:
I don't know about the math, but I think these questions are germane:
Do you have to hit the goal exactly, or can you go over?
Do the players go in the same order each round? Does the game end when one checker reaches the goal, or do the others still have an opportunity?
My understanding of the game is there are no "players". You simply roll a six sided die and move the corresponding number one space towards the finish. As soon as one of the checkers reaches the final space the game is over.
there could be 1 player and there could be 100 players. the idea is that at the start of the game each player could chose one or more from 1-6 that he thinks will end the winner.
but after each throw and move of a checker the chances are changing and players could bet again with different odds. that was the reason I posted my question for a formula to offer the right odds.
Quote: sevenQuote: PeeMcGeeQuote:
I don't know about the math, but I think these questions are germane:
Do you have to hit the goal exactly, or can you go over?
Do the players go in the same order each round? Does the game end when one checker reaches the goal, or do the others still have an opportunity?
My understanding of the game is there are no "players". You simply roll a six sided die and move the corresponding number one space towards the finish. As soon as one of the checkers reaches the final space the game is over.
there could be 1 player and there could be 100 players. the idea is that at the start of the game each player could chose one or more from 1-6 that he thinks will end the winner.
but after each throw and move of a checker the chances are changing and players could bet again with different odds. that was the reason I posted my question for a formula to offer the right odds.
That was my understanding. The expression I gave in my post will provide what you are seeking.
Quote: PeeMcGeeQuote: sevenQuote: PeeMcGeeQuote:
I don't know about the math, but I think these questions are germane:
Do you have to hit the goal exactly, or can you go over?
Do the players go in the same order each round? Does the game end when one checker reaches the goal, or do the others still have an opportunity?
My understanding of the game is there are no "players". You simply roll a six sided die and move the corresponding number one space towards the finish. As soon as one of the checkers reaches the final space the game is over.
there could be 1 player and there could be 100 players. the idea is that at the start of the game each player could chose one or more from 1-6 that he thinks will end the winner.
but after each throw and move of a checker the chances are changing and players could bet again with different odds. that was the reason I posted my question for a formula to offer the right odds.
That was my understanding. The expression I gave in my post will provide what you are seeking.
thank You very much for the solution very much appreciated. though I need to take my time to learn it now :)
Quote: PeeMcGee
I�ll keep the explanation at a minimal for now. I basically just used the negative binomial distribution to derive the following solution:
Let,
x = the number of spaces needed to win for the �checker� that you want to win
a,b,c,d,e = the number of spaces needed to win for each of the other checkers
Then, the probability for the checker you want to win is:
Summation {from a=0 to x=(a-1)}
Summation {from b=0 to x=(b-1)}
Summation {from c=0 to x=(c-1)}
Summation {from d=0 to x=(d-1)}
Summation {from e=0 to x=(e-1)}
((a+b+c+d+e+x-1)! / (a!b!c!d!e!(x-1)!)) * (1/6)a+b+c+d+e+x
In your picture, the 1 checker needs 5 spaces while the rest each needs 6. So, plug in x=5 and plug in 6 for the rest of the variables. Compute to get 0.28298. So, the 1 checker now has a 28.3% chance to win. Therefore, the rest of the field has a 71.7% chance to win or 14.3% each.
I'm not familiar with the negative binomial distribution, so I'm trying to learn. When I plug x=5 and a=b=c=d=e=6 into the equation
((a+b+c+d+e+x-1)! / (a!b!c!d!e!(x-1)!)) * (1/6)a+b+c+d+e+x I calculate:
(34!/(6!5*4!)) * (1/6)35 = 0.000739651.
Now, what are the values of those 5 summation terms and how do I apply them to arrive at an answer of 0.28198?
no wayQuote: DJTeddyBearThis smells like homework.
looks like another game idea from seven
ok
so the checkers move one square to the right depending on the # that is rolled.
say the 1st roll = 1 (OP example)
so checker is now at square1 (one die roll)
the others still at 0
say we speed this up and roll 2 dice
next roll = 3,1
checker moves 1 space to right and is now at square 2
c2 is still at space 0
c3 now moves one space to the right and is at aquare 1
c4,c5 and c6 are just watching at square 0
next roll = 1,1
c1 moves 2 squares to the right and is now at 4
the others are where they were the last roll
1st to square #6 is the winner
lots of states this game can be in
and i love dice games
so i would solve this for each step with a Markov chain
also looks like no winner on the first 5 rolls of 1 die
and there has to be a winner on the 31st roll (6*5, all checkers at 5 and still having the same chance to be the winner as B4 the game started)
OP
is this your game idea and do I have the rules correct?
the number on the die moves that checker# one space or square to the right
next roll
Sally
Quote: mustangsallyno way
looks like another game idea from seven
ok
so the checkers move one square to the right depending on the # that is rolled.
say the 1st roll = 1 (OP example)
so checker is now at square1 (one die roll)
the others still at 0
say we speed this up and roll 2 dice
next roll = 3,1
checker moves 1 space to right and is now at square 2
c2 is still at space 0
c3 now moves one space to the right and is at aquare 1
c4,c5 and c6 are just watching at square 0
next roll = 1,1
c1 moves 2 squares to the right and is now at 4
the others are where they were the last roll
1st to square #6 is the winner
lots of states this game can be in
and i love dice games
so i would solve this for each step with a Markov chain
also looks like no winner on the first 5 rolls of 1 die
and there has to be a winner on the 31st roll (6*5, all checkers at 5 and still having the same chance to be the winner as B4 the game started)
OP
is this your game idea and do I have the rules correct?
the number on the die moves that checker# one space or square to the right
next roll
Sally
hi Sally
You are absolutely spot on :) but could you please ELI5
-lots of states this game can be in
and i love dice games
so i would solve this for each step with a Markov chain-
yes it is my game idea but who knows maybe somewhere out there was or is some one with the same idea
thanks for posting
Quote: gordonm888Quote: PeeMcGee
I�ll keep the explanation at a minimal for now. I basically just used the negative binomial distribution to derive the following solution:
Let,
x = the number of spaces needed to win for the �checker� that you want to win
p,q,r,s,t = the number of spaces needed to win for each of the other checkers
Then, the probability for the checker you want to win is:
Summation {from a=0 to x=(a-1)}
Summation {from b=0 to x=(b-1)}
Summation {from c=0 to x=(c-1)}
Summation {from d=0 to x=(d-1)}
Summation {from e=0 to x=(e-1)}
((a+b+c+d+e+x-1)! / (a!b!c!d!e!(x-1)!)) * (1/6)a+b+c+d+e+x
In your picture, the 1 checker needs 5 spaces while the rest each needs 6. So, plug in x=5 and plug in 6 for the rest of the variables. Compute to get 0.28298. So, the 1 checker now has a 28.3% chance to win. Therefore, the rest of the field has a 71.7% chance to win or 14.3% each.
I'm not familiar with the negative binomial distribution, so I'm trying to learn. When I plug x=5 and a=b=c=d=e=6 into the equation
((a+b+c+d+e+x-1)! / (a!b!c!d!e!(x-1)!)) * (1/6)a+b+c+d+e+x I calculate:
(34!/(6!5*4!)) * (1/6)35 = 0.000739651.
Now, what are the values of those 5 summation terms and how do I apply them to arrive at an answer of 0.28198?
My apologies, I wasn�t sure how to make the expression clear on the forums. Hopefully, this helps�

It�s very computational�you�ll want a program that can solve summations.
HiQuote: sevenhi Sally
ok, i try, i am not a very good teacherQuote: seven<snip>but could you please ELI5
lots of states this game can be in
kind of like water
it can be in 3 "states"
liquid, solid or a gas
so your game as it unfolds can be in different states after each roll
depending on the # of successes for each number rolled (your checkers)
1 thru 6 inclusive
after the 1st roll
we could be in 1 of 6 states
1.1 (checker 1 with 1 success or hit) 2.0, 3.0, 4.0, 5.0, 6.0 (all other checkers at 0 hits)
or
1.0, 2.1, 3.0, 4.0, 5.0, 6.0
or
1.0, 2.0, 3.1, 4.0, 5.0, 6.0
and on for 1 each
now from that first roll
each state can move to other states and there will be more of them (states)
like
1.0, 2.1, 3.0, 4.0, 5.0, 6.0
could move to
1.0, 2.2, 3.0, 4.0, 5.0, 6.0 with a probability = 1/6
or
1.1, 2.1, 3.0, 4.0, 5.0, 6.0
or
1.0, 2.1, 3.1, 4.0, 5.0, 6.0
and so one
it becomes a fun exercise on finding all the combinations that all states can be in (always a trick)
after each roll
this is how i would do this
other than a simulation
i get also 28.3% for OP example for c1 to win
and with the first 2 rolls being two different faces (say 1 and 2) i gets 25.2% for 1 or 2 and 12.4% for the others
and
with the 1st 2 rolls being the same (say 1,1)
not a certain winner for 1, btw
abouts 44.4% vs 11.1%
but you said you want to know the probability of winning for each checker
after each roll and that is exactly what a Markov chain method can do for you (and me too)
this one looks fun
once all the states and the transition probabilities are entered into the matrix, just simple matrix multiplication returs lots of answers
lots of them
even for the absorbing states (1.6 or 2.6 and so on)
no lesson on that part here
"and i love dice games" i do
"so i would solve this for each step with a Markov chain" yes i would do just that if I find the time
so this game is just a RACE
could have 1st and 2nd place prizes too
it could be even a party game using people instead of checkers
lots of "states" this game can be in ;)
Sally
Quote: mustangsallyHi
ok, i try, i am not a very good teacher
lots of states this game can be in
kind of like water
it can be in 3 "states"
liquid, solid or a gas
so your game as it unfolds can be in different states after each roll
depending on the # of successes for each number rolled (your checkers)
1 thru 6 inclusive
after the 1st roll
we could be in 1 of 6 states
1.1 (checker 1 with 1 success or hit) 2.0, 3.0, 4.0, 5.0, 6.0 (all other checkers at 0 hits)
or
1.0, 2.1, 3.0, 4.0, 5.0, 6.0
or
1.0, 2.0, 3.1, 4.0, 5.0, 6.0
and on for 1 each
now from that first roll
each state can move to other states and there will be more of them (states)
like
1.0, 2.1, 3.0, 4.0, 5.0, 6.0
could move to
1.0, 2.2, 3.0, 4.0, 5.0, 6.0 with a probability = 1/6
or
1.1, 2.1, 3.0, 4.0, 5.0, 6.0
or
1.0, 2.1, 3.1, 4.0, 5.0, 6.0
and so one
it becomes a fun exercise on finding all the combinations that all states can be in (always a trick)
after each roll
this is how i would do this
other than a simulation
but you said you want to know the probability of winning for each checker
after each roll and that is exactly what a Markov chain method can do for you (and me too)
this one looks fun
once all the states and the transition probabilities are entered into the matrix, just simple matrix multiplication returs lots of answers
lots of them
even for the absorbing states (1.6 or 2.6 and so on)
no lesson on that part here
"and i love dice games" i do
"so i would solve this for each step with a Markov chain" yes i would do just that if I find the time
so this game is just a RACE
could have 1st and 2nd place prizes too
it could be even a party game using people instead of checkers
lots of "states" this game can be in ;)
Sally
thanks for the patience and explanation very much appreciated. I will later talk to google about Markov :)
yes the game is a race idea. it could be horses, cars, people etc. but I thought it would be boring if there would be bets at the start and then
just to wait who will be first to cross the finish line. IMO it would be much more interesting to give new quotes/odds after each move.
Quote: PeeMcGeeMy apologies, I wasn�t sure how to make the expression clear on the forums. Hopefully, this helps�
It�s very computational�you�ll want a program that can solve summations.
Question: each summation is for a variable from 0 to "that particular variable - 1" (e.g the first summation is the sum over all values of a from 0 to "a-1"). Are the variables a,b,c,d,e as the summation variables different from the a,b,c,d,e "target" values, in which case, you should change one of those sets of variables to, say, p,q,r,s,t?
I understand that the fraction is the number of permutations of (a + b + c + d + e + (x-1)) items where a are one value, b are another, c are a third, d are a fourth, e are a fifth, and the remaining (x-1) are a sixth.
Quote: PeeMcGee
My apologies, I wasn�t sure how to make the expression clear on the forums. Hopefully, this helps�
It�s very computational�you�ll want a program that can solve summations.
Wow. I agree that the equation is probably too complicated for Excel. Do you use Mathematica? or what computational software do you use, or would you recommend?
I have always struggled with exactly this kind of problem - a sequence of trials with multiple discrete random outcomes - and I am grateful to you for pointing out the negative binominial distribution, which I was unaware of. It is exciting to discover new tricks to learn.
By the way, in your summations it is a little unconventional for a parameter such as "a" to be defined as ranging from 0 to "a-1" - but I do understand exactly what you mean, lol -and I thank you for the effort to post the equation in a format that is so clear.
Quote:Question: each summation is for a variable from 0 to "that particular variable - 1" (e.g the first summation is the sum over all values of a from 0 to "a-1"). Are the variables a,b,c,d,e as the summation variables different from the a,b,c,d,e "target" values, in which case, you should change one of those sets of variables to, say, p,q,r,s,t?
Quote:By the way, in your summations it is a little unconventional for a parameter such as "a" to be defined as ranging from 0 to "a-1" - but I do understand exactly what you mean, lol -and I thank you for the effort to post the equation in a format that is so clear.
Ha, yea nice catch guys. When I was creating the image, I did realized that I was using the variables twice. I was going to change them to a different set, but wasn�t sure if that would had caused more confusion (my original post and image has been corrected). Thanks for bringing it up.
But yea�just know that the upper limit on each summation is the number of spaces needed for that checker. So for example, if all the checkers are at the start, every summation will be from 0 to 6. Which means you have 65 iterations to do.
Quote:Wow. I agree that the equation is probably too complicated for Excel. Do you use Mathematica? or what computational software do you use, or would you recommend?
I wrote a program in Python that solves it.
Excel could do it, but it would require a lot of work on the user. There might be some creative way to do it easy though.
Also, WolframAlpha might be an option.
Quote:I understand that the fraction is the number of permutations of (a + b + c + d + e + (x-1)) items where a are one value, b are another, c are a third, d are a fourth, e are a fifth, and the remaining (x-1) are a sixth.
The idea is that in order for the �x-checker� to win it must have been the last checker to move and no other checker moved the number of spaces they needed to reach the finish (hence the minus one in the upper limits).
So for example if every checker is at the start then each checker can move 0 to 5 spaces. The number of combinations that each checker can move is the fraction part. The probability in which that particular combination occurs is (1/6)total number of rolls.
So let�s say each of the six checkers moved exactly 5 spaces. That would be 30 dice rolls. There are 30!/(5!)6 ways to move six checkers exactly 5 spaces each. Each combination has a (1/6)30 chance of happening. Then there�s one last roll that must be the x-checker. So then you multiply by another 1/6.
Again, that would be for each checker to move exactly 5 spaces. But checker b, for example, might only move 2 spaces or zero or whatever. So then that�s why you have five summations.
i agree with youQuote: seventhanks for the patience and explanation very much appreciated. I will later talk to google about Markov :)
yes the game is a race idea. it could be horses, cars, people etc. but I thought it would be boring if there would be bets at the start and then
just to wait who will be first to cross the finish line. IMO it would be much more interesting to give new quotes/odds after each move.
i played a simple version by meself (a 2 hit version)
after i set up a 70x70 transition matrix in Excel of course
it was a blast and i showed it to me hubby B4 dinner and he said
this is fun
where did you find this game?
I mean, i have the per roll bets worked out, game will end on the 7th roll at the latest
the probability distribution
and something like this showing if one starts with some hits the ending distribution
this is what i really like about a Markov chain
and Excel loves these too
really simple math once you know how it is done , just as the other poster with the super sum formula
showed, once one knows how...
==============================
i think the number of states for the 6 hit version will be very large but i have not gone there
or thought more about it
=============================
this is fun to play, in my opinion
and many in-round bets can be easily made once the probabilities are worked out
ok
the Angles won and it was an under
so i won again and again
i am so lucky
Sally
thank you for sharing!
Quote: PeeMcGee
I wrote a program in Python that solves it.
Excel could do it, but it would require a lot of work on the user. There might be some creative way to do it easy though.
Also, WolframAlpha might be an option.
thanks for all the help to solve the problem. what is your opinion regarding Sally's idea to solve it with Markov? and lets say I want to bring this idea online
and I want to give the users after each move of a checker the the right odds so each user can bet on the winner at any time of the game as long no checker crossed the winner line . what program should I use? I understood Excel would not be good or not work. would the python program that you did solve this problem?
Quote: mustangsallyi agree with you
i played a simple version by meself (a 2 hit version)
after i set up a 70x70 transition matrix in Excel of course
it was a blast and i showed it to me hubby B4 dinner and he said
this is fun
where did you find this game?
the Angles won and it was an under
so i won again and again
i am so lucky
Sally
thank you for sharing!
what is advantage of the 2 hit version? tbecause it ends a bit quicker what would maybe good for testing?
glad that you guys had fun with the game :)
i found the 6 hit version too boring as it takes too many rolls to find a winner (19.7 simulated)Quote: sevenwhat is advantage of the 2 hit version?
of course, more dice each roll can help that.
and
the 1 hit version was not a challenge as it ended too fast (1 roll)
too this or too that
the 2 hit version 4 me was easy to do the math in Excel
but the 3 hit version looks to be more challenging (at least I do have a list of all the states, 3903 of them)
i could change the number of states for each hit version for a Markov chain
MAYbe just 0.6,1.5,2.4,3.3 etc (hits.miss) but as you see the math gets real crazy for all the possible permutations that there can be, even for combinations too
i have to look at this again later too
i also like playing the 3 hit version at 7.3 rolls per game (simulated)
(the 4 and 5 do not sound interesting but i have not tried them)
so i am certain i will do-the-math on it (or at least attempt it)
sure, the 2hit ends much quicker than the 6hit versionQuote: seventbecause it ends a bit quicker what would maybe good for testing?
and one can still have in-round betting chances too, i can see
here is the mean number of rolls for the 2 hit version: 3.774691358
that is from this distribution that the game ends on Roll X (max rolls for a winner =7)
1: 0
2: 0.166666667
3: 0.277777778
4: 0.277777778
5: 0.185185185
6: 0.077160494
7: 0.015432099
these can be found by hand if one wants too
ok
long weekend coming up
next week WSOP in Las Vegas starts
have fun!
thank you again for the game idea!
Sally
Quote: seventhanks for all the help to solve the problem. what is your opinion regarding Sally's idea to solve it with Markov? and lets say I want to bring this idea online
and I want to give the users after each move of a checker the the right odds so each user can bet on the winner at any time of the game as long no checker crossed the winner line . what program should I use? I understood Excel would not be good or not work. would the python program that you did solve this problem?
Markov is a valid way to solve it. It�s just that there are so many states. I found a way to maybe reduce it down to like 400 or so states�but that�s still quite a bit.
Yes, Python can do what you are seeking. Do you know Python? Anyways, here is my program:
import math
x = 6
p = 6
q = 6
r = 6
s = 6
t = 6
total = 0
for a in range(p):
for b in range(q):
for c in range(r):
for d in range(s):
for e in range(t):
total += (math.factorial(a+b+c+d+e+x-1) / (math.factorial(a) * math.factorial(b) * math.factorial(c) * math.factorial(d) * math.factorial(e) * math.factorial(x-1)) * ((1/6)**(a+b+c+d+e+x)))
print(total)
The x,p,q,r,s,t are all the variables I discussed in my original post. So when one of the checkers moves, you can have the program reduce the corresponding variable by one and then calculate the new probability.
Quote: PeeMcGeeMarkov is a valid way to solve it. It�s just that there are so many states. I found a way to maybe reduce it down to like 400 or so states�but that�s still quite a bit.
Yes, Python can do what you are seeking. Do you know Python? Anyways, here is my program:
import math
x = 6
p = 6
q = 6
r = 6
s = 6
t = 6
total = 0
for a in range(p):
for b in range(q):
for c in range(r):
for d in range(s):
for e in range(t):
total += (math.factorial(a+b+c+d+e+x-1) / (math.factorial(a) * math.factorial(b) * math.factorial(c) * math.factorial(d) * math.factorial(e) * math.factorial(x-1)) * ((1/6)**(a+b+c+d+e+x)))
print(total)
The x,p,q,r,s,t are all the variables I discussed in my original post. So when one of the checkers moves, you can have the program reduce the corresponding variable by one and then calculate the new probability.
thank you for providing the python program. to be frank I have no coding experience. I will look for a coder to code the game with a nice design. like horse trotters race, regular horse, cars, motorcycle etc so each user can choose the race he likes.
could the coder implement your python program so it will show next to the checker (horse etc ) the new odds so they can bet on it?
that sounds wonderfulQuote: sevenI will look for a coder to code the game with a nice design. like horse trotters race, regular horse, cars, motorcycle etc so each user can choose the race he likes.
a good one could easily do thatQuote: sevencould the coder implement your python program so it will show next to the checker (horse etc ) the new odds so they can bet on it?
but for the game of 6hits for example
you would probably not want each roll to offer a new bet
MAYbe every so many rolls a new bet(s) a futures bet so to speak
and the prorgram would already have the odds to offer for each bet in a table
not calculating every time
like after 3 rolls say 1,2,3 rolled, in any order (3 single hits)
prob for 1,2 or 3 to win = abouts 22.5% each
4,5,and 6 now at = abouts 10.8% each
odds can easily come from that
is this a
for fun play money game
or
for a house edge real money game to offer?
in other words
what are you after?
(other than fame or fortune)
Sally
Quote: mustangsallythat sounds wonderful
a good one could easily do that
but for the game of 6hits for example
you would probably not want each roll to offer a new bet
MAYbe every so many rolls a new bet(s) a futures bet so to speak
and the prorgram would already have the odds to offer for each bet in a table
not calculating every time
like after 3 rolls say 1,2,3 rolled, in any order (3 single hits)
prob for 1,2 or 3 to win = abouts 22.5% each
4,5,and 6 now at = abouts 10.8% each
odds can easily come from that
is this a
for fun play money game
or
for a house edge real money game to offer?
in other words
what are you after?
(other than fame or fortune)
Sally
thank you for the questions and let me try to answer all the questions :)
what I have in mind is to give after each move (die throw) the new odds should show next to the checker. the reason is that in general there will be many users watching and they will be glad to have a chance to jump into the game whenever they like. this would be very similar to a real horse racing with live in-play bets.
and to be frank I want to offer this game for a house edge with real money. and at this point I still need to figure out the house edge I should have. I mean not to much so people will love to play but enough to make some money.
and what is the chance that until the end of the game the winner ended in finish panel and one or more of the other 5 checkers didn't move at all and is still sitting on the starting panel? that means that the number of the die was not thrown even once during the game.
thanks
edit:
the idea for this question is to give out something like a bad beat price in case one player didn't move at all during a game
Quote: sevenit looks that no one paid attention to my last sentence (question) in my first posting. or if yes maybe you guys thought that the answer is obvious. here is my question again
and what is the chance that until the end of the game the winner ended in finish panel and one or more of the other 5 checkers didn't move at all and is still sitting on the starting panel? that means that the number of the die was not thrown even once during the game.
thanks
edit:
the idea for this question is to give out something like a bad beat price in case one player didn't move at all during a game
Take my expression�but start each summation at 1 (instead of 0). Also, minus one from the exponent on the 1/6. Then subtract this new expression from 1. So this�

The answer: 0.252636
The Explanation: You minus one from the exponent because now you don�t care who wins (so the last roll no longer has a 1/6 chance of happening). Also, starting each summation at 1 means each checker moved. But we want at least one checker doesn�t moved�which is simply the complement, therefore we subtract from 1.
ok. i took itQuote: PeeMcGeeTake my expression
it took me some time
but i got
(like catching a fish bare-handed like)
nothing like computing with a computer
an interesting distribution
(i have no other words that i can use)
thank you
Sally
there could be at least 1 player (checker) not moving one space by the time 1 is a winner.Quote: seventhe idea for this question is to give out something like a bad beat price in case one player didn't move at all during a game
a simple simulation shows that 1 to 5 players (checkers) could move not one space during the race
wow
1,1,1,1,1,1 WINNER! (it happened in my sim)
"RIGGED RACE!"
and agree with 25.3% as that answer
feels about right too
(abouts 20.1% of races will have just 1 checker not moving at least 1 space
and 4.2% there were 2 checkers watching each other AND the others race)
Sally
Quote: mustangsallythere could be at least 1 player (checker) not moving one space by the time 1 is a winner.
a simple simulation shows that 1 to 5 players (checkers) could move not one space during the race
wow
1,1,1,1,1,1 WINNER! (it happened in my sim)
"RIGGED RACE!"
and agree with 25.3% as that answer
feels about right too
(abouts 20.1% of races will have just 1 checker not moving at least 1 space
and 4.2% there were 2 checkers watching each other AND the others race)
Sally
@ PeeMcGee thanks again
lets see if I understood it. taking the 25.3% would mean that every 4th game at least 1 checker
will not move from the start field? or am I wrong?
Quote: seven@ PeeMcGee thanks again
lets see if I understood it. taking the 25.3% would mean that every 4th game at least 1 checker
will not move from the start field? or am I wrong?
You would expect it to happen about 1 in 4 games. Correct.
i agree tooQuote: PeeMcGeeYou would expect it to happen about 1 in 4 games. Correct.
on average that is
abouts 1 in 4 games
not every 4th game - that would be a game design if needed
but a possibility that in the next 4 games (even 8 games)
there would be not 1 game (race) where at least 1 checker did not move
averages are 1 in 4
25% is the event success probability
so they are related
but are not the same thing
Quote: mustangsallyi agree too
on average that is
abouts 1 in 4 games
not every 4th game - that would be a game design if needed
but a possibility that in the next 4 games (even 8 games)
there would be not 1 game (race) where at least 1 checker did not move
averages are 1 in 4
25% is the event success probability
so they are related
but are not the same thing
with 1 in 4 the only thing that comes to my mind is an insurance side bet that it won't happen.
as I am looking for a jackpot idea I have to ask what are chances that 111111 will happen? 6 times one of the 6 numbers in a row?
yes Sally your simulation gave me this idea :)
Quote: sevenwith 1 in 4 the only thing that comes to my mind is an insurance side bet that it won't happen.
as I am looking for a jackpot idea I have to ask what are chances that 111111 will happen? 6 times one of the 6 numbers in a row?
yes Sally your simulation gave me this idea :)
The probability that a specific number occurs six times in a row is simply (1/6)6.
The probability that any one of the numbers occurs six times in a row is (1/6)5.
Which...it should be pointed out that the 1 in 4 probability was for any one of the numbers to not move.
yes, and at least 1Quote: PeeMcGeeWhich...it should be pointed out that the 1 in 4 probability was for any one of the numbers to not move.
that seems too easy of an answer to meQuote: PeeMcGeeFor a specific number to not move�well, it would be one sixth of that or about 1 in 24.
so i looked at me sims
and they all showed between 1 in 19 to 1 in 19.4 for a specific checker not to move (i used #1 both times)
i could be wrong here too
that seems too easy too
but I have played this 6hit game many times in Excel
and it is still fun
(MAY not be fun when I be in Las Vegas next week starting tomorrow)
wow
look at this race
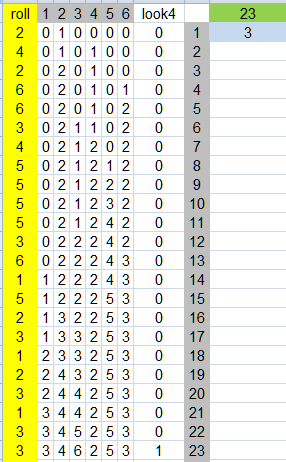
after roll 11
who bet on #3 to win?
not i
all liked #5 (me too) and one can see why
what a finish!!
and who came in second?
i did not take a photo of that
Sally
i be finished, won my Angel over, until after next week
have a fun weekend
WSOP Event #3
Quote: PeeMcGeeThe probability that a specific number occurs six times in a row is simply (1/6)6.
The probability that any one of the numbers occurs six times in a row is (1/6)5.
Which...it should be pointed out that the 1 in 4 probability was for any one of the numbers to not move. For a specific number to not move�well, it would be one sixth of that or about 1 in 24.
as it looks now it doesn't make sense to take the option - that any of the numbers will not move from start to end-. for a kind of jackpot offer.
but The probability that any one of the numbers occurs six times in a row is (1/6)5 looks not bad if I got the
number right 1/46656 (please correct me if I am wrong) and I would offer it that any number needs to show 6 times from start (= first throw) to end (=6th throw) any 6 times in a row during the game doesn't count. does it actually matter if it is from start only or at any time during the game?
so my offer for a jackpot would be that if any number is showing 6 times in a row from 1st throw all who have a bet on this
number/checker will get the jackpot and if there are more than one players on this number the jackpot must be
paid in fair parts taking each ones bet in account.
thanks
Quote: mustangsallyyes, and at least 1
that seems too easy of an answer to me
so i looked at me sims
and they all showed between 1 in 19 to 1 in 19.4 for a specific checker not to move (i used #1 both times)
i could be wrong here too
that seems too easy too
but I have played this 6hit game many times in Excel
and it is still fun
(MAY not be fun when I be in Las Vegas next week starting tomorrow)
wow
look at this race
after roll 11
who bet on #3 to win?
not i
all liked #5 (me too) and one can see why
what a finish!!
and who came in second?
i did not take a photo of that
Sally
i be finished, won my Angel over, until after next week
have a fun weekend
WSOP Event #3
now I am a bit confused. the math is telling us 1 in 24 for a specific number not to move and you are saying it is about 1 in 19.
thank you for the race sample. very interesting one for the house because it would attract many side bets.
@PeeMcGee could you please check your program and tell us what would have been the odds for the player
after the the 5th #5 showed up? after roll 15.
@Sally thanks and good luck in Vegas
Quote:now I am a bit confused. the math is telling us 1 in 24 for a specific number not to move and you are saying it is about 1 in 19.
Opps, I forgot that you can have games with multiple non-movers. Ignore my 1 in 24. I don't have time right now to do the math, but 1 in 19 sounds about right.
Quote: sevenHi all
please remember that I am no a math or formula expert and therfore I am back with a question. thanks
please look here Example
this game is played with one die and after each throw the checker with the thrown number is moved one panel ahead. here the first throw was the number 1 and the checker was moved one panel ahead. the winner is the first who will end in the finish panel.
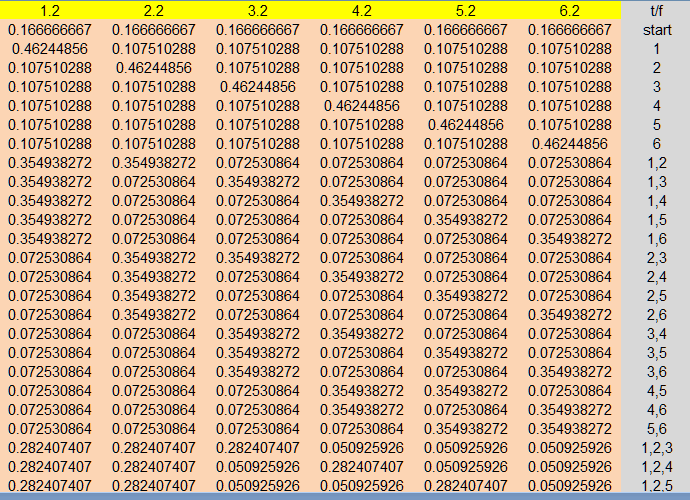
at start the chances to win is 5:1 and winner will end with 6
if you see this starting pic. what are now the chances for 1 or the others to cross the finish line first? actually chances will change after every move. what formula do I need to use to get always the right odds after each move till finish?
There is a remarkable way to solve this problem which is almost like magic. Perfect for the Wizard. The trick is to imagine that the die is rolled at points in time which are determined by a continuous Poisson points process. Clearly it makes no difference to the final answer when in time the die is rolled. We are free to imagine that these moments in time are chosen any way we want. So we choose to imagine them occurring at random points in time determined by the Poisson points process with rate 1. This means that the number of rolls that occur within any time interval depends only on the length of the time interval, independent of the number in any other interval, and it is distributed as a Poisson distribution with rate 1 so there is on average 1 roll per unit time.
Here's where the magic occurs. The rolls of the 6 numbers form 6 independent Poisson points processes each with rate 1/6. This is a basic property of Poisson points. Before we introduced the Poisson points, the players were not independent. If player 1 beat player 2, that would affect the probability that he beat the other players, so we could not simply raise the probability that he beats player 2 to the 5th power to get the probability that he beats all 5 opponents. But when we introduce the element of time in this manner with Poisson points, the probability that all of the opponents have moved 5 squares or less at a given time becomes simply the product of the probabilities for each opponent because the Poisson points for different numbers form independent Poisson points processes. Before we introduced time, if our player had moved say 4 squares in only 6 rolls, then no other player could have moved more than 2 squares. But now a player having moved 4 squares in some amount of time does not constrain in any way the number of squares the other opponents could have moved in that same amount of time because the waiting times between Poisson points are distributed as an exponential distribution which is memoryless. This allows us to compute the exact probability that player1 with the head starts wins like this:
= 223480979813228411 / 789730223053602816
≈ 0.282983952354144
In agreement with earlier calculations and a simulation.
We are integrating the probability of winning over all times since the player can win at any time. The sum inside the integral gives the probability that an opponent has rolled his number anywhere from 0 to 5 times from the Poisson distribution. We can raise this to the 5th power for the 5 opponents which are now independent. Now we want player 1 to roll his number 4 times during this time period, plus 1 more time for the win which occurs between time t and t + dt. The final one has Poisson probability (1/6)dt, and the other 4 have probability (t/6)^4/4! * e^-(t/6). The integral can be evaluated analytically by parts, and this can be facilitated by something like mathematica or the free online tool SymPy. It can also be evaluated numerically which requires nothing more than summing a sufficient number of values of the function which are spaced sufficiently closely, and then multiplying by the spacing.
The series inside the integral can be identified as the upper tail of a cumulative gamma distribution. That is, the upper incomplete gamma function normalized by Gamma(6). So we can rewrite the integral as
We can write this for general values of the the number of squares N, the number of players P, and the head start H as
In a more general game where different players have different starting points, we could replace the term raised to the P-1 power with a product of separate terms where N is replaced by the number of squares each player needs to win.
I understand that this general method is described in a book by Sheldon Ross. I first encountered it in connection with the coupon collector problem where we can use it to compute, for example, the probability distribution for the number of times the most frequently collected coupon appears by the time we have collected all of the coupons.
Here's a session where I evaluate that integral at live.SymPy.org for the original problem.

Here's a simple R program for evaluating the integral numerically just by summing.
You can do this easily in any language. R is free and can be installed in minutes. It also has a numerical integration function, but I didn't use that here. I'm summing up to t=360 in increments of 0.0036, and you can see this gives 14 decimal digits of precision by comparing to the exact answer above.
P = 6 # Players
N = 6 # Race to N
H = 1 # Head start for player 1
dt = N*P/10000
k = 0:(N-1)
prob = 0
for (t in seq(0,10*N*P,dt)) {
prob = prob + sum((t/P)^k/factorial(k)*exp(-t/P))^(P-1)*(t/P)^(N-H-1)/factorial(N-H-1)*exp(-t/P)*1/P
}
prob = prob*dt
prob
output:
[1] 0.282983952354139
Quote: sevenand what is the chance that until the end of the game the winner ended in finish and one of the other 5 checkers didn't move at all and is still sitting on the starting panel? that means that the number of the die was not thrown even once during the game.
I'll assume as others did that any player can win, not just the head start player. Here we would break this into 2 integrals with the first being for when the player with the head start wins, and the second being for one of the other 5 players wins. Then inside the integral we need to subtract the cases where all the players advance at least to the first square.
= 230919202750819 / 914039610015744
≈ 0.252635881662548
Again in agreement with earlier calculations and simulation.
I really appreciate all your guys input and views with all your formulas. and to be frank I take my hat off. but I need it ELI5 :)
what do you mean with Head start? what or who is head start? the roll of the die will decide who starts first just in case just in case you mean the head start is the one
who moves first.
thanks
you are welcome and yes it couldQuote: seventhank you for the race sample. very interesting one for the house because it would attract many side bets.Quote: mustangsallywow
look at this race
you do know this game is popular all over the world
it is a horse race game with dice
i have never seen anyone trying out math to solve for winning probs
so this IS fun
i checked it after a small sim (100,000 - should be 10M or 100x that for closer results)Quote: seven@PeeMcGee could you please check your program and tell us what would have been the odds for the player
after the the 5th #5 showed up? after roll 15.
my sim in Excel (no vba just a little add-in used)
Player probs to win the race after the 15th roll
current positions
1,2,2,2,5,3
1: 1100 >> 0.011
2: 3264 >> 0.03264
3: 3248 >> 0.03248
4: 3221 >> 0.03221
5: 79699 >> 0.79699
6: 9468 >> 0.09468
calculated with the python code
(have not yet converted this to R code
and it now will be a 2 player race!)
1: 0.010940937
2: 0.032622172
3: 0.032622172
4: 0.032622172
5: 0.796962623
6: 0.094229924
you can take the probability distribution and create a payout table
that looks like fun too!
WSOP Event #3 coming on the 28th!
Sally
like magically delicious (think lucky charms)Quote: BruceZThere is a remarkable way to solve this problem which is almost like magic.
Hi Bruce!Quote: BruceZPerfect for the Wizard.
in what way exactly?
(I ask that question a lot)
where have you been hiding?Quote: BruceZ<snip>
you do not have to answer (love you!)
OK
the solution you showed
looks nice
but it took me almost forever to get PeeMcGee's method down
(i got it and was still going to work with R using the python code)
not many chances to use the negative multinomial distribution these days with power singers like Katy Perry and Lady Gaga
around
welcome BruceZ to WoV
you going to be at WSOP Event #3
see you there (come out west and visit)
Sally
Quote: seven
what do you mean with Head start? what or who is head start?
I just mean player 1 has a head start of 1 square since he starts already 1 square ahead of the others before the first roll.
Quote: mustangsallyHi Bruce!
in what way exactly?
(I ask that question a lot)
Hi Sally! I think in all my years doing probability, that had to be about the weirdest calculation method I've run across. I think you can appreciate the subtlety. A naive person might simply try to use the fact that in a heads up match between 2 players where 1 player has a 1 square head start and we ignore all other numbers, that player wins about 62.3% of the time (since he just has to win at least 5 out of 10 times that one of their numbers come up). Then they might try to just raise 0.623 to the 5th power to get the probability that he beats all 5 opponents. Of course that doesn't work (you get only about 9.4%) since if he beats player 2, he is more likely to beat the others. That is, they are not independent. But then we pull this continuous time Poisson process idea out of thin air, and POOF, suddenly they are independent. It can take some time to get your head around what just happened. It's a powerful technique. It allows you to answer all kinds of tough looking questions.
Quote: mustangsallywhere have you been hiding?
you do not have to answer (love you!)
Lurking in the shadows. I missed you too.
Quote: mustangsallyOK
the solution you showed
looks nice
but it took me almost forever to get PeeMcGee's method down
(i got it and was still going to work with R using the python code)
You can answer the OPs first question with 2 lines in R:
> t = seq(0,5000,.01)
> sum((1-pgamma(t/6,6))^5*(t/6)^4/factorial(4)*exp(-t/6)*1/6)*.01
[1] 0.282983952354144
We could have 100 players with a 100-sided die, and you wouldn't need 99 nested sums. You would only need the one integral which is like 1 sum. Then we can easily modify this to do the more general problem where different players start on different squares. Also where the die is loaded.
Quote: mustangsally
you do know this game is popular all over the world
it is a horse race game with dice
i have never seen anyone trying out math to solve for winning probs
so this IS fun
i checked it after a small sim (100,000 - should be 10M or 100x that for closer results)
my sim in Excel (no vba just a little add-in used)
Player probs to win the race after the 15th roll
current positions
1,2,2,2,5,3
1: 1100 >> 0.011
2: 3264 >> 0.03264
3: 3248 >> 0.03248
4: 3221 >> 0.03221
5: 79699 >> 0.79699
6: 9468 >> 0.09468
calculated with the python code
(have not yet converted this to R code
and it now will be a 2 player race!)
1: 0.010940937
2: 0.032622172
3: 0.032622172
4: 0.032622172
5: 0.796962623
6: 0.094229924
you can take the probability distribution and create a payout table
that looks like fun too!
WSOP Event #3 coming on the 28th!
Sally
thanks for pointing me to google for horse racing with dice :) stupid me that I didn't do it before. but what I found is that all games are played with 2 dice and cards or 3-5 dice. I didn't find one that was played with 1 die. and as you mentioned I didn't find one that gives odds. so I will stick to the idea :)
thanks again for the probs of the specific race situation. need yet to figure out what odds the bookmaker is giving (odds less his %). need to see what a healthy % would be.
yes of courseQuote: sevenneed yet to figure out what odds the bookmaker is giving (odds less his %).
need to see what a healthy % would be.
for the race i showed after the 15th roll
it could be something like this
player5 is such an odds on favorite to win at abouts 80%, the odds offered in this example are 1:5 (bet 5 to win 1)
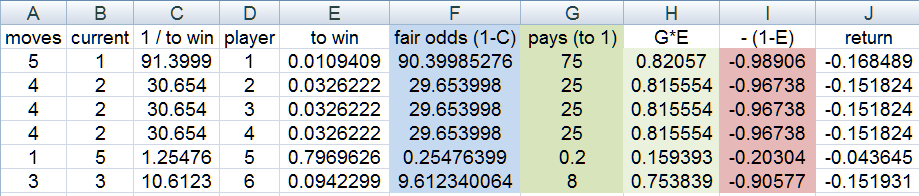
of course the odds to start the race will be the same and the choices are small
after 1 roll you could have this
the one that moves first on the 1st roll could be now at 12:5 odds

after 2 roll you could have this
with two players at square 1 being the most common position for the race
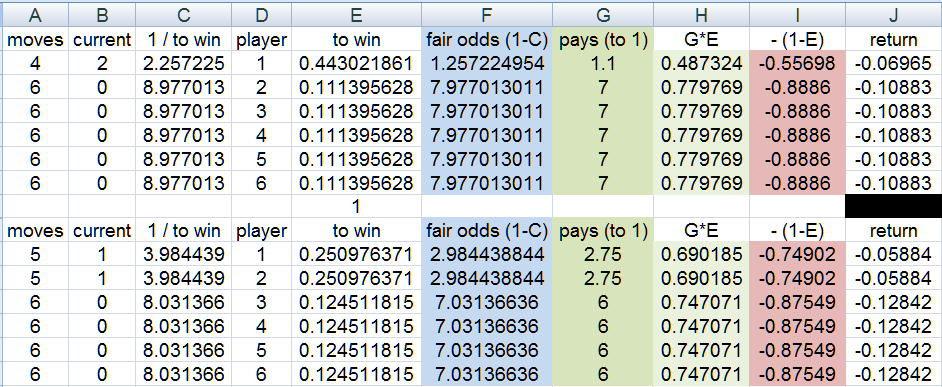
after 3 roll you could have this
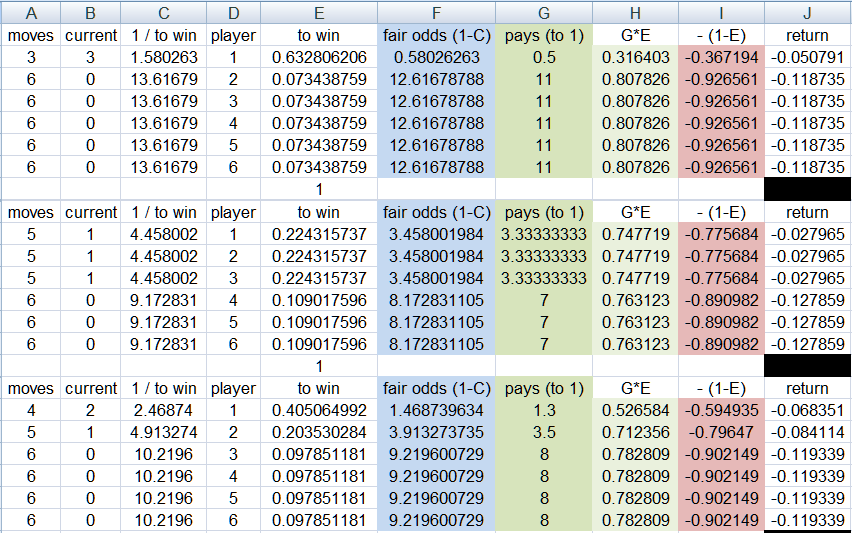
and so on
after 15 rolls (the race is still on)
there could be lots and lots of race positions (33 i count)
likes (player order does not matter)
5,5,5,0,0,0
5,5,4,1,0,0
5,5,3,1,1,0
5,5,2,2,1,0
...
3,3,3,2,2,2 <<<the race is very close here
(these could be states in a Markov chain i thinks)
and each race position (state) needs to have the correct probability for winning and odds to offer
fun
Sally
interesting seq()Quote: BruceZYou can answer the OPs first question with 2 lines in R:
> t = seq(0,5000,.01)
> sum((1-pgamma(t/6,6))^5*(t/6)^4/factorial(4)*exp(-t/6)*1/6)*.01
[1] 0.282983952354144
i see that values down to (0,100,,01) works well too
see, more to learn
yes we couldQuote: BruceZWe could have 100 players with a 100-sided die,
and the length of that game would be way longer on average than a 6 player race
unless more dice are rolled each time
more to my liking, yesQuote: BruceZand you wouldn't need 99 nested sums. You would only need the one integral which is like 1 sum.
weQuote: BruceZThen we can easily modify this to do the more general problem where different players start on different squares.
oh yes
you and PeeMcGee (and MAY be just a few others)
i would test that code after "we" does the easy modification
of courseQuote: BruceZAlso where the die is loaded.
a nice way to complete the picture
thank you Bruce
Sally
What a great first post. That solution is indeed magical. That connection to the coupon problem is great�I actually had that come up recently. Thanks for sharing it.
Quote: mustangsallyyes of course
for the race i showed after the 15th roll
it could be something like this
player5 is such an odds on favorite to win at abouts 80%, the odds offered in this example are 1:5 (bet 5 to win 1)
fun
Sally
thanks for the posting. did you use any code key to come up with the >pays (to 1)< compared to the fair odds?



