questions and answers for Wizard: Blackjack win/stop question

Hi ,I read your great website regularly from my country Iran, and since there is no such thing as blackjack (only underground poker homegames) I can only read the theory ,I have studied mathematics as my Bachelor and it never ceases to amaze me how you break down these bj-related questions, thank you anyhow for the great job.

on my eurotrip this week, I met another proplayer, who had a very weird system ,we talked a bit about the mathematics aspect of what he does ,yet I was not actually convinced .
He told me 5 nights per week(which is irrelevant), he comes with 150€ and bets on two boxes,each of them 2€ in total 4€ per hand , and the moment he is up 28€ he leaves the casino,as I monitored his way of play, he was using the optimal blackjack system exactly according to the charts on wizardofodds or other websites. the deck is shuffled continuously here,6 decks, the dealer stands on s17. I asked him and he specified .he keeps betting as long as he has 178€ (28€up) or 50€(100€ down), both ways he stops betting. according to his own notes ,the last time he had lost was on 18th of July 2013.so basically he makes around 1k€ per month.
but I am not convinced why he'd choose 28€ (around 18%) up as the leaving point? do you think thats different than setting a time-limit or hands-limit? lets say I will play 150 hands and will leave no matter up or down. he insisted on having a better chance on 18% win , the problem was I was not able to communicate in German to understand the logic behind this. and also I do not understand whats the difference between leaving the table and playing tomorrow or staying and playing another session right after the first session, since the deck is being shuffled constantly.
would be great to know if you find his logic bs or not.
cheers

Quote: alexBerlin

Hi ,I read your great website regularly from my country Iran, and since there is no such thing as blackjack (only underground poker homegames) I can only read the theory ,I have studied mathematics as my Bachelor and it never ceases to amaze me how you break down these bj-related questions, thank you anyhow for the great job.

on my eurotrip this week, I met another proplayer, who had a very weird system ,we talked a bit about the mathematics aspect of what he does ,yet I was not actually convinced .
He told me 5 nights per week(which is irrelevant), he comes with 150€ and bets on two boxes,each of them 2€ in total 4€ per hand , and the moment he is up 28€ he leaves the casino,as I monitored his way of play, he was using the optimal blackjack system exactly according to the charts on wizardofodds or other websites. the deck is shuffled continuously here,6 decks, the dealer stands on s17. I asked him and he specified .he keeps betting as long as he has 178€ (28€up) or 50€(100€ down), both ways he stops betting. according to his own notes ,the last time he had lost was on 18th of July 2013.so basically he makes around 1k€ per month.
but I am not convinced why he'd choose 28€ (around 18%) up as the leaving point? do you think thats different than setting a time-limit or hands-limit? lets say I will play 150 hands and will leave no matter up or down. he insisted on having a better chance on 18% win , the problem was I was not able to communicate in German to understand the logic behind this. and also I do not understand whats the difference between leaving the table and playing tomorrow or staying and playing another session right after the first session, since the deck is being shuffled constantly.
would be great to know if you find his logic bs or not.
cheers

alexBerlin,

Welcome to the forum! Very cool to have a player from Iran.

I hope the Wizard answers you directly. Some other folks may as well. I don't have the math skills to give you the type of answer you're requesting.

You already answered your own question. Whether you bet today or tomorrow, the house edge remains the same, especially for csms. This guy is not a pro, just a gambler

Welcome to the forum. As far as I know, you are our first Iranian member.

This answer may come off as rude, but I tell it like it is. As I have said hundreds of times, all betting systems are equally worthless. There are no magic markers to get up and quit playing, either up or down. Many gamblers fool themselves with systems that either win a little or lose a lot. For most sittings, such systems do win, but in the long run, you'll lose as much with that as any other system.

Quote: alexBerlin

Hi ,I read your great website regularly from my country Iran, and since there is no such thing as blackjack (only underground poker homegames) I can only read the theory ,I have studied mathematics as my Bachelor and it never ceases to amaze me how you break down these bj-related questions, thank you anyhow for the great job.

on my eurotrip this week, I met another proplayer, who had a very weird system ,we talked a bit about the mathematics aspect of what he does ,yet I was not actually convinced .
He told me 5 nights per week(which is irrelevant), he comes with 150€ and bets on two boxes,each of them 2€ in total 4€ per hand , and the moment he is up 28€ he leaves the casino,as I monitored his way of play, he was using the optimal blackjack system exactly according to the charts on wizardofodds or other websites. the deck is shuffled continuously here,6 decks, the dealer stands on s17. I asked him and he specified .he keeps betting as long as he has 178€ (28€up) or 50€(100€ down), both ways he stops betting. according to his own notes ,the last time he had lost was on 18th of July 2013.so basically he makes around 1k€ per month.
but I am not convinced why he'd choose 28€ (around 18%) up as the leaving point? do you think thats different than setting a time-limit or hands-limit? lets say I will play 150 hands and will leave no matter up or down. he insisted on having a better chance on 18% win , the problem was I was not able to communicate in German to understand the logic behind this. and also I do not understand whats the difference between leaving the table and playing tomorrow or staying and playing another session right after the first session, since the deck is being shuffled constantly.
would be great to know if you find his logic bs or not.
cheers

Basically his system is to risk €100 to win €28. That's going to work most of the time, but when it doesn't, he loses the full €100.

He prefers to risk a lot to win a little. Some prefer to risk a little to win a lot. In the end it doesn't matter at all. In the long run he will lose an amount equal to the house edge multiplied by his total action.

By "stopping" when up €28, he is putting an arbitrary "session" label when in reality there are no "sessions." It's just one long game and your friend is just another losing gambler.

A family member has been using the method for some time now and stands by his claim of an 80% success rate. He brings a bankroll of 20X, bets X always, and his target is 5X. How would I setup the formula to calculate the probability of achieving 5X or losing 20X?

P.S., Thank you for creating the informative websites/forums!

Quote: elee1978

A family member has been using the method for some time now and stands by his claim of an 80% success rate. He brings a bankroll of 20X, bets X always, and his target is 5X. How would I setup the formula to calculate the probability of achieving 5X or losing 20X?

You would expect to win a particular amount four times as often as lose four times that amount. The claim is hardly surprising.

Looks like a straightforward Gambler's Ruin problem. However, you need to know what the probability of winning is.

If it's a straight 50/50 game, the the probability of getting to 5X before -20X is 20 / (20 + 5) = 80%.

OOPS - earlier answer has been corrected
If it is something else, then the probability is (1 - X²⁰) / (1 - X²⁰⁺⁵),
where X = (probability of losing) / (probability of winning)
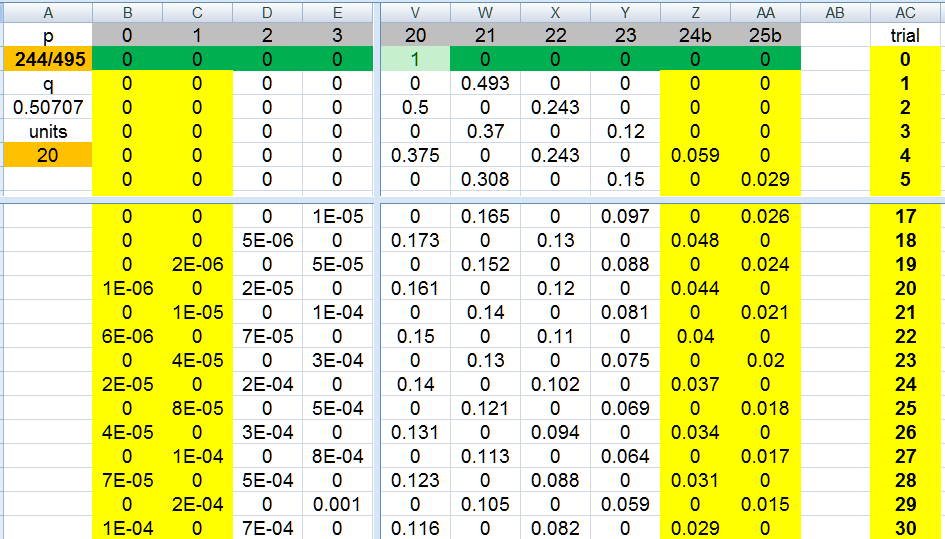
For the pass line in craps, X = (251/495) / (244/495) = 251/244, and the probability is 73.98522%.

Quote: ThatDonGuy

You would expect to win a particular amount four times as often as lose four times that amount. The claim is hardly surprising.

Looks like a straightforward Gambler's Ruin problem. However, you need to know what the probability of winning is.

If it's a straight 50/50 game, the the probability of getting to 5X before -20X is 20 / (20 + 5) = 80%.

of course this does not consider a time factor that could be important
for this example of 20 to 25 at 50% = 100 games on average
of that either ruin or success

for just success i get simulated = 75 games
and one could still be playing after 254 games played with a calculated prob of abouts 10%
see (C)

Quote: ThatDonGuy

If it is something else, then the probability is (1 - X)²⁰ / (1 - X)²⁰⁺⁵, or (1 - X)⁴ / (1 - X)⁵,
where X = (probability of losing) / (probability of winning)
For the pass line in craps, X = (251/495) / (244/495) = 251/244, and the probability is 78.853%.

Oh, check your math
me thinks the pass line success prob is too high

now,
I use Excel for a simple recursion table when i wants to see the time distribution
just add and multiply (well, Excel does it after filling in one row with simple formulas)
there are a few other methods one could also use, Feller showed one too, but i like this for now

here is for the pass line
again, time could be a factor, waiting for ruin or success


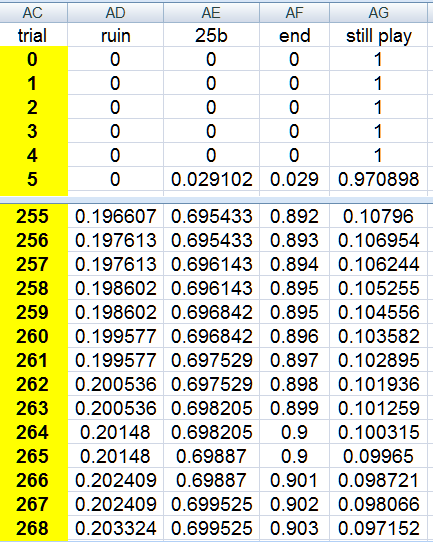
here is a small view of me spreadsheet


Sally

Quote: elee1978

A family member has been using the method for some time now and stands by his claim of an 80% success rate.
He brings a bankroll of 20X, bets X always, and his target is 5X.

How would I setup the formula to calculate the probability of achieving 5X or losing 20X?

Ahhh, very nice question i say

i gather you are talking about playing blackjack

if not
this will work also for other games too
(it is one method to use and is not perfectly exact but gets very good results most times)

but more info is needed
like the rules of the game
playing basic strategy or ?

Don Schlesinger and Alan Krigman come to mind for formulas to work with

you need to know
the edge, variance or standard deviation for one bet
and the other values can be used as bankroll units from the bet unit

i get abouts 78.1% chance of success for one attempt
about same as calculating with a Markov chain but i used a 6 deck prob distribution for that

here is a pic from me Excel
I could add this spreadsheet to my online folder (i have to get back to my computer first)
Alan Krigman made it but he passed away last year (i added lots of color too)



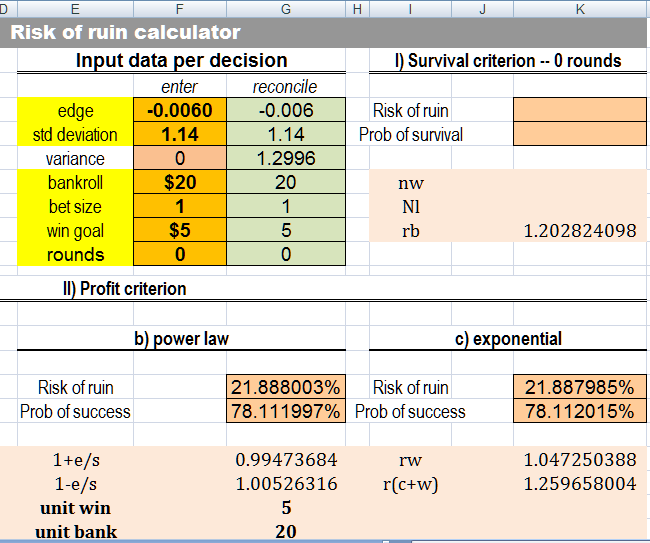
the formula for c) exponential
in Excel
risk of ruin =((1/K19)-1) / ((1/K20)-1)
K19 =EXP((-2*edge*unitwin)/var)
K20 =EXP((-2*edge*(unitwin+unitbank))/var)
unitwin = 5
unitbank = 20

not just your average 2 + 3 = X type formula
computers are what they are

Sally

Quote: mustangsally

Quote: ThatDonGuy

If it is something else, then the probability is (1 - X)²⁰ / (1 - X)²⁰⁺⁵, or (1 - X)⁴ / (1 - X)⁵,
where X = (probability of losing) / (probability of winning)
For the pass line in craps, X = (251/495) / (244/495) = 251/244, and the probability is 78.853%.

Oh, check your math

It's not the math I need to check - it's the formula.

It's not (1 - X)²⁰ / (1 - X)²⁰⁺⁵; it's (1 - X²⁰) / (1 - X²⁰⁺⁵), which is 73.98522%.
This is in line with the simulation I ran.

Quote: ThatDonGuy

It's not the math I need to check - it's the formula.

It's not (1 - X)²⁰ / (1 - X)²⁰⁺⁵; it's (1 - X²⁰) / (1 - X²⁰⁺⁵), which is 73.98522%.
This is in line with the simulation I ran.

i sometimes use that formula in Excel but could not write it out from memory correctly 100% of the time

I have bunches of Markov chains (transition matrices) in Excel and i like to see lots more data
as Excel certainty loves to do these too

yes, i see the value starting with 20 units

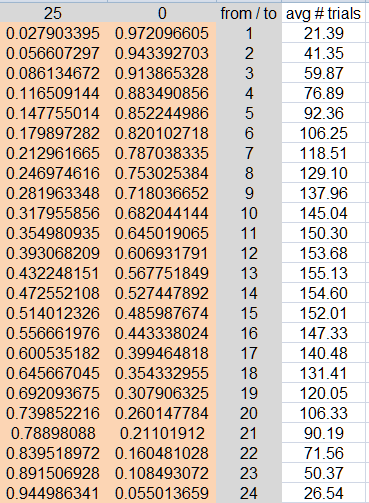
btw, the avg # trials (in me photo) is for either ruin or win goal
it takes a different matrix for just ruin or just success
maybe i add those to my online folder later too

the from / to column is the starting bankroll



Sally says "time matters when having fun!"

in other words...
"more time, more fun!"

Quote: mustangsally

I have bunches of Markov chains (transition matrices) in Excel and i like to see lots more data
as Excel certainty loves to do these too

btw, the avg # trials (in me photo) is for either ruin or win goal
it takes a different matrix for just ruin or just success
maybe i add those to my online folder later too

I know the general formula for the expected number of trials overall, but are there formulas for the expected number of trials in a success, or in a failure? Or do those have to be estimated?

Quote: ThatDonGuy

I know the general formula for the expected number of trials overall,

yes, i remember

Quote: ThatDonGuy

but are there formulas for the expected number of trials in a success, or in a failure?

i have looked b4
more than 1 time
and found none

one day when BruceZ, over at 2+2 forum, was helping Steen, with WinCraps,
Bruce posted a formula for it, I think Steen asked, and mentioned
he never did think anybody had ever asked about it before

I do remember not agreeing with his answer but was doing something else at the time

as they can easily be arrived at using a Markov chain or a simple recursive table, in my opinion
both, I use with a backup sim

i think i will look into that again
i went to the store and do have lots of skittles and chicken noodle soup

1st i must find that info i have, i bought and use a different laptop now
so the info i would want may have a new resting location
Sally

added: for this pass line example 20 into 25
I get given a win
73.99493948 average games played (using Excel)

that sure looks like the success prob at 0.739852216

interesting

given a loss
have not calculated that one yet

Quote: ThatDonGuy

I know the general formula for the expected number of trials overall, but are there formulas for the expected number of trials in a success, or in a failure?

I found them.
I thought Feller had them but that was not true

should have known it was SN Ethier in his Doctrine of Chances book
there is so much in that book (over 800 pages of fun)

here are the photos
they are very nice

when p<>q

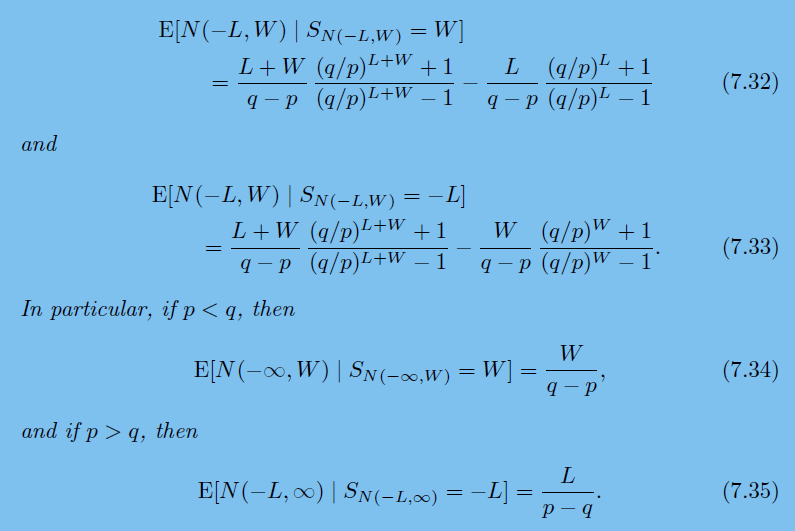
when p=q


works sweet
see (C)
for turning 20 into 25 and p=0.50


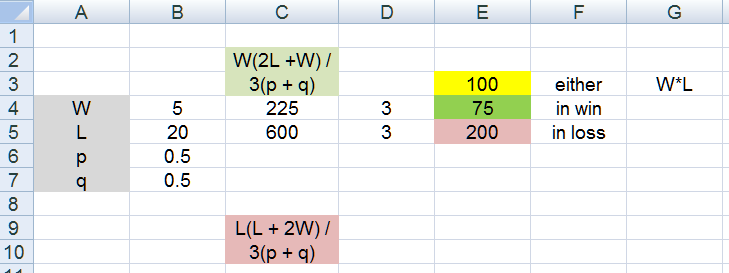
for turning 20 into 25 and p=244/495


example when W=L or trying to double the starting bankroll
note the mean times are all equal


Prof Ethier added this
"Proof. This is a tedious but straightforward calculus problem."

of course averages can still be skewed
we can always look at the actual distribution for a warm feeling inside too

Thank you!
love learning something new
Sally

Thank you so much to you and ThatDonGuy for the information and Excel examples (I'd be lost w/out these!!); and especially for teaching me something new!! This is a bit worse than my family member's approximation of an ~80% success rate. He'll be (un)happy to know that it's worse than 1 in 4 as opposed to 1 in 5.

Quote: elee1978

Thank you so much to you and ThatDonGuy for the information and Excel examples (I'd be lost w/out these!!); and especially for teaching me something new!!

yes sure was fun!

this file
RoR-AlanK.xls

can be found in my Microsoft online folder
the link is in my blog
https://wizardofvegas.com/member/mustangsally/blog/#post1094

more advanced math is required when more advanced betting is used
in the game of blackjack
of course that has also been done too
Don Schlesinger sure was a busy guy

I wonder if he may also be a good singer
lucky man
Sally