Recommended online casinos

Wizard
Administrator
Wizard
Wizard
  • Threads: 1518
  • Posts: 27036
Joined: Oct 14, 2009
May 12th, 2014 at 4:51:28 PM permalink
What is the probability of achieving a Yahtzee after ten rolls?

For those who don't understand the question, here are the rules:

1. Five six-sided dice are rolled.
2. The object is to have all of them on the same face, for example all twos.
3. After any roll you may hold any dice you wish and re-roll the others.
4. Switching to a different number is allowed. For example if you roll 1-1-2-3-4 on the first roll, then hold the ones, and then roll a 2-2-2 with the other three, having 1-1-2-2-2, then you can switch to holding the twos and re-roll the ones.

Normally in the game of Yahtzee you get only three rolls, but I'm allowing ten (to make it harder).

For extra credit, what is the probability after 1 to 9 rolls?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
beachbumbabs
beachbumbabs
beachbumbabs
  • Threads: 101
  • Posts: 14268
Joined: May 21, 2013
May 12th, 2014 at 4:55:21 PM permalink
Quote: Wizard

What is the probability of achieving a Yahtzee after ten rolls?

For those who don't understand the question, here are the rules:

1. Five six-sided dice are rolled.
2. The object is to have all of them on the same face, for example all twos.
3. After any roll you may hold any dice you wish and re-roll the others.
4. Switching to a different number is allowed. For example if you roll 1-1-2-3-4 on the first roll, then hold the ones, and then roll a 2-2-2 with the other three, having 1-1-2-2-2, then you can switch to holding the twos and re-roll the ones.

Normally in the game of Yahtzee you get only three rolls, but I'm allowing ten (to make it harder).

For extra credit, what is the probability after 1 to 9 rolls?



So, you're allowing UP TO 10 rolls, stopping on any Yahtzee, in the original question, right? Which means the extra credit question would also be all-inclusive (additive)? Or you're looking for EXACTLY each number of rolls, not less (I don't think this is the question, but making sure).
If the House lost every hand, they wouldn't deal the game.
chrisr
chrisr
chrisr
  • Threads: 13
  • Posts: 141
Joined: Dec 9, 2013
May 12th, 2014 at 5:12:17 PM permalink
how i would solve it.

first we have to figure out how many matches we should start with before we continue toward our target of 5 matching. For example, if our first roll is 2 matches, should we throw it out and re-roll all 5 or should we keep the two and try to make it with the other 3 dice...

..after that it is pretty straightforward to calculate the probability.
kubikulann
kubikulann
kubikulann
  • Threads: 27
  • Posts: 905
Joined: Jun 28, 2011
May 12th, 2014 at 5:58:26 PM permalink
Quote: beachbumbabs

So, you're allowing UP TO 10 rolls, stopping on any Yahtzee, in the original question, right? Which means the extra credit question would also be all-inclusive (additive)? Or you're looking for EXACTLY each number of rolls, not less (I don't think this is the question, but making sure).

If you get a Yahtzee before the end, just keep all five dice. So both questions are equivalent.
Reperiet qui quaesiverit
mustangsally
mustangsally
mustangsally
  • Threads: 25
  • Posts: 2463
Joined: Mar 29, 2011
May 12th, 2014 at 5:58:35 PM permalink
Quote: Wizard

What is the probability of achieving a Yahtzee after ten rolls?

I love Yahtzee,
well used to play it a lot and changing rules to the game.

This actually in school was the first exercise in combinations and matrix algebra.
I could not do this in class. I had to have lots of help.

since then I have some of this in Excel for the 5 kinds
this is my transition matrix (I changed it to include a 0 state)
and the matrix raised to 10
so I think you want as an answer 1-[1,6]

even show the expected number of visits to each state (yellows)


I also have this just using recursion in Excel. many do not know how to raise a matrix to a power in Excel and that is OK.
a few formulas in a few cells is all that is required for the recursion method
I will link to it as soon as I finish it.
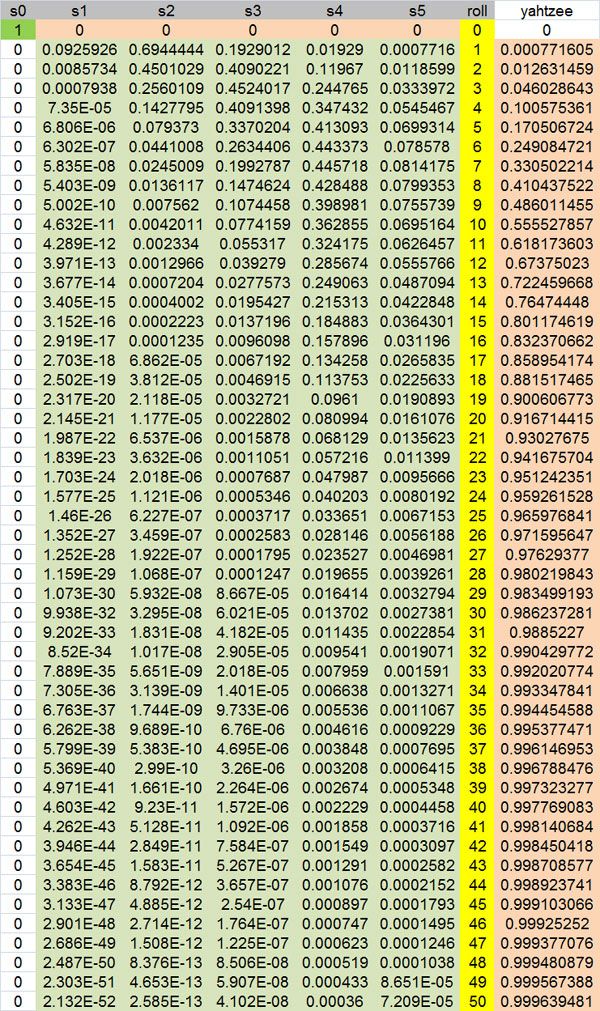
looks like this for the first 50 rolls


here is one place to start for any interested in a quick read, there really are many of them
http://www.datagenetics.com/blog/january42012/
Sally
I Heart Vi Hart
Wizard
Administrator
Wizard
Wizard
  • Threads: 1518
  • Posts: 27036
Joined: Oct 14, 2009
May 12th, 2014 at 6:09:42 PM permalink
Quote: kubikulann

If you get a Yahtzee before the end, just keep all five dice. So both questions are equivalent.



Yes, keeping all five is allowed? So asking about a Yahtzee in ten rolls could also be stated as "ten or less."
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
chrisr
chrisr
chrisr
  • Threads: 13
  • Posts: 141
Joined: Dec 9, 2013
May 12th, 2014 at 6:18:25 PM permalink
I came up with it being slightly more advantageous to re-roll all 5 dice if you don't have at least a pair.. The numbers i came up with for Yahtzee in 10 or less rolls were 0.545 and 0.550 depending on if you keep an arbitrary single die when you have less than a pair.
Tomspur
Tomspur
Tomspur
  • Threads: 28
  • Posts: 2019
Joined: Jul 12, 2013
May 12th, 2014 at 6:20:19 PM permalink
Quote: chrisr

I came up with it being slightly more advantageous to re-roll all 5 dice if you don't have at least a pair.. The numbers i came up with for Yahtzee in 10 or less rolls were 0.545 and 0.550 depending on if you keep an arbitrary single die when you have less than a pair.



edit: That is what I get for trying to be clever and then my spoiler tags don't work either :)
“There is something about the outside of a horse that is good for the inside of a man.” - Winston Churchill
AxiomOfChoice
AxiomOfChoice
AxiomOfChoice
  • Threads: 32
  • Posts: 5761
Joined: Sep 12, 2012
May 12th, 2014 at 6:22:04 PM permalink
Quote: chrisr

I came up with it being slightly more advantageous to re-roll all 5 dice if you don't have at least a pair.. The numbers i came up with for Yahtzee in 10 or less rolls were 0.545 and 0.550 depending on if you keep an arbitrary single die when you have less than a pair.



This has to be a rounding error. Keeping all 5 and keeping 4 out of 5 are identical.

To see this, imagine that, once you decide which dice to re-roll, you roll them one at a time. If you re-roll all 5, doesn't matter how the first die comes up.
chrisr
chrisr
chrisr
  • Threads: 13
  • Posts: 141
Joined: Dec 9, 2013
May 12th, 2014 at 6:58:55 PM permalink
ok.. im over thinking things.. i thought it was a trick question and there was some non-obvious strategy
Wizard
Administrator
Wizard
Wizard
  • Threads: 1518
  • Posts: 27036
Joined: Oct 14, 2009
May 12th, 2014 at 7:32:01 PM permalink
Quote: Tomspur

edit: That is what I get for trying to be clever and then my spoiler tags don't work either :)



I fixed it, as well as in all the replies.

Here is how to make a spoiler tag correctly. Don't forget to close it off.



About your comment, I agree with Axiom. If you roll five different numbers the odds are the same whether you re-roll all five or keep one. When you re-roll all of them, the first one has to be something. May as well be whatever you held.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
AxiomOfChoice
AxiomOfChoice
AxiomOfChoice
  • Threads: 32
  • Posts: 5761
Joined: Sep 12, 2012
May 12th, 2014 at 7:48:18 PM permalink
I think that this is a state machine question. Similar to your analysis of the fire bet in craps. Unless there is some shortcut that I'm missing?
chrisr
chrisr
chrisr
  • Threads: 13
  • Posts: 141
Joined: Dec 9, 2013
May 12th, 2014 at 8:27:50 PM permalink
i agree with axiom too.. the problem was i'm dumb..

i think this is the exact answer.

719605786368173972069/1295354998363672018944=0.555528...
Wizard
Administrator
Wizard
Wizard
  • Threads: 1518
  • Posts: 27036
Joined: Oct 14, 2009
May 12th, 2014 at 8:36:56 PM permalink
Congratulations! Many of you got the right answer.

This table shows the probability of having a maximum of 1 to 5 for 1 to 20 rolls.

Roll 1 2 3 4 5
1 0.092593 0.694444 0.192901 0.019290 0.000772
2 0.008573 0.450103 0.409022 0.119670 0.012631
3 0.000794 0.256011 0.452402 0.244765 0.046029
4 0.000074 0.142780 0.409140 0.347432 0.100575
5 0.000007 0.079373 0.337020 0.413093 0.170507
6 0.000001 0.044101 0.263441 0.443373 0.249085
7 0.000000 0.024501 0.199279 0.445718 0.330502
8 0.000000 0.013612 0.147462 0.428488 0.410438
9 0.000000 0.007562 0.107446 0.398981 0.486011
10 0.000000 0.004201 0.077416 0.362855 0.555528
11 0.000000 0.002334 0.055317 0.324175 0.618174
12 0.000000 0.001297 0.039279 0.285674 0.673750
13 0.000000 0.000720 0.027757 0.249063 0.722460
14 0.000000 0.000400 0.019543 0.215313 0.764744
15 0.000000 0.000222 0.013720 0.184883 0.801175
16 0.000000 0.000124 0.009610 0.157896 0.832371
17 0.000000 0.000069 0.006719 0.134258 0.858954
18 0.000000 0.000038 0.004692 0.113753 0.881517
19 0.000000 0.000021 0.003272 0.096100 0.900607
20 0.000000 0.000012 0.002280 0.080994 0.916714


I used the same matrix algebra method as Sally.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
miplet
miplet
miplet
  • Threads: 5
  • Posts: 2142
Joined: Dec 1, 2009
May 12th, 2014 at 8:42:00 PM permalink
Quote: chrisr

i agree with axiom too.. the problem was i'm dumb..

i think this is the exact answer.

719605786368173972069/1295354998363672018944=0.555528...


I agree. Here are my results. I was too lazy to reduce each fraction.
1: 1 / 1296 = appx 0.00077160493827160493
2: 21216 / 1679616 = appx 0.01263145861911294010
3: 100194336 / 2176782336 = appx 0.04602864252569899574
4: 283734147456 / 2821109907456 = appx 0.10057536103294313636
5: 623399596862976 / 3656158440062976 = appx 0.17050672367804666817
6: 1180258395057616896 / 4738381338321616896 = appx 0.24908472129760592120
7: 2029594997084335497216 / 6140942214464815497216 = appx 0.33050221386283068293
8: 3266533144426311284391936 / 7958661109946400884391936 = appx 0.41043752200278199464
9: 5012928607539358074171949056 / 10314424798490535546171949056 = appx 0.48601145536229757477
10: 7426015595376026998398845976576 / 13367494538843734067838845976576 = appx 0.55552785705632799412
“Man Babes” #AxelFabulous
RSS Feed
  • Jump to: