Anyhow I have been doing some more reading trying to understand this issue and found that at the core of my resistance to the mainstream position is that finding a finite value for the sum of an infinite geometric series appears impossible. This assumption that it is possible, seems to be at the root of all the proofs that show .99... Equals 1.
Consider the series 0.3+ 0.03+ 0.003... Most will agree that it is an infinite series i.e. it has no last term, and continues forever. Most will also agree that there is no term n for which the sum of the series equals exactly 1/3, except for n=infinity. This is where I have the issue. I know that "when" is not a definable math term but If someone could give me a general idea of when it adds up to exactly 1/3 that would help me tremendously.
Is it before or after the terms continue on forever?
Before would be impossible as it would not then be an infinite series
After seems equally impossible as there is no last term or "after"
Some may say it is neither, it is more of while it's in an infinite state, but that seems to be the same as the before position and implies that it was not In fact infinite, or that the total could go above 1/3.
Perhaps the question cannot be answered because there is no when? If there is no when, how did it happen?
Yeah, limits are what something goes to as something else goes to infinity. In this case, .3+.03+.003+...->1/3, as the number of terms goes to infinity the sum goes to 1/3. The limit gives us that for any tiny number, no matter how small, there exists a number terms that if you add them up the difference between the limit (1/3) and the sum of those terms will be less than that tiny number. Using that definition it makes sense to say that infinite number of terms sums to the limit.Quote: 1call2manyLimits I do not know. Are they the numbers that the series heads towards? In the example above the limit is 1/3?
Wikipedia's limit article is good as of my last reading of it
Quote: 1call2manyNo I have not, from what I have read it sounds like convergence heads towards zero, 1/2 + 1/4 + .... And Divergence heads towards infinity 9 + 90 + 900...? Limits I do not know. Are they the numbers that the series heads towards? In the example above the limit is 1/3?
That actually isn't true. For a convergent series the terms have to tend to zero but that is not enough to guarantee the series converges. For instance the series 1/1+1/2+1/3+... diverges as the sum tends to infinity. If you are interested I wrote a post awhile ago about geometric series and you can check it out at http://www.bubblews.com/news/2407002-9999991 . Hopefully it is pretty straight forward but if you have any questions just ask and I'll try to answer.
Wikipedia's limit article is good as of my last reading of it
It sounds like you are saying what I thought I already knew that the further you care to travel along the series, the tinier the difference between sum and limit? Or no matter how small a number we think of we can add more terms to get a little closer and hence a smaller difference?
That says to me we will never reach the limit. ( how could you reach anything with no end to the addition). I notice the Wikipedia link kept using the term arbitrarily close, is arbitrarily close, close enough to say let's just roll with it, it makes all our calculus work, etc.etc. There must be more to it, mathematitions like to be precise, arbitrarily close and acts like it's there, does not seem like a compelling reason to believe that it can sum to the limit.
Quote: 1call2manyOn a side note how do you quote someone hear and get that nice grey box? My attempt does not look like that.
There's a quote button at the bottom right of each post. It prefills the reply box with some code and you enter your response after it.
Quote: 1call2manyIt sounds like you are saying what I thought I already knew that the further you care to travel along the series, the tinier the difference between sum and limit? Or no matter how small a number we think of we can add more terms to get a little closer and hence a smaller difference?
Both, really. No matter how small a number we can think of, once you've added enough terms, you'll not only be closer, but never be further again, no matter how many more terms you add. For that to be true, the difference has to keep getting smaller and smaller as you add more terms.
Quote: 1call2manyThat says to me we will never reach the limit. ( how could you reach anything with no end to the addition). I notice the Wikipedia link kept using the term arbitrarily close, is arbitrarily close, close enough to say let's just roll with it, it makes all our calculus work, etc.etc. There must be more to it, mathematitions like to be precise, arbitrarily close and acts like it's there, does not seem like a compelling reason to believe that it can sum to the limit.
It does so by definition. An infinite sum is a kind of limit, and a repeating decimal is a kind of infinite sum. Since that's what's meant in the first place, it's proper to talk about them being what they're defined to be.
That's a good intuitive start.Quote: 1call2manyIt sounds like you are saying what I thought I already knew that the further you care to travel along the series, the tinier the difference between sum and limit? Or no matter how small a number we think of we can add more terms to get a little closer and hence a smaller difference?
At infinity we have reached the limit, however, using English for these discussions is problematic because it isn't specific enough. Don't think of adding the terms ones at a time. Imagine they are weights already sitting on a scale and you are trying to find a weight which counterbalances the other side.Quote: 1call2manyThat says to me we will never reach the limit. ( how could you reach anything with no end to the addition). I notice the Wikipedia link kept using the term arbitrarily close, is arbitrarily close, close enough to say let's just roll with it, it makes all our calculus work, etc.etc.
We do like to be precise. Infinity is a tricky thing, intuition often breaks down out there. Sadly, for math like this you either need to "take our word for it" or be willing to suffer through many semesters of college math so you can prove it yourself.Quote: 1call2manyThere must be more to it, mathematitions like to be precise, arbitrarily close and acts like it's there, does not seem like a compelling reason to believe that it can sum to the limit.
Quote: 1call2manyConsider the series 0.3+ 0.03+ 0.003... Most will agree that it is an infinite series i.e. it has no last term, and continues forever. Most will also agree that there is no term n for which the sum of the series equals exactly 1/3, except for n=infinity. This is where I have the issue. I know that "when" is not a definable math term but If someone could give me a general idea of when it adds up to exactly 1/3 that would help me tremendously.
For any finite n your (finite) sum equals to
0.3+ 0.03+ 0.003... = sum_n 0.3 * 0.1^n = 0.3 * (1 - 0.1^(n+1)) / (1 - 0.1)
For the infinite sum you take the limit n->infinty of the finite sum. The term on the right hand side 0.1^(n+1) limits to 0, so the infinite sum is 1/3 exactly.
Quote: 1call2many[. The limit gives us that for any tiny number, no matter how small, there exists a number terms that if you add them up the difference between the limit (1/3) and the sum of those terms will be less than that tiny number. Using that definition it makes sense to say that infinite number of terms sums to the limit.
Wikipedia's limit article is good as of my last reading of it
It sounds like you are saying what I thought I already knew that the further you care to travel along the series, the tinier the difference between sum and limit? Or no matter how small a number we think of we can add more terms to get a little closer and hence a smaller difference?
That says to me we will never reach the limit. ( how could you reach anything with no end to the addition). I notice the Wikipedia link kept using the term arbitrarily close, is arbitrarily close, close enough to say let's just roll with it, it makes all our calculus work, etc.etc. There must be more to it, mathematitions like to be precise, arbitrarily close and acts like it's there, does not seem like a compelling reason to believe that it can sum to the limit.
Arbitrarily close actually has a precise meaning. So take a sequence of numbers a_1, a_2, ..., a_n, .... such a sequence converges to L if for every e>0 there exist an N such that for all m>N abs(L-a_m)<e. Where abs(x) means the absolute value of x. Now if we move onto series a series converges if its sequences of partial sums converge. The partial sums of a series are s_n=a_1+a_2+...+a_n where a_i is the ith term in the series.
Quote: TwirdmanArbitrarily close actually has a precise meaning. So take a sequence of numbers a_1, a_2, ..., a_n, .... such a sequence converges to L if for every e>0 there exist an N such that for all m>N abs(L-a_m)<e. Where abs(x) means the absolute value of x. Now if we move onto series a series converges if its sequences of partial sums converge. The partial sums of a series are s_n=a_1+a_2+...+a_n where a_i is the ith term in the series.

The definition that Twirdman is referencing was developed by Karl Weierstrass who finally removed any ambiguity from the "intuitive" concept of limits and continuity. I should warn you that the definition can be a little intimidating for the non-mathematician.
I prefer to think of the simple example of a hypothetical stairs (ignore the nose on each step).
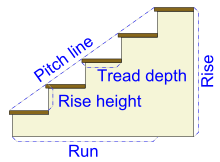
If the rise is 30, and the run is 40, the length of the 5 step rises PLUS the 5 step treads is 70 (ignore the nose). Now increase the number of steps from 5 to 1000 in your mind. The total length of the rises a and treads is still 70. Now increase the number of steps to a billion. The stair begins to approach the limit of a straight line. But we know a straight line is of length 50 by Pythagorean theorem. But the increase in number of steps should not change the total length of the sum of rises and tread lengths (which should be 70).
Wierstrauss formally and mathematically defines the concept of limit so that this kind of fuzzy thinking is exposed. In reality it is incorrect to say that the hypothetical stairs with billions of steps "is approaching" a straight line.
Quote: 1call2manyI just finished reading the .99... Equals or does not equal 1 debate from 2012. What a fascinating read! Well at least for the first half. Being a self proclaimed math hobbiest ( passed high school level math only) I was drawn to ydr11's arguments that .33.. does not accurately represent 1/3 as it is unresolved. Not only do the 3's go on forever but so does the remainder of 1 that causes the next 3,and so on and so on, leaving it in a perpetually unresolved state.
Think of a number as an idea, not as squiggles on paper or pixels on a screen. Infinitely repeating 9s are then obviously an artifact of expressing the idea in base 10. It isn't the number itself that is repeating, it is just another way of expressing it.
The incredible history of infinitesimals and the birth of modern mathematics
Nice explanation of how the concept evolved.
Quote: 24BingoBoth, really. No matter how small a number we can think of, once you've added enough terms, you'll not only be closer, but never be further again, no matter how many more terms you add. For that to be true, the difference has to keep getting smaller and smaller as you add more terms.
Are you saying that at some far off number in the series, I will call it C, it will be such that C+ C.1/3 = C because it is making Absolutely no Progress? Now my 1/3 was the ratio right, I will call it R
So C + CR = AP (absolutely no progress)
You've mad it simple to understand it's CCRAP!
Quote: 1call2manyBoth, really. No matter how small a number we can think of, once you've added enough terms, you'll not only be closer, but never be further again, no matter how many more terms you add. For that to be true, the difference has to keep getting smaller and smaller as you add more terms.
Are you saying that at some far off number in the series, I will call it C, it will be such that C+ C.1/3 = C because it is making Absolutely no Progress? Now my 1/3 was the ratio right, I will call it R
So C + CR = AP (absolutely no progress)
You've mad it simple to understand it's CCRAP!
I have no idea what this is supposed to say. But basically what happens is say I want to get with .1 of 1/3. abs(3.3-1/3)<.1 as is every later term in our partial series so if e was .1 then N=2. Now say I want to get within 1/100000000000000000 of 1/3 there would be some point in the sequence where abs(1/3-s_n)<1/100000000000000000 also for every later term in the sequence abs(1/3-s_m)<1/100000000000000000 if m>n. So all the definition is saying is no matter how precise you want to get there is some point where you are that close and you will forever remain that close.
That does not mean the series is not changing. For instance 3.3 is not the same as 3.33 but 3.3 satisfied one of our initial choices of e. It just means that the series can't move out of a certain bubble.
It sounds like I am meant to believe that the terms get so small that, while they are real positive numbers albeit infinitesimal, they add no value or amount to the total of the series? Extremely small values must then equal zero otherwise adding them would bring the total closer to the limit?
Quote: 1call2manyIt sounds like I am meant to believe that the terms get so small that, while they are real positive numbers albeit infinitesimal, they add no value or amount to the total of the series? Extremely small values must then equal zero otherwise adding them would bring the total closer to the limit?
Of course total of the finite series never approaches 1/3, the "gap" is always positive and remains finite for any number of terms. You are right on that.
You need to learn about limiting values. The *infinite* series is not meant to "add up all terms" together - you can't do that, they are infinitely many, you will never finish doing that. The infinite series is simply defined as the limiting value of the corresponding finite series - whenever this limit exist, the infinite series is defined as this limit.
How to calculate such limits is a different question. But once you accept the finite series is convergent, i.e. has a limit, you can easily understand that this limit is 1/3, and as such the infinite series represents 1/3.
Quote: 1call2manyI have no issue saying an infinite series can be used to represent a limit, I just have trouble with it equalling the limit, which is what I thought people were arguing.
Mathematicians know that (a) the infinite series is not actually equal to the limit, but (b) they are essentially equal, and (c) letting them be equal is very convenient.
It's a zen moment in math when you realize they are not the same, but they are. And then you can sleep at night. I promise.
Infinity is a mathematical construct which does not exist in the physical realm we experience. Large numbers give us hints of what goes on at infinity but never the full glory. I know this phrasing may sound non-secular. In some ways it is.
Remember, that while you are adding infinitesimally small things, you are adding infinitely many of them. Such is the wonder of mathematics that the two infinities "cancel" an we are left with 1/3. Amen.
Quote: 1call2manyWe'll if that is true then I can sleep at night, knowing they are not the same but just so darn close they act like they are. Just best if you don't tell the majority who will endlessly show proofs of why .99... = 1 or .33... = 1/3.
1call,
Referring to your previous post, on how to quote, if you click the "quote" button, then scroll down thru the person's post to the end, you'll see a /q enclosed in brackets. Type after that, and it will look like what I'm writing to you. If you want to isolate something in someone else's post, just highlight and delete the other stuff they wrote, but retain the info in brackets as well as what you're answering so the quote box stays around what they wrote that you want to refer to. Hope that helps.
Quote: dwheatleyMathematicians know that (a) the infinite series is not actually equal to the limit, but (b) they are essentially equal, and (c) letting them be equal is very convenient.
This is absolutely false. The infinite series is equal to the limit, precisely because that is how an infinite series is defined. It's true by definition.
There is no way to sum an infinite series without this definition; it would just be undefined otherwise. 0+0+0+... would also be undefined.
That video was pretty cool indeed. I will meditate on your thought that the two infinities can cancel each other out to be left with a finite number.
thanks I think I have it now I must have deleted the little code at the end when I cut down the quote last time, resulting in my post being in their quote.Quote: beachbumbabs1call,
Referring to your previous post, on how to quote, if you click the "quote" button, then scroll down thru the person's post to the end, you'll see a /q enclosed in brackets. Type after that, and it will look like what I'm writing to you. If you want to isolate something in someone else's post, just highlight and delete the other stuff they wrote, but retain the info in brackets as well as what you're answering so the quote box stays around what they wrote that you want to refer to. Hope that helps.
Quote: AxiomOfChoiceThis is absolutely false. The infinite series is equal to the limit, precisely because that is how an infinite series is defined. It's true by definition.
There is no way to sum an infinite series without this definition; it would just be undefined otherwise. 0+0+0+... would also be undefined.
So in order to find the sum of an infinite series, someone just had to define an infinite series to be equal to the limit, and presto we have the answer?
Quote: 1call2manySo in order to find the sum of an infinite series, someone just had to define an infinite series to be equal to the limit, and presto we have the answer?
Yup.
That's how everything works in math.
Quote: AxiomOfChoiceYup.
That's how everything works in math.
Lol. I did find a slightly more mathematical proof on Wikipedia that has promise, it goes like this
S = 1 + 1/2 + 1/4....
S/2 =. 1/2 + 1/4 + 1/8...
S - S/2. = 1 so S = 2, the limit.
Sounds fairly good as long as the sum is a real number that can be manipulated algebraically. How do I know the rules apply?
I will illustrate with a similar proof
S = 9 + 90 + 900...
10S = 90 + 900 + 9000...
S - 10S = 9
-9S = 9
S = -1
This obviously does not work because the sum is not a real number, it's infinite. What if the sum of the infinite series is not calculable and hense not a real number?
Quote: 1call2manyLol. I did find a slightly more mathematical proof on Wikipedia that has promise, it goes like this
S = 1 + 1/2 + 1/4....
S/2 =. 1/2 + 1/4 + 1/8...
S - S/2. = 1 so S = 2, the limit.
I would call this less mathematical.
Don't get me wrong, I use this trick myself sometimes, but it makes the prior assumption that S is defined, which is not always the case (not all infinite sums are defined).
It is also not clear that you can perform that cancellation -- that part is a little bit hand-wavy.
Quote:What if the sum of the infinite series is not calculable and hense not a real number?
Then it is undefined. This is why it is important that the sum is defined as a limit. It is not defined when the limit does not exist.
Quote: 1call2manyLol. I did find a slightly more mathematical proof on Wikipedia that has promise, it goes like this
S = 1 + 1/2 + 1/4....
S/2 =. 1/2 + 1/4 + 1/8...
S - S/2. = 1 so S = 2, the limit.
Sounds fairly good as long as the sum is a real number that can be manipulated algebraically. How do I know the rules apply?
I will illustrate with a similar proof
S = 9 + 90 + 900...
10S = 90 + 900 + 9000...
S - 10S = 9
-9S = 9
S = -1
This obviously does not work because the sum is not a real number, it's infinite. What if the sum of the infinite series is not calculable and hense not a real number?
There are rules for when a series converges. I already gave you the one commonly used which is to look at the sequence of partial sums and see if it converges. If a positive series, series where all terms were positive, converges then you can do manipulation of it to try and find out what it is equal to. You however cannot do manipulation of series which don't converge.
Quote: AxiomOfChoiceThis is absolutely false. The infinite series is equal to the limit, precisely because that is how an infinite series is defined. It's true by definition.
There is no way to sum an infinite series without this definition; it would just be undefined otherwise. 0+0+0+... would also be undefined.
If you want to be stubbornly precise, this is only true under one set of axioms. Just because you subscribe to one axiomatic mathematics language doesn't make it the only correct perspective.
There are other numbering systems where the two don't need to be equal. See for instance, Mathematics: A Very Short Introduction by Gowers.
Quote: dwheatleyIf you want to be stubbornly precise, this is only true under one set of axioms. Just because you subscribe to one axiomatic mathematics language doesn't make it the only correct perspective.
There are other numbering systems where the two don't need to be equal. See for instance, Mathematics: A Very Short Introduction by Gowers.
Yes but it is the standard axiomatic set used. If you chose to use other axiom systems you should mention that when you say it is not true.
The fact is saying that an infinite series doesn't equal its limit because there exist axiom systems where it doesn't is like saying mercury isn't a liquid because above a certain temperature it is a gas. Mercury is a liquid and an infinite series equals its limit unless we specify further exactly what we are talking about.
Quote: dwheatleyIf you want to be stubbornly precise, this is only true under one set of axioms. Just because you subscribe to one axiomatic mathematics language doesn't make it the only correct perspective.
What do you mean by "correct"?
Sure, if you want, you can redefine all the words that we are using, and then you will end up with completely different results. So what? The words still have standard definitions, and, unless you specify otherwise, the assumption is that you are using those standard definitions.
The OP knows they are equal but doesn't truly understand why. The axiomatic answer is 'because we say so'. Very helpful :p
Looking beyond the definitions of series: They're not equal. Until they are. That's when they become equal, when you swallow the red-hot iron ball.
Quote: dwheatleyMy point (in a roundabout way) is that falling back on the definition of an infinite series does nothing to help the OP resolve his difficulty. Look at the original question: "When does a series with an infinite number of terms equal the thing it converges to?"
The OP knows they are equal but doesn't truly understand why. The axiomatic answer is 'because we say so'. Very helpful :p
But that actually is the only reason that they are equal. It's because that's how it was defined.
The point is, there is no way to extend summation to the infinite case without defining it a certain way. One cannot logically deduce that the sum is equal to the limit -- that's why it had to be defined that way. It's the same reason that there is an axiom of infinity in set theory -- the existence of infinite sets cannot be deduced without it (assuming that the other axioms are consistent, that is. If they are inconsistent, every statement can be deduced).
Quote: 1call2manyI have no issue saying an infinite series can be used to represent a limit, I just have trouble with it equalling the limit, which is what I thought people were arguing. The sum of an infinite series formula implies it can reach the limit when it removes r^infinity as equalling zero when 1 > r > -1, and r does not equal zero? Shouldn't that never reach zero e.g. 1/2^infinity is itself a series 1/2, 1/4, 1/8... If 1/2^ infinity equals zero we could reverse it and say the infinity root of zero equals 1/2? Ironically, if true, it would be able to equal any number between -1 and 1 except zero, which actually can multiply with itself to get zero!
I was never good at advanced math, but was excellent at the basic stuff. Fought thru a basic calc course in college just to get a little understanding. This is how I thought of it as an 8th grade layman.
What is 1 minus .99999 infinitely repeating? .0000000 infinitely repeating, the one appears only at the end of infinity. Although technically incorrect reasoning, maybe this would be helpful conceptually.
I can't speak for all mathematicians. But I used to have a friend who was great at math. He didn't seem to realize that some of us are really good at arithmetic and basic algebra. Not that these topics are exactly difficult, but some us can do it really quick. But then you give us problems that the average person can get thru, and we do about as poorly as people who cannot read. We have to conceptualize everything in arithmetic form, we can't go much beyond. Lack of spatial reasoning skills I suppose.
Quote: SonuvabishI can't speak for all mathematicians. But I used to have a friend who was great at math. He didn't seem to realize that some of us are really good at arithmetic and basic algebra. Not that these topics are exactly difficult, but some us can do it really quick. But then you give us problems that the average person can get thru, and we do about as poorly as people who cannot read. We have to conceptualize everything in arithmetic form, we can't go much beyond. Lack of spatial reasoning skills I suppose.
I'm horrible at spatial reasoning but have absolutely no problem with abstract algebra. The two are completely different skills (at least, they are for me).
Quote: MangoJOf course total of the finite series never approaches 1/3, the "gap" is always positive and remains finite for any number of terms. You are right on that.
If you are having trouble with some of these concepts, bear in mind that they have spawned thousands of pages of philosophical discussion and quite a lot of religious text over the centuries. The normal starting point would be one of the most complicated works of Plato, Παρμενίδης .
Quote: SonuvabishI was never good at advanced math, but was excellent at the basic stuff. Fought thru a basic calc course in college just to get a little understanding. This is how I thought of it as an 8th grade layman.
What is 1 minus .99999 infinitely repeating? .0000000 infinitely repeating, the one appears only at the end of infinity. Although technically incorrect reasoning, maybe this would be helpful conceptually.
e.
That kind of helps but again we have to disregard the 1 that should be at the end but can't be because there is no end. This is especially difficult because it's that pesky remainder of one that causes the nines to go on forever in the first place. The nines cannot go on forever without that remainder one which is there by long division definition. To treat .99... As a real number or as having an exact value is to ignor that remainder of one that keeps the nines chugging on forever.
Quote: AxiomOfChoiceBut that actually is the only reason that they are equal. It's because that's how it was defined.
The point is, there is no way to extend summation to the infinite case without defining it a certain way. One cannot logically deduce that the sum is equal to the limit -- that's why it had to be defined that way.
I can understand this, but I can't understand why so many obviously intelligent people would bother to argue with me that an exact sum can be found, if it is only because we define it to be found?
Quote: 1call2manyI can understand this, but I can't understand why so many obviously intelligent people would bother to argue with me that an exact sum can be found, if it is only because we define it to be found?
What are you trying to get people to say? It seems like you are not hearing what you want to hear, so you are arguing about it. Things would go faster if you would just say what you want to hear for an answer.
You could also try reading this: http://en.m.wikipedia.org/wiki/Series_(mathematics)
Quote: Dalex64What are you trying to get people to say? It seems like you are not hearing what you want to hear, so you are arguing about it. Things would go faster if you would just say what you want to hear for an answer.
You could also try reading this: http://en.m.wikipedia.org/wiki/Series_(mathematics)
I've heard what I want to hear and are therefore done. I heard that the sum of an infinite series is impossible to calculate, but because we know the total approaches the limit as the number of terms increase, and that it is mathematically useful to be able to do. We have defined the sum of an infinite series to be the limit. Therefore it is!
Quote: 1call2manyI can understand this, but I can't understand why so many obviously intelligent people would bother to argue with me that an exact sum can be found, if it is only because we define it to be found?
That is how mathematics is done. Things have to be defined before they can be meaningfully talked about. I mean the truth is that actually holds everywhere you cannot meaningful hold a conversation about horses and horse racing if you don't define what a horse is. Similarly you cannot define what it means for an infinite series to converge or to have a limit and equal that limit unless you define what all those terms mean.
Also depending on philosophical views on mathematics the only way you can say any sum can be found is because it is defined that way. 2+2=4 precisely because that is what we say 2+2 equals. Same for any arbitrary sum. The only issue is intuitively the finite sums make sense to you while the infinite sum doesn't. That is not unusual infinity is an incredibly complex topic and it is basically impossible to visualize the normal way.
Quote: 1call2manyI can understand this, but I can't understand why so many obviously intelligent people would bother to argue with me that an exact sum can be found, if it is only because we define it to be found?
That is why I usually try to stay out of these discussions. Sometimes I am successful, sometimes not so much.
A lot of people feel that it's necessary that mathematics somehow mirrors the real world in some way. This is just silly; the concepts in mathematics go far beyond what could exist in reality. That's why it is so beautiful. I do agree that, for things that do exist in reality, it's better to choose an axiom system that mirrors it as much as possible, but the point is that we will always be able to go further in mathematics than we can in the real world, because the real world contains neither the infinite nor the infinitesimal.
At it's core, all math is is a bunch of arbitrarily defined axioms, and all the things that you can deduce from those axioms. It's just one big logic game.
Furthermore, note that an exact sum can, indeed, be found -- by taking the limit. Anything else is just an attempt to intuitively explain why this makes sense, but I feel that this is a waste of time. Intuitive or not, it's how it's defined, and much of mathematics is counter-intuitive.
Quote: 1call2manyI've heard what I want to hear and are therefore done. I heard that the sum of an infinite series is impossible to calculate, but because we know the total approaches the limit as the number of terms increase, and that it is mathematically useful to be able to do. We have defined the sum of an infinite series to be the limit. Therefore it is!
A lot of calculations that involve 'infinity issues' have real practical applications in all sorts of disciplines from engineering to finance etc.
These 'infinity maths' is not just theoretcial mumbo-jumbo because mathematicans have nothing better to do.
For a example in finance, the valuation of a bond that has no redemption date and pays X% Interest per year. ie pays interest for ever, at infinitum by using an appropriate discount factor Y% (higher then X%) based on its risk. There are simple formulas that accurately calculate this and such formulas taking into account the interest to be paid next years, in 10 years, in 100 years and in a million years. Of course you could use a formula to caculate only the interest for the next 20 years and your figure would be around 99% of the 'infinity' figure.
I am more interested in practical applications of all these math and not some esoteric, theoretical issues or advanced proofs of such formulas.
And the best way to understand a limit is graphical. You put this Series , ie 0.3 , 0.33, 0.333 etc on a graph and you see they convergent to 1/3.
OR in practical terms (not quite sure whether this is strictly mathematically correct), what's the smallest number that is equal or bigger than 0.33333..........
The answer is 1/3.
Math people say 1/3 = 0.33333...........
You might say 1/3 is slighly bigger than 0.33333....... but there is no other number smaller than 1/3 which is still biiger or equal to 0.333333....
Which essentially means that it is equal to 1/3.
But .3 repeating infinitely isn't just essentially 1/3, it is exactly 1/3.
You did say it - there is no number that falls between 1/3 and .333...
.333... Is just another symbolic representation of 1/3
1 divided by 3 represented as an inffinite series of calculations is still exactly one third.
Quote: Dalex64
But .3 repeating infinitely isn't just essentially 1/3, it is exactly 1/3.
Yes, I agree with that.
But what I am saying is that Formal Proofs for these things is for Mathematicians.
For people who use math to solve practical problems are not really interested in these Formal Proofs but just the formulas and an understanding of why this is teh case without going through the rigorous formal proofs.


