complex math problem with dice

.....

Quote: vegas702

This may sound like a really really dumb question but i have a bigger purpose in mind. I can't say much at the moment so I have to be vague. So here goes:

Lets say I want to offer a craps bet where the shooter bets on rolling back to back horn numbers. The player wins or loses when 1 of 2 things happens: back to back horns are thrown & player wins OR a 6 is thrown & player loses. *The only time a 6 does NOT lose is right after the 1st horn is rolled such as: 1-6, 2-6, 11-6, or 12-6. A 6 loses the bet in all other casees.

Figuring out the odds and payout for this isnt too bad, but the next part is what I'm having trouble with. Say I want to have a payout similar to the Fire Bet, something like:

1 back to back horns rolled BEFORE a six: 2 to 1
2 back to back horns rolled BEFORE a six: 20 to 1
3 back to back horns rolled BEFORE a six: 200 to 1

I'm not sure how to do the math on this because the bet is still active if the shooter has thrown back toback horns once, but then throws something like 3, then 6. Since The 6 doesn't lose in this case, i'm getting tripped up trying to account for this when attempting to do the math for this problem.

How do I do the math to figure out a payscale similar to the one above ?

First off, I don't think another firebet style wager should start with "1" because they already have "Hopping bets" that do this.

It sounds to me that you want to add another version of hopping bets to the mix and replace the 7 with a 6. Dealers out there are shaking their heads at this as they continue to read.

1) Example "Yo eleven" if I play 2 C&E that covers all the horn numbers I would get after 1 win I get ($14 +2 wager =$16) after 1 win.
2) If I parley that $16 for a second win I would receive $112 after a back to back win as compared to your 2 to 1 that would pay me $2 and another chance at 20 to 1
(Are you starting to get the picture)
3) If I let that $112 ride for another back to back win, I would then receive $784.00 as compared to your 20 to 1 = $40 and still up to win for that 200:1
(Are you still with me?)
4) If I let that $784 ride for another back to back win I would get $5488.00 as compared to leaving my $2 wager up for a chance to win $800.00

Sorry I don't think I would wager on your idea. It's not up there with the "All Small/All Tall" bet.

Quote: vegas702

Say I want to have a payout similar to the Fire Bet, something like:

1 back to back horns rolled BEFORE a six: 2 to 1
2 back to back horns rolled BEFORE a six: 20 to 1
3 back to back horns rolled BEFORE a six: 200 to 1

I'm not sure how to do the math on this because the bet is still active if the shooter

your table showing all the events and probabilities still have to add up to 1 for all wins and losses.
you could just draw a tree diagram and multiply out all the values on each branch
http://www.mathsisfun.com/data/probability-tree-diagrams.html
but making a table is just as easy in a spreadsheet

for your example
P Horn = 6/11 (p)
P 6 = 5/11 (q)
so your three ways of winning, keeping it simple and not solving your exact example
(not factoring in your 2nd roll Mulligan idea that raises the chance of a win and would lower the payouts for each and increases the number of possible events too)
for one win prob: p*p*q
for two win prob: p*p*p*p*q
and so on
your column of probabilities (all wins and losses) still have to add up to 1

for (possibly) a difficult problem, code and run a sim first so you can see where the values should be
by the sim results (the sim results not being exact).

ultimately, the key is listing all the possible events and their probabilities
all down hill from there

Hope this helps some
Sally

Quote: mustangsally

your table showing all the events and probabilities still have to add up to 1 for all wins and losses.
you could just draw a tree diagram and multiply out all the values on each branch
http://www.mathsisfun.com/data/probability-tree-diagrams.html
but making a table is just as easy in a spreadsheet

for your example
P Horn = 6/11 (p)
P 6 = 5/11 (q)
so your three ways of winning, keeping it simple and not solving your exact example
(not factoring in your 2nd roll Mulligan idea that raises the chance of a win and would lower the payouts for each and increases the number of possible events too)
for one win prob: p*p*q
for two win prob: p*p*p*p*q
and so on
your column of probabilities (all wins and losses) still have to add up to 1

for (possibly) a difficult problem, code and run a sim first so you can see where the values should be
by the sim results (the sim results not being exact).

ultimately, the key is listing all the possible events and their probabilities
all down hill from there

Hope this helps some
Sally

Nice job explaining things Sally.
There are only 2 events we care about rolling a 6 (5/36) and rolling back to back horns(6/36)*(6/36)=(1/36)
probability of back to back horns before a 6 is (1/36)/((1/36)+(5/36)) = 1/6
probability of a 6 before back to back horns is (5/36)/((1/36)+(5/36)) = 5/6

Could you clarify the bet a little?
Here are some examples:
(a) 2, 3, 6 - does the 6 end the bet (with a 2-1 payout) because it wasn't immediately after the first horn number?
(b) 2, 3, 3, 6 - again, does the 6 end the bet or not?
(c) 2, 6, 6 - is the bet lost because the second 6 was not immediately after a horn number?
(d) 2, 6, 12, 6 - does the second 6 end the bet?

Quote: ThatDonGuy

Could you clarify the bet a little?
Here are some examples:
(a) 2, 3, 6 - does the 6 end the bet (with a 2-1 payout) because it wasn't immediately after the first horn number?
(b) 2, 3, 3, 6 - again, does the 6 end the bet or not?
(c) 2, 6, 6 - is the bet lost because the second 6 was not immediately after a horn number?
(d) 2, 6, 12, 6 - does the second 6 end the bet?

My answers for what I understand:
a: yes 2:1 and bet ends
b: 2:1 so far and the 6 does not end the bet
c: yes the second 6 ends the bet
d: the best continues after the 2nd 6.

The bet has 2 steps:
1 - Roll dice
a: roll any number that's not a 2,3,6,11,or 12 : repeat step 1
b: roll a 6: bet loses.
c. roll a 2,3,11, or 12: go to step 2

2 - Roll dice.
a: roll a 2,3,11, or 12 bet wins and continue with step 1
b: roll any number that's not a 2,3,11, or 12 : repeat step 1

Quote: miplet

The bet has 2 steps:
1 - Roll dice
a: roll any number that's not a 2,3,6,11,or 12 : repeat step 1
b: roll a 6: bet loses.
c. roll a 2,3,11, or 12: go to step 2

2 - Roll dice.
a: roll a 2,3,11, or 12 bet wins and continue with step 1
b: roll any number that's not a 2,3,11, or 12 : repeat step 1

In that case, it's a "state" problem. The key to solving these is to pretty much ignore things that don't change the state.

Start off at "initial bet state"
One of five things can happen:
(a) Roll a 6 (probability 5/36) - this changes the state to "bet lost"
(b) Roll two consecutive horn numbers (probability 1/36) - this changes the state to "1 win"
(c) Roll a horn number, then roll something other than a horn number of 6 - this keeps the bet at its current state, so ignore it
(d) Roll something other than a horn number or 6 - again, this keeps the bet at its current state, so ignore it

The probability of losing is 5/36 / (5/36 + 1/36) = 5/6
The probability of getting to the 1 win state is 1/36 / (1/36 + 5/36) = 1/6
As Sally pointed out, notice that the sum of the probabilities is 1.

At the "1 win" state, the same four things can happen as in the initial bet state, except that (a) changes to "bet ends with 1 win" and (b) to the "2 win" state.
The probability of ending at the 1 win state is 1/6 * 5/6 = 5/36.
The probability of getting to the 2 win state is 1/6 * 1/6 = 1/36.
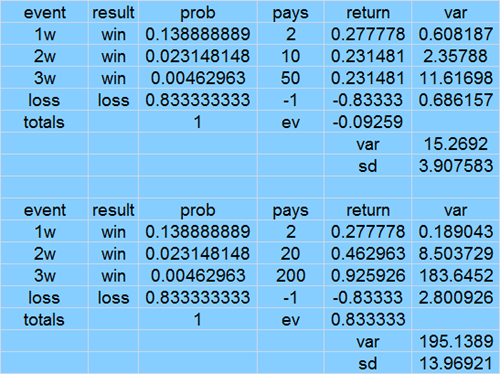
Similarly, the probability of ending at the 2 win state is 1/36 * 5/6 = 1/216, and the probability of reaching the 3 win state (where the bet ends at 200-1) is 1/36 * 1/6 = 1/216.
The final probabilities are:
Loss: 5/6
2-1 win: 5/36
20-1 win: 5/216
200-1 win: 1/216
Once again, these add up to 1.
Notice that the 200-1 payout by itself (EV 200 * 1/216) more than covers the loss (EV = -1 * 5/6 = -180/216).

Quote: ThatDonGuy

Notice that the 200-1 payout by itself (EV 200 * 1/216) more than covers the loss (EV = -1 * 5/6 = -180/216).

nice work
that is why I did not want to solve his exact example, I think it was just an example pulled out of a hat so he could see a method to use to figure out the probabilities so a return table could be made like this
2,10,50 pay table would be nicer for the casino

Sally

.....