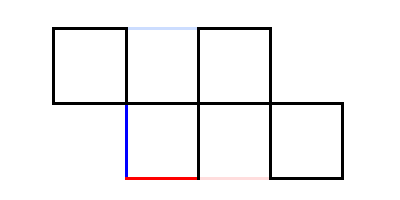
Using unit length toothpicks, construct the diagram whose link is shown below, or continue reading for a textual description which is a horizontal line of three identical squares, using only a single vertical toothpick to delineate them (i.e. don't make double walls). Immediately below, but adjoining the top row, add two more horizontally connected squares, but offset them to the right of the original set by two units. Again, use existing horizontal toothpicks from the bottom of the top row to separate the top row squares from the bottom row squares. You should now have staggered two rows which, together could be bounded by a single 4x2 unit rectangle.
Diagram
The challenge is to modify this configuration to create four identical squares by moving (and/or re-orienting) exactly two toothpicks.
In a lunch time experiment a few years ago, I was one of twenty or so engineers presented with this problem. As expected, some of us "got it" and some of us didn't. What was interesting was that the winners (about a 25% of us) uniformly solved it in under five minutes. The other 75% either gave up after an hour or so, or returned victorious after an exhausting week of trying hundreds of possible combinations.
So here's the lesson: Before you just "dive in" to a problem, try to use all of the available (or derivable) information presented to "design the solution". If you succeed you'll appreciate the value of investing more time in "up front diagnosis" compared to brute force head banging.
Quote: BuzzardWhy struggle at all ? Use a tooth pick for what it is engineered for. Picking teeth !
Um, yeah. Right.
The "no soup" dictum only applies to you (so far).
Quote: skrbornevryminGot it! Take the two toothpicks from upper row upper right hand corner and use them to create a double wall in the center of the remaining rectangles to form four squares with double walls butted against each other. Or just remove them altogether, if that is allowed.
Nope. But this is my fault, not yours.
I should have added that "double walls" are not allowed. Thanks for giving me the chance to clarify that.
Quote: treetopbuddyMy eyes glazed over halfway through reading OP
Thanks for sharing.
But I admit I should used a diagram instead. I'll try to upload one now.
Quote: dblanch256Um, yeah. Right.
The "no soup" dictum only applies to you (so far).
I am having Tomato soup. No need of any toothpick.
Quote: BuzzardWhy struggle at all ? Use a tooth pick for what it is engineered for. Picking teeth !
Wow, an honest to god Belle Starr fan. What are the odds? ;)
Quote: rdw4potusIt's extremely easy to move two toothpicks and get 5 identical squares. I assume that qualifies?
No, sorry. The solution must be exactly four identical squares (and, as mentioned above, no double walls permitted).
Quote: skrbornevryminJust to clarify: Will the solution be exactly and only 4 identical squares or would there be other shapes and/or dimensions involved i.e. 4 squares and a triangle, or 5 squares, or standing a toothpick on end. for example.
The former--four identical squares.
Believe it or not, combined with an observation of the original collection, there is a critical hint lurking within.
Quote: dblanch256The former--four identical squares.
Believe it or not, combined with an observation of the original collection, there is a critical hint lurking within.
I think the problem statement needs more clarification. "Create four identical squares" is not equivalent to "create exactly four identical squares" or "create only four identical squares." It is trivial, for example, to
But it is also easy to
except that's not the intended solution. To continue the thought, if the problem statement had explicitly said
Quote: dblanch256Wow, an honest to god Belle Starr fan. What are the odds? ;)
My daughter let me name her first baby. I named her Belle Starr ! ! !
Quote: JB
By Jove, you've done it. As far as I know, you are the first in this thread to solve it. Congratulations.
Can you describe the "short cut" to which I alluded in the problem statement?
Quote: rudeboyoiToo easy. Took like 20secs.
you take the toothpick from the top of the middle square in the top row. And take the toothpick from the bottom of the first square in the bottom row. Then form a square to the left where the 1st square was in the bottom row.
Yep. Well played. It appears that not everyone even needs a "strategy" for this, although I contend that one exists.
Still, you can't argue with success. Congratulations!
Quote: MathExtremistI think the problem statement needs more clarification. "Create four identical squares" is not equivalent to "create exactly four identical squares" or "create only four identical squares." It is trivial, for example, to
Convert the N pentomino into the P pentomino by moving two toothpicks from an end-square to form a 2x2 section, with a 5th square and a one-toothpick "tail". Of course, any pentomino already has four identical squares, without moving anything.
But it is also easy toConvert the N pentomino into a 4-square shape with either 3+1 or 2+2 adjacent squares, attached diagonally, by "moving" two of the toothpicks back into the box they came from. In the diagram you linked (btw, you should directly post that as an image in your OP), it would be the top and right edges of the rightmost square on the top row, or the left and bottom edges of the leftmost square on the bottom row. Removing either of those pairs of toothpicks leaves four identical squares.
except that's not the intended solution. To continue the thought, if the problem statement had explicitly said"and you must use all your toothpicks." then I think the intended solution (given earlier by JB and others) becomes easier to find. There are 16 toothpicks, so using all of them to create four equal squares requires four unit squares with four sides each. That necessarily means no two squares share an edge, and therefore all of them must be diagonally adjacent (if at all).
Honestly, I think you're being a bit extreme about this, but having read the story about how you got your nom de plume, I can't say I'm too surprised.
Seriously [dude], I'm impressed by your comprehensive critique of the problem statement. I, like you, understand the value of being precise, even though I don't always succeed. I thank you for that.
Finally, you are the first and only person (as far as I know) to reveal the strategy I was hoping others would discover. I can't say it better than you already have so I'll borrow your quote for what I consider to be the crucial initial observation:
There are 16 toothpicks, so using all of them to create four equal squares requires four unit squares with four sides each. That necessarily means no two squares share an edge, and therefore all of them must be diagonally adjacent (if at all).
The above is what I had originally intended when I claimed that one could "design the solution".
Quote: dblanch256Finally, you are the first and only person (as far as I know) to reveal the strategy I was hoping others would discover. I can't say it better than you already have so I'll borrow your quote for what I consider to be the crucial initial observation:
There are 16 toothpicks, so using all of them to create four equal squares requires four unit squares with four sides each. That necessarily means no two squares share an edge, and therefore all of them must be diagonally adjacent (if at all).
The above is what I had originally intended when I claimed that one could "design the solution".
At the highest level of abstraction, the most fundamental rule of problem-solving is "first understand the problem." Knowing what the constraints are (and are not) is often sufficient to indicate the direction of the solution. In that regard, this problem is almost the opposite of the famous 9-points problem:
Without lifting your pencil from paper, use four line segments to connect all nine points in the following diagram

Quote: dblanch256Am I allowed to extend any of my line segments beyond the boundary formed by the outer dots?
The problem statement didn't specify any such restriction or boundary. That is, of course, the fundamental realization that allows a possible solution. (The problem is not solvable if you do not extend any segment beyond the boundary.)
(1) I'd start at the top left dot [1] and draw a line due East extending one dot's distance beyond the top right dot (covering dots 1,2,3).
(2) Then I'd continue on a SW course to a point one dot below the lower left hand dot (covering dots 6,8).
(3) Then I'd head North back to my starting point (covering dots 7,4,1).
(4) Finally I'd move on a SE course ending on lower right hand dot (covering dots 5,9).
Quote: rudeboyoiToo easy. Took like 20secs.
you take the toothpick from the top of the middle square in the top row. And take the toothpick from the bottom of the first square in the bottom row. Then form a square to the left where the 1st square was in the bottom row.
Good work, but "Fasten your seatbelts, <the next few problems> are gonna be a bumpy ride".


