Dealer Bust Pecentage

Hello,

I have never seen any information published regarding.....

What % of BJ player wins come from a dealer bust. I would like to know what the simulatiins show. Is the % consistant fron one sim to the other? How much effect does shoe size and hitting on soft 17 have on the %.

Any information available of this topic?

This is not hard to calculate. Overall, dealer busts 30% of the time, while player 16%, so player does not bust 84%. Therefore, 30% x 84% = 25% of the time player wins on a dealer bust.

Also, player wins 42% of the time; therefore, 25% / 42% = 60% of the player’s wins come from a dealer bust.

However, this calculation does not include correlation between player and dealer. I’d like to hear what other people would say about this.

Quote: Lukes123

Hello,

I have never seen any information published regarding.....

What % of BJ player wins come from a dealer bust. I would like to know what the simulatiins show. Is the % consistant fron one sim to the other? How much effect does shoe size and hitting on soft 17 have on the %.

Any information available of this topic?
link to original post

Lukes123,

I ran a 400-million-round CVData sim for a heads-up BS player on a 6D, H17, DAS game with 75% penetration.

Here is a graph that shows what percentage of the hands played were won by a dealer bust as a function of the HiLo TC:


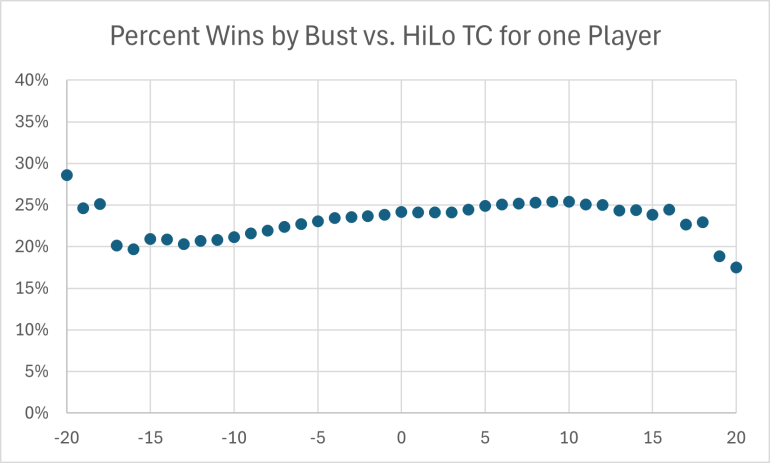
Overall, 24.023% of the hands won PLAYED by the player came as a result of the dealer busting. resulted in a dealer bust.

What other situations would you like to see?

Dog Hand

Edited to correct the meaning of the percentage.

I think you mean 24.03% of all hands not of hands won by player.

Quote: unJon

I think you mean 24.03% of all hands not of hands won by player.
link to original post

unJon,

Oops! You are correct. I shall edit my post.

Now that I have reread the original question, I'll have to rerun the sim.

Dog Hand

Thanks for the reply Dog Hand.

So the question is....Of all hands won by player, what % are won because dealer busted. And, how does shoe size and the Hit vs Stand on soft 17 rule affect this %. And finally, does this % remain consistent if the SIM is run multiple times.

I like the chart you provided. It has me wondering how the various counts affects the percentage of dealer busts.

Any information you provide is much appreciated.

Ok, I ran another sim to see what percentage of the player's hands are wins as a function of the HiLo TC, and then combined that data with the previous sim results to determine what percentage of the player's wins are due to the dealer busting. Here is the combined graph:



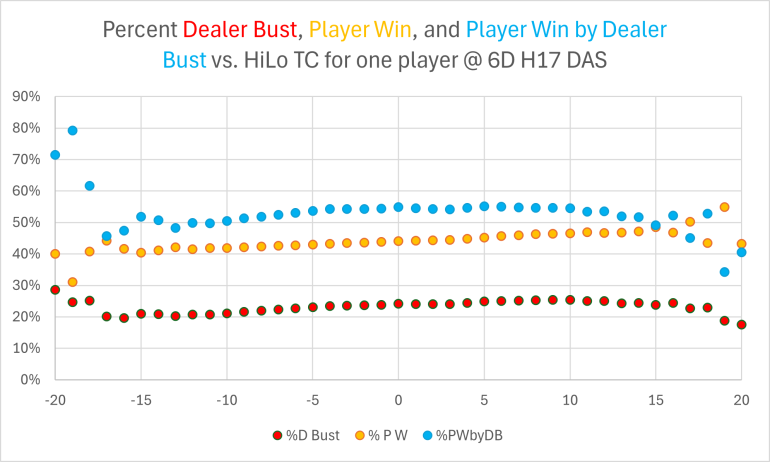
Since the PW% and DB% come from different sims, the values at TC's far from zero have some discrepancies, so I would recommend concentrating on the range -10 <= TC <= +10, which accounts for over 99.9% of the rounds.

The overall values are these:

Dealer Bust % = 24.02%
Player Win % = 44.02%
Player Win by Dealer Bust % = 24.02%/44.02% = 54.57%

If you have CVData, I can post a primer on how to generate these values yourself; if you don't have CVData, then buy it and ... ;-)

Hope this helps!

Dog Hand

Quote: DogHand

Ok, I ran another sim to see what percentage of the player's hands are wins as a function of the HiLo TC, and then combined that data with the previous sim results to determine what percentage of the player's wins are due to the dealer busting. Here is the combined graph:link=/forum/questions-and-answers/gambling/39802-dealer-bust-pecentage/#post946372]link to original post

RPM (count the 9 instead of the ace) correlates a little better to player wins, as well as dealer busts. That's useful for some things.

Hi, your sim result of Player Win % = 44.02% is exceptionally higher than most reported numbers. However, this could be due to several different definitions.

It looks like you used the US rules of dealer peeking for Blackjack and no player surrender. For the US rules, the dealer’s overall bust rate should be about 30%, which excludes the dealer Blackjack hands. For European rules, the dealer’s bust rate should be about 28.6%.

So, how is this 44.02% player win defined? Does it exclude the dealer Blackjack hands?

Thanks a lot for this information. I have to say, I would have thought the % of wins by dealer bust would have been a lot higher. Also that the bust % would have increased at a greater rate with higher counts.

Currently checking out both CVCS and CVData.

Cheers!

Quote: aceside

Hi, your sim result of Player Win % = 44.02% is exceptionally higher than most reported numbers. However, this could be due to several different definitions.

It looks like you used the US rules of dealer peeking for Blackjack and no player surrender. For the US rules, the dealer’s overall bust rate should be about 30%, which excludes the dealer Blackjack hands. For European rules, the dealer’s bust rate should be about 28.6%.

So, how is this 44.02% player win defined? Does it exclude the dealer Blackjack hands?
link to original post

aceside,

Dealer BJ's are not treated differently: the player loses the hand unless he also has a BJ, in which case he pushes.

I believe the difference between my 44% player win and the "usual" 42% is due to splits: I treated each split as a separate hand. Thus, if a player splits to four hands and wins all, I counted that as 4 wins. The "usual" 42% result is actually 42% of the rounds, so in the above case it would be counted as 1 win, since the player won one round.

The lower dealer bust percentage is due to the heads-up situation: if the player busts or has a BJ, the dealer does not have a chance to bust. If the table were full, the dealer would have to play out her hand almost every round and so would bust more often than in my sim.

Note I ran the sim as heads-up one hand to enable me to tally the correct data easily. For example, let's assume we add another player at 3rd base. If our player gets a BJ, 3rd base stands pat, and the dealer busts, our player did NOT win because the dealer busted: he won by having an untied BJ... But without some tricky work-arounds, the stats would make us think the player won because of the dealer bust.

Hope this helps!

Dog Hand

This is excellent! The ultimate goal here to identify the situations where dealer busts more often using a more powerful count. Just as AutomaticMonkey suggests above, to better correlate the dealer bust rate to the count, it’s probably better to count 9’s as a tag +1 but Aces as a tag 0.

If it’s possible, please help investigate this proposal.

I hate to necro (or whatever they call it here, dead thread reviving) but this is something I looked into for a bit while considering a counting system for the easy blackjack game by pragmatic. As such I had a pretty similar program which I tweaked slightly to hopefully bring a little closure to this thread.


Shoe: 8-deck shoe composition
Baseline Bust Probability: 0.28159285
Effect of Removal:

Card	ΔBustProb
2	-0.00007281
3	-0.00002885
4	0.00001336
5	0.00005117
6	-0.00024233
7	0.00027004
8	0.00009437
9	-0.00008754
10	-0.00025922
A	0.00103175

Shoe: 8-deck shoe composition
Baseline Bust Probability: 0.28541892
Effect of Removal:
[/row

Card	ΔBustProb
2	-0.00006118
3	-0.00001174
4	0.00003428
5	0.00006315
6	-0.00030606
7	0.00027929
8	0.00009841
9	-0.00008843
10	-0.00023662
A	0.00093073

I have to admit though that my numbers do not completely line up with those produced by Michael Shackleford in his article on the bust sidebet though they are within what I consider to be reasonable error (mine was brute-forced and not solved with any simulation due to the simplicity of the easy blackjack game, possibly they are slightly off since mine only considers the dealer). The results were concerning to me as my initial assumption was that 6's would be a major benefit to the dealer's bust chance, but this was not the case. It seems that if someone wanted to create an actual counting system for dealer bust % they would want to focus pretty much exclusively on A's and 7's (positive) and 10's and 6's (negative) though id consider the effect to be reasonably negligible. If I could I would add the program I use for this calculation but I do not want to bog down this already convoluted reply.

If you have any gripes with my reply please let me know as I am a beginner when it comes to gambling math. I strictly followed a guide I found from Elliot Jacobson's youtube channel :)

I briefly looked in your two result tables and found something interesting. The EOR values are positive for these cards (4, 5, 7, 8, A) but negative for (2, 3, 6, 9, T). This is totally random, so the result is not good for card counting.

Is it possible you do the same research on a fixed dealer upcard of 6? This is where most bust side bets are based on.

Also, please extend the same research to the dealer upcards of 5 and 4.

Additionally, it’s a lot easier to count a 6-deck than an 8-deck. Just for your information.

I saw the Canadian Counter Girls stop at a casino with this side bet. They didn't bet it at all. The table limit was $300 and they were betting 2, sometimes 3 spots.
A 3 Card dealer bust-out paid 1:1, and a 4 card paid 2:1. There was a max payout of $10K on this bet, so that'd mean a max bet of $40 paying 250:1.
I'm sure other tables with higher max bets would have higher payouts like $25K for a $100 max bet or $50K for a $200 max bet. Since they are under the 300:1 level, there'd be no tax forms.

Blackjack Side Bet - The Buster Bet


The Wizard has a page of calculations and payouts for this bet.
https://wizardofodds.com/games/blackjack/side-bets/buster-blackjack/

Is it possible you do the same research on a fixed dealer upcard of 6? This is where most bust side bets are based on.

Also, please extend the same research to the dealer upcards of 5 and 4.

Yes, ill look into it. I think this will be much more effective then trying to count from prior to dealt cards, high cards aside from ace should be much more clearly beneficial

Shoe after dealing up-card: { '2': 24, '3': 24, '4': 24, '5': 24, '6': 23, '7': 24, '8': 24, '9': 24, '10': 96, '11': 24 }
Baseline Bust Probability: 0.42307899

Card	ΔBustProb
2	0.00133104
3	0.00151332
4	0.00168146
5	0.00183859
6	-0.00008314
7	-0.00046230
8	-0.00079927
9	-0.00110599
10	-0.00151342
11	0.00214644

Shoe after dealing up-card: { '2': 24, '3': 24, '4': 24, '5': 23, '6': 24, '7': 24, '8': 24, '9': 24, '10': 96, '11': 24 }
Baseline Bust Probability: 0.41826768

Card	ΔBustProb
2	0.00130157
3	0.00151127
4	0.00170641
5	0.00188502
6	0.00154782
7	-0.00041159
8	-0.00081959
9	-0.00118415
10	-0.00151422
11	0.00059287

Shoe after dealing up-card: { '2': 24, '3': 24, '4': 23, '5': 24, '6': 24, '7': 24, '8': 24, '9': 24, '10': 96, '11': 24 }
Baseline Bust Probability: 0.39601195

Card	ΔBustProb
2	0.00018756
3	0.00134365
4	0.00156116
5	0.00175407
6	0.00152012
7	0.00118321
8	-0.00076228
9	-0.00117286
10	-0.00154639
11	0.00064463

Far more countable of course. This time I went 6 deck since that seems common in a real casino.

I'm realizing now that previously I was thinking about the effect of removal differently than I should be, a negative effect of removal means more would be beneficial while a positive means it wouldn't. If it was the other way this data would not work at all.

This is assuming the typical "if the dealer busts you win" sort of bet and not the bit more complicated buster blackjack side-bet, which I assume is from the start and a bit more complicated to calculate.

Fantastic! It is countable now. One more thing, the S-17 games are a rarity nowadays. Most games are H-17, I saw.

Luckily this is just a simple settings change, here's what I get for that


Shoe after dealing up-card: { '2': 24, '3': 24, '4': 24, '5': 24, '6': 23, '7': 24, '8': 24, '9': 24, '10': 96, '11': 24 }
Baseline Bust Probability: 0.43940715

Card	ΔBustProb
2	0.00146259
3	0.00165747
4	0.00183743
5	0.00188492
6	-0.00007194
7	-0.00048370
8	-0.00085025
9	-0.00118367
10	-0.00145737
11	0.00157982

Shoe after dealing up-card: { '2': 24, '3': 24, '4': 24, '5': 23, '6': 24, '7': 24, '8': 24, '9': 24, '10': 96, '11': 24 }
Baseline Bust Probability: 0.41953042

Card	ΔBustProb
2	0.00131585
3	0.00152652
4	0.00172262
5	0.00189270
6	0.00155278
7	-0.00040915
8	-0.00081944
9	-0.00118618
10	-0.00150578
11	0.00050203

Shoe after dealing up-card: { '2': 24, '3': 24, '4': 23, '5': 24, '6': 24, '7': 24, '8': 24, '9': 24, '10': 96, '11': 24 }
Baseline Bust Probability: 0.39865227

Card	ΔBustProb
2	0.00011058
3	0.00137582
4	0.00159531
5	0.00177067
6	0.00153099
7	0.00118882
8	-0.00076144
9	-0.00117656
10	-0.00152845
11	0.00055374

Seems to be the same aside from being more significant, I'd have to assume its a different pay table based on them having that preference.