same goes for splitting every pairs.
so far from what I gather, the optimal strategy for this game is essentially to do the opposite (when in possession of high multiplier) of the optimal strategy for normal BJ?
Isn't that the marketing genius of it? They make a game that looks like BlackJack, plays like blackjack and entices the player to play BlackJack strategy: Thus maximising the Hold. Devious beggars!Quote: JDawG888so far from what I gather, the optimal strategy for this game is essentially to do the opposite (when in possession of high multiplier) of the optimal strategy for normal BJ?
link to original post
Their strategy pages were a very generous gesture, and I do hope we can make them player usable and attack the game, especially if there's a better strategy that might offer an advantage.
Since the game is online, some sort of interactive digital strategy assistant would be handy. Probably against their rules, though.
Notes
1) Yes, it is complicated, but this was the simplest way I could find to show it.
2) I want to emphasize, that the strategy for split hands is different. I have an idea how to show it and will present that in a little while.
3. I have tried to accurately to present this, but inevitably I may have made a mistake somewhere.
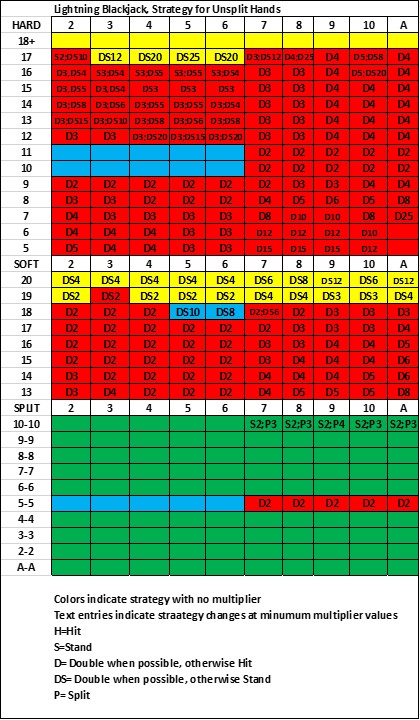
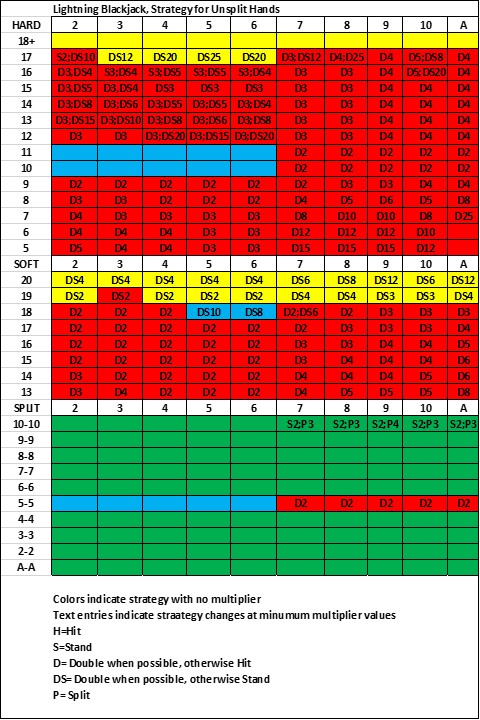
So, for example, at Hard 14 versus 4, the optimal strategy is:
Hit with No multiplier, (and with multiplier = 2)
With multiplier 3+: Double when possible otherwise Hit
Except, with Multipler 5+: Double when Possible otherwise Stand
In Lightning BJ, you may only HIt or Stand on a Split Hand. Remember that Double After Split and Resplitting are not allowed in Lightning Blackjack. These limitations in the player's options do simplify the analysis and presentation of the optimal strategy for playing split hands. On the first hand after a split, according to Evolutionary's published Strategy, it does not matter whether you have initially split Tens or Nines or Sixes or Twos. - for the first split hand strategy depends only on the active multiplier and whether you have made a total of hard 12 -20 or a soft 13-20 after initially hitting your first split card. (Obviously, the player should hit any hand 11 or below. )
So in the above table, the columns correspond to the dealer's up card in the usual way.. However the rows correspond to the value of the active multiplier, ranging from No Multiplier, to the possible multiplier values in the range of 2x to 25x. And the entries in the table are the stop points for hitting.
Example: For a dealer upcard of 5 and an active multiplier of 4x, the table entry is H13, S19 which means that you should hit until you have made a Hard 13 or a soft 19.
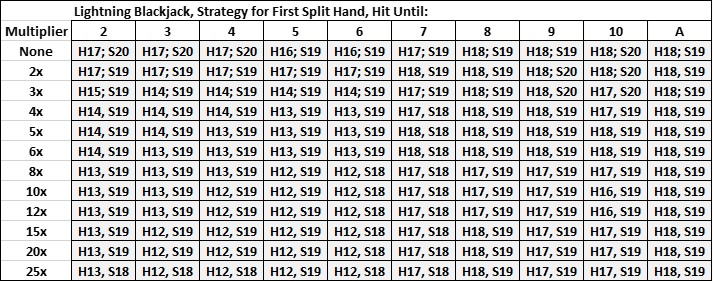
Note that the strategy for the 2nd split hand is very different than this, because it will depend upon the outcome that was achieved in the first split hand. It will also depend upon the multiplier and the dealer's upcard, which makes it challenging to format and present in an intelligible way. I will try to present this strategy as best as I can later today in a subsequent post.
Quote: gordonm888Here is the strategy for the First Split Hand for Evolutionary's Lightning BJ game.
In Lightning BJ, you may only HIt or Stand on a Split Hand. Remember that Double After Split and Resplitting are not allowed in Lightning Blackjack. These limitations in the player's options do simplify the analysis and presentation of the optimal strategy for playing split hands. On the first hand after a split, according to Evolutionary's published Strategy, it does not matter whether you have initially split Tens or Nines or Sixes or Twos. - for the first split hand strategy depends only on the active multiplier and whether you have made a total of hard 12 -20 or a soft 13-20 after initially hitting your first split card. (Obviously, the player should hit any hand 11 or below. )
So in the above table, the columns correspond to the dealer's up card in the usual way.. However the rows correspond to the value of the active multiplier, ranging from No Multiplier, to the possible multiplier values in the range of 2x to 25x. And the entries in the table are the stop points for hitting.
Example: For a dealer upcard of 5 and an active multiplier of 4x, the table entry is H13, S19 which means that you should hit until you have made a Hard 13 or a soft 19.
Note that the strategy for the 2nd split hand is very different than this, because it will depend upon the outcome that was achieved in the first split hand. It will also depend upon the multiplier and the dealer's upcard, which makes it challenging to format and present in an intelligible way. I will try to present this strategy as best as I can later today in a subsequent post.
link to original post
What a great strategy, I hope AP can use your strategy to get RTP 99.56(or even more than 100 with certain promotions !)
Quote: ssho88[
What a great strategy, I hope AP can use your strategy to get RTP 99.56(or even more than 100 with certain promotions !)
link to original post
I'm not sure that this strategy (which is a reformatting of Evolutionary's posted strategy) is the theoretically optimum strategy for split hands. I think the person who developed this strategy may have missed something. But even if they did miss something, the extra EV one might gain from better optimization of decisions on split hands is probably incredibly small.
Quote: gordonm888Quote: ssho88[
What a great strategy, I hope AP can use your strategy to get RTP 99.56(or even more than 100 with certain promotions !)
link to original post
I'm not sure that this strategy (which is a reformatting of Evolutionary's posted strategy) is the theoretically optimum strategy for split hands. I think the person who developed this strategy may have missed something. But even if they did miss something, the extra EV one might gain from better optimization of decisions on split hands is probably incredibly small.
link to original post
I've just been comparing some of the strategy charts and have noticed some subtle differences between the multiplier selections. I'm just wondering if you've accounted for that in the work you've done so far.
There is, for example, five strategy charts for the 2x multiplier, with each one potentially different depending on which "set" of multipliers, are in play.
I'd hate to think that you've done this work and maybe hadn't spotted that. The same is true of all multipliers, each one has 5 different versions - which is perhaps why Evolution presented them in the way they have?
Forgive me I haven't cross-referenced what you've done - my eyes just can't take it lol, just thought I'd flag it up to help.
Quote: NeilLCC
I've just been comparing some of the strategy charts and have noticed some subtle differences between the multiplier selections. I'm just wondering if you've accounted for that in the work you've done so far.
There is, for example, five strategy charts for the 2x multiplier, with each one potentially different depending on which "set" of multipliers, are in play.
I'd hate to think that you've done this work and maybe hadn't spotted that. The same is true of all multipliers, each one has 5 different versions - which is perhaps why Evolution presented them in the way they have?
Forgive me I haven't cross-referenced what you've done - my eyes just can't take it lol, just thought I'd flag it up to help.
link to original post
I noticed this too. With no active multiplier, but high potential multiplier, you don't double.
Quote: mipletI noticed this too. With no active multiplier, but high potential multiplier, you don't double.
Yeah, I think this encapsulates the essence of what makes this game -
a) Potentially attractive to gamblers.
b) Difficult to derive the optimal strategy for.
c) Difficult to present that strategy in a way that can be followed.
- There can be a conflict between the goals of 'banking' what is available to be won on the current hand and shooting for the opportunity of winning more on the next hand.
Quote: mipletQuote: NeilLCC
I've just been comparing some of the strategy charts and have noticed some subtle differences between the multiplier selections. I'm just wondering if you've accounted for that in the work you've done so far.
There is, for example, five strategy charts for the 2x multiplier, with each one potentially different depending on which "set" of multipliers, are in play.
I'd hate to think that you've done this work and maybe hadn't spotted that. The same is true of all multipliers, each one has 5 different versions - which is perhaps why Evolution presented them in the way they have?
Forgive me I haven't cross-referenced what you've done - my eyes just can't take it lol, just thought I'd flag it up to help.
link to original post
I noticed this too. With no active multiplier, but high potential multiplier, you don't double.
link to original post
The charts I have been supplying in the last two days are not at all connected to any earlier charts that charliepatrick, chesterdog or I have presented, They are a complete restructuring and reformatting of the evolutionary strategy presented here: Evolutionary Strategy and its taken me hours to accomplish this.
I don't understand what you mean by "5 different strategy charts for each multiplier." The chart are organized by Hard hands, Soft Hands, Pairs, and First split hand, so yes, each chart accounts for the different possible multipliers. Are those the "5 charts" that you are referring to?
Miplet, I agree with your statement but don't understand the issue you are raising. The only No Multiplier doubles I show on my tables are Double 10,11 vs 2-7 and Double S18 vs 5,6. Those are certainly reasonable doubles, aren't they?
Quote: gordonm888Quote: mipletQuote: NeilLCC
I've just been comparing some of the strategy charts and have noticed some subtle differences between the multiplier selections. I'm just wondering if you've accounted for that in the work you've done so far.
There is, for example, five strategy charts for the 2x multiplier, with each one potentially different depending on which "set" of multipliers, are in play.
I'd hate to think that you've done this work and maybe hadn't spotted that. The same is true of all multipliers, each one has 5 different versions - which is perhaps why Evolution presented them in the way they have?
Forgive me I haven't cross-referenced what you've done - my eyes just can't take it lol, just thought I'd flag it up to help.
link to original post
I noticed this too. With no active multiplier, but high potential multiplier, you don't double.
link to original post
The charts I have been supplying in the last two days are not at all connected to any earlier charts that charliepatrick, chesterdog or I have presented, They are a complete restructuring and reformatting of the evolutionary strategy presented here: Evolutionary Strategy and its taken me hours to accomplish this.
I don't understand what you mean by "5 different strategy charts for each multiplier." The chart are organized by Hard hands, Soft Hands, Pairs, and First split hand, so yes, each chart accounts for the different possible multipliers. Are those the "5 charts" that you are referring to?
Miplet, I agree with your statement but don't understand the issue you are raising. The only No Multiplier doubles I show on my tables are Double 10,11 vs 2-7 and Double S18 vs 5,6. Those are certainly reasonable doubles, aren't they?
link to original post
https://static.egcdn.com/frontend/fec/ring-test/optimalLightningBlackjackStrategy.html?gameType=lightningscalablebj&lang=en#openMenu
There are 5 different next hand multiplier groups each with their own strategy on your current multiplier.
gordonm888, taking your example -
Quote:
So, for example, at Hard 14 versus 4, the optimal strategy is:
Hit with No multiplier, (and with multiplier = 2)
With multiplier 3+: Double when possible otherwise Hit
Except, with Multipler 5+: Double when Possible otherwise Stand
The Evolution strategy tables actually say the following (if I've managed to transcribe it all correctly!) -
If the current set of multipliers on offer is 2x 2x 3x 4x 5x 6x, then
Hit with No multiplier, (STAND with multiplier = 2)
With multiplier 3+: Double when possible otherwise STAND
If the current set of multipliers on offer is 2x 3x 4x 5x 6x 8x, then
Hit with No multiplier, (Hit with multiplier = 2)
With multiplier 3: Double when possible otherwise HIT
With multiplier 4+: Double when possible otherwise Stand
If the current set of multipliers on offer is 2x 3x 4x 5x 8x 12x, then
Hit with No multiplier, (Hit with multiplier = 2)
With multiplier 3,4: Double when possible otherwise HIT
With multiplier 5+: Double when possible otherwise Stand
If the current set of multipliers on offer is 2x 4x 5x 6x 10x 15x, then
Hit with No multiplier, (Hit with multiplier = 2)
With multiplier 3-6: Double when possible otherwise HIT
With multiplier 8+: Double when possible otherwise Stand
If the current set of multipliers on offer is 2x 5x 6x 8x 12x 20x, then
Hit with No multiplier, (Hit with multiplier = 2)
With multiplier 3-8: Double when possible otherwise HIT
With multiplier 10+: Double when possible otherwise Stand
If the current set of multipliers on offer is 2x 5x 8x 12x 15x 25x, then
Hit with No multiplier, (Hit with multiplier = 2)
With multiplier 3-12: Double when possible otherwise HIT
With multiplier 15+: Double when possible otherwise Stand
Quote: gordonm888Quote: mipletQuote: NeilLCC
I've just been comparing some of the strategy charts and have noticed some subtle differences between the multiplier selections. I'm just wondering if you've accounted for that in the work you've done so far.
There is, for example, five strategy charts for the 2x multiplier, with each one potentially different depending on which "set" of multipliers, are in play.
I'd hate to think that you've done this work and maybe hadn't spotted that. The same is true of all multipliers, each one has 5 different versions - which is perhaps why Evolution presented them in the way they have?
Forgive me I haven't cross-referenced what you've done - my eyes just can't take it lol, just thought I'd flag it up to help.
link to original post
I noticed this too. With no active multiplier, but high potential multiplier, you don't double.
link to original post
The charts I have been supplying in the last two days are not at all connected to any earlier charts that charliepatrick, chesterdog or I have presented, They are a complete restructuring and reformatting of the evolutionary strategy presented here: ml?gameType=lightningscalablebj&lang=en#strategies]Evolutionary Strategy and its taken me hours to accomplish this.
I don't understand what you mean by "5 different strategy charts for each multiplier." The chart are organized by Hard hands, Soft Hands, Pairs, and First split hand, so yes, each chart accounts for the different possible multipliers. Are those the "5 charts" that you are referring to?
Miplet, I agree with your statement but don't understand the issue you are raising. The only No Multiplier doubles I show on my tables are Double 10,11 vs 2-7 and Double S18 vs 5,6. Those are certainly reasonable doubles, aren't they?
link to original post
The link you should work from is one level up from the link you posted. Hit the back arrow at the top to see the rest.
This shows the six different multiplier sequences that can be selected for a game round. If you click on one of them it will reveal a strategy chart for that sequence of multipliers. Each Sequence has its own chart and each is different from the other sequence charts. I thought you might only be looking at one of the sequence charts, which I think is what you have done.
I have done all of my compilation, restructuring and reformatting for one specific multiplier group, namely:
2,3,4,5,8,12 (12-17 = 2x; 18 = 3x; 19 =4x; 20 = 5x; 21 = 8x, and BJ =12 X)
but I was unaware that there are 5 other multiplier groups:
2,2,3,4,5,6
2,3,4,5,6,8
2,4,5,6,10,15
2,5,6,8,12,20
2,5,8,12,15,25
So, the multiplier group I picked was the 3rd highest of 6, but one would need to repeat what I have done for another 5 multiplier groups to get a rigorously correct strategy that would produce the declared House Edge value.
That is absolutely bat-stool crazy. That is nuts. The strategy for any one multiplier group is already far too complicated, but to multiply that complexity by a factor of 6X? What were the game designers trying to achieve?
Quote: gordonm888That is absolutely bat-stool crazy. That is nuts. The strategy for any one multiplier group is already far too complicated, but to multiply that complexity by a factor of 6X? What were the game designers trying to achieve?
I think you are being a bit unfair on the game designers. I'm sure they are trying to appeal to typical gamblers, not to the likes of us, and they might well succeed. The complexity of the strategy is only an issue for people trying to follow it, and they will be very few in number! Its publication was probably mostly as a justification for the stated optimal-play house edge, rather than a guide for players.
They've released other 'Lightning' game variations - roulette, baccarat (and maybe some others), each with some kind of random multipliers applied after the betting closes. I guess this is to appeal to slot-player types who like the excitement of random big payouts (or opportunities for a big payout). E.g., in roulette, everyone who has placed a straight-up bet on one of the numbers that then gets a random multiplier has the thrill of then waiting to see if they are about to win unusually big.
This blackjack variant has the additional 'thrill' of the tension between the two conflicting aims of the game - maximise the payout from this round vs maximise the potential payout from the next round. I think the idea is that naive players should be left in a quandary about whether to hit and hope for a big multiplier in the next round or stand for fear of losing the current round's (multiplied) payout.
Quote: gordonm888Its a way to quote an attractively low house edge for a game, while having it play as 85-95% return to player.
link to original post
Indeed. Not trying to say I approve from a moral perspective. Just that I don't think they have in any way blundered in terms of meeting their likely goals.
The first thing I need to do is work on the splitting strategy, for instance at the lowest level I currently do not have any splitting 4s, so I am guessing it's worth it because of the advantage of having two attempts to get to 21.
Quote: charliepatrickI'm beginning to have another look at this but have worked out that the chances of each "Set" of multipliers cannot be equal (it makes it too advantageous to the player). Unless there are any better indications I'm going to guess the chances are 40%,25%,15%,10%,5%,5%; this gives an average of 2 2.9 4 5.2 7.05 9.95 which is close to the averages the wizard posted (another idea is 50% 15% 12.5% 10% 7.5% 5% which gives similar results). However without the exact ratios one isn't going to be able to derive a proper House Edge unless it happens to come out at exactly their figure!
The first thing I need to do is work on the splitting strategy, for instance at the lowest level I currently do not have any splitting 4s, so I am guessing it's worth it because of the advantage of having two attempts to get to 21.
link to original post
Charlie, no need to work out any strategy, just go to the Evolution Lightning Poker web site and you can find tables of all the strategy for all of the possible situations. The problem is that, given the six sets of multipliers, there are so many thousands of possible situations, that the problem becomes one of mapping the optimal decisions onto whatever structure/framework makes sense for your computational models.
Just for determining how to play the 2nd split 6 of a pair of sixes, you must consider:
12 possible values of active multipliers
6 possible sets of multipliers that you might earn
6 possible categories of outcome for the first split hand (Bust, 12-17, 18, 19, 20, 21)
12 possible totals (12-17, S13-S18) that you might have in your 2nd split hand for which the H/S decision is not fixed.
So that is 12*6*6*12 = 5,184 different possible situations for which one needs to define/know the optimum strategy just to play the second split 6 when dealt a pair of sixes!
Not to mention playing the first split 6 of a pair 66! Or how to draw to a split pair of 10's (TT is a very important hand because this situation occurs frequently). Or playing a S14 vs 14 or a hard 17 vs 8 or any of the >100 "hands" that need to be defined.
Pardon the pun, but I really believe that this game is an evolutionary dead end.
Quote: charliepatrick...Multiplier for this hand is x5
link to original postD: 6 Spl: A2346789X H: 13 (13 13 12 12 11 11) h: 7 (7 7 8 7 7 7[u/]) D: D16 D15 D14 D13 D12 D11 D10 D9 D8 D7 D6 D5 D4 D3 D2 D1 d: d10 d9 d8 d7 d6 d5 d4 d3
For fun I wondered what would happen if there was no value of passing any hand to the next phase, for a regular game it gave the regular strategy and a house edge of 0.792% (this assumed you didn't pay the "Ante"). Using similar logic you get a range of EVs for various multipliers (0.499 for 2x, up to 16.639 for 25x).
Then I plugged those values into the carry forward and, after a quick play around, found if Set 1 thru Set 6 were picked with 50% 20% 12.5% 7.5% 5% 5% I got a House Edge of 0.36% (i.e. payback of 99.63%).
I've yet to work through the strategy to see if it matches.
About splits - I looked at all the splits as on occasions it mattered which cards you had split (for instance splitting 9s might make it easier to get to 19 than splitting 6s). So the H1: and h1: lines give the hit/stand point for pairs of 2 3 4 5 6 7 8 9 X (Note: some of these values are impossible, e.g. you can't really get a soft total where you might hit from splitting 10s or 9s., also you never split 5s.) I'm not sure why I've got more hitting than they have for the first hand, I only checked one case so might revisit this.
These are for set 1.
Parms: ndx:8 m17:0.499345 m18:0.499345 m19:1.089821 m20:1.724817 m21:2.374416 mBJ:3.031365 mIN:0 vow:1 Time:20:46:56:782
D: 1 Spl: A2346789 H: 17 (17 17 17 17 16 16) h: 8 (8 8 8 8 8 8) D: d: H1: 17 17 17 17 17 17 17 17 17 h1: 8 8 8 8 8 8 8 8 8
D: 2 Spl: A2346789 H: 15 (15 16 16 15 13 12) h: 8 (8 8 8 8 7 7) D: D11 D10 d: d8 H1: 16 16 16 16 16 16 16 16 16 h1: 8 8 8 8 8 8 8 8 8
D: 3 Spl: A2346789 H: 15 (15 16 16 14 13 12) h: 8 (8 8 8 8 7 7) D: D11 D10 d: d8 H1: 16 16 16 16 16 16 16 16 16 h1: 8 8 8 8 8 8 8 8 8
D: 4 Spl: A2346789 H: 14 (14 15 15 14 12 11) h: 8 (8 8 8 8 7 7) D: D11 D10 d: d8 d7 H1: 15 15 15 15 16 16 16 16 15 h1: 8 8 8 8 8 8 8 8 8
D: 5 Spl: A2346789 H: 14 (14 15 15 13 12 11) h: 8 (8 8 8 8 7 7) D: D11 D10 D9 d: d8 d7 H1: 15 15 15 15 15 15 15 15 15 h1: 8 8 8 8 8 8 8 8 8
D: 6 Spl: A2346789 H: 14 (14 15 15 13 12 11) h: 8 (8 8 8 8 7 7) D: D11 D10 D9 d: d8 d7 d6 H1: 15 15 15 15 15 15 16 15 15 h1: 8 8 8 8 8 8 8 8 8
D: 7 Spl: A2346789 H: 16 (16 16 16 16 16 16) h: 8 (8 8 8 7 7 7) D: D11 D10 d: H1: 16 16 16 16 16 16 16 16 16 h1: 8 8 8 8 8 8 8 8 7
D: 8 Spl: A2346789 H: 17 (17 17 17 17 16 16) h: 8 (8 8 8 8 8 7) D: d: H1: 17 17 17 17 17 17 17 17 17 h1: 8 8 8 8 8 8 8 8 8
D: 9 Spl: A2346789 H: 17 (17 17 17 17 16 16) h: 8 (8 8 8 8 8 8) D: d: H1: 17 17 17 17 17 17 17 17 17 h1: 8 8 8 8 8 8 8 8 8
D: X Spl: A234789 H: 17 (17 17 17 16 16 16) h: 8 (8 8 8 9 8 8) D: d: H1: 17 17 17 17 17 17 17 17 17 h1: 8 8 8 8 8 8 8 9 9
Overall Result: (Multiplier=0)
Total EV:0.6319449252624262
Parms: ndx:8 m17:0.499345 m18:0.499345 m19:1.089821 m20:1.724817 m21:2.374416 mBJ:3.031365 mIN:2 vow:1 Time:20:46:56:800
D: 1 Spl: A2346789 H: 17 (17 17 17 17 16 16) h: 8 (8 8 8 8 8 8) D: D11 D10 d: H1: 17 17 17 17 17 17 17 17 17 h1: 8 8 8 8 8 8 8 8 8
D: 2 Spl: A2346789 H: 14 (14 15 15 13 12 12) h: 8 (8 8 8 8 7 7) D: D13 D12 D11 D10 D9 D8 d: d9 d8 d7 d6 d5 d4 d3 H1: 15 15 15 15 15 15 15 15 15 h1: 8 8 8 8 8 8 8 8 8
D: 3 Spl: A2346789 H: 14 (14 14 14 13 12 12) h: 8 (8 8 8 8 7 7) D: D13 D12 D11 D10 D9 D8 d: d9 d8 d7 d6 d5 d4 d3 H1: 14 14 14 15 15 15 15 15 14 h1: 8 8 8 8 8 8 8 8 8
D: 4 Spl: A2346789 H: 13 (13 14 14 13 12 11) h: 8 (8 8 8 8 7 7) D: D13 D12 D11 D10 D9 D8 d: d9 d8 d7 d6 d5 d4 d3 H1: 14 14 14 14 14 14 14 14 14 h1: 8 8 8 8 8 8 8 8 8
D: 5 Spl: A2346789 H: 13 (13 13 13 12 11 11) h: 8 (8 8 8 8 7 7) D: D13 D12 D11 D10 D9 D8 D7 d: d9 d8 d7 d6 d5 d4 d3 H1: 13 13 14 14 14 14 14 13 13 h1: 8 8 8 8 8 8 8 8 8
D: 6 Spl: A2346789 H: 13 (13 13 13 12 11 11) h: 8 (8 8 8 8 7 7) D: D13 D12 D11 D10 D9 D8 D7 d: d9 d8 d7 d6 d5 d4 d3 H1: 14 14 14 14 14 14 14 14 13 h1: 8 8 8 8 8 8 8 8 8
D: 7 Spl: A2346789 H: 16 (16 16 16 16 16 16) h: 7 (7 8 8 7 7 7) D: D11 D10 D9 d: d8 d7 d6 H1: 16 16 16 16 16 16 16 16 16 h1: 7 7 7 7 7 7 7 7 7
D: 8 Spl: A2346789 H: 17 (17 17 17 16 16 16) h: 8 (8 8 8 8 8 7) D: D11 D10 D9 d: d8 d7 H1: 17 17 17 17 17 17 17 17 17 h1: 8 8 8 8 8 8 8 8 8
D: 9 Spl: A2346789 H: 17 (17 17 17 16 16 16) h: 8 (8 8 8 8 8 8) D: D11 D10 d: d8 H1: 17 17 17 17 17 17 17 17 17 h1: 8 8 8 8 8 8 8 8 8
D: X Spl: A2346789 H: 16 (16 17 17 16 16 15) h: 8 (8 8 8 8 8 8) D: D11 D10 d: H1: 17 17 17 17 17 17 17 17 17 h1: 8 8 8 8 8 8 8 8 8
Overall Result: (Multiplier=2)
Total EV:1.122538316229665
This is what I referred to in a previous post when I said that I think that Evolution missed something when they developed their strategy for Hit/Stand decisions on split hands.
BTW, analyzng the splitting of a 10-10 pair is where the action is - because a 10-10 pair is roughly 16X more likely to occur than any other pair.
In my local casino they have to be identical ranks - so personally I'm currently assuming there are only 4 ways to get a pair of pictures - however this would probably only affect the EV rather than the strategy.Quote: gordonm888... 10-10 pair is roughly 16X more likely to occur than any other pair.
link to original post
Quote: charliepatrickFor fun I wondered what would happen if there was no value of passing any hand to the next phase, for a regular game it gave the regular strategy and a house edge of 0.792% (this assumed you didn't pay the "Ante"). Using similar logic you get a range of EVs for various multipliers (0.499 for 2x, up to 16.639 for 25x).
Then I plugged those values into the carry forward and, after a quick play around, found if Set 1 thru Set 6 were picked with 50% 20% 12.5% 7.5% 5% 5% I got a House Edge of 0.36% (i.e. payback of 99.63%).
I've yet to work through the strategy to see if it matches.
You're clearly a lot further down the road with this than I am, but I have been giving some thought to how I might go about modifying a CA program to tackle this. In truth, I'm trying to restrain myself from diving in, because -
a) there are other things I am supposed to be doing
b) it looks like a lot of (difficult) work, and
c) there are clearly already some very able people on the case!
What you said in the quoted snippet reminds me of a question I have been pondering - Would an iterative approach work? The idea would be to start by generating a strategy with no value associated with the multiplier being carried forward, use its EVs to generate a modified strategy accounting for the value of the carried forward multiplier, use the EVs of the modified strategy to create yet another modified strategy, and so on until there are no more modifications arising.
Conceptually, the idea is to ask "If I were to apply strategy S0 to the next hand, what is the strategy, S1, I should I apply to the current hand in order to maximise the overall EV?". Then, "If I were to apply S1 on the next hand, what is the strategy S2...." etc.
Does that make sense / sound reasonable?
Also, when it comes to plugging the EVs into the carry forward, I think that it is only the excess EV above what would be won by applying the given strategy under normal BJ rules which should be counted in the carry forward. Otherwise, I think you end up counting this portion of the EV twice, once for each hand. [I have to admit my thoughts on this are all still a little fuzzy, though. I've been going round in circles to some degree.]
Yes I have tried the S0, S1 approach (which is how I got the results I did) but also if I carried on I got to a figure to 4 decimal places with 4 iterations. However it was a player advantage under the worst conditions so I suspect I'm missing a (-1) somewhere for paying the "Ante" to play the next hand.Quote: LC1...What you said in the quoted snippet reminds me of a question I have been pondering - Would an iterative approach work? The idea would be to start by generating a strategy with no value associated with the multiplier being carried forward, use its EVs to generate a modified strategy accounting for the value of the carried forward multiplier, use the EVs of the modified strategy to create yet another modified strategy, and so on until there are no more modifications arising.
Conceptually, the idea is to ask "If I were to apply strategy S0 to the next hand, what is the strategy, S1, I should I apply to the current hand in order to maximise the overall EV?". Then, "If I were to apply S1 on the next hand, what is the strategy S2...." etc.
Does that make sense / sound reasonable?
Also, when it comes to plugging the EVs into the carry forward, I think that it is only the excess EV above what would be won by applying the given strategy under normal BJ rules which should be counted in the carry forward. Otherwise, I think you end up counting this portion of the EV twice, once for each hand...
Using S0 S1 can only be an estimate. That method assumes there is no value of a carry forward for the second hand, so you don't pay the "Ante" and also don't benefit from it - however this possibly means the strategy is slightly different - but it will give a rough idea of the correct EV. (It seems to give a strategy for the first hand close to theirs, so I suspect the carry forward EVs are fairly close and if I added in logic for paying for the "Ante", I might get some convergence.)
btw one reason for using coding is each iteration can create the evs[0]=nnnnn evs[1]=mmmm etc to plug into the next!
Quote: charliepatrick
Using S0 S1 can only be an estimate. That method assumes there is no value of a carry forward for the second hand, so you don't pay the "Ante" and also don't benefit from it - however this possibly means the strategy is slightly different - but it will give a rough idea of the correct EV. (It seems to give a strategy for the first hand close to theirs, so I suspect the carry forward EVs are fairly close and if I added in logic for paying for the "Ante", I might get some convergence.)
Yeah, I glossed over some elements. I was sort of aware that there would be a need for an extra term for the EV arising from the average multiplier won by the second hand (I think I saw you mention this in an earlier post.). And, also, I am wondering if what is actually needed is the EV associated with not just the second hand, but with the average-length of winning streak.
How to correctly account for subsequent main + ante bets in relation to the first hand is a bit confusing to me at the moment. It seems like there is scope to inadvertently count them twice (a bit like the issue I mentioned with the carry-forward EV). With a simulation, you could just divide the total amount won or lost by the total of the initial bets of all the hands played, to get the per-hand EV. With an analytical approach the notional hand is simultaneously playing multiple roles (the 1st, 2nd, and maybe 3rd+ hands).
Quote: LC1-snip-
What you said in the quoted snippet reminds me of a question I have been pondering - Would an iterative approach work? The idea would be to start by generating a strategy with no value associated with the multiplier being carried forward, use its EVs to generate a modified strategy accounting for the value of the carried forward multiplier, use the EVs of the modified strategy to create yet another modified strategy, and so on until there are no more modifications arising.
Conceptually, the idea is to ask "If I were to apply strategy S0 to the next hand, what is the strategy, S1, I should I apply to the current hand in order to maximise the overall EV?". Then, "If I were to apply S1 on the next hand, what is the strategy S2...." etc.
Does that make sense / sound reasonable?
link to original post
The approach you are describing has been used for years to develop poker theory - usually with some AI software together with a looping routine that runs the system several million times. See, for example, Modern Poker Theory by Acevedo.
However, poker decisions involve 'opponent behavior' and thus are not strictly optimizable by probability theory. This game does have the complication that how you play your current hand has implied effects on your effective value in the next hand, but I still think that combinatorial probability methods are the best approach here.
Quote: gordonm888
The approach you are describing has been used for years to develop poker theory - usually with some AI software together with a looping routine that runs the system several million times. See, for example, Modern Poker Theory by Acevedo.
However, poker decisions involve 'opponent behavior' and thus are not strictly optimizable by probability theory. This game does have the complication that how you play your current hand has implied effects on your effective value in the next hand, but I still think that combinatorial probability methods are the best approach here.
link to original post
I think you have misunderstood what I was trying to say. See Charlie's reply to me - the approach I was describing does chiefly consist of combinatorial probability methods, and is essentially the same approach that he is taking.
That being said, I've been thinking some more, and have some new concerns/ideas which I will put in another post...
What I hadn't previously considered is this -
Suppose we play two hands, A then B. We play B with a multiplier which we won in A.
If we assign an EV to B's blackjack bet, based on the multiplier, having also incorporated that EV into hand A ,then surely we have accounted for it twice! (The EV we assign to each hand includes both the winning of the multiplier and the playing of the multiplier.)
So I think we may need to do the following -
Use the sum of the hand EV and the carry-forward EV to rank the strategy decisions, but do not actually update the hand EV to include the carry-forward EV. (That way, the value of a multiplier is only counted when it is actually applied, but we make the right strategy decisions to exploit the multipliers.)
--------------------------------------
And, in general, the fundamental idea would be that only the amounts available to be directly won/lost on the current hand factor into the calculated EV for the hand. The additional EV that stems from carrying forward a multiplier to the next hand (and maybe beyond) only directly impacts the strategy decisions.
Does that make sense?
[Edit: On reflection, I'm not sure it does entirely. Seems like what is missing from the above is the need to determine the frequency with which each multiplier gets won, and use these to weight the contribution of the corresponding strategies to the total EV. Not sure if that can be done.
If I'm right that there is an issue regarding the double counting, maybe there are other, better ways to solve it??]
I'm not sure whether my strategy is being followed (i.e. whether I have transferred all my decisions correctly) but one can see the trend for various hands (the count shows the Multiplier coming in, then the Set of multipliers being carried forward). Typically if the multipliers are higher (i.e. higher set number) you tend to try harder to get towards 21, so the pay-outs for this hand drop a bit.
As I said I don't know the ratio of the set numbers so the bottom line cannot be a realistic indication - as I said earlier I may be hitting the first split hand too much.
The EV of 0.9195... does not take account of having to Pay the "Ante" each round, so the simulation's House Edge is about 8%. So please ignore this value as there's just not enough information!
Parms: ndx:8 sh:1000000 pen:83% Time:23:0:37:564
Count: 0.1 Exp: -0.04148357511305303 Hands: 17885633 Win: 7546539 PayOut: 7546539 Lose: 9500973 Tie: 1611023 BJk: 808316 BJP: 1212474
Count: 0.2 Exp: -0.06315804187202446 Hands: 7154180 Win: 2894951 PayOut: 2894951 Lose: 3832258 Tie: 643154 BJk: 323642 BJP: 485463
Count: 0.3 Exp: -0.06538448375096104 Hands: 4470449 Win: 1797568 PayOut: 1797568 Lose: 2393700 Tie: 401740 BJk: 202556 BJP: 303834
Count: 0.4 Exp: -0.09055808486629695 Hands: 2682549 Win: 1037197 PayOut: 1037197 Lose: 1461976 Tie: 228152 BJk: 121235 BJP: 181852.5
Count: 0.5 Exp: -0.09998456147887608 Hands: 1787736 Win: 662619 PayOut: 662619 Lose: 962949 Tie: 151163 BJk: 81056 BJP: 121584
Count: 0.6 Exp: -0.10212080343273917 Hands: 1788426 Win: 662204 PayOut: 662204 Lose: 966065 Tie: 150007 BJk: 80817 BJP: 121225.5
Count: 2.1 Exp: 0.4632301207167106 Hands: 2437525 Win: 1207089 PayOut: 2414178 Lose: 1505795 Tie: 215777 BJk: 110376 BJP: 220752
Count: 2.2 Exp: 0.43941951279000535 Hands: 975801 Win: 471040 PayOut: 942080 Lose: 601742 Tie: 86023 BJk: 44224 BJP: 88448
Count: 2.3 Exp: 0.431806305236344 Hands: 610445 Win: 294245 PayOut: 588490 Lose: 380440 Tie: 52635 BJk: 27772 BJP: 55544
Count: 2.4 Exp: 0.40027817549601147 Hands: 366675 Win: 166883 PayOut: 333766 Lose: 220268 Tie: 31945 BJk: 16637 BJP: 33274
Count: 2.5 Exp: 0.3634128279716389 Hands: 244419 Win: 103676 PayOut: 207352 Lose: 140869 Tie: 20350 BJk: 11171 BJP: 22342
Count: 2.6 Exp: 0.3335919158088296 Hands: 243636 Win: 96709 PayOut: 193418 Lose: 134511 Tie: 20400 BJk: 11184 BJP: 22368
Count: 3.1 Exp: 1.0417532350981409 Hands: 1626844 Win: 888343 PayOut: 2665029 Lose: 1192049 Tie: 141437 BJk: 73930 BJP: 221790
Count: 3.2 Exp: 1.015029249231196 Hands: 648735 Win: 348600 PayOut: 1045800 Lose: 476262 Tie: 56373 BJk: 29649 BJP: 88947
Count: 3.3 Exp: 1.0098656916694366 Hands: 406155 Win: 218076 PayOut: 654228 Lose: 298588 Tie: 34298 BJk: 18174 BJP: 54522
Count: 3.4 Exp: 0.9793149803477968 Hands: 243993 Win: 128511 PayOut: 385533 Lose: 180001 Tie: 21183 BJk: 11138 BJP: 33414
Count: 3.5 Exp: 0.9563642858462619 Hands: 162367 Win: 82945 PayOut: 248835 Lose: 115816 Tie: 13987 BJk: 7421 BJP: 22263
Count: 3.6 Exp: 0.911240569425602 Hands: 162901 Win: 78957 PayOut: 236871 Lose: 110950 Tie: 13447 BJk: 7507 BJP: 22521
Count: 4.1 Exp: 1.6721937294242444 Hands: 2695223 Win: 1596647 PayOut: 6386588 Lose: 2367973 Tie: 226960 BJk: 122080 BJP: 488320
Count: 4.2 Exp: 1.6536033766549478 Hands: 1077753 Win: 633564 PayOut: 2534256 Lose: 948052 Tie: 89657 BJk: 48993 BJP: 195972
Count: 4.3 Exp: 1.6544075685701038 Hands: 672888 Win: 396035 PayOut: 1584140 Lose: 592317 Tie: 56009 BJk: 30352 BJP: 121408
Count: 4.4 Exp: 1.6220326427813032 Hands: 404990 Win: 234776 PayOut: 939104 Lose: 355721 Tie: 34137 BJk: 18381 BJP: 73524
Count: 4.5 Exp: 1.5964092410221737 Hands: 269191 Win: 149782 PayOut: 599128 Lose: 218377 Tie: 22852 BJk: 12247 BJP: 48988
Count: 4.6 Exp: 1.527822475992733 Hands: 269710 Win: 143357 PayOut: 573428 Lose: 210523 Tie: 22320 BJk: 12291 BJP: 49164
Count: 5.1 Exp: 2.313861643061821 Hands: 2528012 Win: 1513156 PayOut: 7565780 Lose: 2291245 Tie: 212652 BJk: 114987 BJP: 574935
Count: 5.2 Exp: 2.3009359493695962 Hands: 1009670 Win: 607284 PayOut: 3036420 Lose: 942064 Tie: 84117 BJk: 45766 BJP: 228830
Count: 5.3 Exp: 2.293238093583635 Hands: 633209 Win: 380673 PayOut: 1903365 Lose: 594311 Tie: 52251 BJk: 28609 BJP: 143045
Count: 5.4 Exp: 2.301295648154263 Hands: 378575 Win: 227146 PayOut: 1135730 Lose: 349392 Tie: 31676 BJk: 16975 BJP: 84875
Count: 5.5 Exp: 2.2738184694482895 Hands: 252850 Win: 150363 PayOut: 751815 Lose: 233405 Tie: 21054 BJk: 11305 BJP: 56525
Count: 5.6 Exp: 2.2152280885254476 Hands: 252402 Win: 146703 PayOut: 733515 Lose: 231387 Tie: 20899 BJk: 11400 BJP: 57000
Count: 6.1 Exp: 2.9584066605743535 Hands: 1503534 Win: 907376 PayOut: 5444256 Lose: 1403345 Tie: 123874 BJk: 67859 BJP: 407154
Count: 6.2 Exp: 2.951435535079689 Hands: 601901 Win: 364038 PayOut: 2184228 Lose: 568466 Tie: 49729 BJk: 26785 BJP: 160710
Count: 6.3 Exp: 2.939622771903524 Hands: 376218 Win: 226887 PayOut: 1361322 Lose: 355385 Tie: 30897 BJk: 16667 BJP: 100002
Count: 6.4 Exp: 2.9500851350632304 Hands: 225524 Win: 136139 PayOut: 816834 Lose: 213517 Tie: 18474 BJk: 10333 BJP: 61998
Count: 6.5 Exp: 2.929164426924685 Hands: 150687 Win: 90414 PayOut: 542484 Lose: 142011 Tie: 12294 BJk: 6819 BJP: 40914
Count: 6.6 Exp: 2.8766851123408226 Hands: 149990 Win: 88553 PayOut: 531318 Lose: 140326 Tie: 12388 BJk: 6747 BJP: 40482
Count: 8.1 Exp: 4.269767616350093 Hands: 852986 Win: 519161 PayOut: 4153288 Lose: 818324 Tie: 69220 BJk: 38386 BJP: 307088
Count: 8.2 Exp: 4.260744325046842 Hands: 342646 Win: 207903 PayOut: 1663224 Lose: 327561 Tie: 28127 BJk: 15533 BJP: 124264
Count: 8.3 Exp: 4.264874691355132 Hands: 213433 Win: 129588 PayOut: 1036704 Lose: 203383 Tie: 17485 BJk: 9618 BJP: 76944
Count: 8.4 Exp: 4.2623949106011 Hands: 128581 Win: 77999 PayOut: 623992 Lose: 122473 Tie: 10405 BJk: 5818 BJP: 46544
Count: 8.5 Exp: 4.247334605076832 Hands: 85447 Win: 51717 PayOut: 413736 Lose: 82086 Tie: 6908 BJk: 3909 BJP: 31272
Count: 8.6 Exp: 4.235611153329047 Hands: 85535 Win: 51660 PayOut: 413280 Lose: 81475 Tie: 6900 BJk: 3811 BJP: 30488
Count: 10.1 Exp: 5.529431914471668 Hands: 166401 Win: 100553 PayOut: 1005530 Lose: 161517 Tie: 13329 BJk: 7609 BJP: 76090
Count: 10.2 Exp: 5.56565397663023 Hands: 66325 Win: 40297 PayOut: 402970 Lose: 64048 Tie: 5437 BJk: 3022 BJP: 30220
Count: 10.3 Exp: 5.5465503109782555 Hands: 41482 Win: 25161 PayOut: 251610 Lose: 40018 Tie: 3281 BJk: 1849 BJP: 18490
Count: 10.4 Exp: 5.564056152206267 Hands: 24861 Win: 15167 PayOut: 151670 Lose: 23962 Tie: 2005 BJk: 1062 BJP: 10620
Count: 10.5 Exp: 5.5211394844615755 Hands: 16604 Win: 10027 PayOut: 100270 Lose: 16217 Tie: 1343 BJk: 762 BJP: 7620
Count: 10.6 Exp: 5.434637549287231 Hands: 16485 Win: 9789 PayOut: 97890 Lose: 15920 Tie: 1365 BJk: 762 BJP: 7620
Count: 12.1 Exp: 6.889723447356804 Hands: 484754 Win: 295636 PayOut: 3547632 Lose: 471379 Tie: 39019 BJk: 21964 BJP: 263568
Count: 12.2 Exp: 6.92659638057548 Hands: 194064 Win: 118868 PayOut: 1426416 Lose: 188317 Tie: 15463 BJk: 8842 BJP: 106104
Count: 12.3 Exp: 6.900070518936409 Hands: 120535 Win: 73798 PayOut: 885576 Lose: 117356 Tie: 9670 BJk: 5290 BJP: 63480
Count: 12.4 Exp: 6.882513999532202 Hands: 72681 Win: 44364 PayOut: 532368 Lose: 71068 Tie: 5754 BJk: 3244 BJP: 38928
Count: 12.5 Exp: 6.796889276517983 Hands: 48156 Win: 29124 PayOut: 349488 Lose: 47629 Tie: 3686 BJk: 2121 BJP: 25452
Count: 12.6 Exp: 6.847254039997523 Hands: 48453 Win: 29424 PayOut: 353088 Lose: 47202 Tie: 3928 BJk: 2157 BJP: 25884
Count: 15.1 Exp: 8.81284222839327 Hands: 217143 Win: 132045 PayOut: 1980675 Lose: 211823 Tie: 17433 BJk: 9653 BJP: 144795
Count: 15.2 Exp: 8.80559617933367 Hands: 87524 Win: 53195 PayOut: 797925 Lose: 85769 Tie: 7012 BJk: 3903 BJP: 58545
Count: 15.3 Exp: 8.873668611651384 Hands: 53985 Win: 33161 PayOut: 497415 Lose: 52825 Tie: 4306 BJk: 2297 BJP: 34455
Count: 15.4 Exp: 8.833538159026668 Hands: 32548 Win: 19854 PayOut: 297810 Lose: 32061 Tie: 2531 BJk: 1451 BJP: 21765
Count: 15.5 Exp: 8.923147637433352 Hands: 21756 Win: 13345 PayOut: 200175 Lose: 21388 Tie: 1674 BJk: 1023 BJP: 15345
Count: 15.6 Exp: 8.806201907570381 Hands: 21703 Win: 13178 PayOut: 197670 Lose: 21279 Tie: 1670 BJk: 982 BJP: 14730
Count: 20.1 Exp: 12.127636024699989 Hands: 68664 Win: 42052 PayOut: 841040 Lose: 67388 Tie: 5472 BJk: 2954 BJP: 59080
Count: 20.2 Exp: 12.285058905567585 Hands: 27247 Win: 16881 PayOut: 337620 Lose: 26549 Tie: 2193 BJk: 1183 BJP: 23660
Count: 20.3 Exp: 12.334263161018457 Hands: 16849 Win: 10484 PayOut: 209680 Lose: 16380 Tie: 1377 BJk: 726 BJP: 14520
Count: 20.4 Exp: 12.24833071484682 Hands: 10184 Win: 6329 PayOut: 126580 Lose: 10163 Tie: 754 BJk: 416 BJP: 8320
Count: 20.5 Exp: 12.01274074074074 Hands: 6750 Win: 4083 PayOut: 81660 Lose: 6654 Tie: 561 BJk: 304 BJP: 6080
Count: 20.6 Exp: 11.84873949579832 Hands: 6783 Win: 4067 PayOut: 81340 Lose: 6790 Tie: 539 BJk: 291 BJP: 5820
Count: 25.1 Exp: 15.488807775188002 Hands: 68217 Win: 41916 PayOut: 1047900 Lose: 66925 Tie: 5409 BJk: 3025 BJP: 75625
Count: 25.2 Exp: 15.549440879926673 Hands: 27275 Win: 16910 PayOut: 422750 Lose: 26764 Tie: 2162 BJk: 1125 BJP: 28125
Count: 25.3 Exp: 15.404536082474227 Hands: 16975 Win: 10394 PayOut: 259850 Lose: 16733 Tie: 1383 BJk: 735 BJP: 18375
Count: 25.4 Exp: 15.20350535540409 Hands: 10270 Win: 6199 PayOut: 154975 Lose: 10260 Tie: 814 BJk: 457 BJP: 11425
Count: 25.5 Exp: 15.167493434490808 Hands: 6854 Win: 4120 PayOut: 103000 Lose: 6767 Tie: 567 BJk: 309 BJP: 7725
Count: 25.6 Exp: 15.085714285714285 Hands: 6755 Win: 4038 PayOut: 100950 Lose: 6821 Tie: 503 BJk: 311 BJP: 7775
Overall Result: Exp: 0.9195550440431635 Hands: 61067707 Win: 28941532 PayOut: 88288116 Lose: 40226303 Tie: 5315019 BJk: 2762305 BJP: 8093305
Edit: Changing the ratios to 40% 20% 16% 12% 8% 4%, but keeping the same strategy (which might still be close but could be slightly wrong) gives a House Edge of 1%!
Quote: OnceDearQuote: LC1Hi,
Evolution has published their full strategy for the game, accessible via a link in the in-game help text.
[I've been trying to post the link here, but the forum interface keeps removing the bulk of the text when I paste it in, for some reason! In the game help, you can find it in the 'payouts' section - 'Open Strategy in New Window'.]
link to original post
BRILLIANTLY WELL SPOTTED
https://static.egcdn.com/frontend/fec/ring-test/optimalLightningBlackjackStrategy.html?gameType=lightningscalablebj&lang=en#openMenu
It's a little complex and each icon is a link to a busy page.
Something for our maths guys to get their teeth into
link to original post
Seems like that link doesn't work any more. Has anyone captured all the raw information in all those strategy tables, or even a copy of the pages?
Thanks so much for everyone who has done work on this game and has been willing to share.


