March 24th, 2023 at 2:29:34 AM
permalink
.
4 mathematicians have discovered a 2 D shape that does not repeat itself when tiled - see link
tiling that does not have repeating patterns is known as aperiodic tiling
from the article:
"for many years mathematicians have been studying the idea of creating shapes that could be used to create an infinite variety of patterns when tiled"
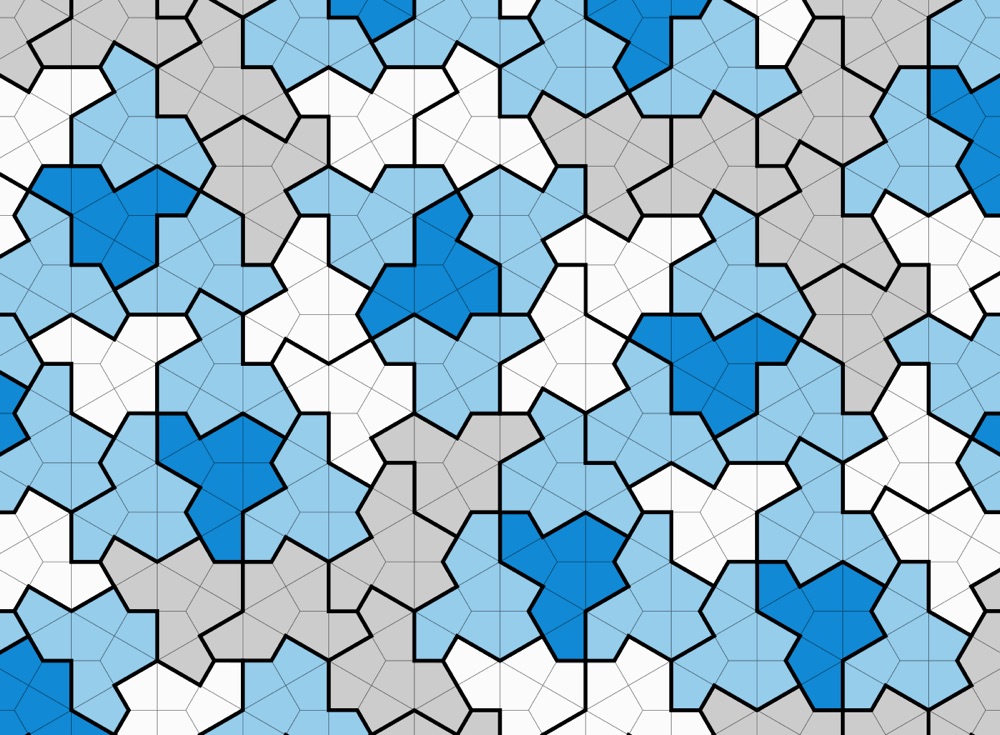
https://phys.org/news/2023-03-geometric-tiled.html
https://kottke.org/23/03/a-potential-major-discovery-an-aperiodic-monotile
.
.
4 mathematicians have discovered a 2 D shape that does not repeat itself when tiled - see link
tiling that does not have repeating patterns is known as aperiodic tiling
from the article:
"for many years mathematicians have been studying the idea of creating shapes that could be used to create an infinite variety of patterns when tiled"

https://phys.org/news/2023-03-geometric-tiled.html
https://kottke.org/23/03/a-potential-major-discovery-an-aperiodic-monotile
.
.
the foolish sayings of a rich man often pass for words of wisdom by the fools around him
March 24th, 2023 at 12:15:58 PM
permalink
Fascinating.
I always feel that 2-dimensional geometry analysis is mostly a warm-up for working a problem in three dimensions. So I did some reading on 3-D tesselation/tiling.
I discovered the Johnson solid.
One of the Johnson solids, called a Schmitt–Conway–Danzer biprism, fills space with a "screw" symmetry and is indeed aperiodic. However it does not fully satisfy the criteria as a solution to the 3-D Einstein problem*.
* The Einstein problem is not named after Albert Einstein; rather Einstein is a German language word and means "one stone."
Johnson solid that fills space with a "screw" symmetry
Seemingly useless info, but I feel richer for knowing this.
I always feel that 2-dimensional geometry analysis is mostly a warm-up for working a problem in three dimensions. So I did some reading on 3-D tesselation/tiling.
I discovered the Johnson solid.
One of the Johnson solids, called a Schmitt–Conway–Danzer biprism, fills space with a "screw" symmetry and is indeed aperiodic. However it does not fully satisfy the criteria as a solution to the 3-D Einstein problem*.
* The Einstein problem is not named after Albert Einstein; rather Einstein is a German language word and means "one stone."
Johnson solid that fills space with a "screw" symmetry
Seemingly useless info, but I feel richer for knowing this.
Last edited by: gordonm888 on Mar 24, 2023
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
March 24th, 2023 at 9:12:31 PM
permalink
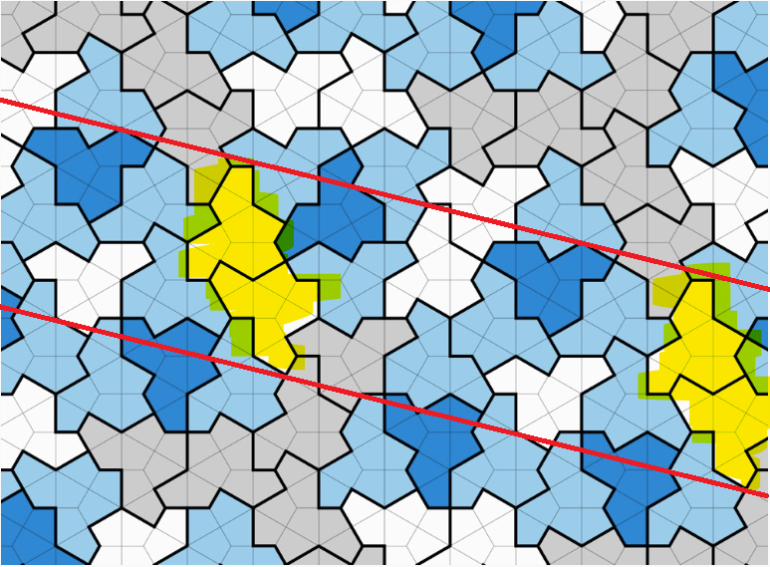
What am I not getting here? I see many tiles in repetition.
April 2nd, 2023 at 3:42:59 PM
permalink
Quote: rainmanWhat am I not getting here? I see many tiles in repetition.
link to original post
Completely agree.
April 3rd, 2023 at 5:18:31 AM
permalink
This YouTube video may help you to understand.Quote: rainmanWhat am I not getting here? I see many tiles in repetition.
link to original post
https://www.youtube.com/watch?v=-eqdj63nEr4&t=34s
Basically, yes, you can have patches that repeat... but if you slide the whole thing up and around, it will never completely line up with itself again.


