http://profootballtalk.nbcsports.com/2013/12/16/car-dealership-paying-out-420000-after-seahawks-shutout/
It cost an INSURANCE COMPANY that much.
It cost the car dealership only $7,000.
I believe that roughly 2% of NFL games involve a shutout in the first place, now throw in that the Giants have the NFC's worst performing offense, and second or third worst in the NFL combined with the Seattle defense now being the stingiest in the NFL and second or third going into the week.
I have to kind of scoff at the insurance company that they would make such a terrible lay. PMing the Wizard to see if he agrees with me. I think a fair lay would have been about 40:1.
Quote: Mission146It's a good thing they took out insurance, $7,000, it said. That's $7,000 not to pay $420,000, which is effectively a potential savings of $413,000. The insurance company basically laid 58:1 against a shutout, so I think the car dealership probably had the best of that one.
I believe that roughly 2% of NFL games involve a shutout in the first place, now throw in that the Giants have the NFC's worst performing offense, and second or third worst in the NFL combined with the Seattle defense now being the stingiest in the NFL and second or third going into the week.
I have to kind of scoff at the insurance company that they would make such a terrible lay. PMing the Wizard to see if he agrees with me. I think a fair lay would have been about 40:1.
Trust me when I tell you the Insurance Company wins on these "wagers" also. I was in the Insurance business for 13 years. Insurance Companies provide this type of insurance for all sorts of events. Hole in one golf events, half time half court shots, etc, etc. They always win in the long run, just as Casinos always win in the long run. Someone eventually wins and most of the time everyone loses.
ZCore13
| Estimated Points | Number in Sample | Total Zero Points | Ratio | 10 | 10 | 1 | 10.0% | 10.25 | 7 | 0 | 0.0% | 10.5 | 14 | 2 | 14.3% | 10.75 | 7 | 1 | 14.3% | 11 | 13 | 1 | 7.7% | 11.25 | 21 | 1 | 4.8% | 11.5 | 22 | 3 | 13.6% | 11.75 | 23 | 1 | 4.3% | 12 | 34 | 2 | 5.9% | 12.25 | 36 | 7 | 19.4% | 12.5 | 41 | 3 | 7.3% | 12.75 | 39 | 4 | 10.3% | 13 | 55 | 1 | 1.8% | 13.25 | 58 | 5 | 8.6% | 13.5 | 78 | 1 | 1.3% | 13.75 | 89 | 5 | 5.6% | 14 | 92 | 4 | 4.3% | 14.25 | 108 | 7 | 6.5% | 14.5 | 117 | 8 | 6.8% | 14.75 | 141 | 7 | 5.0% | 15 | 160 | 7 | 4.4% | 15.25 | 160 | 7 | 4.4% | 15.5 | 213 | 7 | 3.3% | 15.75 | 198 | 11 | 5.6% | 16 | 206 | 6 | 2.9% | 16.25 | 221 | 12 | 5.4% | 16.5 | 241 | 10 | 4.1% | 16.75 | 273 | 7 | 2.6% | 17 | 306 | 8 | 2.6% | 17.25 | 305 | 8 | 2.6% | 17.5 | 306 | 10 | 3.3% | 17.75 | 323 | 4 | 1.2% | 18 | 299 | 8 | 2.7% | 18.25 | 332 | 8 | 2.4% | 18.5 | 309 | 9 | 2.9% | 18.75 | 307 | 7 | 2.3% | 19 | 356 | 8 | 2.2% | 19.25 | 389 | 5 | 1.3% | 19.5 | 361 | 5 | 1.4% | 19.75 | 343 | 6 | 1.7% | 20 | 402 | 8 | 2.0% | 20.25 | 379 | 6 | 1.6% | 20.5 | 359 | 3 | 0.8% | 20.75 | 353 | 5 | 1.4% | 21 | 344 | 1 | 0.3% | 21.25 | 317 | 3 | 0.9% | 21.5 | 341 | 2 | 0.6% | 21.75 | 331 | 1 | 0.3% | 22 | 369 | 1 | 0.3% | 22.25 | 336 | 0 | 0.0% | 22.5 | 316 | 2 | 0.6% | 22.75 | 280 | 3 | 1.1% | 23 | 311 | 1 | 0.3% | 23.25 | 290 | 3 | 1.0% | 23.5 | 279 | 1 | 0.4% | 23.75 | 255 | 1 | 0.4% | 24 | 246 | 1 | 0.4% | 24.25 | 219 | 0 | 0.0% | 24.5 | 230 | 2 | 0.9% | 24.75 | 230 | 1 | 0.4% | 25 | 212 | 2 | 0.9% | 25.25 | 207 | 0 | 0.0% | 25.5 | 176 | 1 | 0.6% | 25.75 | 154 | 0 | 0.0% | 26 | 154 | 1 | 0.6% | 26.25 | 113 | 0 | 0.0% | 26.5 | 137 | 0 | 0.0% | 26.75 | 122 | 0 | 0.0% | 27 | 95 | 0 | 0.0% | 27.25 | 98 | 0 | 0.0% | 27.5 | 83 | 0 | 0.0% | 27.75 | 81 | 0 | 0.0% | 28 | 82 | 0 | 0.0% | 28.25 | 55 | 1 | 1.8% | 28.5 | 56 | 0 | 0.0% | 28.75 | 51 | 0 | 0.0% | 29 | 48 | 0 | 0.0% | 29.25 | 34 | 0 | 0.0% | 29.5 | 24 | 0 | 0.0% | 29.75 | 25 | 0 | 0.0% | 30 | 24 | 0 | 0.0% |
|---|
Overall, a team will score zero points 1.79% of the time.
Using logistic regression, I find:
Probability zero points = exp(x)/(1+exp(x)),
where:
x = 1.562545 + -0.302485 * y
y = estimated points
As mentioned in my last post, the total in that game was 41, and the Seahawks were a 7-point favorite. Doing a little algebra we see the estimated points by the Giants is 17 and Seahawks is 24.
So, in this case y=17 and x = -3.579706.
The probability the Giants score zero points is thus exp(-3.579706)/(1+exp(-3.579706)) = 2.71%.
Given that the policy had a face value of 12 * $35,000 = $420,000, the fair cost should have been 2.71% * $420,000 = $11,384.
Thus, the dealership got a great bargain paying only $7,000! Normally, insurance companies that insure oddball stuff like this charge double the expected cost. In this case, I would have charged $22,768 for that policy.
If I were the mathematician that calculated that premium I'd be pretty nervous this morning, hoping the boss doesn't review the math, which he probably will considering he will have to write a check for $420,000.
Quote: WizardThe following table shows how often a team scored zero point according to the estimated number of points it would score, based on the point spread and total. Data is based on the 1983 to 2012 seasons, inclusive.
Estimated Points Number in Sample Total Zero Points Ratio 10 10 1 10.0% 10.25 7 0 0.0% 10.5 14 2 14.3% 10.75 7 1 14.3% 11 13 1 7.7% 11.25 21 1 4.8% 11.5 22 3 13.6% 11.75 23 1 4.3% 12 34 2 5.9% 12.25 36 7 19.4% 12.5 41 3 7.3% 12.75 39 4 10.3% 13 55 1 1.8% 13.25 58 5 8.6% 13.5 78 1 1.3% 13.75 89 5 5.6% 14 92 4 4.3% 14.25 108 7 6.5% 14.5 117 8 6.8% 14.75 141 7 5.0% 15 160 7 4.4% 15.25 160 7 4.4% 15.5 213 7 3.3% 15.75 198 11 5.6% 16 206 6 2.9% 16.25 221 12 5.4% 16.5 241 10 4.1% 16.75 273 7 2.6% 17 306 8 2.6% 17.25 305 8 2.6% 17.5 306 10 3.3% 17.75 323 4 1.2% 18 299 8 2.7% 18.25 332 8 2.4% 18.5 309 9 2.9% 18.75 307 7 2.3% 19 356 8 2.2% 19.25 389 5 1.3% 19.5 361 5 1.4% 19.75 343 6 1.7% 20 402 8 2.0% 20.25 379 6 1.6% 20.5 359 3 0.8% 20.75 353 5 1.4% 21 344 1 0.3% 21.25 317 3 0.9% 21.5 341 2 0.6% 21.75 331 1 0.3% 22 369 1 0.3% 22.25 336 0 0.0% 22.5 316 2 0.6% 22.75 280 3 1.1% 23 311 1 0.3% 23.25 290 3 1.0% 23.5 279 1 0.4% 23.75 255 1 0.4% 24 246 1 0.4% 24.25 219 0 0.0% 24.5 230 2 0.9% 24.75 230 1 0.4% 25 212 2 0.9% 25.25 207 0 0.0% 25.5 176 1 0.6% 25.75 154 0 0.0% 26 154 1 0.6% 26.25 113 0 0.0% 26.5 137 0 0.0% 26.75 122 0 0.0% 27 95 0 0.0% 27.25 98 0 0.0% 27.5 83 0 0.0% 27.75 81 0 0.0% 28 82 0 0.0% 28.25 55 1 1.8% 28.5 56 0 0.0% 28.75 51 0 0.0% 29 48 0 0.0% 29.25 34 0 0.0% 29.5 24 0 0.0% 29.75 25 0 0.0% 30 24 0 0.0%
Overall, a team will score zero points 1.79% of the time.
Using logistic regression, I find:
Probability zero points = exp(x)/(1+exp(x)),
where:
x = 1.562545 + -0.302485 * y
y = estimated points
As mentioned in my last post, the total in that game was 41, and the Seahawks were a 7-point favorite. Doing a little algebra we see the estimated points by the Giants is 17 and Seahawks is 24.
So, in this case y=17 and x = -3.579706.
The probability the Giants score zero points is thus exp(-3.579706)/(1+exp(-3.579706)) = 2.71%.
Given that the policy had a face value of 12 * $35,000 = $420,000, the fair cost should have been 2.71% * $420,000 = $11,384.
Thus, the dealership got a great bargain paying only $7,000! Normally, insurance companies that insure oddball stuff like this charge double the expected cost. In this case, I would have charged $22,768 for that policy.
If I were the mathematician that calculated that premium I'd be pretty nervous this morning, hoping the boss doesn't review the math, which he probably will considering he will have to write a check for $420,000.
Hope the BOSS does not see this!!!!!!!!!!!
Quote: DJTeddyBearNope.
It cost an INSURANCE COMPANY that much.
It cost the car dealership only $7,000.
Nope.... Insurance companies lay off their action in the re-insurance market. So one insurance company gets the publicity and is primary payor but other companies have to contribute.
Quote: FleaStiffNope.... Insurance companies lay off their action in the re-insurance market. So one insurance company gets the publicity and is primary payor but other companies have to contribute.
This is getting out of my area, but I think insurance companies only lay off risk they are too small to assume. For example, a small insurance company might not be comfortable writing a 20-million dollar life insurance policy, so they re-insure it with a bigger insurance company. Anybody in the insurance business should be able to fork over $420,000 on their own. Not to mention that I doubt re-insurance companies dabble in promotional risks like this.
Quote:Hope the BOSS does not see this!!!!!!!!!!!
If he does, I hope he'll keep me in mind if my income continues to decline, and I need to find a real job.

Quote: WizardThis is getting out of my area, but I think insurance companies only lay off risk they are too small to assume. For example, a small insurance company might not be comfortable writing a 20-million dollar life insurance policy, so they re-insure it with a bigger insurance company. Anybody in the insurance business should be able to fork over $420,000 on their own. Not to mention that I doubt re-insurance companies dabble in promotional risks like this.
If he does, I hope he'll keep me in mind if my income continues to decline, and I need to find a real job.
Yeah, most of these companies that do "event policies" don't lay off any of the risk. The risked amount (and risk itself) is not high enough.
In this case, they probably have a "shutout" event policy for NFL football that doesn't deviate from game to game. The event has to be planned out a long time ahead of time. Sometimes a year in advance. My guess is the Wizard's evaluation of the risk is way more than the company used to determine the premium because they would have had no idea how good or bad the Giants would be at this point in the year.
ZCore13
Quote: AlanJust for the heck of it I Googled "Hole In One" insurance, to kind of get an idea of cost. I didn't research it, just grabbed a random link. Here are some rates:
Very interesting. I appreciate how the premium difference between the $3k Hawaii vacation and $15k Motorcycle is 2x/4x (for 5x more of a prize) whereas the difference between a $30k Challenger and $60k Mercedes is <2x (for a 2x more of a prize). I'd be very interested to know how much they expect to earn on each. For the 72 player one, it probably isn't even worth their time to take less than $150.
Quote: ahiromuQuote: AlanJust for the heck of it I Googled "Hole In One" insurance, to kind of get an idea of cost. I didn't research it, just grabbed a random link. Here are some rates:
Very interesting. I appreciate how the premium difference between the $3k Hawaii vacation and $15k Motorcycle is 2x/4x (for 5x more of a prize) whereas the difference between a $30k Challenger and $60k Mercedes is <2x (for a 2x more of a prize). I'd be very interested to know how much they expect to earn on each. For the 72 player one, it probably isn't even worth their time to take less than $150.
$150 is their minimum premium. If someone asked for a $1,000 prize with 20 players it would still be $150.
ZCore13
Not so. Insurance commissioners like to see just about everything re-insured except the really small potatoes and really short term stuff that is not amenable to re-insurance markets. That is the way small insurance companies can keep underwriting new policies and small bail bond companies can write bond on many defendants all subject to the same real estate parcel.Quote: WizardThis is getting out of my area, but I think insurance companies only lay off risk they are too small to assume.
> Not to mention that I doubt re-insurance companies dabble in promotional risks like this.
You think Betty Grable's legs were insured because that company was an expert in movie stars legs? The policy risks were laid off because no insurance company is an expert in movie stars legs. Its often the same way with contests and lottery sales of real estate by a charity. Its small potatoes and takes time, but once the policy is written, it goes out for re-insurance.
>If he does, I hope he'll keep me in mind if my income continues to decline, and I need to find a real job.
LOL. Just follow the advice you read here about Mr. Martingale and his "Double Up to Catch Up" phrase. It didn't make his customers rich but it sure made him rich. And for every Anzac Day, fly the family to Australia and go Tails All the Way at Three-Up.
Quote: FleaStiffNot so. Insurance commissioners like to see just about everything re-insured except the really small potatoes and really short term stuff that is not amenable to re-insurance markets. That is the way small insurance companies can keep underwriting new policies and small bail bond companies can write bond on many defendants all subject to the same real estate parcel.
> Not to mention that I doubt re-insurance companies dabble in promotional risks like this.
You think Betty Grable's legs were insured because that company was an expert in movie stars legs? The policy risks were laid off because no insurance company is an expert in movie stars legs. Its often the same way with contests and lottery sales of real estate by a charity. Its small potatoes and takes time, but once the policy is written, it goes out for re-insurance.
>If he does, I hope he'll keep me in mind if my income continues to decline, and I need to find a real job.
LOL. Just follow the advice you read here about Mr. Martingale and his "Double Up to Catch Up" phrase. It didn't make his customers rich but it sure made him rich. And for every Anzac Day, fly the family to Australia and go Tails All the Way at Three-Up.
Where are you getting your info Flea? 99% of Insurance Companies don't offer event insurance. As a matter of fact, the biggest player in the market, Lloyd's of London isn't even an Insurance Company. It's a group of VERY wealthy individuals. They specialize in providing re-insurance and high value event insurance.
I don't know for sure, but I'd put a lot of money that Lloyd's is the Company that would have insured Betty Grable's legs. They insure Troy Polamalu's hair for $1,000,000 among other athletes and celebrity body parts. The companies that do specialize in event coverage do not generally lay off the risk.
ZCore13
Quote: FleaStiffNot so. Insurance commissioners like to see just about everything re-insured except the really small potatoes and really short term stuff that is not amenable to re-insurance markets.
How do you know?
Getting back on topic, here is a chart showing the probability of a shutout, both actual percentage and estimated.
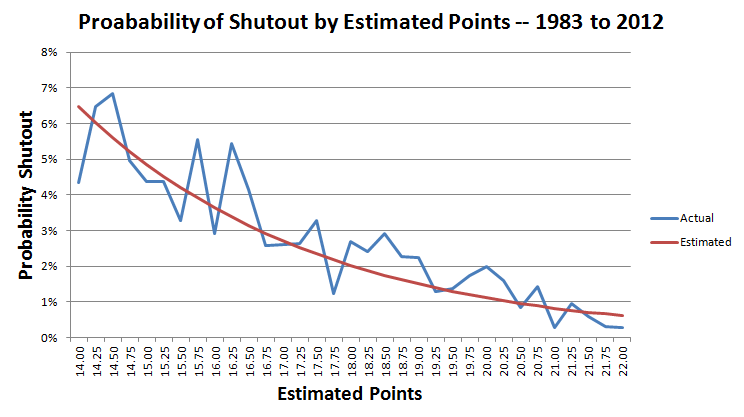
In the UK bookies take bets like this. Recently someone won £125k when his £50 bet came in after his grandson played for Wales. see http://www.dailymail.co.uk/sport/football/article-2463232/Harry-Wilson-grandad-wins-125-000-bet-Liverpool-kids-Wales-debut.htmlQuote: Zcore13...companies that do specialize in event coverage do not generally lay off the risk...
Quote: Zcore13
In this case, they probably have a "shutout" event policy for NFL football that doesn't deviate from game to game. The event has to be planned out a long time ahead of time. Sometimes a year in advance. My guess is the Wizard's evaluation of the risk is way more than the company used to determine the premium because they would have had no idea how good or bad the Giants would be at this point in the year.
I should imagine that is generally the case, but the article:
http://profootballtalk.nbcsports.com/2013/12/16/car-dealership-paying-out-420000-after-seahawks-shutout/
States in part:
Quote:Johnson also said that they wanted to run the promotion the previous week, when the Seahawks lost 19-17 to the 49ers, but couldn’t get the logistics squared away in time.
Thus, I'd be inclined to believe it was a fairly short-term decision and very bad work by the insurance analyst.
I've also been gloating because my implied fair odds laying 40:1, with an implied 2.5% probability, were very close to Wizard's figures. Wizard said (correctly) that $11,384 was fair, and I'd be at $10,500.
Either way, that guy might be fired, they should hire Wizard...and if I worked there, I'd probably get a stern warning but still keep my job!
Obviously, the Seahawks policy was much too cheap for the odds.
Quote: sodawater
Obviously, the Seahawks policy was much too cheap for the odds.
The article said they tried to do it the week before so I wonder if the price was derived based on the 49'ers game, but then applied to the Giants game.
Quote: FleaStiffNot so. Insurance commissioners like to see just about everything re-insured except the really small potatoes and really short term stuff that is not amenable to re-insurance markets.
I'll ask a second time -- how do you know?


