Video Poker Bankroll

I'm new to this site, but I hope you guys can help me! I've been trying to find, or adapt some sort of equation to figure out video poker bankroll requirements. I did not see anything listed about this anywhere on the forum.

What I'd like to know is, with any given game and it's variance, is it possible to say, with a given confidence level, that a bankroll will last over a set number of hands in a session?

Specifically, if I am playing $1 9/6 JoB, and I want to play a 4-hour session, which we will call 2,000 hands, how much do I need to say with 90% confidence that I will not run out of money before the 2,000 hands is over? I assume the variance and return need to be plugged in somewhere, I just can't seem to figure out where in a way that makes sense... Thanks!!

The Wizard has a basic RoR VP page here.
It may not be what you want
Video Poker: Bankroll size vs. Risk of Ruin

Alan Krigman has a formula here
A New Formula for Video Poker
"I've developed a formula linking bankroll, bet size, spins per session, confidence you'll remain in action, and house advantage. Starting with any four of these variables, you can find the other -- provided you can use a calculator, spreadsheet, or paper and pencil to do addition, subtraction, multiplication, and division."

Hope it helps out

added:
my values (edit)
0.90 $1062 (10% RoR)
0.95 $1203 (5% RoR)
0.99 $1346 (1% RoR)

Krigman's values
0.90 $1160 (10% RoR)
0.95 $1335 (5% RoR)
0.99 $1519 (1% RoR)

Thanks, Guido!!

This does help!! I had seen the Wizard's RoR page, but you are correct, though helpful, was not exactly what I was looking for in this case.

The question that I still have...

Using Alan Krigman's formula, the numbers seem like they would be pretty close. For the fun of it, I compared JoB with DDB using the formula, and the bankroll requirements were surprisingly close. Since the variance on these games is quite different, would this necessarily have an affect on the result? Or is the variance simply a result of the overall EV?

He also had some "default" numbers plugged into his formula, but I did not see in his article where he came up with those figures...

Approximately $875, according to this:

Quote: jimthecat

Using Alan Krigman's formula, the numbers seem like they would be pretty close.
For the fun of it, I compared JoB with DDB using the formula, and the bankroll requirements were surprisingly close.
Since the variance on these games is quite different, would this necessarily have an affect on the result? Or is the variance simply a result of the overall EV?

He also had some "default" numbers plugged into his formula, but I did not see in his article where he came up with those figures...

B = [(R) x (W)]/[29.3 + (53.1 x E) - (22.7 x S)]
from the above photo, looks like sim results in a program
sim data is always good if it is accurate in the code and has a large enough sample size

Looks like the 22.7 could be the WagerSD
53.1 may be the nothing probability*100
29.3 ??
I need some time to see what others have and maybe just email Krigman and ask him.
He seems to use this formula, from 2000, a lot even in his later articles along with his simulation results.

A trip or session bankroll RoR seems to be a commonly asked question with really no common answers.
Most responses to Bankroll and RoR are like this... kind of blue-skyish
"A safe bankroll for Full Pay Jacks or Better might be about three times a royal (4,000 credits times three or 12,000 credits). A safe bankroll for a Full Pay Double Bonus Poker game might be about 3.5 to 4 times a royal or 14,000 to 16,000 credits -- not a small difference"

This is where simulations can really help out

FWIW,
I just take $1000 when I want to put in $10k in a $ 9/6 JoB...

Ruleof the thumb:

25 cents JOB 9/6 bankroll $1, 000.-- amount of Royal Flush

$ 1 JOB bankroll 9/6 $ 4, 000.-- amount of Royal Flush

removed
silly

Quote: mustangsally

These rules of thumbs give what kind of a Risk of Ruin?
Normal distribution will be too high for a bankroll requirement as it does not consider the high positive skew.
ev: -45.61
1sd: 988
2SD (a $2K bankroll is too high by my simulations and the one posted above) should be about a 10% RoR

Looks like sim data or a proper RoR formula is the best path to take to know one's chances of lasting a certain session length.

Correct.
LIFETIME BANKROLL for any denom JoB would be like 3x a royal. ($3000, $12000)
However, if you can replinish your bankroll between sessions, then you only need to bring a certain amount for each session (such as me, I'll play one session a month, and bring $1000 for each session...although it EQUALS $12000 over the course of the year)

Quote: TIMSPEED

Correct.
LIFETIME BANKROLL for any denom JoB would be like 3x a royal. ($3000, $12000)

Like that seems to be a very generalized statement and does not agree at all with the Wizard's calculations that consider Risk of Ruin.

The OP asked a specific trip/session Bankroll/RoR question and these rules of thumbs really do not answer his or these type of questions.
The VP for Winners software looks to be a good place to start with Krigman's formula.

Quote: QuadDeuces

Approximately $875, according to this:

Nice find QD!
"The bankroll calculator computes and displays the probability distribution for a player's bankroll after an arbitrary number of hands of a selected game. "
This could also be done fast in Excel with some VB code or slow just making tables.

Just playing with a few tables, this Bankroll Calculator looks to be quite accurate.
It does not use simulation for the results.
$875 being 175 betting units

Very nice!

Quote: jimthecat

For the fun of it, I compared JoB with DDB using the formula, and the bankroll requirements were surprisingly close. Since the variance on these games is quite different, would this necessarily have an affect on the result? Or is the variance simply a result of the overall EV?

He also had some "default" numbers plugged into his formula, but I did not see in his article where he came up with those figures...

The 10/6 DDB from VP for Winners shows a Bankroll of $1630 for a 10% RoR.



Krigman's formula may need some major adjusting from what it currently shows.
The formula values could also just have some errors in them. Who knows.

VP for Winners is a nice software find.
Sally

removed
silly
Sally

Quote: jimthecat

Specifically, if I am playing $1 9/6 JoB, and I want to play a 4-hour session, which we will call 2,000 hands,
how much do I need to say with 90% confidence that I will not run out of money before the 2,000 hands is over?
I assume the variance and return need to be plugged in somewhere, I just can't seem to figure out where in a way that makes sense... Thanks!!

It now appears that there is no session bankroll/RoR formula that is very accurate available due to not only the variance but one that would also consider the skewness.

The VP for Winners soft and Dunbar's Risk Analyzer for video poker (Excel based VBA) are 2 good options.
I know some VBA so I may go with Dunbar's program, it is cheaper cost by $30 and one can do a lot of stuff in Excel.

The VP for Winners soft, to me, is very slow calculating the probability distribution.

The Gambler's Odds software (free download)
http://www.gamblecraft.com/soft/odds/index.htm
is way faster than VPW. I like it.
But they all get to the final answers.

Looks like this thread ended up looking at a few programs to use.

Final results for OP
$1245 bankroll
1.07% RoR
31.22% prob of a net win
68.42% prob of a net loss
4.32% +$2000 net win

$1010 bankroll
4.98% RoR
31.18% prob of a net win
68.46% prob of a net loss
4.79% +$2000 net win

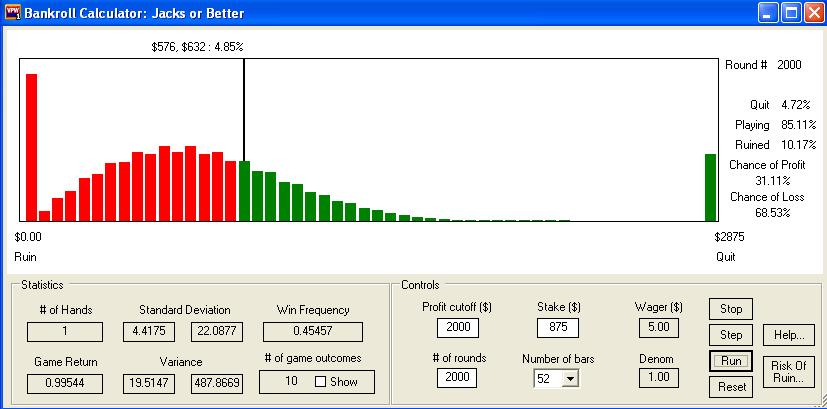
$875 bankroll
10.17% RoR
31.11% prob of a net win
68.53% prob of a net loss
4.72% +$2000 net win

A 10% RoR means that 1 in 10 (10 out of 100 etc) sessions of length 2000, on average, will end in complete ruin.

Enjoy!

Wow! Thanks everybody! Especially Sally, Guido, and Deuces!

These numbers are in line with what I have come up with using these formulas.

Until recently, I'd just go to the casino and put a couple bills into a machine, and, although I basically knew the strategy, it rarely ended in anything but ruin, which of course is partially due to the size of the bankroll I was using.

I like to look at it using this approach (bankroll per session), as I do have the ability to put a little bit toward playing each week from my regular income. I've become a little obsessive with trying to find the best machines, using the Wizard's information on his site and also the links that he provides.

Thanks again to all of you for the help!

Quote: guido111

$1010 bankroll
4.98% RoR
31.18% prob of a net win
68.46% prob of a net loss
4.79% +$2000 net win
2,000 hands played
JoB 9/6

You are welcome.
This was a bit fun seeing what is all available to us.
A bit disappointed in Krigman's formula results, but at least it was a start.

One can also see from the 5% RoR numbers, that you have about the same chance of ruin as you do to win $2000.
That is the good side of variance.

Here is a graph of 3000 hands with the $1010 bankroll.
You can see it (Risk of Ruin) rises quite quickly.
The 5% is at 2k hands but is 10% by the ~2,500th hand and is over 15% by the 3,000th hand.


It just shows the longer you play, or the more sessions one plays, the higher the bust rate becomes and the more luck, more paying higher hands are needed to show a profit.

Those 30%+ chances of coming out ahead shows most sessions end a loser.
Most VP players refuse to accept this fact.

Good Luck and thanks for your question.