I would assume so but interested to hear from someone wiser than me.
Standard Deviation squared IS Variance.
If what you're asking is how to calculate STD DEV over multiple trials it's pretty easy. The formula is (SQRT of # of trials) * STD DEV. So if it was 100 trials with a STD DEV of 5, then the result would be a STD DEV of 50.
Quote: Walkinshaw30tJust wondering about the variance of standard deviation, does standard deviation of a certain number of events have the same standard deviation applied to it ?
usually there is a suggestion you read up on it.
First step might be the terms, you are using two of them in your question. You seem to have a grip on variance. The standard deviation is the square root of the variance. I guess it must be true that the variance of standard deviations has a standard deviation, that brings a smile. Once we get this standard deviation of whatever, we get meaning out of a range of numbers.
Clearly the number of events, say the number of bets, does not always produce the same SD. You must be aware that various games have different variances associated with them. Thus the SDs must be different.
I am no math whiz so I can relate to someone trying to comprehend this. The problem for us is that the concept is fairly simple, but the math is not. Here are the hieroglyphics they throw at you.
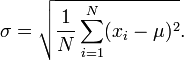
There are calculators as below. This one shows the mean; in Craps you know that should be 7.
I inserted this range of results:
2,3,3,4,4,4,5,5,5,5,6,6,6,6,6,7,7,7,7,7,7,8,8,8,8,8,9,9,9,9,10,10,10,11,11,12
which Craps players know is a perfect distribution of 36 throws. The mean was indeed calculated to be 7. edit:the SD of Craps is supposed to be close to 1, but I think this is different because there is a range of 36.
For gamblers, for the most part you try to understand the concept, but you rely on the mathematicians to arrive at the facts.
http://www.calculator.net/standard-deviation-calculator.html
The intent of the question is to find out if an outcome that is more than 2 standard deviations away from expected result in a certain number of events happens less than 5% of the time, in a group of 100 trials of that same number of events can I rely on the probability that 5 of those times will be over 2 standard deviations from a average or because of low occurance of being more than 2 standard deviations is there a high variance to the number of times that the results will be more than 2 standard deviations.
Eg betting on a single number in roulette has a low probability of hitting and therefore has a much higher variance than an even chance bet.
I hope I make some kinda sense!
Cheers
I have no math to show you on that.
Quote: odiousgambitI guess it must be true that the variance of standard deviations has a standard deviation
The is a conceptual misunderstanding here.
Standard deviation (or it's square the variance) is a property of the statistical ensemble itself. For example in roulette for a given bet, the ensemble consists of all possible spin result with their subsequent payoffs. In Baccarat it consists of all possible combinations of the next 6 cards in the shoe.
If you know the whole ensemble, you can *calculate* the standard deviation. This is a simple task in roulette (there are only 37 or 38 possible outcomes), but is more difficult in card games.
So the standard deviation is as fixed as the rules of the game. The standard deviation of the standard deviation is exactly *zero*, as for any other constant.
Now let's look at a different scenario: Imagine some new game is served, but you don't know the rules of the game at all. You still want to know it's standard deviation. Other than asking the provider or their inventors - since you can't calculate the standard deviation from the ensemble (as you don't know any rules), you will never know the standard deviation. So how do you handle this problem ? You can still place bets and observe the outcomes of the bets. Do it multiple times. From your results you can get *estimates* of the standard deviation by some clever formulas. But these estimates are very different from the (ensemble) standard deviation, as the estimates *do* fluctuate (every different series of results gives you a different estimate).
Back to the original question: There is a non-zero standard deviation of estimates of standard deviations. These depends of course depend on the ensemble standard deviation, but also on the estimator details - mainly the number of tries.
Quote: MangoJThere is a non-zero standard deviation of estimates of standard deviations.
Yes, but look closely at what he is asking. It seems that once you know the S.D. of what you are playing, it is only natural to wonder how much you can depend on it. Let's say the 2.5% chance of the worst outcomes [say being outside 3 S.D.s on the wrong end] would be important to the player; he decides he can survive that occurring, but not having 5% land there. How much can he count on it?
I must quickly bow to superior knowledge but it seems to me the question is valid. Would it be true that anything that deviates should have a standard deviation? Otherwise aren't you saying he can absolutely count on his luck not being worse than that bell-shaped curve indicates?
Quote: odiousgambitYes, but look closely at what he is asking. It seems that once you know the S.D. of what you are playing, it is only natural to wonder how much you can depend on it. Let's say the 2.5% chance of the worst outcomes [say being outside 3 S.D.s on the wrong end] would be important to the player; he decides he can survive that occurring, but not having 5% land there. How much can he count on it?
I must quickly bow to superior knowledge but it seems to me the question is valid. Would it be true that anything that deviates should have a standard deviation? Otherwise aren't you saying he can absolutely count on his luck not being worse than that bell-shaped curve indicates?
If anyone can give some input on this it would be much appreciated...
Your question "does standard deviation of a certain number of events have the same standard deviation applied to it ?" doesn't make much sense.
The standard deviation of an event is a fixed quantity (at least in the frequentist statistics view), so is the standard deviation of any number of events.
Hence the standard deviation of the "standard deviation of a certain number of events" is zero, no ?
My gut reaction mathy answer:
Your goal is to estimate the sd. Hence you want to know how to estimate variance of the sd so you can construct a confidence interval around your sd estimate. Is that right?
Quote: endermikeI have perused the thread but am still unclear on the question you wish answered. Before I try to give you a "mathy" explanation can you please try to give me a concrete, real-world example?
My gut reaction mathy answer:
Your goal is to estimate the sd. Hence you want to know how to estimate variance of the sd so you can construct a confidence interval around your sd estimate. Is that right?
Yes that is correct.
http://graphpad.com/support/faqid/1381/
http://www.stat.purdue.edu/~tlzhang/stat511/chapter7_4.pdf
http://en.wikipedia.org/wiki/Variance#Distribution_of_the_sample_variance
http://en.wikipedia.org/wiki/Standard_deviation#Confidence_interval_of_a_sampled_standard_deviation
If they don't clear things up post again.
elderly the most. Just say no to standard
deviation.
Quote: Walkinshaw30tJust wondering about the variance of standard deviation, does standard deviation of a certain number of events have the same standard deviation applied to it ?
I would assume so but interested to hear from someone wiser than me.
I don't know about "wiser" but I'll add, in good faith, what I can.
For any random population of outcomes (from dice to shoe sizes) the Central Limit Theorem predicts a convergence of the Probability Density Function (PDF) to be the familiar Gaussian Normal (bell) curve. This assumes that the individual outcomes are not correlated (e.g. I don't just use 100 measurements of my own shoe size, but select them randomly from a diverse set of unrelated strangers). The Normal distribution, if it applies to your problem is attractive for the following reasons:
I think you probably already knew this, but I mentioned any as background. Now the water gets deeper.
OK, I'm getting off topic. Sorry. Let me paraphrase what I think you're asking, and you tell me how close I am to your question. Yes there is such a thing as a standard deviation of a standard deviation, but not for the simple bell curves of the type which best apply for you. IOW, if we consider the standard deviation to be the "first moment" of a distribution, there are also "second moments" and "third moments" and so on. But these "higher moments" are only non-zero for more complex curves than the bell curve. [The fourth standardized moment is sometimes called the kurtosis.] There are also a whole family of "skewed" curves which represent certain populations better than the bell curve.
To summarize, the worst question you can ask of probability theory is "is it possible" because the answer is almost always yes, but usually too loose to have any practical value for making "real life" decisions. Example: Is it possible that all the air molecules in my room will accidentally end up in one corner (just by chance) and I'll suffocate? Yes, it is possible (people have even computed the remote odds of this happening)! But seriously, is that any reason for most of us to care?
Instead, ask how probable something is because therein lies the path to practical wisdom (making the best bet, or finding the "optimal" course of action in daily life. Hope this helps.
Yes that answers what I wanted and gives me a further understanding overall.
I appreciate you taking the time to explain it to me.
Cheers mate
A random variable (your win/loss on one bet with stake 1) has a mean of M and a standard deviation S. If it were Normal-Gaussian, it would mean that the probability of getting a value higher than two S above M (M+2S) is equal to 2.28%. But one bet is not Gaussian distributed.
If you bet a stake of 100, then your mean is 100M and your SD is 100S. Same conclusions about the probabilities. Still not Gaussian.
Now if you repeatedly bet 1, a hundred independent times, then your overall win/loss has a mean of 100M but a standard deviation of only 10S. Also, the repetition kicks in the theorem that says it finally resembles a Gaussian distribution. Hence you CAN say that the probability of reaching 100M+20S is 2.28%
Example: roulette, red/black.
M = -2/38 = -0.0526 s = 0.2233
100 trials:
100m = -5.263 ; 20s = 4.466
There is but 2.28% chance that your final result is above -0.797
(and only 0.95% of not being negative).
I think you used "variance" as simply meaning "change" in the original post. Beware! it has a very specific meaning in probability theory.
said 'Victim of Standard Deviation'. It's insidious.
Standard Deviation = Sqrt(# trials) x Standard Deviation !!!
This works out to Standard Deviation/Standard Deviation = Sqrt(# trials), OR Sqrt(#trials) = 1 !!!!!
No, but if you could find a way to circumvent the 2nd Law, you'd be a billionaire.Quote: JohnBIs it true that the 2nd law of Thermodynamics can be used for profit in casino games like roulette?
link to original post
Quote: JohnBSeriously: the constant movement between disequilibria promises opportunities. Since it is known in which direction the movement is, it should be possible to take advantage of this knowledge. Is it a matter of stack or tablelimits?
link to original post
Taking advantage of movement between disequilibria would seem to require dependent trials.


