Probability

Hello Wizzard/members,

I am looking for the probability of the following event on a single zero roulette wheel.

You select 5 numbers, say: 1,2,3,4,5

What is the probability of all 5 numbers coming up in 10 spins?

I really need to know the answer to this and the maths behind it.

Start with calculating the probability of either hitting 0 or 1 of your numbers on the first game.



If you hit 1 of them, then you have 4 left to collect. So, what is the probability that you will collect a 2nd number on the second spin (or 0 total or 1 total)? Essentially, build off of your previous answers.

First Spin: 5/37
Second Spin: 4/37
Third Spin: 3/37
Fourth Spin: 2/37
Fifth Spin: 1/37

Multiply the probabilities together, you have a chance of all 5 of them hitting in 5 spins of: .0000017, or .00017%

Note: this doesn't include repeat numbers winning... So if 1 came up twice in a row, that doesn't win. I'm doing that you literally hit each of the numbers 1-5 in 5 spins.

Here's how I would do it:

Let S(a,b) be a state value where a = the number of spins up to that point (from 0 to 10), and b = (10000 if 1 has been spun at least once) + (1000 if 2 has been spun at least once) + (100 if 3 has been spun at least once) + (10 if 4 has been spun at least once) + (1 if 5 has been spun at least once). b is expressed with leading zeroes to make it easier to understand; e.g. if 3 and 5 have been spun in the first 6 spins but 1, 2, and 4 have not, then this is S(6, 00101).

S(0, 00000) = 1; S(0, N) = 0 for N > 0.
For each N > 0, there are six ways to reach state S(N, abcde):
(1) If a = 1, S(N-1, 0bcde) x 1/37
(2) If b = 1, S(N-1, a0cde) x 1/37
(3) If c = 1, S(N-1, ab0de) x 1/37
(4) If d = 1, S(N-1, abc0e) x 1/37
(5) If e = 1, S(N-1, abcd0) x 1/37
(6) S(N-1, abcde) x (1 - (the number of 0s in abcde / 37)).
#6 comes from the fact that there are two ways that abcde does not change; either you spin one of the 32 numbers other than 1 through 5, or you spin a number that has already been spun.
Work your way from the S(0, N) values to S(10, 11111).
I get somewhere around 1 / 3242, which comes close to what I get through simulation.

One way is to work out the various possible outcomes that result in your desired result and add them up. If we assume "x" means any of the other numbers, then the winners include:-
No Pairs: 12345xxxxx (in any order)
One Pair: 123455xxxx, 123445xxxx, etc.
Two Pairs: 1234455xxx, etc.
Three Pairs... etc.

Another method is to use a state method. For instance S(m,n) means having found m numbers in n spins. S(1,1) = 5/37 [UK] S(0,1)=32/37. S(1,2) = 33/37*S(1,1)+5/37*S(0,1).... Continue until you get S(5,10).

As they say, I'll leave the rest to the reader.

Quote: ThatDonGuy

...
I get somewhere around 1 / 3242, which comes close to what I get through simulation.

I get that answer ( 1 / 3242.06399 ), too, but with charliepatrick's first method. I found the probability of each of the nineteen patterns (no pairs, 1 pair, 1 pair with three-of-a-kind, 2 pairs, 3 pairs, 4 pairs, 5 pairs, etc.) and added them up.

Quote: ChrisSA

I really need to know the answer to this and the maths behind it.

really need to know?
really!

OK

I love Markov chains

a spreadsheet really helps out with simple multiply and adding numbers (I use Excel 2007 for this)

here is the transition matrix (the first section with fractions)

it basically shows the probs of moving from one state to another (where the states are the number of your numbers hit from 0 to 5)
an answer also shows in the row 0 column 5 (after raising the matix to the 10th power)


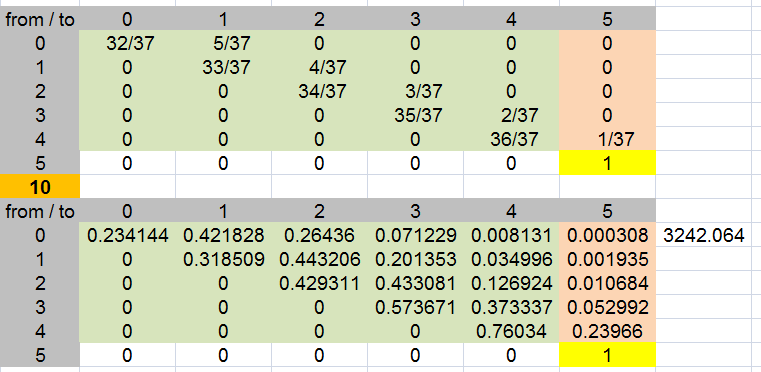
note: the row probs add up to 1 in the fraction section

many find it easy to see how one can move between the 6 states
but the math is a bit challenging multiplying matrices for many (computers do help out)

=========================================================
so another method using the transition probabilities that is very simple, in me opinion,
even my 11 year old nephew can do it, is a recursive method using the transition probs already shown



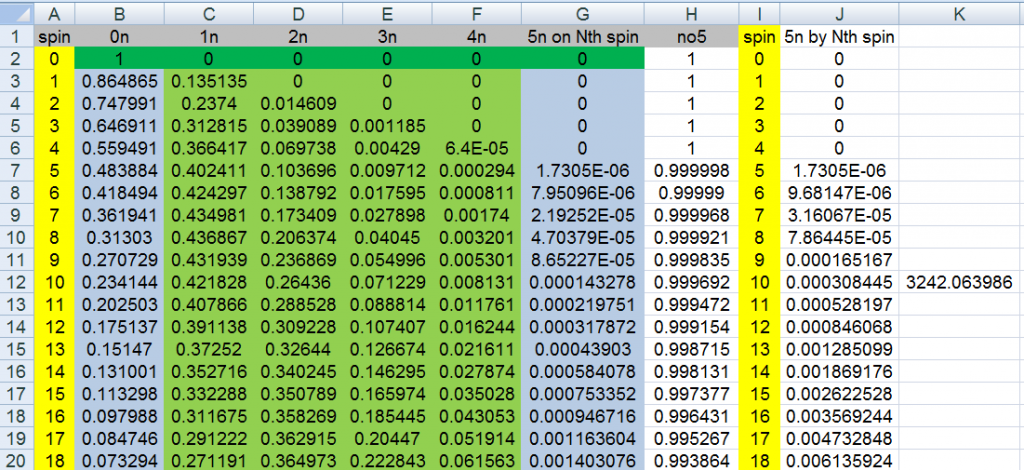
the row spin0 (row 2) is the probs of being there at spin #0
well, that should be easy as we have yet to spin one time.

now row spin1 (row 3)
colB: =(32/37)*B2
colC: =(5/37)*B2 + (33/37)*C2
colD: =(4/37)*C2 + (34/37)*D2
colE: =(3/37)*D2 + (35/37)*E2
colF: =(2/37)*E2 + (36/37)*F2
colG: =1/37*F2

fill down the row to as far as you want
I went to 200

here is the median
75: 0.497667449
76: 0.507936154


we can also see after each spin the probabilities of being in one of the 6 states

after 10 spins you are most likely to only have hit one of your numbers (and that could be at least 1 time)
also, by adding, I see a 0.920331611 probability of having either 0,1 or 2 of your numbers hit after the 10th spin


ask away if you really need to

remember you can get to a state by hitting a new number of yours or by staying at where you are
it is random

Sally

added: I would try 3 numbers at less than 1 in 94 (93.6007)
but tell why you really need to know?
Don says "please"

Hello everyone, thank you for your help, much appreciated.

A friend of mine asked me to get this answer as he wants to incorporate this bet into a slot machine somehow.

I will forward the maths to him.

Thanks once again.

Chris, S Africa.

Hello again,

I have another probability question that i hope you can answer for me.

On a Punto banco game what are the probs of a standoff (Egalite) of 0 thru 9

Ie: 10 probs in total.

Thanks in advance.

Chris.

Quote: ChrisSA

Hello again,

I have another probability question that i hope you can answer for me.

On a Punto banco game what are the probs of a standoff (Egalite) of 0 thru 9

Ie: 10 probs in total.

Thanks in advance.

Chris.

See Egalite Bets

Thank you so much.

Chris