Three Card Joker Poker

I'm working on a new game and some of the math is making my head hurt. So thinking it might help, I asked ChatGPT some preliminary questions and got a really questionable answer.

Question: With a standard 52 card deck plus 1 joker, how many ways are there to deal a straight flush.

This seemed pretty simple to me.

ChatGPT said that there are 12 combinations of A23 thru QKA, times 4 suits = 48, and 6 ways of dealing 3 cards = 288, and I agreed.

ChatGPT said that since any card could be substituted by the joker, there are 288 * 3 ways to deal 3 cards, so 864 combinations of a wild straight flush. I get that simple logic, but is it too simple?

I'm thinking there are 13 two card combinations, A2 thru KA which could be a wild SF when a joker is added, plus 12 gapped combinations, A3 thru QA, which become a wild SF when the joker fills the gap. 25 * 4 suits, * 6 ways to deal 3 cards = 600.

Essentially, ChatGPT is counting two consecutive cards like 3 4 Joker twice - where the joker is either end - a 2 or a 5.

Can someone please confirm one of these methods, because the next step of my game idea - the part where I really need the help - gets really crazy.

FYI: In Excel I have:
Straight Flush = 12 * 4 * 6 = 288 (As above, 12 combinations, 4 suits, 6 ways to deal them)
Wild SF = 25 * 4 * 6 = 600 (25 combinations, 4 suits, 6 ways to deal)
Straight = 12 * 4 * 4 * 4 * 6 - 288 = 4320 (Each card can be any suit, but subtract the straight flush count)
Wild Straight = 25 * 4 * 4 * 6 - 600 = 1800 (The last card is a joker and there's only one)

Thanks.

It looks like your method is right. Just as you said, ChatGPT is counting 3, 4, Joker twice - once as one of the orders if the Joker represents a 2, and once as one of the orders if it represents a 5.

I agree with ThatDonGuy. Double counting is the bane of poker hand analysts, and ChatGPT fell into the trap.

Your math is right. Just wondering why you are multiplying all the hand types by 6 if the order in which the cards are drawn doesn't matter. Strictly speaking, combinations count things where order doesn't matter and permutations count things where order does matter. I believe you could simplify all your math by omitting the factor of 6.

Good luck with the game!

Thanks for the replies.

I'm gonna have a follow up question soon.

Quote: rackuun

... Just wondering why you are multiplying all the hand types by 6 if the order in which the cards are drawn doesn't matter. ...link to original post

Because I DO want to count every sequence of dealing. It makes certain numbers far easier to calculate.

For example, a natural three of a kind is 13 * 4 * 3 * 2: 13 ranks, 4 suits, 3 suits, 2 suits. It already accounts for every combination of dealing each rank of trips.

Additionally, "nothing" or "other" is merely the total combinations less the number of combinations of each defined hand. The easiest way to get the total combinations (which is also needed when calculating house edge), without the joker, is 52 * 51 * 50, or with the joker its 53 * 52 * 51.

Plus, because I don't trust my math (High School P&S class was a long time ago), I'm running a program to loop thru every combination, examine the results and total it up. And one of my numbers is off just a little. I'm not sure if the error is in my Excel formula or in my program. And I've been beating up both for days now trying to figure it out.

The reason I asked these questions is because of a new game that I created.

Pick A Suit

I just put up a post about it:

https://wizardofvegas.com/forum/gaming-business/game-inventors/40071-pick-a-suit/

Please keep discussions about the Math on this thread while discussions about the game itself should be on the other thread.

Thanks.

I didn’t check the jackpot pay table, but the other 2 are correct as far as I can tell.

Here are the calculations I've made based on a standard deck and then adding a Joker as any rank. In the latter case there are, for instance if you've bet Aces, Five Aces and 48 duds. Also it's nice the payout for one winner can be 2 to 1 instead of 3 to 1 to keep a similar House Edge. (Note I've used 50/1 since it's nicer!)

No jokers
A A A	4	Four aces	50
A A x	288	4x3/2 * 48	10
A x x	4 512	4 x 48*47/2	3
x x x	17 296	48*47*46/6	- 1
	22 100		-3.077%

Jokers
A A A	10	10	50
A A x	480	5x4/2 * 48	10
A x x	5 640	5 x 48*47/2	2
x x x	17 296	48*47*46/6	- 1
	23 426		-3.056%

Ways of making a SF can be considered by thinking of its highest card. Thus with AKQ think A, KQJ=K...until 32A think 3. Therefore the highest card could be A K Q .... 3 but can't be any 2. This gives 48 cards with an associated SF.

With a joker the other two cards have to be adjacent or one gap apart.
(a) Every card in the pack could have its adjacent card (AK...32,2A). this gives 52 ways.
(b) The other is one-gap (e.g. AQ, KJ etc.). As earlier this can be A K Q .... 3 but can't be a 2. Hence this gives 48 ways.
The total is therefore 100.

I should have posted this sooner.

Figuring out the three card hands, including those that are wild, wasn't that tricky. And the program I wrote to cycle thru every combination and analyze it gave me the same results (once I eliminated a couple typos / bugs).

It's the fourth card math that is driving me nuts. Specifically, the number of times a wild three card straight flush becomes a straight.

Here's a portion of my Excel document. Note that each color section represents a single payline on my other documentation. It's line H (and N) that is giving me grief.



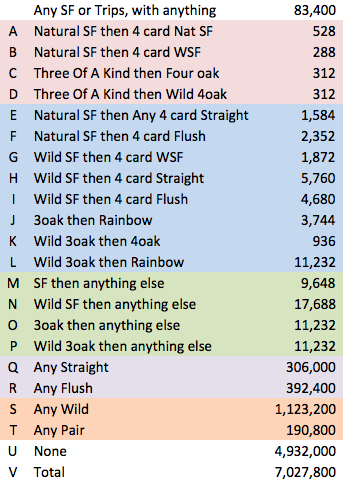
Mind you the number of times it becomes a four card straight flush, I got my Excel and program to agree on.

But every time I think about adjusting the Excel calculation, I come up with a lower number, and it's ALREADY slightly lower than what the program says.

And considering that my program uses the same logic for both, I kinda think my Excel math is wrong.

Quote: DJTeddyBear

...It's the fourth card math that is driving me nuts. Specifically, the number of times a wild three card straight flush becomes a straight....

I suspect the easiest way is to consider the number of outs for the various possibilities.
(a) Consider adjacent cards with a Joker
(i) AK, A2 - two outs [ranks] (QJ or 34) (so two cards are SF, six cards are straight).
(ii) KQ, 32 - three outs (AJT, A45)
(iv) QJ...43 - four outs (AKT9, 652A)
(b) Consider one-gaps with a Joker
(ii) AQ, A3 - two outs
etc.

Quote: charliepatrick

I suspect the easiest way is to consider the number of outs for the various possibilities...
link to original post

I had read Charlie's post several times but didn't understand what he was trying to say.

But I finally figured out how to correctly calculate the number of combinations of 3 cards Wild Straight Flushes that improve to a 4 card Wild Straight Flush. And Charlie was spot on, but I just couldn't see it until I penciled it out myself.


Here's the long version:

While I kept improving my program by getting rid of tiny errors, for days I couldn't find any new errors even thoguh it still didn't match my Excel numbers. Then I realised that in my program, I was finding every different type individually, but in Excel I was generalizing.

Calculating a Wild Straight Flush is easy. 13 connected combos or 12 gapped combos, plus a joker. That's 25 combinations. Times 6 ways to deal them and 4 suits. 25*6*4 = 600 simple.

Surely, calculating the improvement was equally simple. After all, calculating a wild Three of a Kind and all the ways it could improve was simple.

Bottom line, that was the error. It's not so simple or straight-forward.

The thing is some wild straight flushes have two outs to improve, some have three and some have four. I need to count them all individually.

It took a while to realize that. The result is there are a total of 80 types and ranks once improved.

To illustrate, there are 13 ranks of two suited connected cards with a joker that are wild straight flush. They are A2 thru KA.

Of those, A2 and KA will improve with either of two cards: A2 plus either 3 or 4, KA plus either of J or Q.

Similarly, 23 and QK can improve with 3 cards: 23 plus A, 4 or 5 and QK plus T, J or A.

Lastly, 34 thru JK can improve with and of 4 cards: 34 can get A, 2, 5 or 6, etc.

That totals 46 ways to improve connected wild straight flushes.

Similar logic applies to 12 ranks of gapped wild straight flushes.

A3 and QA can improve with two cards: A3 can get 2 or 4 while the QA can get J or K.

24 thru JK can improve with three cards: 24 can get A, 3 or 5 while JK can get T, Q or A, etc.

That's 34 ways to improve the gapped wild straight flush.

So the answer is 80 different types and ranks. Multiply that by the 6 ways to deal the first 3 cards, times 4 suits.

Multiply that number times 3 for the number of times it improves to a straight, but not a straight flush.

That done, all my numbers match the numbers produced by my program.

The house edge, when rounded to the standard of one decimal place, didn't change. I predicted this when I first started this thread. And now just minor updates one web page and the last page of the PDF description, which I uploaded just a few minutes ago.

I'm a happy camper.