Poll
 | 4 votes (33.33%) | ||
 | 5 votes (41.66%) | ||
| No votes (0%) | |||
 | 4 votes (33.33%) | ||
 | 1 vote (8.33%) | ||
| No votes (0%) | |||
 | 1 vote (8.33%) | ||
 | 1 vote (8.33%) | ||
 | 4 votes (33.33%) | ||
 | 3 votes (25%) |
12 members have voted
Quote: Mental
It would be nice to confirm that the game can go directly from 12x to 2x on the next hand. If there was one dead hand after every bonus round, our models would be far off the mark.
You can in fact get the next bonus round started immediately after the previous one ends. It happens 10.96% of the time. Not only can a 2x occur immediately after a 12x, but a 2x can occur after cashing in an intermediate multiplier of 2x, 3x, 5x, or 8x.
Quote: WizardSo, a rather crude spreadsheet YH gave me shows a feature probability of 11%. I questioned him on the difference with the 10.96% on the game screen and he said something to the effect of 10.96% being an average over multiple different games.
If he was implying that the DDB game is actually 11%, while other games' averages make some overall average equal to 10.96%, I would think that the HELP screen for DDB should say 11%. At least at videopoker.com, all the Fortune X DDB games do say 10.96%.
I then calculate the RTP of the game via a billion game MC simulation two times with just one difference.
(A) I set the last cutoff point just below this neutral value, NV. This terminates the bonus round whenever the 'deal' comes up with the EV equal to the NV.
(B) I set the last cutoff point just above NV. This extends the bonus round whenever the 'deal' comes up with the EV equal to the NV. Bonus rounds are thus less frequent.
Anyone care to guess how the RTPs compare? Is the RTP higher under scenario (A) than under scenario (B), lower, or the same?
Quote: MentalI did a new calculation with a substantially simpler game of my own creation. I designed the game to have a cutoff value for the last decision point that is exactly neutral to the EV for a vulture (NV). In other words, a vulture could get the same absolute EV by accepting the penultimate multiplier or by playing at 1X and then taking the forced multiplier on the next game.
I then calculate the RTP of the game via a billion game MC simulation two times with just one difference.
(A) I set the last cutoff point just below this neutral value, NV. This terminates the bonus round whenever the 'deal' comes up with the EV equal to the NV.
(B) I set the last cutoff point just above NV. This extends the bonus round whenever the 'deal' comes up with the EV equal to the NV. Bonus rounds are thus less frequent.
Anyone care to guess how the RTPs compare? Is the RTP higher under scenario (A) than under scenario (B), lower, or the same?
link to original post
I'm not certain that I understand how "substantially simpler" the game is, or exactly what the rules are. However, if you have a cutoff that is optimal in a game like Fortune X, and you either increase the cutoff by a bit to induce more declines of the current multiplier or decrease the cutoff by a bit to get more acceptances of the current multiplier, two things can happen. The one thing that cannot happen is that the return increases. If the return increases, your cutoff was not optimal, whether you have designed it to be neutral or not.
However, it is certainly possible that a small increase or decrease in the cutoff could leave the return exactly the same, or it could decrease the return.
I will illustrate, using the actual game we have been analyzing as an example.
The cutoffs calculated by the Wizard differed from those calculated by the method I used. And I don't know whether YH's cutoffs were the same as mine even though both sets produced identical EVs.
| Mult | Wizard | DrRock | Difference | LoHandEV | HiHandEV | InBetween |
|---|---|---|---|---|---|---|
| 2x | 8.901087 | 8.982528 | 0.081441 | 7.530990 | 9.000000 | 0 |
| 3x | 4.88974 | 4.919957 | 0.030217 | 4.000000 | 5.366327 | 0 |
| 5x | 2.567263 | 2.577339 | 0.010076 | 2.531915 | 3.53195 | 0 |
| 8x | 1.411099 | 1.414317 | 0.003218 | 1.407956 | 1.421832 | 3312 |
For some reason, my cutoffs are always higher than the Wizard's in this example. LoHandEV shows the EV of the hands that have the highest EV that are still below the Wizard's cutoff. HiHandEV shows the EV of the hands that have the lowest EV that are still above my cutoff.
I don't know what interest there might be, but if you are going to play this game, it would be important for you to translate these cutoffs and EVs into actual hands.
For 2x, you decline the multiplier for trips 2s-4s and below, while accepting it for a full house and above.
For 3x, you decline the multiplier for dealt straights and below, while accepting it for trip 5s-Ks and above.
For 5x, you decline the multiplier for KQJ9 suited and below, while accepting it for 4-card open-ended straight flush draws and above.
For 8x, you decline the multiplier for KJT,KQT,AJT,AQT,AKT suited 3-card Royals and below, while accepting it for pairs of Js-Ks, and QJT or KQJ suited 3-card Royals and above.
Note that the smallest difference in cutoffs is with 8x, but that is the only difference that has any effect. On the other hand, the relatively larger differences with the other cutoffs have zero effect because there are zero hands that have an EV between the Wizard's cutoffs and mine. The wider differences for 2x, 3x, and 5x, produce no difference at all; for 8x, there are 3312 hands that have an EV of 1.411656, higher than the Wizard's cutoff and lower than mine. My cutoff says to forgo the 8x multiplier and wait for the next hand and 12x. The Wizard's cutoff says to accept the 8x multiplier for these hands.
Do I know whether my cutoff calculations are perfectly correct? Well, I used unrounded data in some cases so, no. I could also have made some arithmetic mistakes. But for these calculations, you could get lucky and get optimal results even without optimal cutoffs.
The holds in between the Wizard's 8x cutoff and mine are all 3-card Royals of the form AQJ, AKJ, or AKQ suited with the other two cards not the same suit as the RF cards and of ranks 2 through 9. Their EV is 1.411656, ever so slightly higher than the Wizard's cutoff, but below mine.
So is such a tiny difference significant? Here, not much since the game EV increases by only 0.0001% if you use my 8x cutoff instead of the Wizard's, decline 8x on these hands and try the next hand for 12x.
But in this thread the Wizard showed that YH's using 11% instead of 10.96%, a difference of only 0.04% ended up making a difference from 98.97% to 99.01%, a difference of 0.14%, more than tripling the effect of the tiny difference. So you never know until you are certain that your methodology captures the highest possible EV.
Getting back to Mental's question, so long as the space between different cutoffs contain no hands having EVs between them, there will be no difference in EV by moving the cutoff. However, if you move an optimal cutoff up or down, you cannot get a better than optimal result, and you might get a worse one.
I agree. Webman is the best. I never had the opportunity to meet their previous mathematician or YH, but they seem to be top-notch as well.Quote: Wizard... I love everybody there [VideoPoker.com] and thank them very much for all their cooperation through the years ...
Very nice! I actually don't care much about the Fortune X Poker game itself. I just think it offers a great problem for sharpening my intuition about these sorts of games that offer novel strategy choices. I have learned a lot by interacting with everyone on this thread, especially Wiz and drrock. These discussions involved some some neat math tools that might be very useful in the future.Quote: WizardI just updated my Fortune X page to show detailed calculations, that arrive at the 99.01% RTP. I fully agree if the feature probability is 11.00%, then that is what the rules screens should say. However, I hope I won't get anybody upset if I say in public they can be a little lazy in getting their rule screens correct at VideoPoker.com. The third page in their rules seems to be for a totally different game. However, I love everybody there and thank them very much for all their cooperation through the years and hope if they read this they will file it under peer review.
link to original post
Someone once told me that a MP is a machine player who has been told the cutoff values for a play and simply plays the machine. An AP is someone who can accurately calculate the cutoff values. I strive to be an AP.
The, "Indifference," EV is especially useful to vultures, some of whom, I would assume, would otherwise be inclined to just take any multiplier as long as the deal isn't total garbage.
Quote: MentalI did a new calculation with a substantially simpler game of my own creation. I designed the game to have a cutoff value for the last decision point that is exactly neutral to the EV for a vulture (NV). In other words, a vulture could get the same absolute EV by accepting the penultimate multiplier or by playing at 1X and then taking the forced multiplier on the next game.
I then calculate the RTP of the game via a billion game MC simulation two times with just one difference.
(A) I set the last cutoff point just below this neutral value, NV. This terminates the bonus round whenever the 'deal' comes up with the EV equal to the NV.
(B) I set the last cutoff point just above NV. This extends the bonus round whenever the 'deal' comes up with the EV equal to the NV. Bonus rounds are thus less frequent.
Anyone care to guess how the RTPs compare? Is the RTP higher under scenario (A) than under scenario (B), lower, or the same?
link to original post
Snipped from a much longer response from drrock:
You may have missed my point: The NV EV is the EV after the deal where a vulture gets the same EV for accepting or declining the penultimate multiplier. Either choice is optimal for EV. Declining leads to a different variance, but the same expected monetary gain. The question is if the RTPs are the same for playing the game through many cycles.Quote: drrockGetting back to Mental's question, so long as the space between different cutoffs contain no hands having EVs between them, there will be no difference in EV by moving the cutoff. However, if you move an optimal cutoff up or down, you cannot get a better than optimal result, and you might get a worse one.
It took me a while to create a game where I could easily get a vulture EV that was exactly neutral. My made-up game is just the familiar beat-the-dealer game (BTD) used in the VP double-up feature. My BTD game requires one bet for all games. The dealer draws one card randomly from 10 cards ranked 1 to 10. The player draws one card from an identical 10-card deck. The player pushes if their card is higher than the dealer card, otherwise the player loses. The EV of a normal game is just 45% before the deal. When the dealer draws a 10, the EV drops to 0%. When the dealer draws a 1, the EV rises to 90%. Once in 25 games, the 2x bonus is offered. This starts a sequence of 2x,3x,5x,20x, and 36x multiplier using the Fortune X rules.
If I did the math right, the player always rejects all but the 20x multiplier. If the dealer draws a 1, the player accepts the 20x multiplier. If the dealer draws a 2 and, the player accepts the 20x multiplier, then they have a 80% chance of beating the dealer. The EV is 0.8 * 20 = 16. If they decline the 20x, then they pay another bet and get an expected return of 0.8 from the current game and (0.45 * 36) - 1 from the final bonus game for a return of 16. This means 0.8 on the deal is neutral to the vulture (NV=0.8).
I present four tables with four values of the cutoff EV. Each is a billion game MC simulation. The first table uses a cutoff EV of 0.95, which is higher than any possible dealer card. Therefore, no optional multiplier is ever accepted and the bonus round always goes to the last forced multiplier. The RTP at the bottom of the table (99.3009% RTP) can be calculated by noting that each bonus cycle has 28 games paid back at 1 * 0.45 and one game with 36 * 0.45. (28*0.45+36*0.45) / 29. = 99.3103%.
| Mult | Visit | Accept | Collect | RTP |
|---|---|---|---|---|
| 1 | 0.82762 | 1.00000 | 0.96552 | 0.45000 |
| 2 | 0.03448 | 0.00000 | 0.00000 | 0.45005 |
| 3 | 0.03448 | 0.00000 | 0.00000 | 0.45001 |
| 5 | 0.03448 | 0.00000 | 0.00000 | 0.44996 |
| 20 | 0.03448 | 0.00000 | 0.00000 | 0.44996 |
| 36 | 0.03448 | 1.00000 | 0.03448 | 16.20037 |
| 0.95 | Cutoff | 99.3009% | RTP |
The Visit column gives the fraction of times that a game visits the multiplier in the Mult column. The Accept column gives the fraction of times we accept an offered multiplier. We always accept 1x and 36x. The Collect column gives the percentage of times that the payoff that we would collect if we won would be multiplied by that Mult. The RTP column gives the return to player when the Mult is offered. (36 * 0.45 = 16.2)
| Mult | Visit | Accept | Collect | RTP |
|---|---|---|---|---|
| 1 | 0.83044 | 1.00000 | 0.96540 | 0.44999 |
| 2 | 0.03460 | 0.00000 | 0.00000 | 0.44998 |
| 3 | 0.03460 | 0.00000 | 0.00000 | 0.45001 |
| 5 | 0.03460 | 0.00000 | 0.00000 | 0.44998 |
| 20 | 0.03460 | 0.10001 | 0.00346 | 2.16012 |
| 36 | 0.03114 | 1.00000 | 0.03114 | 16.19977 |
| 0.85 | Cutoff | 99.9676% | RTP |
| Mult | Visit | Accept | Collect | RTP |
|---|---|---|---|---|
| 1 | 0.83333 | 1.00000 | 0.96528 | 0.45000 |
| 2 | 0.03472 | 0.00000 | 0.00000 | 0.45011 |
| 3 | 0.03472 | 0.00000 | 0.00000 | 0.44996 |
| 5 | 0.03472 | 0.00000 | 0.00000 | 0.45006 |
| 20 | 0.03472 | 0.20004 | 0.00695 | 3.68061 |
| 36 | 0.02778 | 1.00000 | 0.02778 | 16.20220 |
| 0.75 | Cutoff | 99.9727% | RTP |
| Mult | Visit | Accept | Collect | RTP |
|---|---|---|---|---|
| 1 | 0.83622 | 1.00000 | 0.96515 | 0.45001 |
| 2 | 0.03485 | 0.00000 | 0.00000 | 0.45001 |
| 3 | 0.03485 | 0.00000 | 0.00000 | 0.44999 |
| 5 | 0.03485 | 0.00000 | 0.00000 | 0.45005 |
| 20 | 0.03485 | 0.30004 | 0.01046 | 5.01069 |
| 36 | 0.02439 | 1.00000 | 0.02439 | 16.19799 |
| 0.65 | Cutoff | 99.3045% | RTP |
The RTPs are essentially the same for a cutoff of 0.75 or 0.85. These are above and below the NV of 0.8. I had expected a difference. I followed up with forty 1B sims for each and the RTPs are identical within the std. dev. of 0.01%. The bonus frequency is slightly shorter for 0.75 because we are accepting the 20x multiplier two times out of ten that it is offered. I may need to work through this analytically to see if the RTPs are exactly equal.
Given
I am at the 8X multiplier level and have been dealt a hand of AQJ suited that has an EV of 1.411656 – above the Wizard’s threshold level of 1.41109914. I have to decide whether to accept or reject the 8x multiplier.
In this scenario, we will consider the value of the next two dealt hands no matter the decision on multipliers. This is equivalent to the situation in a simulation of a set number of trials, as if a player has made a decision to play a certain number of hands no matter what decisions are made.
The trade-off:
If I reject the 8x multiplier:
- I will default to a 1x multiplier on my current hand. My current hand has a value of 1.411656 on a 5 unit bet or 1.411656 *5 = 7.05838 units
- I will pay 10 units to be dealt a new hand with a 12x multiplier.
- My new hand has a value of 5 (units) *0.989808 (per unit) * 12 = 59.38848
- Summing: 7.05838 -10 + 59.38848 = 56.44676 (value in units)
If I accept the 8x multiplier:
- My current hand has a value of 8*1.411656 = 11.29325 per unit; on the 5 units counted as a wager this is an expected value of 56.46624 units (round to 56.466).
- I will pay 10 units to be dealt a new hand with a 1x multiplier.
- My next hand, at a multiplier of 1x has an immediate payout value of 0.989808/2 *5 = 2.47452. If we consider the 1/11 chance of triggering the bonus multiplier feature, it has an imputed value of 0.9901*10 = 9.901.
So the total value of accepting the multiplier, including the imputed value, is 56.466 -10 +9.901 = 56.367
Conclusion
Thus, when using an “equal number of hands played” rule (equivalent to a simulation)
Accepting 8x mult. Has a value of 56.367
Rejecting 8x mult. Has a value of 56.447.
So, when considering the subsequent dealt hand for both options, rejecting the 8x multiplier has more value for AQJ(suited) even though AQJs has an EV value above the Wizard’s threshold. I believe this has been Mental's point, and what drrock may be trying to test with his simulation.
Quote: gordonm888Illustration of the point being discussed
Given
I am at the 8X multiplier level and have been dealt a hand of AQJ suited that has an EV of 1.411656 – above the Wizard’s threshold level of 1.41109914. I have to decide whether to accept or reject the 8x multiplier.
In this scenario, we will consider the value of the next two dealt hands no matter the decision on multipliers. This is equivalent to the situation in a simulation of a set number of trials, as if a player has made a decision to play a certain number of hands no matter what decisions are made.
So, when considering the subsequent dealt hand for both options, rejecting the 8x multiplier has more value for AQJ(suited) even though AQJs has an EV value above the Wizard’s threshold. I believe this has been Mental's point, and what drrock may be trying to test with his simulation.
link to original post
The points you are illustrating are essentially correct. The method I use look at the difference in the next 25 or so hands, following the rules of the game, not the next 2. Actually, the method looks at the difference in the limit of the all the hands in the future with unlimited play, but practically, after 25 hands or so, the differences decay to essentially zero.
On the last point I highlighted, I think you just have our usernames switched. Mental has been doing all the simulations.
Quote: Mission146I'm confused; if the player accepts the 8x multiplier, why is the assumption that he must play a hand after that one? While the player probably will, in most cases, the vulture would not.
link to original post
The distinction between a "vulture" cutoff and a continuous-play cutoff is subtle. And it is possible that they are identical in some instances, but they do not need to be.
All the calculations that I have been doing have been to select the correct cutoffs for continuous play, not with respect to vulturing. One of the purposes here was to calculate the EV for the game. There would be slightly different calculations for vulturing. Also, you are not simply calculating a single cutoff for 8x. You are calculating a set of 4 multipliers simultaneously {2x, 3x, 5x, 8x}. Each of the cutoffs are interdependent on the others.
To that point, I imagine that some players may leave these games with a multiplier string active because they run out of money. There are always people playing games who have little idea what they are doing. I get that. However, this game typically has much more value vested in the bonus round such that it would be really silly to leave it at that point. Pretty much, this would be pretty similar to leaving a multihand Ultimate X game right after getting a dealt full house and leaving a tableau full of 12x's on the board. With 10-play Ultimate X, you have multipliers on virtually every hand, so it is not that uncommon that someone might see these as ho-hum and leave. But on this game, not only are the multipliers rare, but the whole point of the game is that the multiplier may be rising on each hand after the first one appears. If you play the game a while, maybe you'll come to the same conclusion that I have, but maybe your experiences with observing people who have little idea what their doing is more accurate than what I think might happen with this game.
All that being said, if the intention is to leave exactly after a given bonus round finishes, the cutoff values could be slightly different not only for 8x but also for the other 3 that preceded it. That actually is a much simpler calculation.
The calculations that have been discussed in this thread by me take into consideration that if you finish the current bonus round early, the next one will start earlier.
Quote: MentalYou may have missed my point: The NV EV is the EV after the deal where a vulture gets the same EV for accepting or declining the penultimate multiplier. Either choice is optimal for EV. Declining leads to a different variance, but the same expected monetary gain. The question is if the RTPs are the same for playing the game through many cycles.
Hey, Mental. Interesting brain-twister. It took me several readings to fully understand what you were trying to say here. I certainly did not know the particulars of the game that you had in mind with my first response, but before addressing the exact game that you are now outlining, I will first repeat what I said in my original response to you:
"However, if you have a cutoff that is optimal in a game like Fortune X, and you either increase the cutoff by a bit to induce more declines of the current multiplier or decrease the cutoff by a bit to get more acceptances of the current multiplier, two things can happen. The one thing that cannot happen is that the return increases. If the return increases, your cutoff was not optimal, whether you have designed it to be neutral or not."
This still stands for the game that you have clarified here.
The key here is not whether the optimal cutoff is also neutral for a vulture. Whether you are above or below optimal is what is important, not whether or not the cutoff is also vulture-neutral.
A side note: As you might have seen in my previous response to Mission and Gordon, the vulture's optimal cutoffs, whether knife-edge neutral or not, actually will in practice be different than the optimal cutoffs for maximizing EV with continuous play. It is possible given that the step function like the one you outlined for me of the possible hand EVs is such that the cutoffs for both vulture and continuous play could be equal, and they will probably be fairly close, but they are not guaranteed to be equal.
The calculation for an optimal vulture cutoff considers only the hands up to the end of the current bonus round. The continuous-play optimal cutoff considers also the hands after the bonus round, the most important aspect of this is how soon the next bonus round can start.
The game that you designed is an excellent example for what is above. I get that the game you designed has a cutoff of a dealer card of 2 allows a vulture the same EV whether he accepts a 20x and stops or passes on the 20x, invests one more bet and takes a shot at 36x.
And I can see that you did a billion simulations for various cutoffs. Unfortunately, the analytical EVs on this game are so close that you will not be able to determine via simulation whether for continuous play (which is what a billion-rep simulation is imitating), which cutoff is better than the other, whether there is a small difference between EVs or a difference of zero. And if there is a difference, which cutoff produces the larger EV.
On your game, for continuous play, it turns out the optimal EV occurs when you accept 20x ONLY when the dealer's card is 1. When you do that, the game EV is 0.9996540. When you have the policy of accepting 20x also on dealer cards of 2 (as well as 1), the game EV drops ever so slightly to 0.9996528. I could include a few more decimal places since Excel generally keeps 14 or 15, but it would be tough to expect a simulation to be able to tell the difference between these two EVs. I could also supply exact numbers corresponding to what your simulations were estimating, but that will have to wait, at least for now.
If you think of the acceptance percentage for a particular multiplier as a step function, you will see that with your game, the only percentages that make sense are 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, or 100%. Sure you can come up with something like 16% where you would accept when the dealer has a 1 and 60% of the time when he has a 2, but you will be incredibly lucky for that to be optimal. Of course, you could also be technically correct by saying you will accept the 20x multiplier when the dealer's card is less than or equal to 1.6, but that is only because there is no possibility of a dealer card being in the open interval (1,2).
I am confused as to why you are even interested in the vulturing RTP. It is big enough in any case. I make roughly 0% of my income by vulturing games. I make it by finding long plays with RTP + bennies > 100%. We are trying to determine the long term RTP. I am trying to figure out if a neutral EV vulture multiplier should be generally be accepted by a long term player or not.Quote: Mission146I'm confused; if the player accepts the 8x multiplier, why is the assumption that he must play a hand after that one? While the player probably will, in most cases, the vulture would not.
link to original post
Quote: drrockQuote: MentalYou may have missed my point: The NV EV is the EV after the deal where a vulture gets the same EV for accepting or declining the penultimate multiplier. Either choice is optimal for EV. Declining leads to a different variance, but the same expected monetary gain. The question is if the RTPs are the same for playing the game through many cycles.
Hey, Mental. Interesting brain-twister. It took me several readings to fully understand what you were trying to say here. I certainly did not know the particulars of the game that you had in mind with my first response, but before addressing the exact game that you are now outlining, I will first repeat what I said in my original response to you:
"However, if you have a cutoff that is optimal in a game like Fortune X, and you either increase the cutoff by a bit to induce more declines of the current multiplier or decrease the cutoff by a bit to get more acceptances of the current multiplier, two things can happen. The one thing that cannot happen is that the return increases. If the return increases, your cutoff was not optimal, whether you have designed it to be neutral or not."
This still stands for the game that you have clarified here.
The key here is not whether the optimal cutoff is also neutral for a vulture. Whether you are above or below optimal is what is important, not whether or not the cutoff is also vulture-neutral.
A side note: As you might have seen in my previous response to Mission and Gordon, the vulture's optimal cutoffs, whether knife-edge neutral or not, actually will in practice be different than the optimal cutoffs for maximizing EV with continuous play. It is possible given that the step function like the one you outlined for me of the possible hand EVs is such that the cutoffs for both vulture and continuous play could be equal, and they will probably be fairly close, but they are not guaranteed to be equal.
The calculation for an optimal vulture cutoff considers only the hands up to the end of the current bonus round. The continuous-play optimal cutoff considers also the hands after the bonus round, the most important aspect of this is how soon the next bonus round can start.
The game that you designed is an excellent example for what is above. I get that the game you designed has a cutoff of a dealer card of 2 allows a vulture the same EV whether he accepts a 20x and stops or passes on the 20x, invests one more bet and takes a shot at 36x.
And I can see that you did a billion simulations for various cutoffs. Unfortunately, the analytical EVs on this game are so close that you will not be able to determine via simulation whether for continuous play (which is what a billion-rep simulation is imitating), which cutoff is better than the other, whether there is a small difference between EVs or a difference of zero. And if there is a difference, which cutoff produces the larger EV.
On your game, for continuous play, it turns out the optimal EV occurs when you accept 20x ONLY when the dealer's card is 1. When you do that, the game EV is 0.9996540. When you have the policy of accepting 20x also on dealer cards of 2 (as well as 1), the game EV drops ever so slightly to 0.9996528. I could include a few more decimal places since Excel generally keeps 14 or 15, but it would be tough to expect a simulation to be able to tell the difference between these two EVs. I could also supply exact numbers corresponding to what your simulations were estimating, but that will have to wait, at least for now.
If you think of the acceptance percentage for a particular multiplier as a step function, you will see that with your game, the only percentages that make sense are 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, or 100%. Sure you can come up with something like 16% where you would accept when the dealer has a 1 and 60% of the time when he has a 2, but you will be incredibly lucky for that to be optimal. Of course, you could also be technically correct by saying you will accept the 20x multiplier when the dealer's card is less than or equal to 1.6, but that is only because there is no possibility of a dealer card being in the open interval (1,2).
link to original post
Great response.
Yes, I always understood that moving cutoffs through the gaps makes no difference in the RTP. It changes no decisions.
You can see that my acceptance percentages fall in the table on the 10% intervals as expected.
I agree that if the optimal long-term cutoffs are changed, the RTP must stay the same or decrease. This what optimal means.
I was not talking about this. I was asking whether long-term RTP changes when you move the cutoff through a neutral vulture EV (Wiz says vulture indifferent EV). If the RTP changes, is the optimum cutoff above or below this special EV? In a VP game, you will probably never find such a lucky neutral EV. That is why I invented a simple game where this is a special neutral EV value. I failed spectacularly in creating a game where there is a clear difference moving the cutoff through the vulture indifferent EV. I thought for sure there would be a clear answer one way or the other.
Quote: MentalI am confused as to why you are even interested in the vulturing RTP. It is big enough in any case. I make roughly 0% of my income by vulturing games. I make it by finding long plays with RTP + bennies > 100%. We are trying to determine the long term RTP. I am trying to figure out if a neutral EV vulture multiplier should be generally be accepted by a long term player or not.Quote: Mission146I'm confused; if the player accepts the 8x multiplier, why is the assumption that he must play a hand after that one? While the player probably will, in most cases, the vulture would not.
link to original post
link to original post
Fair enough! In any case, this wouldn’t be my game of choice for long-term play; the variance must be obscene.
Hmmmm....Quote: MentalI was asking whether long-term RTP changes when you move the cutoff through a neutral vulture EV (Wiz says vulture indifferent EV). If the RTP changes, is the optimum cutoff above or below this special EV? In a VP game, you will probably never find such a lucky neutral EV. That is why I invented a simple game where this is a special neutral EV value. I failed spectacularly in creating a game where there is a clear difference moving the cutoff through the vulture indifferent EV. I thought for sure there would be a clear answer one way or the other.
link to original post
I am not 100% certain, but what we have seen here thus far is that continuous-play optimal cutoffs have been more exclusive than vulture optimal cutoffs, again whether these happen to be your definition of vulture-neutral or not. By "more exclusive," I mean the multiplier acceptance probability will be lower (or, in the cases where there is no difference, at least not higher).
And I can say that is what happened in the game you invented as well, though the EVs were so, so close.
I think that the Wizard's calculation methods were very close if not equivalent to calculating vulture optimal cutoffs. I know that is what I used as initial values for cutoffs to feed into the iterative method that I used to determine what I thought should be continuous-play optimal cutoffs.
Those are the only examples that I have explored.
Other things to ponder: Is it possible to have two different consecutive hands on our spectrum that using either as a cutoff will imply the same EV? I don't know. Could slight differences in your game accomplished this? Again, I don't know. With marketable video poker games, I think it is unlikely but not 100% impossible I suppose.
Even if we figure out that games that we may define as substantially similar to Fortune X always work in a particular manner, there may be some (even minor) alteration that causes the behavior of the relationship to differ from what we see here.
Quote: Mission146Quote: MentalI am confused as to why you are even interested in the vulturing RTP. It is big enough in any case. I make roughly 0% of my income by vulturing games. I make it by finding long plays with RTP + bennies > 100%. We are trying to determine the long term RTP. I am trying to figure out if a neutral EV vulture multiplier should be generally be accepted by a long term player or not.Quote: Mission146I'm confused; if the player accepts the 8x multiplier, why is the assumption that he must play a hand after that one? While the player probably will, in most cases, the vulture would not.
link to original post
link to original post
Fair enough! In any case, this wouldn’t be my game of choice for long-term play; the variance must be obscene.
link to original post
Fortune X would not be my game of choice because it is -EV and I would not expect to get 2% bounce back on the game. I don't go looking for variance, but we clearly have different ideas of how much variance it takes to qualify as obscene. I recently lost $40K before breakfast and I just chalked it up to 'shit happens'.
Quote: drrockAnd I can see that you did a billion simulations for various cutoffs. Unfortunately, the analytical EVs on this game are so close that you will not be able to determine via simulation whether for continuous play (which is what a billion-rep simulation is imitating), which cutoff is better than the other, whether there is a small difference between EVs or a difference of zero. And if there is a difference, which cutoff produces the larger EV.
On your game, for continuous play, it turns out the optimal EV occurs when you accept 20x ONLY when the dealer's card is 1. When you do that, the game EV is 0.9996540. When you have the policy of accepting 20x also on dealer cards of 2 (as well as 1), the game EV drops ever so slightly to 0.9996528. I could include a few more decimal places since Excel generally keeps 14 or 15, but it would be tough to expect a simulation to be able to tell the difference between these two EVs.
Your analytical numbers are really helpful to me. I am impressed that you could plug my rules into your system of equations so quickly.
I subtracted 1.0 from each of your RTP numbers to convert them from RTPs to EVs. This makes the relative differences larger.
-0.0003472 / -0.0003460 = 1.00347
(I am always putting the 0.75 cutoff EV first and the 0.85 cutoff second in the comparison.)
So, it appears to me that I set up my BTD game EV too close to 100% RTP. This made the delta too small to discriminate with my MC sim. If I change the bonus to trigger one game in 30 (versus 25), I immediately widen the gap in EVs to
-0.08167 / -0.08140 = 1.00327
and I can easily tell which EV is greater with 10B simulated games.
Now, if I change the bonus to trigger one game in 20, the EV become positive (111% RTP).
0.11512 / 0.11469 = 1.00379
The ratio is similar to the other ratios, but because the numbers are positive, this means the sign of the difference has changed.
The very clear message is that there is no general answer to whether it is better to set the cutoff EV above or below the vulture indifferent EV (0.8 for my game). Under one set of rules, it is better to set it below 0.8 and under another, it is better to set it above 0.8.
Again, my intuition was wrong. I was fairly sure one choice or the other would always be better.
Since drrock and I agree on the RTP calculations for my made-up game, whatever he says about the Fortune X game is probably spot on.
Quote: drrockI think that the Wizard's calculation methods were very close if not equivalent to calculating vulture optimal cutoffs.
link to original post
Yes, my cutoffs are exactly what a vulture should play.
I recognize a long-term player, trying to maximize RTP, should have slightly higher cut-offs, but that's just not how I analyze casino games.
Quote: WizardQuote: drrockI think that the Wizard's calculation methods were very close if not equivalent to calculating vulture optimal cutoffs.
link to original post
Yes, my cutoffs are exactly what a vulture should play.
I recognize a long-term player, trying to maximize RTP, should have slightly higher cut-offs, but that's just not how I analyze casino games.
link to original post
The problem is not that your cutoffs aren't optimal, it's that the player's subsequent decision to play continue playing a -EV game is non-optimal.
Quote: DRichThank you all, this has been one of the best threads on this site for quite a while.
link to original post
I agree and hate I couldn't be involved given some heavy-duty family issues. Maybe when things settle down, I'll tune in. Looks very interesting.
These questions are harder to answer because the DDB EV distribution is lumpy. I decided to do an experiment where I replaced the lumpy EV distribution with a smooth ramp function, but only for the 8X multiplier game. All other games were the DDB VP distribution. This gives a smooth axis for the X axis of the RTP vs. cutoff-EV curve. Now, if I calculate the RTP versus cutoff value, I get a smooth parabolic curve. In fact, I could generate a function for this curve and differentiate to find the optimal cutoff point. None of this is possible with a very lumpy EV distribution.Quote: drrockHmmmm....Quote: MentalI was asking whether long-term RTP changes when you move the cutoff through a neutral vulture EV (Wiz says vulture indifferent EV). If the RTP changes, is the optimum cutoff above or below this special EV? In a VP game, you will probably never find such a lucky neutral EV. That is why I invented a simple game where this is a special neutral EV value. I failed spectacularly in creating a game where there is a clear difference moving the cutoff through the vulture indifferent EV. I thought for sure there would be a clear answer one way or the other.
link to original post
I am not 100% certain, but what we have seen here thus far is that continuous-play optimal cutoffs have been more exclusive than vulture optimal cutoffs, again whether these happen to be your definition of vulture-neutral or not. By "more exclusive," I mean the multiplier acceptance probability will be lower (or, in the cases where there is no difference, at least not higher).
And I can say that is what happened in the game you invented as well, though the EVs were so, so close.
I think that the Wizard's calculation methods were very close if not equivalent to calculating vulture optimal cutoffs. I know that is what I used as initial values for cutoffs to feed into the iterative method that I used to determine what I thought should be continuous-play optimal cutoffs.
Those are the only examples that I have explored.
Other things to ponder: Is it possible to have two different consecutive hands on our spectrum that using either as a cutoff will imply the same EV? I don't know. Could slight differences in your game accomplished this? Again, I don't know. With marketable video poker games, I think it is unlikely but not 100% impossible I suppose.
Even if we figure out that games that we may define as substantially similar to Fortune X always work in a particular manner, there may be some (even minor) alteration that causes the behavior of the relationship to differ from what we see here.
link to original post
It occurred to me that I could get an almost parabola curve for the real Fortune X game if I plotted the RTP of the game versus the number of EVs in the cumulative EV distribution (instead of RTP versus EV). Effectively, this is just stretching out the x axis at all the specific EVs where the cutoff passes through the lumps of EVs.
The answer to your first question is yes, if you have discrete points on the X-axis for a parabolic curve, you can catch the maximum in such a way that the points on either side have the same RTP. It is unlikely to happen for a real-world game.
I have attached a chart of RTP versus cumulative number of EV values starting from 800 (RF) and working down. For reference, EV=1.411656 falls at 550008, but I plot this point at =(294540+546144)/2=420342, which is the center of the span of equal EVs for the high pairs, JJ,QQ,KK. It is a sad coincidence that the vulture indifferent EV falls right in this clump of EVs. Therefore, there is a dearth of data points at the peak of the parabola. The result is a reasonable approximation to an inverted parabola.
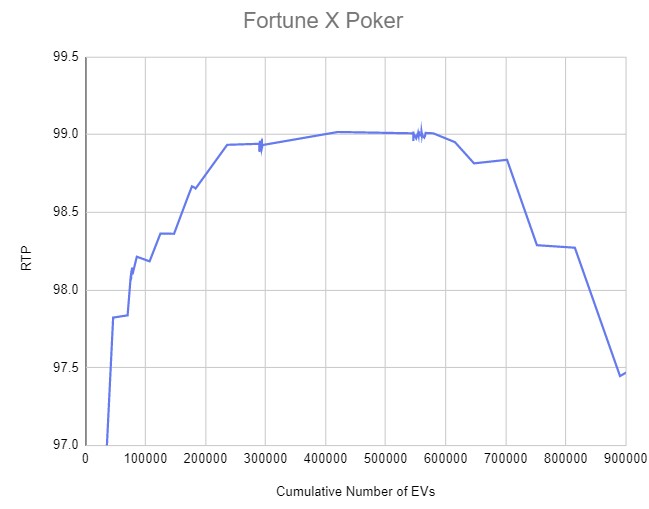
The kinks in the parabola are artifacts of the gaps in the EV. When you drop the cutoff below a clump of EVs, then a bunch of EVs switch from a 8x to a 12x multiplier and the bonus cycle changes discontinuously. In my experiment with a smooth continuous probability distribution, the parabola came out looking very smooth. The skew is due to the presence of very large EVs on the right hand side of the parabola.
Don't worry. Your normal programming of dice control, astrology, gamblers fallacy, roulette systems, and unsupported claims of gambling prowess will resume after this brief interruption.Quote: DRichThank you all, this has been one of the best threads on this site for quite a while.
link to original post
I hope I don't get banned for saying this was a really stupid comment.Quote: MentalIf you use a neutral EV cutoff point for your bonus round, you are basically saying "Let me get back to playing the base game as quickly as I can. After all, the base game has an RTP of < 50%. I want the highest possible percentage of my games to be base games, not the lucrative bonus games. Let me terminate this bonus round."
I would go in a different direction.
link to original post
I did not notice that there is one and only one multiplied hand in every bonus round and that is always the last hand in the bonus round. None of the other hands in the bonus round are multiplied. Therefore, there is no reason for the player to want to prolong the current bonus round. The player can just accept a multiplier on a good enough dealt hand and get on with waiting for the next bonus round to trigger.
Hands in the bonus round that are not multiplied are worse losers than games outside the bonus round.
Quote: MentalDon't worry. Your normal programming of dice control, astrology, gamblers fallacy, roulette systems, and unsupported claims of gambling prowess will resume after this brief interruption.Quote: DRichThank you all, this has been one of the best threads on this site for quite a while.
link to original post
link to original post
I LOL’d
I am thinking it is as simple as "optimal cutoff points are higher than indifference points between two states (or multipliers) when the indifference point has an EV above the game EV," and "optimal cutoff points are lower than indifference points when the indifference point has an EV below the game EV."Quote: MentalHands in the bonus round that are not multiplied are worse losers than games outside the bonus round.
link to original post
Other things equal, in our search for optimal EV, if we increase the frequency of states with EVs above game EV, we raise game EV, and vice versa. EV's above 1 are what makes things vulturable if that is what you are interested in, but that is not particularly germane to this post.
The indifference point could be exactly equal to the optimal cutoff, but only in the knife-edge case if the indifference point's EV was exactly equal to the game's EV (a virtually zero-probability situation without some clever mathematical manipulation).
To the statement quoted, it is true of course, but only on average and not when considering the decision around an indifference point. All the indifference points in these examples have EVs above 1 (and above the game EV); so all such hands are winners.
And, thus, also in this example, all the optimal cutoffs are higher than the indifference points.
That is an interesting conjecture about the indifference point being exactly equal to the optimal cutoff. As I mentioned, I can create a formula for derivative of the indifference expectation value (IEV) when I am substituting a continuous function for the EV probability function for the 5x game. I just haven't done it yet. I will try to find time today.Quote: drrockI am thinking it is as simple as "optimal cutoff points are higher than indifference points between two states (or multipliers) when the indifference point has an EV above the game EV," and "optimal cutoff points are lower than indifference points when the indifference point has an EV below the game EV."Quote: MentalHands in the bonus round that are not multiplied are worse losers than games outside the bonus round.
link to original post
Other things equal, in our search for optimal EV, if we increase the frequency of states with EVs above game EV, we raise game EV, and vice versa. EV's above 1 are what makes things vulturable if that is what you are interested in, but that is not particularly germane to this post.
The indifference point could be exactly equal to the optimal cutoff, but only in the knife-edge case if the indifference point's EV was exactly equal to the game's EV (a virtually zero-probability situation without some clever mathematical manipulation).
To the statement quoted, it is true of course, but only on average and not when considering the decision around an indifference point. All the indifference points in these examples have EVs above 1 (and above the game EV); so all such hands are winners.
And, thus, also in this example, all the optimal cutoffs are higher than the indifference points.
link to original post
To your last paragraph, if we are deciding whether we want a longer bonus cycle or a shorter one, then only the average return of the hands with accepted multipliers and the average return of the hands with declined multipliers matters, right?.
It would be interesting if we could find a counterexample to this conjecture. I don't think that there will be one.
Taking only the lower multiplier of the two takes us back to the lowest state of the game, the next hand after a bonus, whose EV is around 50% of the game EV; and it seems doing that one hand earlier than we have to would not be an optimal policy, thus implying that we would want such an indifference point to be lower than an optimal cutoff.
To be clear, when I say average EV of two hands, I am talking about the first of the two hands being played at 1x exactly at the indifference point and then the second hand being played with the next higher multiplier.
I found a trick that allowed me to analyze drrock's conjecture. I modified the game to use a uniform continuos probability distribution function (PDF) just for the 8x game and left the rest of the game unchanged. This allowed me to calculate the RTP analytically and to find the optimum cutoff values for various scalings of this PDF.Quote: drrockI am thinking it is as simple as "optimal cutoff points are higher than indifference points between two states (or multipliers) when the indifference point has an EV above the game EV," and "optimal cutoff points are lower than indifference points when the indifference point has an EV below the game EV."Quote: MentalHands in the bonus round that are not multiplied are worse losers than games outside the bonus round.
link to original post
Other things equal, in our search for optimal EV, if we increase the frequency of states with EVs above game EV, we raise game EV, and vice versa. EV's above 1 are what makes things vulturable if that is what you are interested in, but that is not particularly germane to this post.
The indifference point could be exactly equal to the optimal cutoff, but only in the knife-edge case if the indifference point's EV was exactly equal to the game's EV (a virtually zero-probability situation without some clever mathematical manipulation).
To the statement quoted, it is true of course, but only on average and not when considering the decision around an indifference point. All the indifference points in these examples have EVs above 1 (and above the game EV); so all such hands are winners.
And, thus, also in this example, all the optimal cutoffs are higher than the indifference points.
link to original post
For this discussion, I assume that the fraction of 2x triggers is 0.11 and the 2x, 3x, and 5x multipliers are frozen at 8.901087, 4.889740, and 2.567263.
On the average bonus sequence, there are 89/11 = 9.09 1x games and exactly one 2x multiplier game. Working through the math, I find that the average cost of getting to a 8x multiplier is C=23.46054 bets. Here I am using 5-coin bets, so the average number of games is half that, so C/2. This cost, C, is not affected by the decisions taken for the 5x game. Similarly, the yield from these games with multipliers less than 8x is Y=12.92240 bets. These numbers are treated as constants in what follows.
I calculate two other numbers, c and y, which are the combined cost and yield of the 8x and 12x games. Then, the RTP is (Y+y)/(C+c). I calculate the optimal cutoff EV for the 8x game with uniform PDF for the EV. Imagine a 'genie' shows up after an 8x game is dealt. The genie promises to produce an exact EV after the draw no matter which cards you hold. The genie picks a random number r such that 0<r<1. The genie displays an EV=rE to the player so he can make a decision. Clearly, 0<EV<E.
The 12x game, if any, is the ordinary DDB VP game with base RTP given by B=0.9898078.
I can calculate the RTP for any choice of E and cutoff EV. I introduce a convenience variable q=(cutoff EV)/E, so 0<q<1. The RTP, R, of the game can be calculated using the C++ code below.
double m = 8, M = 12, B = 0.9898078220, Y = 12.92240, C = 23.46054;
double Q = q+1.0;
double y = m*Q*(1.0-q);
y += q*q;
y *= E;
y /= 2;
y += M*B*q;
// so, y = (m*Q*(1.0-q)*E/2) + (q*q*E/2) + (M*B*q);
double c = 2*Q;
double R = (Y+y)/(C+c);
This formula is quadratic in q. I vary the value of E to change the RTP of the game. I then calculate the optimal value, O, of the cutoff EV to maximize overall RTP. I compare this to the indifference EV, I. In the table below, you can see that O=I when the RTP of the game is 100%.
q: 0.6721 E: 2.11 I: 1.4112 O: 1.4197 R: 97.054
q: 0.6405 E: 2.21 I: 1.4112 O: 1.4170 R: 97.985
q: 0.6116 E: 2.31 I: 1.4114 O: 1.4142 R: 98.969
q: 0.5851 E: 2.41 I: 1.4114 O: 1.4114 R: 100.000
q: 0.5606 E: 2.51 I: 1.4114 O: 1.4084 R: 101.072
q: 0.5379 E: 2.61 I: 1.4114 O: 1.4052 R: 102.181
q: 0.5201 E: 2.71 I: 1.4115 O: 1.4107 R: 103.323
By swapping out the lumpy EV distribution of a VP game and replacing it with a smooth PDF only for the 8x stage, I was able to turn a difficult discrete math problem into one with an analytical solution.
I'm afraid it is a bit more complicated than this in order to confirm or refute the general statement here.
I think the earlier assertion still holds:
"I am thinking it is as simple as 'optimal cutoff points are higher than indifference points between two states (or multipliers) when the indifference point has an EV above the game EV,' and 'optimal cutoff points are lower than indifference points when the indifference point has an EV below the game EV.'" [along with the later clarification: "it was the average of the two hands that needed to be above the game EV for this assertion to hold"]
"Game EV" is determined by all 6 multipliers, their frequencies, and their respective expected values for each multiplier state. Game EV relates to all hands played with all the possible multipliers, not just the two states for which an indifference point is being calculated.
In Mental's example above, game EV is based only on hands involving the 8x and 12x multipliers, leaving out the other four. That is likely why there was an equivalence found between the parameters labeled O and I.
Mental: "For this discussion, I assume that the fraction of 2x triggers is 0.11 and the 2x, 3x, and 5x multipliers are frozen at 8.901087, 4.889740, and 2.567263."
Unfortunately, in any actual game of this type, the 2x, 3x, and 5x cutoffs are dependent upon the 8x cutoff, and its resulting probability and the average payout when 8x is selected. So, when conditions change, the other cutoffs are also subject to change as well, which, until convergence, go into determining the overall Game EV. Even when the probability of the 2x trigger, which has nothing to do with a player decision, changed from 10.96% to 11%, all the cutoff values would change. I haven't previously reported on that, because my calculations, completed prior to the beginning of this thread, all involved a 2x probability of 10.96%, as shown, until at least a few days ago, on videopoker.com's help screen. Here it turned out not to affect any actual multiplier acceptance probabilities since the 11% cutoffs remained in the same "gaps" in video poker dealt hand EV distributions as the 10.96% cutoffs. However, it does clearly affect the game EV, because now there are a higher percentage of hands with non-1x multipliers. Once that 11% was accepted as the actual probability of a 2x appearing, I was able to reconcile the earlier 98.8784% EV that I calculated with YH's stated 99.01%.
This may sound circular, which is why it requires iteration, in general, to find the optimal cutoffs. When calculating cutoffs for an actual game, we get calculations for frequencies and expected values for each multiplier; but these, in turn, allow us to recalculate cutoffs. When we get the same cutoffs that we started with in an iteration, we are finished.
I can say that I am not certain if I accurately put together all the nuances in the game that Mental described. On first reading, I was anticipating that a multiplier uniformly distributed from 0 to 2 would be applied to the dealt EV, which would require a different calculation, but would have an interesting distribution that was continuous and an expected value EQUAL to the dealt hand EV. I think there would still be considerable calculation involved in the analysis if that were the case, but in this case, the probabilities of accepting the 8x multiplier would be similar to what we see in the actual Fortune X game.
With the genie and the description given,
"Imagine a 'genie' shows up after an 8x game is dealt. The genie promises to produce an exact EV after the draw no matter which cards you hold. The genie picks a random number r such that 0<r<1. The genie displays an EV=rE to the player so he can make a decision. Clearly, 0<EV<E",
it looks like the decision point perhaps is being made after the draw on an 8x hand? Although I can't tell for certain, perhaps the letter E means the dealt hand EV, and we are actually still making the decision prior to the draw on the basis of E. Either way, E seems to be about 1.0 higher than our original cutoff point, which means that 8x will be selected less often. If so, this also means that the relative frequencies of 8x and 12x will change, as well as the respective EVs when 8x and 12x are selected. If that happens, that will change the overall game EV, which will potentially change the other cutoffs, etc., etc.
At this point, it looks like all parties have come to agreement (or agreed to disagree) as to the final resolution of how to calculate the actual Fortune X's EV; e.g., it looks like the Wizard got what he wanted and published his evaluation of Fortune X. I likely don't see all the ramifications of this additional issue but who knows how all of us increasing our vast knowledge will pay benefits in the future. ;) Cheers!
Quote:An interesting mental exercise, no pun originally intended when I started this sentence.
I'm afraid it is a bit more complicated than this in order to confirm or refute the general statement here.
I believe you are a better mathematician than I pretend to be. However, you need to show some concrete example of why my conclusion is wrong. My game is 92% identical to the actual Fortune X game. I just add a genie to change the EV distribution of the flop on just the 8x hands.
Quote:I think the earlier assertion still holds:
"I am thinking it is as simple as 'optimal cutoff points are higher than indifference points between two states (or multipliers) when the indifference point has an EV above the game EV,' and 'optimal cutoff points are lower than indifference points when the indifference point has an EV below the game EV.'" [along with the later clarification: "it was the average of the two hands that needed to be above the game EV for this assertion to hold"]
I originally liked the intent of your idea. Then realized that you talk about an indifference EV close to the game EV. This has to be wrong on the face of it. The IEV is always about 1.4 in 5-bet units. I show that I and O can be equal when the game EV is zero (RTP = 100%) and the IEV is around 1.4. Maybe I am totally missing what you are claiming. What precisely are you claiming? Do you want the game RTP to be 140% before the I and O are equal?
(For clarity, I always use RTP for the total game return, and only use EV to talk about the expected value of a dealt hand relative to a 5-coin bet.)
Quote:"Game EV" is determined by all 6 multipliers, their frequencies, and their respective expected values for each multiplier state. Game EV relates to all hands played with all the possible multipliers, not just the two states for which an indifference point is being calculated.
In Mental's example above, game EV is based only on hands involving the 8x and 12x multipliers, leaving out the other four. That is likely why there was an equivalence found between the parameters labeled O and I.
I know my explanation was rather terse, but you can see that my RTP is based on the full game. All 1x hands plus the 2x, 3x, and 5x hands are wrapped up in Y and C. However these are constants within any minor variation on the real game. I don;t need to iterate. This will be true unless I do such violence to the structure of the game that the earlier 2x, 3x, and 5x decision points change enough to cross the EVs of real DDB hands. They won't, especially for 2x and 3x.
But did any of the 2x, 3x, and 5x decision points change? Which ones crossed dealt hand EVs?Quote:
Mental: "For this discussion, I assume that the fraction of 2x triggers is 0.11 and the 2x, 3x, and 5x multipliers are frozen at 8.901087, 4.889740, and 2.567263."
Unfortunately, in any actual game of this type, the 2x, 3x, and 5x cutoffs are dependent upon the 8x cutoff, and its resulting probability and the average payout when 8x is selected. So, when conditions change, the other cutoffs are also subject to change as well, which, until convergence, go into determining the overall Game EV. Even when the probability of the 2x trigger, which has nothing to do with a player decision, changed from 10.96% to 11%, all the cutoff values would change. I haven't previously reported on that, because my calculations, completed prior to the beginning of this thread, all involved a 2x probability of 10.96%, as shown, until at least a few days ago, on videopoker.com's help screen. Here it turned out not to affect any actual multiplier acceptance probabilities since the 11% cutoffs remained in the same "gaps" in video poker dealt hand EV distributions as the 10.96% cutoffs. However, it does clearly affect the game EV, because now there are a higher percentage of hands with non-1x multipliers. Once that 11% was accepted as the actual probability of a 2x appearing, I was able to reconcile the earlier 98.8784% EV that I calculated with YH's stated 99.01%.
I submit you cannot point to any decision point for lower multipliers that will change no matter how I tweak the rules of the 8x game. In particular, I am tweaking around the indifference point where the value of accepting the 5x multiplier uses a value for declining barely changes. It is probably 100% precise to view Y and C as constants unless you can find a case where they change decisions by one iota. My I and O points are essentially the one that Wiz uses. A 0.01 difference is not going to propagate back to the 5x game decision. Since the strategy and all the game rules are identical for the hands leading up to the 8x game, the yield and cost will be constant.
Quote:This may sound circular, which is why it requires iteration, in general, to find the optimal cutoffs. When calculating cutoffs for an actual game, we get calculations for frequencies and expected values for each multiplier; but these, in turn, allow us to recalculate cutoffs. When we get the same cutoffs that we started with in an iteration, we are finished.
Show me which cutoff EV move for a multiplier lower than 8x. They don't.
No, the genie tells you what your EV is after the deal. The genie rigs the draw such that that is the precise EV for the draw. If the genie says the EV of a dealt TJQKA suited is 1.4, maybe the genie will replace the Ace with a off-suit deuce often enough to make their promised EV accurate. The genie is all powerful.Quote:I can say that I am not certain if I accurately put together all the nuances in the game that Mental described. On first reading, I was anticipating that a multiplier uniformly distributed from 0 to 2 would be applied to the dealt EV, which would require a different calculation, but would have an interesting distribution that was continuous and an expected value EQUAL to the dealt hand EV. I think there would still be considerable calculation involved in the analysis if that were the case, but in this case, the probabilities of accepting the 8x multiplier would be similar to what we see in the actual Fortune X game.
With the genie and the description given,
"Imagine a 'genie' shows up after an 8x game is dealt. The genie promises to produce an exact EV after the draw no matter which cards you hold. The genie picks a random number r such that 0<r<1. The genie displays an EV=rE to the player so he can make a decision. Clearly, 0<EV<E",
it looks like the decision point perhaps is being made after the draw on an 8x hand? Although I can't tell for certain, perhaps the letter E means the dealt hand EV, and we are actually still making the decision prior to the draw on the basis of E. Either way, E seems to be about 1.0 higher than our original cutoff point, which means that 8x will be selected less often. If so, this also means that the relative frequencies of 8x and 12x will change, as well as the respective EVs when 8x and 12x are selected. If that happens, that will change the overall game EV, which will potentially change the other cutoffs, etc., etc.
I stand by the calculations that I presented. The sign flip happens when the total game EV flips from +EV to -EV. This makes intuitive sense: your decision to shorten or prolong the bonus game depends on whether it is an advantage game off the top.Quote:
At this point, it looks like all parties have come to agreement (or agreed to disagree) as to the final resolution of how to calculate the actual Fortune X's EV; e.g., it looks like the Wizard got what he wanted and published his evaluation of Fortune X. I likely don't see all the ramifications of this additional issue but who knows how all of us increasing our vast knowledge will pay benefits in the future. ;) Cheers!
Obviously, we'll need a table with EVs and probabilities for JOB hand categories such as Mental kindly provided for DDB.
Sure, I can provide the cumulative probabilities again. IIRC, folks wanted higher precision on the table so i will provide that.Quote: gordonm888Does anyone want to take a stab at the cutoffs for JOB VP? We would need to use a hit frequency for the bonus feature, I guess 11% is the obvious suspect. Alternatively, we might parameterize the JOB cutoffs as a function of feature hit frequency. I think it would be fun to see to what extent the cutoffs are different than DDB.
Obviously, we'll need a table with EVs and probabilities for JOB hand categories such as Mental kindly provided for DDB.
link to original post
My guess is that the cutoffs are largely determined by the multiplier structure and will not be much different for JOB vs. DDB.
Click this button for a list of EVs versus cumulative count for JoB.Quote: gordonm888Does anyone want to take a stab at the cutoffs for JOB VP? We would need to use a hit frequency for the bonus feature, I guess 11% is the obvious suspect. Alternatively, we might parameterize the JOB cutoffs as a function of feature hit frequency. I think it would be fun to see to what extent the cutoffs are different than DDB.
Obviously, we'll need a table with EVs and probabilities for JOB hand categories such as Mental kindly provided for DDB.
link to original post
800.00000000,4
50.00000000,40
25.00000000,664
19.68085098,760
19.65957451,796
19.59574509,820
19.55319214,848
18.55319214,944
18.53191566,992
18.48936081,1316
18.46808434,1436
18.42553139,1468
18.40425491,1504
18.36170197,1600
9.00000000,5344
6.00000000,10296
4.30249786,65208
4.00000000,75336
3.65957451,75444
3.63829780,75468
3.59574461,75588
3.57446814,75600
3.53191495,76392
2.59574461,199944
2.53191495,200052
2.51063824,200088
2.46808505,200568
2.44680858,200664
2.40425539,201720
2.38297868,201816
2.34042549,203976
1.53654027,541440
1.53284001,542280
1.52913964,542892
1.51803887,543360
1.51526368,543612
1.51433861,543828
1.51156342,544044
1.50323772,544344
1.50046253,544416
1.49953747,544644
1.49676228,544896
1.48843658,544932
1.48566139,544968
1.48288620,545556
1.48196113,545628
1.47918594,546060
1.47363555,546072
1.46993530,546084
1.46808505,546240
1.46530986,546324
1.46438479,546396
1.46160960,546468
1.45328403,546552
1.44958377,546624
1.44680846,546696
1.43663275,550008
1.43293250,551688
1.42183161,553056
1.41905642,553920
1.41813135,554424
1.41535616,554928
1.40703058,555036
1.40425527,555108
1.40333021,555132
1.40055501,555708
1.38945425,555780
1.38667905,558084
1.38297868,559260
1.37187791,559716
1.36910272,560004
1.36817765,560172
1.36540246,560340
1.35060132,560508
1.33672523,563820
1.32562447,564684
1.31914890,566412
1.30804813,566628
1.28677154,568932
1.27659571,591840
1.21276593,638928
1.14893615,655308
0.87234044,661272
0.82368177,1394412
0.80851066,1400772
0.74468082,1407420
0.73913044,1407960
0.73635525,1408176
0.73543018,1408536
0.73265493,1408716
0.72432935,1408932
0.72155410,1409184
0.72062904,1409364
0.71877891,1409400
0.71785384,1409616
0.71507865,1409652
0.70675302,1409688
0.70305270,1409724
0.68085104,1450044
0.64292324,1452096
0.64014798,1453032
0.63922292,1454292
0.63737279,1454328
0.63644773,1455264
0.63552266,1455804
0.63367254,1455876
0.63274747,1457676
0.62997222,1458576
0.62812209,1459476
0.62534690,1460160
0.62454516,1462284
0.62442183,1462788
0.62257171,1462860
0.62164664,1463616
0.62072158,1464408
0.62059820,1466016
0.61887139,1466160
0.61794633,1467672
0.61665124,1469292
0.61517113,1469580
0.61393774,1471200
0.61369103,1471836
0.61270428,1473456
0.60999078,1475724
0.60974407,1476372
0.60789394,1478532
0.60684550,1478640
0.60629046,1486104
0.60604382,1487400
0.60592043,1487508
0.60394698,1488588
0.60314524,1488696
0.60308355,1490100
0.60234350,1494612
0.60037005,1495260
0.60012335,1495476
0.60000002,1496556
0.59839654,1501092
0.59728646,1502172
0.59703976,1502388
0.59642309,1502496
0.59605306,1503576
0.59574467,1509204
0.59568304,1513740
0.59543633,1515132
0.59333950,1516428
0.59309280,1516644
0.59173602,1522692
0.58963925,1530252
0.58939254,1530684
0.58877581,1533696
0.58803576,1551660
0.58643234,1552092
0.58581561,1552308
0.58569229,1555332
0.58408880,1564272
0.58174533,1567296
0.57903177,1570320
0.57878506,1570788
0.57742828,1588908
0.57508481,1592436
0.57446808,1597356
0.57212460,1598364
0.57138455,1616508
0.56743753,1622484
0.56077707,1634580
0.55781686,1636236
0.54301572,1641168
0.54024053,1647144
0.53931546,1649088
0.53746533,1649760
0.53654027,1655376
0.53376502,1656888
0.53191489,1668192
0.52821463,1671612
0.52543938,1674528
0.52451432,1676688
0.52266419,1676712
0.52173913,1680240
0.51896393,1680576
0.51532531,1681572
0.51526362,1689612
0.51137835,1690656
0.50983655,1705296
0.50971323,1705584
0.50743139,1706652
0.50693804,1706832
0.50588959,1717740
0.50471783,1718748
0.50447118,1719264
0.50348443,1720344
0.50194263,1731300
0.50077087,1732920
0.50052422,1733448
0.49922910,1739064
0.49898243,1742976
0.49867406,1744056
0.49799567,1755036
0.49707061,1757076
0.49682394,1758156
0.49528214,1760436
0.49503547,1764372
0.49472710,1765092
0.49404871,1816368
0.49386370,1816476
0.49312365,1818060
0.49287698,1819140
0.49133518,1821420
0.49078014,1822140
0.49010175,1852560
0.48991674,1853316
0.48988310,1854108
0.48917669,1855716
0.48844784,1858236
0.48837495,1858572
0.48806661,1859292
0.48781991,1859472
0.48701259,1862352
0.48695651,1862460
0.48683318,1863180
0.48646316,1864728
0.48621646,1865256
0.48615479,1893504
0.48593614,1896120
0.48557732,1899072
0.48450089,1902024
0.48433268,1903248
0.48414207,1906200
0.48411965,1906380
0.48391780,1909692
0.48387295,1909872
0.48344126,1925688
0.48342443,1928688
0.48319456,1936560
0.48306563,1939608
0.48289743,1942452
0.48267317,1943352
0.48261711,1944480
0.48251620,1945128
0.48248255,1950624
0.48198918,1953720
0.48146218,1956924
0.48118186,1958316
0.48104730,1964220
0.48101366,1965216
0.48091274,1968336
0.48041937,1970496
0.48038572,1972368
0.48029602,1973016
0.48017269,1973196
0.48016146,1974168
0.48010540,1975584
0.48002690,1978824
0.47997084,1982952
0.47993720,1983900
0.47961202,1989900
0.47949430,1995204
0.47935414,1996200
0.47895047,1998312
0.47886077,1999284
0.47881591,2002908
0.47872621,2003988
0.47863650,2004960
0.47859165,2008200
0.47856924,2008848
0.47853559,2013336
0.47836739,2018304
0.47827768,2019348
0.47826087,2138436
0.47795251,2147244
0.47787401,2149356
0.47751522,2151516
0.47745913,2156052
0.47742552,2158212
0.47729096,2159292
0.47720125,2160360
0.47706670,2160744
0.47697699,2161824
0.47693214,2167872
0.47684243,2168304
0.47670788,2170248
0.47665182,2171664
0.47661817,2172096
0.47651726,2187120
0.47647241,2188200
0.47643876,2190360
0.47639391,2190780
0.47634906,2191104
0.47622570,2191284
0.47612479,2191932
0.47599024,2194092
0.47590053,2194740
0.47563142,2195220
0.47560900,2195328
0.47549689,2201760
0.47544080,2212200
0.47540718,2212740
0.47536233,2214900
0.47531748,2215980
0.47518292,2216520
0.47508198,2234112
0.47504836,2236152
0.47491381,2236512
0.47486895,2238648
0.47468954,2240448
0.47463349,2244648
0.47455499,2246208
0.47442043,2249136
0.47433072,2252268
0.47431391,2304576
0.47424102,2305296
0.47419617,2306808
0.47406161,2313288
0.47400555,2326632
0.47397190,2328120
0.47388220,2328660
0.47383735,2329020
0.47347856,2329380
0.47338885,2330100
0.47325429,2330820
0.47319821,2331972
0.47316459,2332692
0.47298518,2335872
0.47289547,2337924
0.47280577,2338068
0.47276092,2339688
0.47267121,2341740
0.47258151,2341884
0.47252545,2342964
0.47240210,2356284
0.47235724,2356428
0.47195357,2357148
0.47190872,2360328
0.47146019,2364108
0.47137052,2364288
0.47132567,2364648
0.47114626,2364828
0.47110140,2365308
0.47101170,2367468
0.47096685,2384076
0.47087714,2384616
0.47074258,2389584
0.47065288,2390844
0.47038376,2391348
0.47029406,2391528
0.47015950,2392536
0.47002494,2394696
0.46993524,2395704
0.46989039,2403144
0.46984553,2403324
0.46966612,2410764
0.46956521,2410944
0.46953157,2427408
0.46930733,2429856
0.46908307,2431296
0.46894851,2431836
0.46885881,2436636
0.46872425,2437716
0.46845514,2444508
0.46836543,2451204
0.46823087,2458548
0.46787205,2459088
0.46742353,2461464
0.46693018,2467080
0.46684048,2467260
0.46670592,2472552
0.46661621,2472732
0.46653771,2473020
0.46585372,2474280
0.46562946,2479320
0.46549490,2483964
0.46527064,2485692
0.46510246,2488236
0.46482214,2489856
0.46441847,2490576
0.46419421,2493744
0.46402600,2496288
0.46321869,2496672
0.46250105,2496996
0.46216467,2500776
0.46106580,2502504
0.46084154,2503368
0.45998934,2504232
0.45976508,2507400
0.45895776,2507832
0.44310823,2510856
0.42830712,2514600
0.36338472,2514612
0.36333257,2514636
0.36298314,2514648
0.36297271,2514672
0.36295706,2514696
0.36292055,2514732
0.36275366,2514756
0.36268064,2514768
0.36267543,2514828
0.36266109,2514852
0.36265457,2514876
0.36263502,2514900
0.36262849,2514912
0.36260894,2514936
0.36260241,2514960
0.36257112,2514984
0.36254504,2515020
0.36246160,2515032
0.36243552,2515056
0.36238337,2515080
0.36235732,2515116
0.36235210,2515140
0.36233646,2515164
0.36232603,2515212
0.36231038,2515224
0.36229995,2515320
0.36228952,2515332
0.36227515,2515356
0.36226344,2515380
0.36225951,2515428
0.36225823,2515440
0.36225301,2515476
0.36224908,2515524
0.36224386,2515548
0.36223215,2515584
0.36222693,2515608
0.36222300,2515632
0.36221778,2515680
0.36220735,2515704
0.36220607,2515728
0.36219692,2515752
0.36219171,2515776
0.36216563,2515896
0.36213955,2515992
0.36211348,2516040
0.36207047,2516052
0.36205611,2516076
0.36204439,2516112
0.36203396,2516148
0.36203003,2516220
0.36201832,2516292
0.36200789,2516364
0.36200395,2516412
0.36199874,2516424
0.36198309,2516448
0.36198181,2516508
0.36197788,2516532
0.36197266,2516568
0.36195701,2516592
0.36194658,2516616
0.36193487,2516640
0.36193094,2516688
0.36190879,2516724
0.36190486,2516772
0.36188272,2516856
0.36187750,2516880
0.36187357,2516928
0.36185664,2517036
0.36185142,2517072
0.36184752,2517120
0.36184230,2517144
0.36183187,2517168
0.36183056,2517216
0.36181623,2517288
0.36180580,2517360
0.36179537,2517384
0.36179015,2517456
0.36178884,2517468
0.36177972,2517528
0.36176407,2517648
0.36176276,2517672
0.36175364,2517816
0.36173800,2517912
0.36173669,2517948
0.36172757,2518044
0.36171192,2518164
0.36170149,2518224
0.36168584,2518272
0.36168063,2518284
0.36165845,2518308
0.36165455,2518500
0.36163890,2518548
0.36163238,2518596
0.36162847,2518704
0.36161283,2518824
0.36160630,2518920
0.36160240,2518980
0.36158675,2519028
0.36157632,2519136
0.36156067,2519232
0.36155936,2519256
0.36155546,2519304
0.36155024,2519376
0.36153981,2519424
0.36153460,2519520
0.36153328,2519544
0.36152938,2519592
0.36152023,2519616
0.36151373,2519688
0.36150852,2519784
0.36150721,2519832
0.36150330,2519856
0.36149809,2519868
0.36149415,2519916
0.36148766,2520012
0.36148244,2520060
0.36148113,2520132
0.36147201,2520144
0.36146808,2520240
0.36146158,2520312
0.36145636,2520336
0.36145505,2520432
0.36144593,2520456
0.36144200,2520504
0.36143550,2520600
0.36143029,2520648
0.36141986,2520672
0.36141592,2520696
0.36140943,2520744
0.36140421,2520792
0.36137813,2520936
0.36137682,2520960
0.36136249,2521008
0.36135206,2521056
0.36135074,2521128
0.36134684,2521176
0.36133641,2521272
0.36132598,2521320
0.36132467,2521404
0.36132076,2521572
0.36131033,2521716
0.36130121,2521740
0.36129990,2521764
0.36129469,2521860
0.36128426,2521908
0.36127904,2521920
0.36127773,2521932
0.36127514,2521980
0.36126861,2522004
0.36125296,2522040
0.36125165,2522052
0.36124906,2522124
0.36124253,2522196
0.36123732,2522292
0.36122689,2522364
0.36122558,2522400
0.36122167,2522424
0.36121646,2522520
0.36121124,2522928
0.36120081,2523012
0.36119950,2523036
0.36119559,2523084
0.36119038,2523132
0.36118516,2523300
0.36117995,2523348
0.36117473,2523432
0.36117342,2523480
0.36116430,2523528
0.36115909,2523768
0.36115777,2523792
0.36115387,2523840
0.36114866,2523864
0.36113822,2523888
0.36113301,2524056
0.36113170,2524104
0.36112779,2524212
0.36112258,2524236
0.36111867,2524284
0.36111736,2524356
0.36111215,2524380
0.36110824,2524452
0.36110693,2524572
0.36110562,2524620
0.36110172,2524752
0.36109650,2524908
0.36109260,2524956
0.36109129,2525028
0.36108607,2525172
0.36108217,2525292
0.36108086,2525364
0.36107954,2525496
0.36107564,2525652
0.36107042,2525760
0.36106911,2525784
0.36106652,2525856
0.36106521,2525904
0.36105999,2525976
0.36105609,2526096
0.36105478,2526144
0.36104956,2526300
0.36104435,2526396
0.36104304,2526408
0.36104044,2526456
0.36103913,2526648
0.36103392,2526720
0.36103001,2526840
0.36102349,2526936
0.36101827,2526960
0.36101437,2526984
0.36101305,2527032
0.36100784,2527056
0.36096090,2527200
0.36095700,2527320
0.36095569,2527344
0.36093482,2527392
0.36093092,2527536
0.36092961,2527560
0.36091918,2527608
0.36091527,2527632
0.36090875,2527728
0.36090484,2527896
0.36090353,2527992
0.36089310,2528112
0.36088920,2528136
0.36088267,2528184
0.36087745,2528316
0.36086702,2528412
0.36086312,2528484
0.36085790,2528508
0.36085138,2528712
0.36085007,2528748
0.36084095,2528916
0.36083704,2528964
0.36083573,2529108
0.36083183,2529180
0.36082530,2529396
0.36082399,2529432
0.36082008,2529456
0.36081618,2529504
0.36081487,2529648
0.36081097,2529720
0.36080965,2529888
0.36080575,2530008
0.36080053,2530032
0.36079922,2530188
0.36079791,2530236
0.36079401,2530380
0.36079010,2530476
0.36078879,2530572
0.36078358,2530716
0.36077967,2530812
0.36077315,2530860
0.36076793,2530956
0.36076403,2530980
0.36076272,2531028
0.36075750,2531100
0.36075360,2531148
0.36075228,2531196
0.36074838,2531244
0.36074185,2531364
0.36073795,2531436
0.36073664,2531484
0.36073273,2531508
0.36072621,2531556
0.36072230,2531628
0.36071578,2531796
0.36071056,2531844
0.36070666,2531892
0.36070013,2531976
0.36068970,2532168
0.36068448,2532312
0.36068058,2532408
0.36067405,2532552
0.36066362,2532696
0.36065841,2532744
0.36065450,2532768
0.36065319,2532936
0.36064798,2533020
0.36063886,2533044
0.36063755,2533236
0.36063233,2533284
0.36062843,2533332
0.36062711,2533452
0.36062190,2533572
0.36061278,2533644
0.36060625,2533668
0.36060104,2533812
0.36059713,2533860
0.36059582,2533968
0.36058670,2534040
0.36058149,2534112
0.36057496,2534172
0.36057106,2534244
0.36056975,2534424
0.36056843,2534448
0.36056584,2534472
0.36056063,2534568
0.36055541,2534664
0.36054888,2534736
0.36054498,2534760
0.36054367,2535060
0.36054236,2535084
0.36053976,2535156
0.36053455,2535204
0.36052933,2535396
0.36052802,2535420
0.36052281,2535480
0.36051890,2535576
0.36051759,2535816
0.36051628,2535840
0.36051369,2535960
0.36050847,2536008
0.36050326,2536224
0.36050195,2536368
0.36049804,2536392
0.36049673,2536452
0.36049151,2536644
0.36048761,2536716
0.36047587,2536812
0.36047196,2536836
0.36047065,2536848
0.36046544,2537040
0.36046153,2537280
0.36045632,2537400
0.36044979,2537448
0.36044589,2537496
0.36044458,2537520
0.36044067,2537544
0.36043936,2537712
0.36043546,2537952
0.36043414,2538168
0.36043024,2538456
0.36042503,2538504
0.36042371,2538540
0.36041981,2538564
0.36041850,2538588
0.36041459,2538612
0.36041328,2538708
0.36040938,2538900
0.36040807,2539116
0.36040416,2539524
0.36039895,2539596
0.36039373,2539716
0.36039242,2539884
0.36038852,2539980
0.36038721,2540028
0.36038330,2540268
0.36038199,2540340
0.36037809,2540772
0.36037678,2540808
0.36037287,2540928
0.36036634,2541024
0.36036244,2541072
0.36036113,2541120
0.36035722,2541144
0.36035070,2541192
0.36034679,2541240
0.36034027,2541432
0.36033636,2541480
0.36032462,2541612
0.36032072,2541708
0.36031941,2541780
0.36031419,2541972
0.36030507,2542092
0.36029854,2542260
0.36028811,2542452
0.36027899,2542524
0.36027768,2542536
0.36027247,2542692
0.36026204,2542836
0.36025292,2542932
0.36025161,2542980
0.36023596,2543148
0.36022684,2543196
0.36022553,2543244
0.36022162,2543268
0.36020988,2543412
0.36020598,2543508
0.36019945,2543568
0.36019555,2543664
0.36018381,2543832
0.36017990,2543976
0.36017337,2544132
0.36016947,2544252
0.36016816,2544324
0.36016035,2544372
0.36015773,2544684
0.36015382,2544972
0.36014730,2545128
0.36014339,2545224
0.36014208,2545272
0.36013818,2545344
0.36013687,2545368
0.36013427,2545440
0.36013165,2545608
0.36012775,2545680
0.36012644,2545776
0.36012122,2545884
0.36011732,2546028
0.36011210,2546100
0.36011079,2546124
0.36010820,2546172
0.36010557,2546316
0.36010167,2546556
0.36010036,2546700
0.36009645,2546796
0.36009514,2546808
0.36008602,2547048
0.36008471,2547120
0.36008212,2547192
0.36007950,2547264
0.36007038,2547336
0.36006907,2547348
0.36005995,2547564
0.36005864,2547684
0.36005473,2547732
0.36004430,2547900
0.36004299,2547960
0.36003909,2548032
0.36003387,2548176
0.36003256,2548344
0.36002865,2548680
0.36001822,2548752
0.36001691,2548920
0.36001301,2549112
0.36000779,2549232
0.36000648,2549352
0.36000258,2549544
0.35999215,2549856
0.35999084,2550000
0.35998693,2550288
0.35998172,2550504
0.35998040,2550624
0.35997650,2550816
0.35996476,2550888
0.35996085,2551152
0.35995564,2551176
0.35995433,2551248
0.35994911,2551296
0.35994130,2551320
0.35993868,2551488
0.35993478,2551824
0.35992956,2551992
0.35992825,2552040
0.35992303,2552088
0.35991523,2552184
0.35991260,2552376
0.35990870,2552808
0.35990348,2553120
0.35990217,2553144
0.35989827,2553240
0.35989696,2553312
0.35988915,2553336
0.35988653,2553552
0.35988262,2553888
0.35987741,2554056
0.35987610,2554212
0.35987219,2554404
0.35986307,2554500
0.35986045,2554632
0.35985655,2555112
0.35985133,2555376
0.35985002,2555436
0.35984612,2555748
0.35984221,2555772
0.35983437,2555844
0.35982525,2555892
0.35982394,2556012
0.35982004,2556372
0.35981873,2556516
0.35981613,2556588
0.35979787,2556660
0.35979396,2556876
0.35979006,2556972
0.35977831,2557068
0.35977182,2557140
0.35976788,2557284
0.35976398,2557308
0.35974702,2557332
0.35974574,2557404
0.35974181,2557452
0.35973790,2557716
0.35973659,2557764
0.35973531,2557788
0.35972095,2557812
0.35971573,2557956
0.35971051,2558004
0.35970923,2558100
0.35970008,2558172
0.35969487,2558340
0.35968444,2558532
0.35968316,2558604
0.35966879,2558724
0.35966751,2558796
0.35965967,2558820
0.35965836,2559012
0.35965708,2559108
0.35965315,2559372
0.35964271,2559540
0.35964143,2559612
0.35963750,2559636
0.35963359,2559660
0.35963228,2559780
0.35963100,2559924
0.35962707,2560308
0.35961664,2560428
0.35961536,2560524
0.35961142,2560620
0.35960752,2560692
0.35960621,2560740
0.35960492,2560884
0.35960099,2561196
0.35959056,2561436
0.35958534,2561628
0.35958144,2561676
0.35958013,2561748
0.35957885,2561844
0.35957491,2561964
0.35955927,2562204
0.35955536,2562276
0.35955277,2562324
0.35953841,2562348
0.35953319,2562588
0.35952798,2562828
0.35951233,2562948
0.35950711,2563164
0.35950190,2563620
0.35948625,2563956
0.35948104,2564172
0.35947582,2564556
0.35947061,2564652
0.35946018,2564844
0.35945496,2565132
0.35944974,2565228
0.35944846,2565276
0.35944062,2565348
0.35943410,2565588
0.35942888,2565636
0.35942760,2565732
0.35942239,2565780
0.35941845,2565924
0.35941455,2565996
0.35940802,2566284
0.35940281,2566596
0.35940152,2566692
0.35939631,2566740
0.35938847,2566908
0.35938716,2567004
0.35938588,2567028
0.35938194,2567244
0.35937673,2567580
0.35937545,2567628
0.35937023,2567736
0.35936239,2567832
0.35936108,2567904
0.35935980,2567928
0.35935587,2568096
0.35935065,2568408
0.35934937,2568504
0.35934544,2568528
0.35933632,2568840
0.35933501,2569008
0.35933372,2569032
0.35932979,2569272
0.35932457,2569464
0.35932329,2569656
0.35931936,2569800
0.35931545,2569896
0.35930893,2569968
0.35929850,2570136
0.35929722,2570232
0.35929328,2570448
0.35928938,2570616
0.35928285,2570904
0.35927764,2570928
0.35927114,2571024
0.35926720,2571192
0.35926330,2571528
0.35925809,2571576
0.35925680,2571648
0.35925159,2571984
0.35924116,2572080
0.35923722,2572248
0.35923594,2572320
0.35923201,2572344
0.35922551,2572392
0.35921508,2572512
0.35921115,2573184
0.35920987,2573448
0.35920593,2573496
0.35920465,2573592
0.35919943,2573808
0.35918900,2574024
0.35918379,2574216
0.35917985,2574264
0.35917857,2574360
0.35917336,2574408
0.35915771,2574840
0.35915378,2574912
0.35915250,2574960
0.35913685,2575080
0.35913163,2575488
0.35912642,2575704
0.35911077,2575896
0.35910556,2576232
0.35910034,2576472
0.35908470,2576616
0.35907948,2576856
0.35907426,2577000
0.35905862,2577144
0.35905340,2577408
0.35903904,2577456
0.35903254,2577744
0.35902733,2577792
0.35901296,2577840
0.35900646,2578200
0.35900125,2578344
0.35898688,2578512
0.35898560,2578608
0.35898039,2578920
0.35897517,2579208
0.35896081,2579256
0.35895953,2579376
0.35895431,2579712
0.35894910,2579760
0.35894388,2579952
0.35893473,2580120
0.35893345,2580216
0.35892823,2580600
0.35892302,2580696
0.35891780,2580984
0.35891387,2581080
0.35890737,2581152
0.35890216,2581224
0.35889694,2581272
0.35888779,2581416
0.35888129,2581512
0.35887608,2581632
0.35886171,2581824
0.35885000,2581992
0.35883564,2582136
0.35883436,2582184
0.35882393,2582304
0.35880956,2582688
0.35880828,2582784
0.35879785,2582904
0.35878870,2583000
0.35878220,2583048
0.35877177,2583120
0.35876262,2583168
0.35875612,2583360
0.35874569,2583408
0.35873657,2583576
0.35873526,2583600
0.35873136,2583744
0.35873005,2583888
0.35872483,2584176
0.35871962,2584200
0.35871050,2584272
0.35870919,2584392
0.35870528,2584608
0.35870397,2584704
0.35869876,2584920
0.35869354,2585064
0.35868442,2585400
0.35868311,2585496
0.35867921,2585664
0.35867789,2585856
0.35866746,2585904
0.35865703,2585976
0.35865313,2586144
0.35865182,2586288
0.35864139,2586360
0.35863748,2586408
0.35863617,2586552
0.35863096,2586720
0.35862705,2586984
0.35862574,2587080
0.35861531,2587104
0.35861140,2587128
0.35860619,2587176
0.35860488,2587344
0.35859966,2587440
0.35858533,2587488
0.35858011,2587512
0.35857880,2587704
0.35857359,2587752
0.35855925,2587800
0.35855404,2587848
0.35855272,2588040
0.35853317,2588112
0.35852796,2588160
0.35852665,2588448
0.35851231,2588592
0.35850188,2588664
0.35850057,2588808
0.35848624,2589144
0.35847449,2589336
0.35846016,2589600
0.35844842,2589888
0.35843408,2590080
0.35842234,2590368
0.35840800,2590872
0.35839626,2591064
0.35838714,2591280
0.35837018,2591376
0.35836107,2591616
0.35833499,2591808
0.35833368,2591928
0.35832977,2592024
0.35830891,2592216
0.35830760,2592312
0.35830370,2592408
0.35828283,2593008
0.35828152,2593104
0.35827762,2593200
0.35825545,2593248
0.35825154,2593344
0.35824502,2593440
0.35822937,2593584
0.35822546,2593680
0.35821894,2593776
0.35820460,2593872
0.35820329,2594064
0.35819286,2594112
0.35817853,2594184
0.35817721,2594376
0.35816678,2594472
0.35815245,2594592
0.35815114,2594712
0.35814071,2594904
0.35812637,2594976
0.35812506,2595048
0.35811463,2595144
0.35811073,2595192
0.35810030,2595312
0.35808855,2595408
0.35808465,2595552
0.35805857,2595648
0.35803249,2595696
0.35802206,2595744
0.35800642,2595888
0.35799599,2595960
0.35798556,2596080
0.35796991,2596128
0.35795948,2596272
0.35794383,2596320
0.35793340,2596416
0.35791776,2596440
0.35790733,2596560
0.35788125,2596800
0.35780302,2596992
0.35777694,2597232
0.35775086,2597424
0.35772479,2597568
0.35769871,2597760
0.35758397,2597952
0.35755789,2598048
0.35753182,2598144
0.35750574,2598264
0.35749531,2598408
0.35747966,2598624
0.35746923,2598720
0.35744315,2598816
0.35741708,2598912
0.35739100,2598960
I am guessing that the trigger ratio = 0.116 to make the RTP come out right.
Beyond that, here is what I have for you:
(1) Even if all the lower cutoffs would remain the same (and they don't*), there are still a couple other issues. In your genie game the transition probability from 8x to 12x is different than in the Fortune X game. I’m not sure, but guessing that perhaps your q is that probability?
You may recall that in the 3rd page of this thread, I outlined a number of equations that led to the calculation of the frequencies of the different multipliers. One of those equations was "p12 = 0.7883783 p8". The coefficient was the percentage of the time that the 8x multiplier was not accepted or the percentage of the time that the 12x multiplier occurred on the hand after the 8x multiplier. This is just one of 6 (or 7) equations in a system of equations to be solved.
Once that coefficient changes, even if none of the other transition probabilities (or coefficients) change, the answer for all the p's in that system of equations changes. The game EV is p1 x EV1 + p2 x EV2 + p3 x EV3 + p5 x EV5 + p8 x EV8 + p12 x EV12; so if even one p changes, the game EV changes, other things equal. And you can’t really have only one p changing, since they must add to 1. I did not see what your estimates were for each of the 12 items above in your example. I know you say they are all combined in one figure, but unless you break them out into those 12 items, I don’t think I can find precisely where we differ. But please see if any of what follows helps.
When your genie game gets an EV of 100% by changing EV8. p1, p2, p3, and p5 will also change, which is why I was suggesting iteration even if EV2, EV3, and EV5 do not change. We don't have to worry about EV1 or EV12 because they will not change, but p1 and p12 will change.
(2) In your table, you have the indifference point changing slightly varying from 1.4112 to 1.4115. Since the 12x EV never changes, and is the same in your example as in the Fortune X game, I don't think the indifference point between 8x and 12x ever changes; so it should remain at the Wizard's value of 1.41109914. He showed that calculation earlier in the thread with some simple algebra. I don’t know which equations allowed you to get your numbers nor why the indifference point would vary.
And since the indifference point is somewhat variable in your examples, it is hard to confirm a particularly flipping point.
(3) Re: this quote,
Mental: "Then realized that you talk about an indifference EV close to the game EV. This has to be wrong on the face of it."
I think I like the term indifference point better than indifference EV. I'm not certain where I talk about indifference points being close to game EV, but maybe we have been too loose with our terms, or maybe I made a typo (or inadvertent “logico” somewhere). I think somewhere I said something like, "In all these examples, the optimal cutoff is higher than the indifference points." I theorized that this was because all the indifference points were above the game EV (perhaps I should have clarified "with the indifference point being the multiplied value at the lower multiplier under consideration,” since we have all been using indifference points and EVs that have only 5 coins in the denominator rather than 10). While something around 1.4 is what we are using for 8x, it would be closer to 0.7 if we were calculating EV as a 10-coin game.
I think I did say that the optimal cutoffs were near the indifference points. However, I don't recall indicating that the indifference points were particularly near the game EV; but if I did that would be incorrect. It doesn't happen with this game or either of your examples. It could happen in some other game, I suppose.
(4) *As it turns out, I believe, at least on the first iteration of your genie game, that the change to increasing the game EV to 100% causes the 2x cutoff to exceed 45 coins (or 9.00 five-coin bets), thus changing the action necessary for dealt full houses and the probability of transition from 2x to 3x. With a dealt full house and the first pass thru with the 100% EV, we would forego the 2x multiplier and hope for a higher payout on a future hand with a larger multiplier. Again this is the cutoff, not the indifference point. This is just unlucky for your example, but of course could happen at any time. And even if a cutoff change didn’t happen on a particular iteration, changes in probabilities are more likely with any change and need to be accounted for. When the Wizard found out from YH that the percentage for 2x changed a tiny bit from 10.96% to 11.00%, the game EV went from 98.88% to 99.01%.
I don't know if this convinces you. It is always tempting to ask someone else to point out exactly where an example fails. I think I have pointed a couple items out, but this thread is probably not the best medium to get everything resolved.
It is difficult with these games to get something to work out to an exact game EV because of the interdependencies. As you point out, it is a little easier because of the gaps in the distributions, but you need to be able to hold the transition probabilities constant if you are going to try to get a certain exact percentage EV by changing some of the EVs for an individual multiplier or two.
(5) Just as I was getting ready to post this, I thought of one more bit of logic. Look at your concluding paragraph:
"I stand by the calculations that I presented. The sign flip happens when the total game EV flips from +EV to -EV. This makes intuitive sense: your decision to shorten or prolong the bonus game depends on whether it is an advantage game off the top."
The claim in your example is that the indifference point is identical to the optimal cutoff between 8x and 12x and that this make sense because the game EV is 100%. Above I have pointed out a couple reasons why your example’s EV is not 100%. But here is another question: If the game EV being 100% is what would cause an optimal cutoff to equal an indifference point, why is it that only the 8x-12x cutoff in your example has this relationship? The optimal cutoffs for 2x, 3x, and 5x remain above the indifference points in your example. Do you account for the other cutoffs still being higher and not equal to the indifference points simply due to continuity? Calculating an indifference point has never had anything to do with continuity.
(6) If you need any more convincing, please try to calculate separately the 12 components of game EV above. I might be able to see how these compare, and if they balance out with what we think the transition probabilities are going from multiplier to multiplier.
Gordon, I'll take a look, but will be happy if someone beats me to it. As you can tell, I just took a long time on the previous post.
I am fairly drunk right now, but I want to send a quick note to say that I am always impressed at how thoroughly you understand the moving parts of this problem. You also perceived most of the gist of my game modification even though I didn't want to spend the time going through it in detail. I have some differences with you over one point, but your perspective has been very helpful to me.Quote: drrockMental, I don’t claim to be a better mathematician. You’re demonstrating lots of tricks and techniques yourself. But who is better sometimes won’t get us to a better answer. And we can all make mistakes. These always end up being longer than I would like. If you don't have a lot of time now, reread your concluding paragraph and look at (5) below. See if this raises at least a doubt as to your conclusion.
link to original post
The the indifference point between 8x and 12x changes because I am changing the shape of the EV distribution for the 5x game. This is how I tweak the overall RTP. The EV distribution static in the game the Wiz analyzes. I could still be wrong, but this is not a proof.
More tomorrow.
Cheers.
Quote: gordonm888Does anyone want to take a stab at the cutoffs for JOB VP? We would need to use a hit frequency for the bonus feature, I guess 11% is the obvious suspect. Alternatively, we might parameterize the JOB cutoffs as a function of feature hit frequency. I think it would be fun to see to what extent the cutoffs are different than DDB.
Obviously, we'll need a table with EVs and probabilities for JOB hand categories such as Mental kindly provided for DDB.
link to original post
| Mult | Wizard* | DrRock | Difference | LoHandEV | HiHandEV | InBetween |
|---|---|---|---|---|---|---|
| 2x | 8.514869 | 8.646949 | 0.132080 | 6.000000 | 9.000000 | 0 |
| 3x | 4.739431 | 4.781851 | 0.042420 | 4.302498 | 6.000000 | 0 |
| 5x | 2.546356 | 2.557272 | 0.010916 | 2.531915 | 2.595745 | 0 |
| 8x | 1.420753 | 1.421622 | 0.000869 | 1.419056 | 1.421832 | 0 |
LoHandEV shows the EV of the hands that have the highest EV that are still below the Wizard's cutoff. HiHandEV shows the EV of the hands that have the lowest EV that are still above my cutoff. This time there is no difference depending upon which cutoffs are used. Each pair of cutoffs reside in the same gap. (Reminder: InBetween shows the number of dealt hands out of 2,598,960 that would be counted differently depending upon which set of cutoffs is used. And this time that number is always zero.)
*Obviously, the Wizard did NOT calculate these. I was able to duplicate the calculations that he made for DDB, and I believe that I did them in the same manner here for 9/6 Jacks or Better.
Something troublesome, which could indicate that I missed something unless this can be verified by the Wizard or YH, is that I calculated an EV of only 97.6130%. I did use the 11% frequency for 2x bonus appearing. Maybe this is wrong or I have an error somewhere in my spreadsheet.
I say this is troubling because we saw that the 98.98% base game for DDB became 99.01% under Fortune X. And I understand a lot of games with novel features like multipliers have an EV that is designed to be equal to or just a touch above that of the base game. Clearly 97.61% is pretty underwhelming for a 99.54% base game.
Great stuff!Quote: drrockI say this is troubling because we saw that the 98.98% base game for DDB became 99.01% under Fortune X. And I understand a lot of games with novel features like multipliers have an EV that is designed to be equal to or just a touch above that of the base game. Clearly 97.61% is pretty underwhelming for a 99.54% base game.
link to original post
My MC sims agree with your result. That is why I boosted the trigger ratio (trigger = 0.116;) in my sims. It brings my RTP up to the 99.5% range which is probably how the game is designed. I wish we had all the actual trigger probabilities.
I did not integrate the PDF to get cutoffs. I just iterated the MC sims to estimate the 8x cutoff, then the 5x cutoff, etc. Your direct method is faster. Note that the real game requires numerical integration over a discrete cumulative PDF. My modified game just substituted a uniform PDF for the 8x stage so the cPDF was a line that I could integrate analytically. I should just do the direct numerical integration like you do. The MC sims sample the cPDF and act like an integrator.
We are using different (but mathematically equivalent) approaches.Quote: drrockOnce that coefficient changes, even if none of the other transition probabilities (or coefficients) change, the answer for all the p's in that system of equations changes. The game EV is p1 x EV1 + p2 x EV2 + p3 x EV3 + p5 x EV5 + p8 x EV8 + p12 x EV12; so if even one p changes, the game EV changes, other things equal. And you can’t really have only one p changing, since they must add to 1. I did not see what your estimates were for each of the 12 items above in your example. I know you say they are all combined in one figure, but unless you break them out into those 12 items, I don’t think I can find precisely where we differ. But please see if any of what follows helps.
When your genie game gets an EV of 100% by changing EV8. p1, p2, p3, and p5 will also change, which is why I was suggesting iteration even if EV2, EV3, and EV5 do not change. We don't have to worry about EV1 or EV12 because they will not change, but p1 and p12 will change.
link to original post
Your p1,p2,.. are the fractions of times the games are in the 1x,2x,3x,5x.8x,12x states. In my approach, I am using V[x] which is the absolute number of times in an average bonus cycle that we visit a game where the [x] multiplier is offered. I consider normal base games to be 1x. Then V[2] = 1. It is a constant. You will always see one and only one 2x multiplier offered in every cycle. To make the math simple, if the bonus trigger rate was a simple fraction like 1/10, then V[1] = 9, also constant. The first variable is V[3]. It is V[2] times the rejection ratio for the 2x multiplier (or 1 - acceptance ratio).
My average bonus cycle length, L, is the sum V[1]+V[2]+V[3]+V[5]+V[8]+V[12] = L. So, L varies based on the multiplier acceptance strategy, that is, the cutoffs values that are used. Your p1 = V[1] / L. right? For you, p1 is a variable based on strategy. For me, V[1] is a constant independent of strategy, and L is the varying quantity to be determined. Both approaches are equivalent.
After rereading your long post, I don't see any significant areas of disagreement that aren't likely us just using different terminology. You are right that we could be sure about our level of agreement if I will create a table with all of my transition probabilities at each stage. I prefer to work with V[x], but I can calculate V[x] and pn so you can easily compare my results with yours.Quote: drrock(6) If you need any more convincing, please try to calculate separately the 12 components of game EV above. I might be able to see how these compare, and if they balance out with what we think the transition probabilities are going from multiplier to multiplier.
link to original post
I am going to see if I am near any accidental jumps across dealt hand EVs in my modified game. This is mathematically impossible at any one value of my scaling factor, E, but it could happen as I change E to change the overall RTP.
Quote: drrockQuote: gordonm888Does anyone want to take a stab at the cutoffs for JOB VP? We would need to use a hit frequency for the bonus feature, I guess 11% is the obvious suspect. Alternatively, we might parameterize the JOB cutoffs as a function of feature hit frequency. I think it would be fun to see to what extent the cutoffs are different than DDB.
Obviously, we'll need a table with EVs and probabilities for JOB hand categories such as Mental kindly provided for DDB.
link to original post
Mult Wizard* DrRock Difference LoHandEV HiHandEV InBetween 2x 8.514869 8.646949 0.132080 6.000000 9.000000 0 3x 4.739431 4.781851 0.042420 4.302498 6.000000 0 5x 2.546356 2.557272 0.010916 2.531915 2.595745 0 8x 1.420753 1.421622 0.000869 1.419056 1.421832 0
LoHandEV shows the EV of the hands that have the highest EV that are still below the Wizard's cutoff. HiHandEV shows the EV of the hands that have the lowest EV that are still above my cutoff. This time there is no difference depending upon which cutoffs are used. Each pair of cutoffs reside in the same gap. (Reminder: InBetween shows the number of dealt hands out of 2,598,960 that would be counted differently depending upon which set of cutoffs is used. And this time that number is always zero.)
*Obviously, the Wizard did NOT calculate these. I was able to duplicate the calculations that he made for DDB, and I believe that I did them in the same manner here for 9/6 Jacks or Better.
Something troublesome, which could indicate that I missed something unless this can be verified by the Wizard or YH, is that I calculated an EV of only 97.6130%. I did use the 11% frequency for 2x bonus appearing. Maybe this is wrong or I have an error somewhere in my spreadsheet.
I say this is troubling because we saw that the 98.98% base game for DDB became 99.01% under Fortune X. And I understand a lot of games with novel features like multipliers have an EV that is designed to be equal to or just a touch above that of the base game. Clearly 97.61% is pretty underwhelming for a 99.54% base game.
link to original post
I understand the trigger percentage for this game is 11.65%. The cutoffs change, but do not move out of the gaps. The leverage of this 0.65% change in trigger point is pretty big, moving the game EV to 99.5995%. While two examples may not assure a pattern, it looks like the trigger percentages for the two games (Jacks or Better and DDB) are chosen to nudge Fortune X's EVs just over the base game EVs.
There are 11 different trigger points listed for the 13 game types. In general, it looks like the games with the higher variances have lower trigger points and vice versa. This would be expected due to the advantage of being able to choose which hands get a multiplier when there is a higher probability of more extreme winning dealt hands.
None of the games have the originally published trigger point of 10.96%. The average of the 13 games is 10.93%. If the duplicated percentages are eliminated, the average of the 11 unique values is 10.97%. If someone truncated rather than rounded the latter percentage (10.9655%), that would have yielded 10.96% as an average. Or perhaps there are some more Fortune X games available than the 13 they have room to present on the website. Or the currently published percentages are just accurate to two places.
Thanks for the update on trigger frequencies.Quote: drrockI can also report that the trigger percentages for these games have been updated today at videopoker.com.
There are 11 different trigger points listed for the 13 game types. In general, it looks like the games with the higher variances have lower trigger points and vice versa. This would be expected due to the advantage of being able to choose which hands get a multiplier when there is a higher probability of more extreme winning dealt hands.link to original post
I have busy losing a boatload of money online today. However, I have some time to write some code now. I should be able to automate the search for cutoff values. I also figure you might want the weighted EVs for all deals above any given cutoff point. Some nomenclature: If I give a cutoff point as 50.0 or 40, I mean that dealt RFs and SFs are all accepted for multiplication. Here are the first 15 lines in my new output (printed here without commas). Are these the weighted EVs you need for your calculations or something else? You might also want the weighted EVs for all deals below the cutoff, but I think that can be derived from these numbers.
800.00000000 4 800.00000000
50.00000000 40 125.00000000
25.00000000 664 31.02409639
19.68085098 760 29.59126539
19.65957451 796 29.14209344
19.59574509 820 28.86268812
19.55319214 848 28.55529910
18.55319214 944 27.53813568
18.53191566 992 27.10235084
18.48936081 1316 24.98182746
18.46808434 1436 24.43750352
18.42553139 1468 24.30645236
18.40425491 1504 24.16517636
18.36170197 1600 23.81696789
9.00000000 5344 13.43621793
Personally, I would rather not have to deal with any weighting for any hands, no matter how obvious it might seem that we would select certain dealt hands for multiplication. It takes me less time to deal with the unweighted information since I have already put together worksheets to handle the separations and weighting.
Bottom line: I prefer what you have already done for Jacks or Better to anything else.
I also prefer the complete enumeration rather than any cutoff. That way I can check the total EV of the base game to see if it matches with other calculations to assure that I'm not doing something wrong. I have a few checks already built into Excel spreadsheets for that.
The worksheet that I use accepts tentative cutoffs and immediately improves on them if necessary, or tells me that I'm finished. If the next-step cutoffs are different than what I started with, it is as easy as highlighting the 4 cells containing the 2x, 3x, 5x, and 8x cutoffs and then Copy Paste Values into my 4 starting value cells and rechecking. It has never taken more than 3 and possibly only 2 iterations, which take only a couple seconds of time. It actually is more work to look for indifference points than doing any of the rest of the work at this point, not that it is that difficult.
The Wizard's statement on his Fortune X page, "For games other than 9-6 Double Double Bonus, the breakeven points should still be about the same, but not exactly" is accurate. So for most people, and "government work," it is probably just fine to use the numbers he has on his page for playing all the games. That is not the way that I do it, but as you might have gathered, I'm rather fussy about getting the best precision possible.
With the two games we have worked on in this column, my way only improves game EV by 0.0001% for 9-6 DDB and not at all for 9-6 Jacks or Better. So if it is easier for some to use breakeven values, they are not going to suffer financially one bit.
One advantage of NOT using breakeven values: The way I calculate Fortune X, you can actually use another game's ending values as starting values for iteration instead of looking for breakeven points.


