How Can We Know?

In a recent thread, Shack posted that if you use FPDW strategy on the 12-4-3 Double Bonus Deuces Wild game, you give up 1.77%, and that you should never play a bonus game with a flat deuces strategy.

I certainly agree with the conclusion. Bonus deuces games return 1-1 for straights and you never hold 4-card straights. In regular deuces games, straights pay 2-1 and you go for 4-card straights and 4-card inside straights regularly. And personally, even giving up 0.01% by using 9/6 JoB strategy to play 8/5 BP is WAY too much for me to voluntarily give up.

Still, the discussion left me wondering.

The part of this I have trouble understanding is the 1.77% difference --- with no backstory --- insofar as it applies to play hands involving two pair. In FPDW, if you’re dealt two pair, you hold one and toss one. Doesn’t matter which one.

In DBDW, if you’re dealt two pair, you hold one and toss one, and it often DOES matter which one. Because of the differing sizes of payouts on 5-of-a-kinds, you prefer holding AA to {33, 44, 55} which in turn you prefer over {66, 77, . . ., QQ, KK}.

Back to FPDW. While it doesn’t matter which pair you hold from two pair, every computer program playing the game has to have a method of picking one. Whatever method the computer uses to pick one pair is equivalent to any other method. So long as you’re playing FPDW.

When you’re using that program to play another game where it DOES matter which pair you pick, now the original methodology for picking pairs matters a lot. If your program picked the first pair from the left, so that from 44AAK it picks fours but from AA44K it picks aces, that works fine for FPDW but not so fine for DBDW.

But we aren’t told what methodology the program uses. We just are told that there’s a 1.77% difference. That’s a lot of precision when we don’t even know if the program always holds aces from 44AAK. How can we know? Some of us have inquiring minds.

BTW, I will be online very sporadically for the next two weeks. It's very possible this thread will be dead and buried by the time I get back in early July, but if there's something interesting in it, I'll resurrect it at that time.

Interesting. I would assume playing FPDW we would be holding the "correct" pair (of two pair) for DBDW half of the time. I also wonder if that is factored into the 1.77% difference.

On another note, when the pair to hold doesn't matter how do people decide which pair to hold? I usually hold the leftmost pair because it tends to be less arm movement for me.

Thank you for posting and adding content to this forum. You are a gentleman and a scholar

Quote: DRich

On another note, when the pair to hold doesn't matter how do people decide which pair to hold?

Whichever card has been hotter is the one I hold, because that is the one most likely to come up on the draw

Very good point! To address your concern, I could dust off my own video poker program to make sure it chooses a pair of aces first, and 3's to 5's second, when indifferent in choosing one of two pairs. However, I can also trick JB's video poker analyzer to do it.

What I did was first put in the standard pays for Full Pay Deuces Wild. Then I multiplied all of them by 1,000, which would leave the strategy the same. Then I added 2 to the pay of fives and and 1 to the pay of five 3's to 5's. In other words, pays of 15,002 for five aces, 15,001 for five 3's to 5's, and 15,000 for five 6's to Ks. I figured that the extra coin or two wouldn't affect the strategy, except to force the game to choose the pairs the way I wanted.

Here is what I put into it:



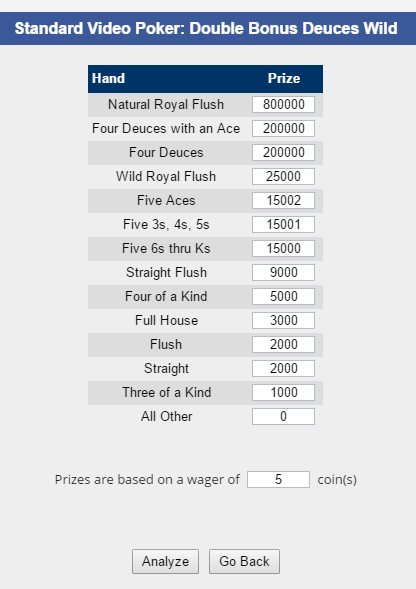
And the results:



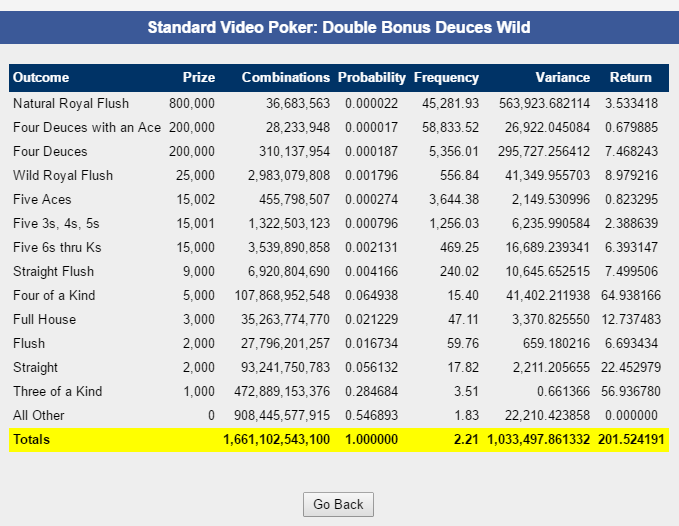
The following table shows the combinations of each hand under the original combinations, which my previous post was based on, and the modified combinations. Both result in exactly the same return for the Full Pay pay table.

HAND	Original combinations	Gaffed Combinations	Difference
Natural royal flush	36,683,563	36,683,563	-
Four deuces + A	28,233,948	28,233,948	-
Four deuces + 3-K	310,137,954	310,137,954	-
Wild royal flush	2,983,079,808	2,983,079,808	-
Five aces	455,798,507	455,798,507	-
Five 3's-5's	1,295,258,323	1,322,503,123	27,244,800
Five 6's-Ks	3,567,135,658	3,539,890,858	(27,244,800)
Straight flush	6,934,852,790	6,920,804,690	(14,048,100)
Four of a kind	107,868,952,548	107,868,952,548	-
Full house	35,263,774,770	35,263,774,770	-
Flush	27,855,203,277	27,796,201,257	(59,002,020)
Straight	93,098,460,163	93,241,750,783	143,290,620
Three of a kind	472,931,297,676	472,889,153,376	(42,144,300)
Nothing	908,473,674,115	908,445,577,915	(28,096,200)
Total	1,661,102,543,100	1,661,102,543,100	-

As you can see, the number of five aces combinations on the draw remained the same. However, some five of a kinds in the range of 6-K moved to 3-5.

However, what I wasn't expecting, and what raises a new question is that the combinations for a Straight Flush, Flush, Straight, Three of a kind, and Nothing also changed. The new combinations have more straights and less of everything else. I speculate there is some straight flush draw that has the same expected value for two different ways to play. However, it isn't a situation like a two pair where the distribution of hands on the draw is the same. If the player had a preference for or against variance, it might influence his play.

Another question is that if this mystery straight flush draw evidently can't produce any five of a kinds, because the total combinations remains the same under both the original and gaffed pays, then why did the gaff affect that draw?

Here is how my effect of incorrect strategy table, from the original post on this topic looks before and after the gaff.

Before gaff:

Game	DW 25-15-9-5-3	DW 25-16-10-4-4
DW 25-15-9-5-3	0.00%	1.03%
DW 25-16-10-4-4	0.92%	0.00%
DW 25-15-9-4-4	0.85%	0.01%
DW 20-12-10-4-4	0.95%	0.05%
DW 25-16-13-4-3	0.83%	0.50%
DWBP 9-4-4	1.84%	1.30%
DWBP 13-4-3	1.65%	1.21%
DWBP 10-4-3	1.46%	1.31%
DBDW 12-4-3	1.77%	1.95%
DBDW 9-4-3	1.83%	2.30%

After gaff:

Game	DW 25-15-9-5-3	DW 25-16-10-4-4
DW 25-15-9-5-3	0.00%	1.03%
DW 25-16-10-4-4	0.93%	0.00%
DW 25-15-9-4-4	0.85%	0.01%
DW 20-12-10-4-4	0.96%	0.05%
DW 25-16-13-4-3	0.83%	0.50%
DWBP 9-4-4	1.82%	1.30%
DWBP 13-4-3	1.63%	1.21%
DWBP 10-4-3	1.44%	1.31%
DBDW 12-4-3	1.73%	1.95%
DBDW 9-4-3	1.78%	2.30%

Hopefully JB will stumble upon this thread. Might also be worthy of a Bob Dancer column.

Could the wild deuces be throwing the totals off? It's tricky to determine the "best" hand that contains one or more wilds.

Quote: DRich

Interesting. I would assume playing FPDW we would be holding the "correct" pair (of two pair) for DBDW half of the time. I also wonder if that is factored into the 1.77% difference.

Glad I'm not the only one who finds this arcane stuff interesting.

FPDW will be holding the "correct" for DBDW pair far more than half the time because much of the time, either pair is correct --- such as 3344, 3355, 4455, 6677, 6688, . . . QQKK

Quote: Ayecarumba

Could the wild deuces be throwing the totals off? It's tricky to determine the "best" hand that contains one or more wilds.

I think it does involve a deuce. My closest guess is a hand like 2-5h-6h-7s-8h. The expected value of keeping the straight is 2 and going for the straight flush is 1.936170. Don't suggest making the suited cards consecutive because makes the straight flush draw the much better play.

Have it choose the lowest pair with aces always being low?

Quote: Wizard

However, what I wasn't expecting, and what raises a new question is that the combinations for a Straight Flush, Flush, Straight, Three of a kind, and Nothing also changed. The new combinations have more straights and less of everything else.

First of all, thanx for suggesting the gaff to JB's program. That same gaff would work on WinPoker, VPW, etc. I hadn't thought of it when I wrote the original post. It's a useful trick to have in one's arsenal.

In FPDW, there is one type of hand where there is a straight flush draw where there's a tie. Using Dancer/Daily notation, it's where you have a 0-deuce SF3-2 with a straight penalty. For example, with '864' K7, it's equal EV whether you hold '864' or 8764. A change in the value of quints doesn't affect the play of this hand.

If you exclude the tie hands and look at the ones that are really, really close, all of them contain the possibility of a royal or wild royal. The frequency of these hands didn't change in Shack's analysis. So it beats me why there are some differences in the frequency of straights if you slightly increase the value of some 5-of-a-kinds.

I'm not taking the time to do it, but I wonder if you'd get the same results by making the same gaff using WinPoker? Dean Zamzow and JB have different programs behind their work and it's possible that the Zamzow version doesn't come up with different frequencies for straights for making this play.

Quote: Wizard

I think it does involve a deuce. My closest guess is a hand like 2-5h-6h-7s-8h. The expected value of keeping the straight is 2 and going for the straight flush is 1.936170. Don't suggest making the suited cards consecutive because makes the straight flush draw the much better play.

Although I don't have a better explanation, this can't be it. Remember the frequency of wild royals didn't change. If you're holding one or more bare deuces, you're going to get some of those.

Quote: BobDancer

In FPDW, there is one type of hand where there is a straight flush draw where there's a tie. Using Dancer/Daily notation, it's where you have a 0-deuce SF3-2 with a straight penalty. For example, with '864' K7, it's equal EV whether you hold '864' or 8764. A change in the value of quints doesn't affect the play of this hand.

You're absolutely right, of course. One can see from JB's hand analyzer that the EV of either going for the straight or straight flush is 0.340426. Somehow I think I stumbled upon this bit of information before years ago but forgot the exact game and hand.

Consider the hands where one "wild" deuce is used as a deuce, both in a straight and straight flush. Is the program accounting for these correctly?